水陆两栖飞机着水冲击仿真分析
2014-06-27,,
,,
(海军工程大学 舰船工程系,武汉 430033)
一般情况下,水陆两栖飞机是在水面起降,而在水上降落时会受到很大的冲击力,这有可能使飞机机体断裂。目前,飞机着水冲击问题的研究主要集中在陆基飞机的水上迫降问题上,通过理论研究、模型试验研究和数值仿真来进行。理论研究在经历几代学者的努力下已经趋于成熟[1-3]。如今,随着计算机技术的飞速发展,加之试验周期长成本高,数值仿真在研究飞机水上着水问题上更具优势和必要性。20世纪以来已有很多学者通过仿真软件对飞机水上降落问题进行了研究[4-6]。目前处理飞机着水问题常用的仿真计算分析软件有LS-DYNA、MSC.Dytran以及Fluent。LS-DYNA诞生比较早,虽然其在处理飞机着水问题上是可行的,但如何运用其处理飞机着水过程中的空气-飞机结构以及空气-水之间的耦合作用还有待探讨[7]。黄勇等[8]分别采用LS-DYNA和MSC.Dytran软件对同-飞机模型进行水上迫降数值仿真,结果表明二者均能对飞机水上迫降这种流固耦合问题进行有效求解,但后者在求解空气-水体两相流与飞机结构的流-固耦合计算时更加稳定,且可以得到耦合界面上的压力分布。Fluent软件主要用来模拟从不可压缩到高度可压缩范围内的复杂流动。对于飞机着水这种高度非线性问题其处理起来比较复杂,并且其对网格质量要求很高,计算耗时较长。文中基于MSC.Dytran仿真平台对某型水陆两栖飞机着水冲击进行模拟,并与模型试验结果进行比对,对水陆两栖飞机着水冲击过载预测数值仿真计算的可行性和有效性进行探讨。
1 算法简介
MSC.Dytran中的流-固耦合方式包括一般耦合和任意拉格朗日-欧拉耦合(ALE),本文采用后者。一般耦合是MSC.Dytran特有的,区别于其他通用软件中的流-固耦合技术,其使流-固耦合模型的建立变得十分容易,且计算速度快精度高。MSC.Dytran有两种求解方法:拉格朗日法求解和欧拉求解法,在分析时间域时采用显式积分法。文中的飞机模型通过拉格朗日法求解,流体模型则通过低阶欧拉求解法。
1.1 拉格朗日求解法
通过显式积分法[9]将运动微分方程
(1)
改写为
(2)
推出加速度
(3)
将单元质量分布在节点上,可以求出节点加速度an
(4)
假设加速度在一个时间步内是恒定的,在时间推进上采用中心差分法。
v(n+1)/2=v(n-1)/2+an(Δt(n+1)/2+Δt(n-1)/2))/2
(5)
dn+1=dn+v(n+1)/2Δt(n+1)/2
(6)
式中:M——结构质量矩阵;
C——结构阻尼矩阵;
K——结构刚度矩阵;

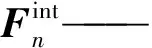

vn——速度;
dn——位移,n=1,2,3,…。
1.2 低阶欧拉求解法
通过将控制方程[10]
质量守恒
(7)
动量守恒
(8)
能量守恒:
(9)
乘以时间积分的时间步可以求得该时间步内的变化量关系。在tn时刻,假定各参数已知,对相邻元素形心处的流速进行线性插值求得元素边界处的流速
ub=(1/2)(u1+u2)
(10)
进而得到单元表面质量、动量和能量的流量
ΔM=ρ2ΔV
(11)
ΔMom=ρ2u2ΔV
(12)
ΔTE=ρ2(et)2ΔV
(13)
式中:(ΔV)i——从时刻tn~tn+1的一个时间步长内流过该单元的第i个表面的体积流量;
ρ2——相邻单元密度。
采用单点高斯积分可得到有关物理量的线性函数,将其代入控制方程可得关于单元形心处各物理量在tn+1时刻的值的线性代数方程组
(14)
(15)
(16)
由上式可以解出tn+1时刻单元形心处的物理量的值。根据材料本构关系计算压力值。
1.3 流-固耦合
拉格朗日网格原本是与欧拉网格完全独立的,欧拉网格不会对拉格朗日网格产生任何影响,而通过耦合算法则可以使两者产生相互作用。一般耦合法中,在拉格朗日结构上建立一封闭耦合面,该面在拉格朗日求解域和欧拉求解域中起传递作用力的作用。欧拉单元内的应力作用在耦合面上,使得拉格朗日单元发生变形。
2 着水冲击分析模型
2.1 全机模型
某型水陆两栖飞机重55 t,着水初始攻角6°,水平速度为42 m/s,下沉速度为2.1 m/s。本文利用MSC.Patran软件按照缩尺比1∶9建立全机有限元模型。水陆两栖飞机模型的壳单元全部采用四边形板壳元(Quad)。其中,为保证计算精度,对水陆两栖飞机船身底部的网格进行加密处理,通过Global edge length将机身底部网格单元大小设为0.03,飞机其他部分网格大小设为0.06,飞机壳单元数为10 741。飞机机体采用刚形体材料以保证机体完整性。初始时刻模型断阶最低点距水面0.15 m。
2.2 流体模型
流体模型包括空气模型和水体模型,其中空气模型是20 m×0 m×1.5 m的六面体;水体模型是20 m×10 m×3 m的六面体。空气和水的欧拉单元均是六面体单元(Hex),为保证计算精度,在空气与水交界处对网格进行加密,同时对撞击区域网格进行加密,加密结果见图1。空气域网格单元数为48 000,水体网格单元数144 000。

图1 流体模型
2.3 空气与水的状态方程
γ律状态方程用于描述空气域的压力
P=(γ-1)ρe
(17)
式中:e——单位质量比内能;
ρ——材料的质量密度;
γ——空气比热比。
水域内的压力用如下状态方程表示
(18)
式中:p——压力;
e——单位质量比内能;
μ——水密度,μ=ρw/ρ0-1,ρw;
ρ0——参考密度;
a1——水的体积弹性模量,a1=2.2 GPa。
水和空气的状态方程中的参数见表1。

表1 水和空气参数
2.4 输出选择
在水陆两栖飞机上共选择3个输出控制点,分别位于飞机首部、中部和尾部,见图2。

图2 输出控制点位置
3 结果与分析
运用Dytran得到的仿真结果见图3。

图3 仿真结果
由图3可见水陆两栖飞机在着水后在水面上作振荡运动,随着飞机向前运动振荡幅度不断减小并趋于平缓,这与该型水陆两栖飞机模型试验现象是一致的。
该型水陆两栖飞机模型试验在某研究所拖曳水池进行。模型以14 m/s的水平速度,0.7 m/s的下沉速度和6°姿态角着水,初始时刻断阶最低点距离水面0.15 m。试验中在模型首、中、尾分别安装加速度传感器,分别测量首、中、尾的垂向过载。
着水过程中机体各处的过载随飞机的运动而不断变化,图4~6分别给出水陆两栖飞机首部、中部和尾部对应的过载试验值与仿真值的对比结果。

图4 首部过载时历曲线

图5 中部过载时历曲线

图6 尾部过载时历曲线
由图4~6可见,水陆两栖飞机在入瞬间飞机所受过载即达到峰值,随后衰减,之后会有小幅波动。
同时也可以看出仿真结果与试验值规律一致,说明仿真可行。仿真峰值相对试验值稍小,且达到峰值后试验得到的过载时历曲线起伏较大且起伏频率较高。这是由于试验时空气密度等因素影响导致机翼产生的升力没有达到0.7g而使试验峰值较大;试验中飞机着水后水压迅速向四周扩散,遇到池壁后发生反射并作用在飞机上而导致过载起伏变化较大且频率较高。试验与仿真结果的峰值见表2。首部受到的过载峰值最大,中部过载峰值与之相当,尾部过载峰值最小,首部和中部的过载峰值均在2g以上。

表2 试验与仿真结果峰值
4 结论
1)水陆两栖飞机入水瞬间飞机首、中、尾过载便达到峰值,其中首部过载峰值最大,中部过载峰值比首部稍小,尾部过载峰值最小,其中首部和中部过载峰值均在2g以上;
2)对相应部位网格加密后得到的仿真结果与试验值基本吻合,规律基本一致,受试验外界条件影响,试验所得过载峰值较仿真结果大;
3)一般耦合算法在处理水陆两栖飞机着水冲击问题上是可行的,并且仿真结果较为准确,可以为试验研究提供预试验分析,可以作为如何布置传感器以及如何选择传感器量程的参考依据,可以在很大程度上提高试验效率,减少试验成本。
4)将飞机材料设为刚体,在后续研究中还可以将飞机材料设为弹性材料或机身局部设为刚体材料进行仿真计算,分析材料选择对仿真结果的影响规律。
[1] von KARMAN. The impact of seaplane floats during landing[R]. NACA TN321,1929.
[2] WAGNER. Trans.phenomena associated with impacts and sliding on liquid surfaces[R]. Math Mech,1932,14:153 68.
[3] MONAGHAN R J. A review of the essentials of impact force theories for seaplanes and suggestions for approximate design formulate[R]. Rep. Mem. 2720,Aeronautics Research Council,London,UK,November 1947(published,1952) .
[4] 贺 谦,李元生,李 磊,等.基于ALE方法的飞机水面降落过程[J].爆炸与冲击,2010,30(2):125-130.
[5] 罗琳胤,杨仕福,吕继航.水陆两栖飞机着水响应模型与数值分析[J].机械设计,2013,30(8):86-89.
[6] 武庆威,高霄鹏,吴 彬.水上飞机滑行阶段静水阻力性能的一种估算方法[J].船海工程,2013(3):154-157.
[7] 黄 勇.民用飞机水上迫降数值模拟计算研究[C]∥第十届全国振动理论及应用学术会议,南京,2011,10.中国振动工程学会,2011:1130-1137.
[8] 黄 勇.民用飞机水上迫降水载荷预测方法研究[C]∥第十届全国振动理论及应用学术会议,南京,2011,10.中国振动工程学会,2011:1138-1147.
[9] 丁沛然,钱 纯.非线性瞬态动力学分析-MSC.Dytran理论及应用[M].北京:科学出版社,2006.
[10] 卞文杰,万 力,吴莘馨.瞬态动力学CAE解决方案MSC.Dytran基础教程[M].北京:北京大学出版社,2004.
