导边形状对轴流式喷泵性能影响的计算分析

，，，

(海军工程大学 动力工程学院，武汉 430033)

喷水推进在高速高性能船舶领域得到广泛应用[1-3]。喷水推进器主要由喷水推进泵(以下称为喷泵)和进水流道两部分构成。喷泵是喷水推进核心部件，喷泵对效率、扬程、流量、抗空化等方面有较高要求，设计难度较大[4-5]。近年来，计算机技术和计算流体力学(computational fluid dynamics，CFD)发展很快，与传统水力模型试验相比，其周期短，耗资较少，CFD在船舶喷水推进技术研发、预报、设计中的应用日趋广泛。在以前叶片进口边位置和形状主要凭经验来设计，对性能曲线的影响只有试验后才知晓[6]。在理论上，通过泵气蚀余量公式，认为修圆叶片进口外圆部分可以提高叶片的抗汽蚀性能[7]。杨军虎等[8]利用CFD软件FLUENT对低转速轴流泵进行过叶片外缘修圆对性能的影响进行过研究，重点对叶顶间隙的流场进行了分析。国外Angelo Cervone、Giovanni Pace等利用水力试验，研究发现导边几何形状对空化特性影响较大。对于高转速轴流式喷水推进泵，空化是非常重要的考虑因素，叶片导边形状对该空化性能和水力性能之间的影响研究报道仍比较少。为了研究导边形状对水力效率和空化性能的影响情况，文中运用CFD方法，通过改变某高速摩托艇喷水推进泵导边形状，研究导边形状对该类喷水推进泵敞水效率和空化性能的影响,为高转速泵的设计、性能优化提供基本参考。

1 控制方程与湍流模型

1.1 控制方程

流体流动须遵守质量守恒规律，动量守恒定律和能量守恒定律。控制方程即为这些守恒定律的数学描述，包括连续性方程和动量方程(也称Navier-Stokes方程，简称N-S方程)。在定常条件下，选用不可压缩的三维连续方程和RANS方程模拟喷水推进泵内流场。

1)质量守恒方程。

▽·(ρV)=0

(1)

2)动量守恒方程(N-S方程)。

(2)

3)能量守恒方程。

(3)

1.2 湍流模型

利用有限体积法对RANS偏微分方程进行离散，进而对其进行数值求解。所有算例都采用SST(shear stress transport)模型来封闭方程组。SST模型结合了κ-ε模型和κ-ω模型的优点, 在近壁面区域，采用κ-ω模型模拟，湍流耗散较小，收敛性好。在湍流充分发展区域，采用κ-ε模型，计算效率高，对复杂流场的适应性更好。两种模型的结合能够较好地模拟粘性底层的流动[9]。SST模型的最大优点就在于考虑了湍流剪切应力，从而不会对涡流黏度造成过度预测[10]。研究采用高阶SST模型。

1.3 CFD方法验证

在对该高速摩托艇轴流式喷泵进行CFD计算前，先以KaMeWa71SⅡ型喷水推进器的混流式喷水推进泵为例对其水动力特性进行数值模拟，并与厂商提供的喷水推进器数据进行比较，以验证所用方法和模型的可信性。

KaMeWa71SII型喷水推进器的混流式喷水推进泵几何模型见图1。

图1 KaMeWa71SII几何模型

该喷泵叶轮进口直管处直径为710 mm，叶轮有6片，导叶11片。该喷泵流体性能数值计算的几何分为喷口、导叶、叶轮以及本文为计算敞水性能所添加的进口直管。喷口和进口直管都用ICEM软件，划分六面体网格。导叶部和叶轮部用TurboGrid软件划分六面体网格，对叶轮进行网格无关性计算，计算结果见图2。

图2 网格无关性计算

经计算叶轮网格至少需要70万，本研究该叶轮网格实取98.3万。其他部件的网格数见表1。

边界条件为总压进口，静压出口。时间步按CFX推荐设置，设为物理时间1/ω(ω为转速，(°)/s)。

喷水推进泵轴功率计算结果见表2。由表2可见，计算值与厂商提供数据相对误差均在1.5%以内，满足工程要求。故从工程应用的角度来看，该方法计算水动力特性是可信的。

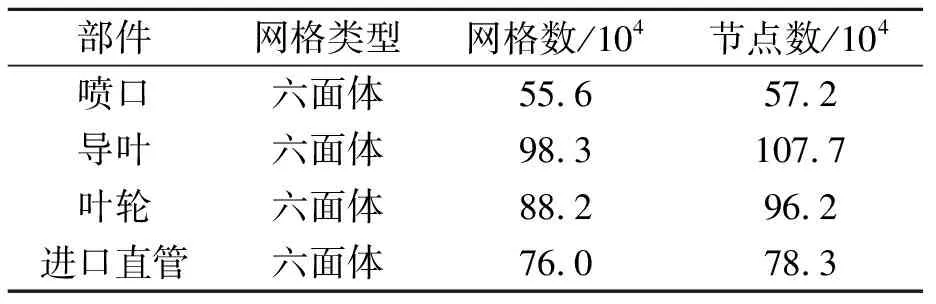
表1 各部分网格数

表2 CFD计算值与试验值对比

2 CFD模拟计算

研究对象为某高速摩托艇喷水推进器的喷水推进泵，其转速较高，额定转速为7 500 r/min。仅以该轴流式泵体的敞水性能为研究对象。该喷水推进泵为单级轴流泵，通过改变导边的修圆情况，研究导边对该泵性能的影响。

2.1 几何建模

根据摩托艇喷水推进器几何，利用CAD三维建模软件UG进行几何建模。喷泵分为叶轮体、导叶体和喷口段3部分。喷泵叶轮叶片为3片，导叶为6片，喷口段也对应设置了6片二级导叶以加强整流效果。该轴流式喷泵尺寸较小，叶轮直径为155.5 mm，叶顶间隙为0.5 mm。导叶体和喷口段几何模型见图3，网格划分见图4。

图3 喷水推进泵几何模型

图4 喷水推进泵网格

对于该喷泵叶轮的建模分为修圆导边几何与未修圆导边的几何。原喷泵几何为叶轮a。叶轮a较未修圆几何叶片(以下称为叶轮c)在导边形状上有较大改变，导边形状为“c”字形。叶轮b修圆程度介于叶轮a、c之间，见图5。

图5 叶轮a、叶轮b、叶轮c单通道几何

2.2 网格划分

叶轮和导叶用ANSYS 12.0软件中专为旋转机械划分网格的CFX-TurboGrid软件。由于叶轮扭曲程度较大，故采用J型拓扑，导叶采用H型拓扑结构。喷口由于包含了二级导叶，几何较为复杂，用ICEM软件，四面体网格进行划分，在壁面边界用菱柱形网格进行加密，对细小部件用密度盒加密，确保对几何描述的准确性。在对叶轮叶片网格无关性分析中，通过对叶轮a单通道网格节点数设定变化，对计算的轴力矩进行监测，力矩变化波动见图6。

图6 网格无关性计算

经计算叶轮总网格至少需70.8万节点，本研究实取80.5万以上。其他部分取较大的网格数以保证网格满足要求。具体网格数和节点数见表3。

表3 具体网格数和节点数

2.3 边界条件设置

对喷泵敞水性能进行计算时，为保证均匀流动，在叶轮进口前加直管进流道，管径与叶轮进口直径相等，长度在2倍直径以上。采用边界条件为流量进口，静压出口边界条件，叶轮叶片与轮毂为相对静止壁面条件，泵壳设为绝对静止壁面条件。在计算空化性能时，在原有基础上加入空化模型进行计算。

3 计算结果分析

喷泵的敞水性能指孤立泵在均匀进流条件下的性能，即不加进水流道的水力性能。模拟计算喷泵在7 500 r/min的情况下，喷泵叶轮分别采用叶轮a、b和c计算流量190～230 kg/s的轴功率、扬程和效率，见图7～9。

图7 轴功率对比

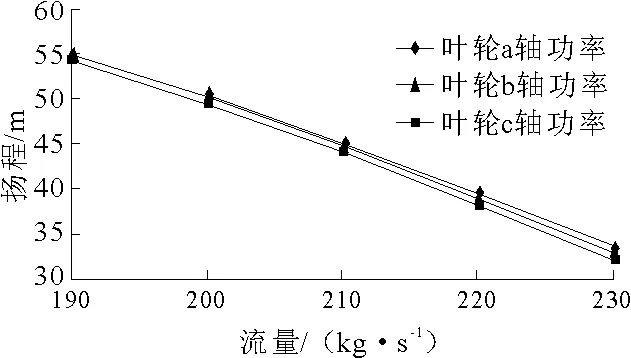
图8 扬程对比

图9 效率对比

分析发现，叶轮a、b和c的功率和扬程都有微小变化。叶轮a的功率最大，叶轮c的功率最小。因为该轴流式喷泵的叶片包角较大，修圆导边后造成叶片做功面积减小，但进流角相对于叶轮c会变大，在这两种作用的综合作用下，造成该泵的功率在叶轮a的情况下所需功率最大。

分析还发现修圆导边对该裸泵的工作点效率影响微小，但在小于工况点的流量时，效率明显低于未修圆导边。分析认为叶轮外缘修圆后，泄漏流动加强，降低了做功效率。

为进一步计算导边形状对空化性能的影响，在原计算模型的基础上加入空化模型，分析叶片在最高效率工况点，流量为210 kg/s时的空化情况见图10。

图10 空化对比

从空化的对比图中可以发现，叶片空化都发生在叶稍和导边部分，叶轮c的空化面积明显最多，叶轮a空化面积最小，这与用理论分析的情况一致。一方面，流进叶轮的液体先与导边中部接触，获得能量后一部分液体沿着导边向叶稍方向流动，旋转能量增加了，压力也增加了，延迟了空化的发生；另一方面通过后处理叶轮的流场矢量，可以发现在叶稍处流动非常剧烈，叶轮a的弧形导边相对于叶轮c的直线导边可以明显地减少来流的冲击，削弱了二次流的影响，见图11。

图11 叶轮流场矢量

叶顶部分是做功和流动最强烈的地方，叶片外缘导边部分修圆以后，造成叶片叶稍卸载，减小了空化发生面积。

4 结论

1)对于高转速的轴流泵，修圆导边的叶片对轴流泵的功率和扬程有微小的影响，会造成小于工作点流量时的效率降低；

2)修圆导边的叶片在空化性能上优于直导边的叶片，空化面积明显减少，有利于叶片叶稍卸载。

[1] BULTEN N.Numerical analysis of a waterjet propulsion system[D]. Eindhoven, The Netherlans:The Eindhoven University of Technology,2006.

[2] 刘承江,王永生,丁江明等.现代喷水推进装置的演变[J].舰船科学技术，2006,28(4):8-12.

[3] ALLISON J L.Marine waterjet propulsion[J].Transaction of SNAME,1993,101:275-335.

[4] ALLISON J L,JIANG C B.Modern tools for waterjet pump design and recent advances in the field[C]∥Internationa Conference on Waterjet Propulsion Ⅱ.RINA,Amsterdam,1998:128-142.

[5] 汤方平.喷水推进轴流泵设计及紊流数值分析[D].上海：上海交通大学，2006.

[6] 李世煌.叶片泵的非设计工况及其优化设计[M].北京：机械工业出版社，2006.

[7] 关醒凡.轴流泵和斜流泵[M].北京：中国宇航出版社，2009.

[8] 杨军虎，马静先，张人会,等.轴流泵叶片外缘修圆对泵性能的影响[J].兰州理工大学学报，2007,33(5):60-63.

[9] 靳栓宝.基于CFD喷水推进泵性能分析及优化设计[J].船海工程，2010，39(2)：125-129.

[10] 谢龙汉，赵新宇，张炯明.ANSYS CFX流体分析及仿真[M].北京：电子工业出版社，2012.