围壁补强的圆柱壳开孔结构有限元分析
2014-06-27,,,
,,,
(中国舰船研究设计中心,武汉 430064)
为了满足各种工艺和结构上的要求,不可避免地要在潜艇耐压壳上开设不同尺度的圆形孔。开孔会破坏耐压壳的连续性,削弱结构的强度,并在开孔处产生很高的局部应力。为了保证潜艇的安全,必须充分考虑开孔加强的问题。目前潜艇耐压壳常用的补强形式有围壁补强和围壁、加厚板联合补强,本文研究围壁补强结构。
1 开孔应力的有限元分析
1.1 计算模型
围壁加强的圆形开孔圆柱壳安装肋骨后,肋骨对孔口区域壳板和加强围壁的应力状态无实质性影响[1]。因此本文采用的计算模型参考文献[2]中计算模型,模型泊松比为υ=0.3,弹性模量E=2.01×105MPa,不考虑材料非线性。圆柱壳半径R=3 500 mm,圆柱壳厚度t=28 mm,围壁与圆柱壳厚度比δ/t=0.5~3.1,开孔率a/R=0.1~0.5,围壁高度H=1 000~3 000 mm,壳体外围壁高度与H比值η=C/H=0.1~1.0。见图1。
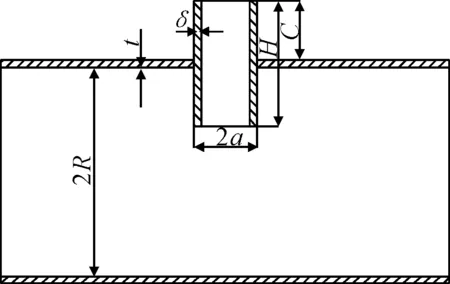
图1 围壁补强的圆柱壳开孔结构示意
围壁和圆柱壳全部采用6面体20节点完全积分单元。由于结构和载荷关于过孔心的横剖面和纵剖面对称,计算模型取结构的1/4,对称面上施加对称边界条件。为了更好模拟耐压壳的真实情况,围壁上端开孔用板密封,结构外表面作用压力p=3 MPa,圆柱壳端部作用施加均布载荷,考虑到孔口周围应力变化大,划分网格时在2倍直径范围内划分出一个区域,对该区域网格进行密化,该区域外的网格稀疏,见图2。

图2 有限元网格
围壁端部40等分,沿壳体和围壁厚度方向划分为两层单元,密化区域其它边界上设定网格种子数为30,SPACE设定为0.5,即越靠近相贯线种子越密集。共计15 060个单元。
p(R+t)2/[(R+t)2-R2]p(R+t)2/
[(R+t)2-R2]
(1)
1.2 等效原理
应力分类方法很多,工程界常用的方法有3种:弹性补偿法、等效原理和应力线性化原理。这3种方法在精度上都可满足工程需要,但弹性补偿法未考虑峰值应力的分类,而应力线性化原理是ANSYS软件中特有的功能,等效原理在经济性和实用性上都是最佳[3],因此采用等效原理对应力分离。
图3为系列模型中某一模型的计算结果应力云图,其它模型应力分布规律和该模型一致。由图3可见,孔口壳板最大应力为过孔心之母线上孔边的周向应力,因此应力分离路径如图4所示。

图3 计算结果应力云图
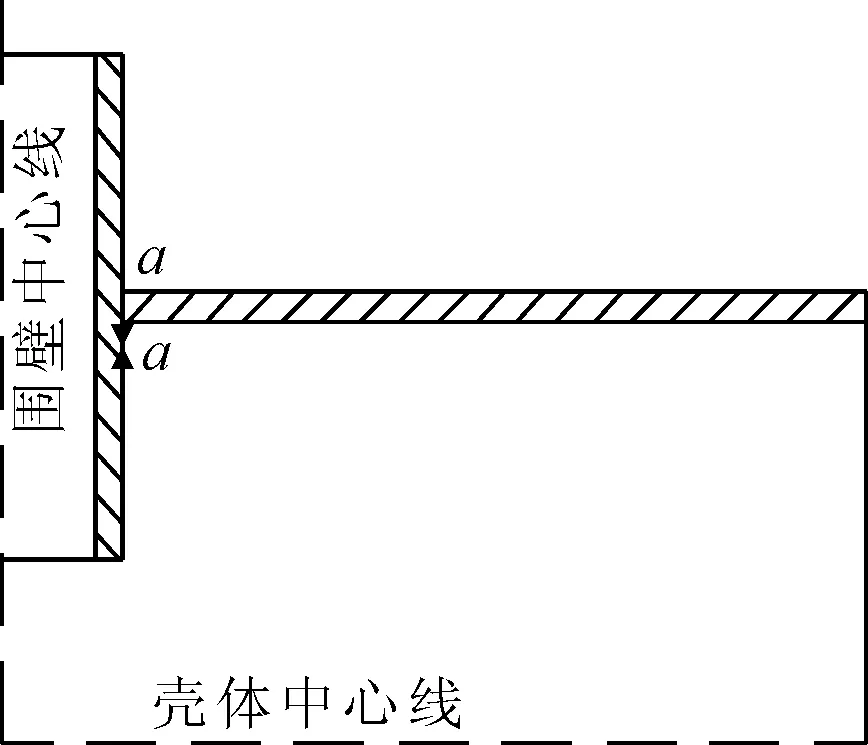
图4 应力分离路径示意
以径向应力σx为例介绍等效原理基本理论。
设应力沿应力分离路径上的分布为二次函数:
σx=C1S2+C2S+C3
(2)
式中:S——路径量纲-的量坐标,取值范围为0~1。
按静力等效原理,沿应力处理线上的均布应力为
(3)
设沿处理线上的弯曲应力为
σb=AS+B
(4)
按静力矩等效原理,有
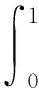

(5)

(6)
解方程组得
(7)
处理线上峰值应力为
σp=σx-σm-σb
(8)
2 a/R和δ/t对各应力成分的影响
为研究a/R和δ/t对各应力成分影响的规律,利用ABAQUS计算H=2 000 mm,η=0.5,a/R=0.1~0.5,δ/t=0.5~3.1,共70个系列模型。计算结果见图5~10,图中符号说明如下:
σm-薄膜应力;σb-弯曲应力;σp-外表面峰值应力;a/R-开孔半径/壳体半径;δ/t-围壁厚度/壳体厚度。
注:以上应力均为应力分离路径上分离出的应力。
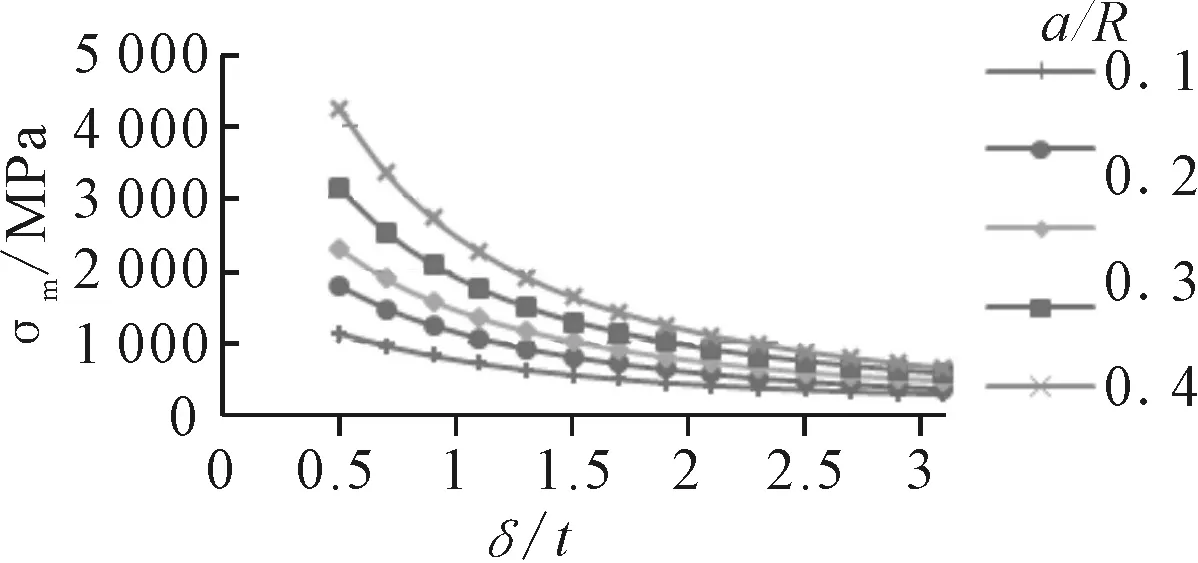
图5 δ/t对薄膜应力的影响
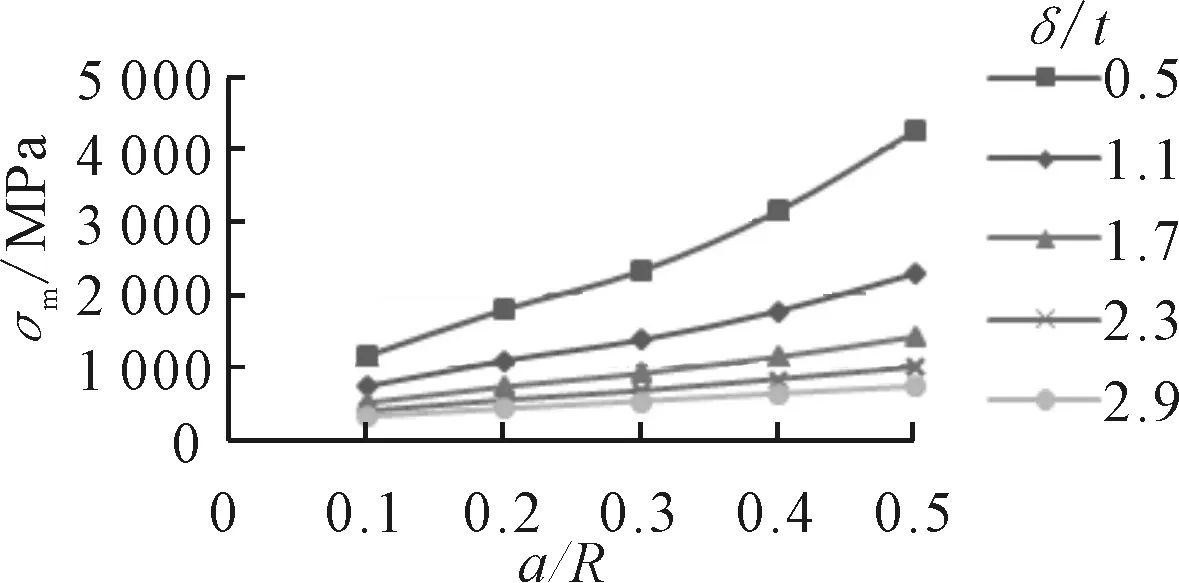
图6 a/R对薄膜应力的影响
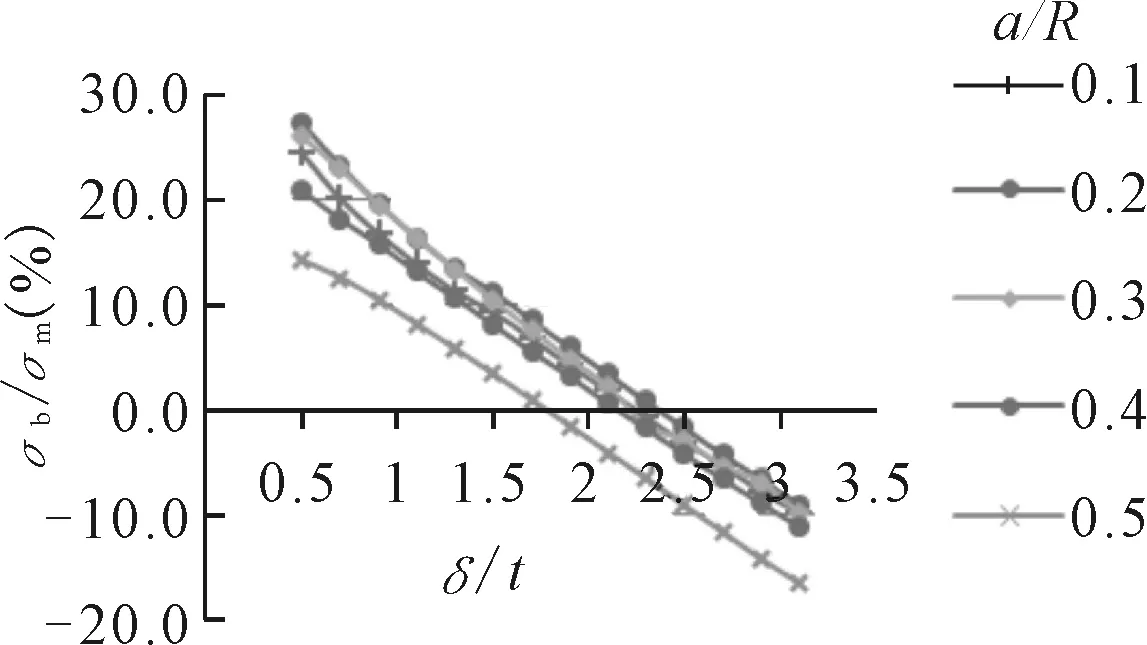
图7 δ/t对σb/σm的影响
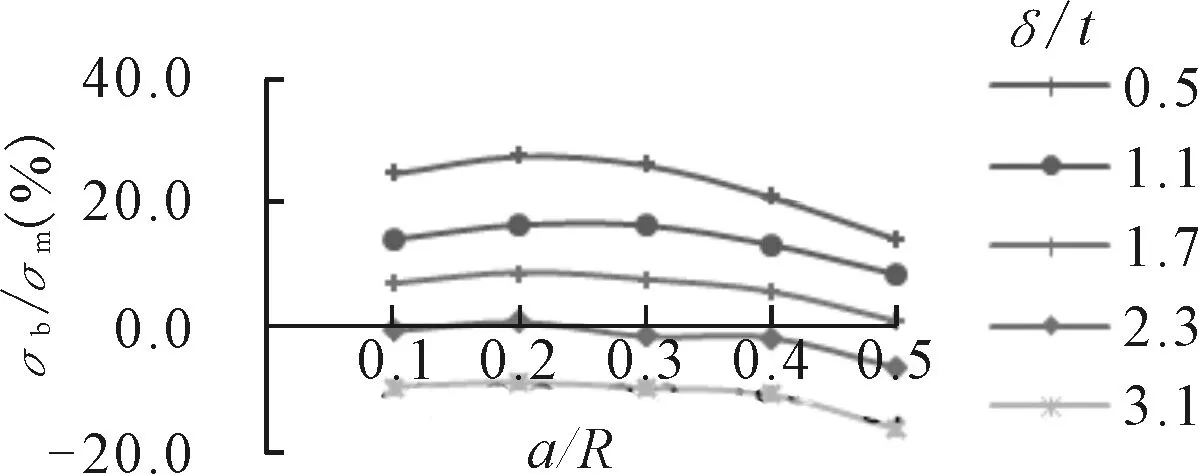
图8 a/R对σb/σm的影响
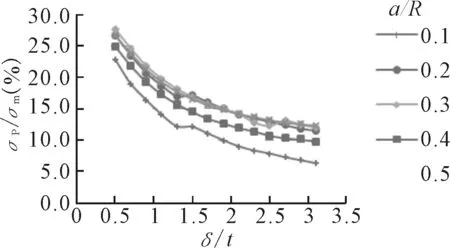
图9 δ/t对σp/σm 的影响
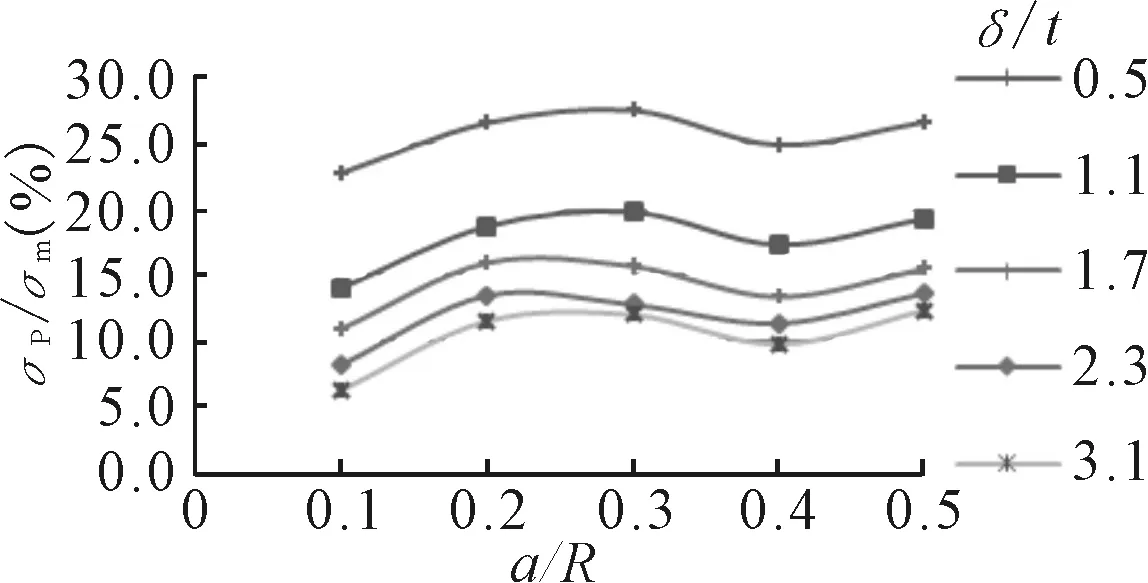
图10 a/R对σp/σm的影响
由图5、6可见,当厚度比δ/t较小时,薄膜应力会很大,且随着厚度比δ/t的增大而急剧降低;当δ/t>2.0时,薄膜应力仍会随着厚度的增大有所降低,但降低趋势较为缓慢。对于开孔率而言,薄膜应力会随着开孔率的增大而增大且厚度比较小时,增加趋势很快,厚度比较大时,增加趋势缓慢。
由图7、8可见,弯曲应力与薄膜应力比值会随厚度比的增加迅速降低,δ/t在2.0附近时降到最低,这时再增加厚度比,弯曲应力反而会反方向增大。随着开孔率的增大,弯曲应力也会增加,但弯曲应力所占比值变化不大。
由图9、10可见,峰值应力与薄膜应力的比值会随着厚度比的增加逐步降低。随着开孔率的增大峰值应力也会迅速增大,但峰值应力所占比值变化趋势不明显。
3 η对各应力成分的影响
该部分研究内容是在开孔率a/R=0.3、厚度比δ/t=1.5、围壁高度H=2 000 mm的前提下进行的,壳体外围壁高度与H比值η对各应力成分的影响见图11、12、13。

图11 η对薄膜应力的影响

图12 η对弯曲应力的影响
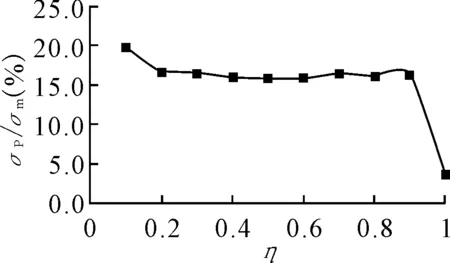
图13 η对峰值应力的影响
由图11、12、13可知,η在0.2~0.9范围内,对薄膜应力、峰值应力几乎无影响,但随着围壁在壳体外的长度的增加,弯曲应力会随之增大。当η<0.2时,由于围壁外伸长度过小,围壁受静水压力作用的面积较小,各应力成分都有所降低,但峰值应力所占比值反而增大。当围壁完全伸出壳体时,这时补强强度急剧下降,薄膜应力和弯曲应力急剧增大,但这时峰值应力反而急剧减小。
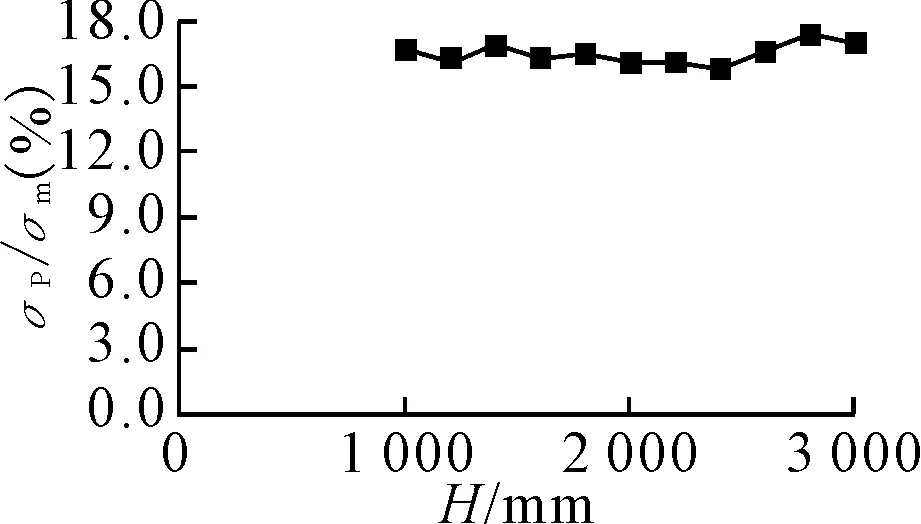
4 H对各应力成分的影响
该部分计算模型参数如下。
a/R=0.3;δ/t=1.5;η=0.5;
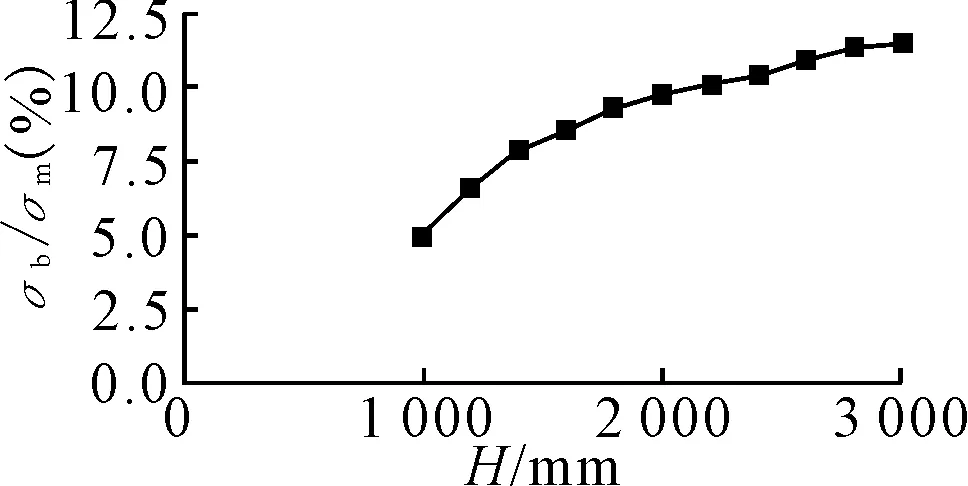
1 000 mm 计算结果见图14、15、16。 图14 H对薄膜应力的影响 图15 H对弯曲应力的影响 图16 H对峰值应力的影响 由图14、15、16可知,围壁高度对薄膜应力、峰值应力几乎没有影响,而弯曲应力会随围壁高度的增加逐步上升,当围壁高度大于2 000 mm时,弯曲应力与薄膜应力比值超过10%,这时弯曲应力不应忽略不计。 1)当圆柱壳的半径和厚度确定时,围壁厚度和开孔半径对补强强度贡献较大,而围壁在壳体外的高度与围壁高度比值以及围壁高度对补强强度贡献较小。 2)围壁厚度的增大能有效地降低薄膜应力,但不应为了降低薄膜应力盲目增加围壁厚度,因 为围壁厚度增大到一定程度后,再增加围壁厚度薄膜应力降低幅度不大,反而会引起弯曲应力的急剧增大。 3)增大围壁在壳体外的高度,对薄膜应力和峰值应力几乎无影响,但会引起弯曲应力的增加。 4)当围壁下端与壳体相接时,此时补强强度最小,薄膜应力和弯曲应力都会急剧增大,因此,潜艇设计时应尽量避免这种情况。 [1] 徐秉汉,裴俊厚,朱邦俊.壳体开孔的理论与实验[M].北京:国防工业出版社,1987. [2] 舒 斌.潜艇大开孔补强结构研究[D].武汉:中国舰船研究设计中心,2011. [3] 龚曙光,谢桂兰.压力容器分析设计中的应力分类方法[J].化工装备技术,2000,21(3):27-31.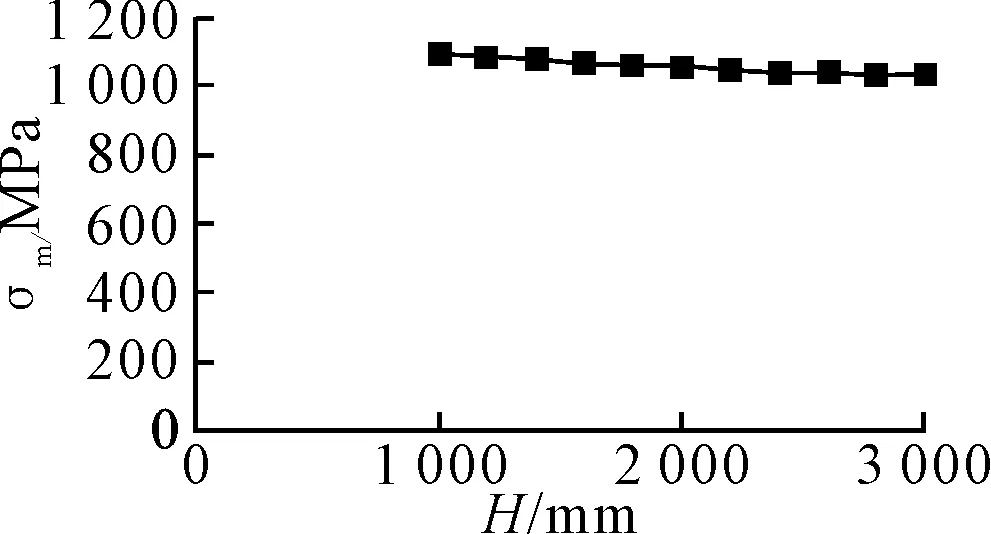
5 结论
