浅析Q轴主电抗增磁降速时对矢量控制系统的影响

2014-06-26刘翔曹萍邸净宇李庆元王希宇张蔚航

电气传动 2014年4期

刘翔，曹萍，邸净宇，李庆元，王希宇，张蔚航

（1.天津电气传动设计研究所有限公司，天津 300180；2.河北工业大学电气工程学院，天津 300130；3.北京航空航天大学仪器科学与光电工程学院，北京 100191）

交-交变频矢量控制系统在我国中压大型传动方面得到了广泛的应用。系统调试需要输入电机的相关参数，对于同步电动机，有时需要改变电机Q轴主电抗参数，才能使电机满足动态性能。本文将利用仿真模型，结合现场调试中出现的实际问题，探讨Q轴主电抗值对系统运行的影响。

1 大功率交-交变频调速系统

大功率交-交变频器通常采用三相桥式晶闸管可逆整流装置。如果触发移相控制信号是直流信号，变频器的输出电压是直流；若触发移相控制信号是交流信号，相应变频器的输出电压则是交流，实现变频。由于这种变频器无中间直流环节，故称为交-交直接变频。通过建模仿真，交-交变频器单相输出仿真如图1所示。

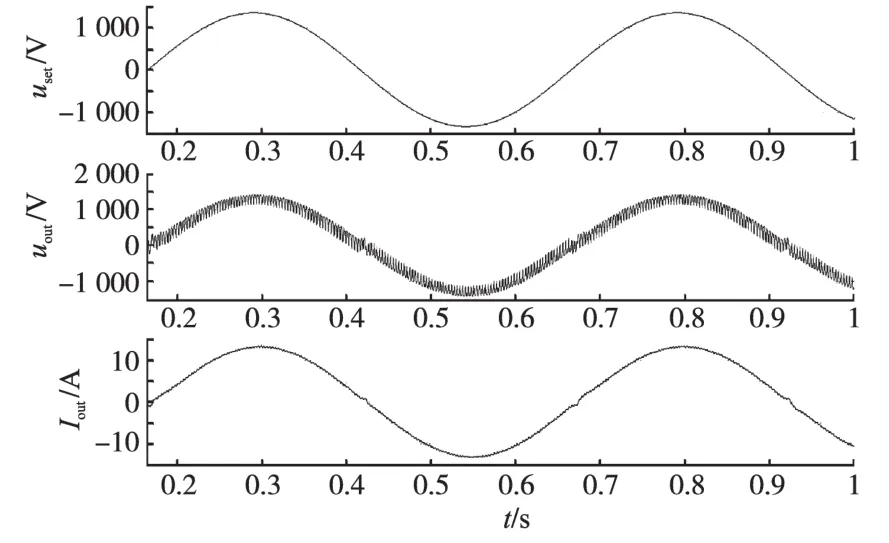
图1 交-交变频器单相输出Fig.1 The phase voltage of AC-AC convertor

同步电动机的动态数学模型是一个高阶、非线性、强耦合的多变量系统。如果以产生同样的旋转磁动势为准则，在三相坐标系上的定子交流电流与电压通过3/2变化可以等效成两相静止坐标系上的交流电流与电压。若观察者站在铁心上与坐标系一起旋转，看到的便是1台直流电机。

既然同步电动机经过坐标变换可以等效成直流电动机，那么，模仿直流电动机的控制策略，得到直流电动机的控制量，经过相应的坐标反变换，就能够控制交流电动机。这样通过坐标变换实现的控制系统叫作矢量控制系统。

20世纪90年代，西门子公司推出了SIMA⁃DYN-D交-交变频矢量控制系统。以其强大的控制性能，与现场应用的可靠性，在我国大型冶金项目中得到了广泛应用。SIMADYN-D是一种基于总线结构的多处理器通用控制器，硬件有多种机箱、处理器模版、通信缓冲模版、接口模版、部通信模版等模块以供不同的任务选择，组合使用。

2 系统仿真模型

同步电动机矢量控制系统框图如图2所示。

以系统框图为基础，结合实际系统原理，搭建仿真模型如图3所示。

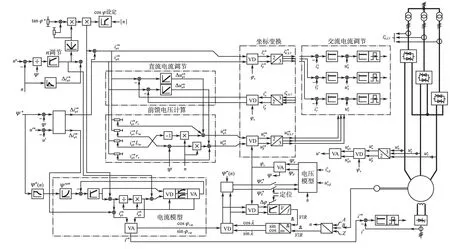
图2 同步电动机矢量控制系统框图Fig.2 Block diagram of the synchronous motor vector control system

图3 同步电动机矢量控制系统仿真模型Fig.3 The simulation model of the synchronous motor vector control system

本文中讨论的Q轴主电抗值主要对电流模型产生影响，图4为电流模型的封装包。其内部结构如图5所示。

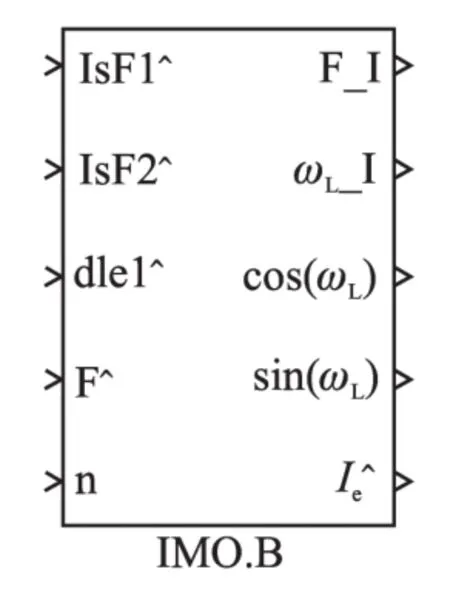
图4 电流模型Fig.4 Current model

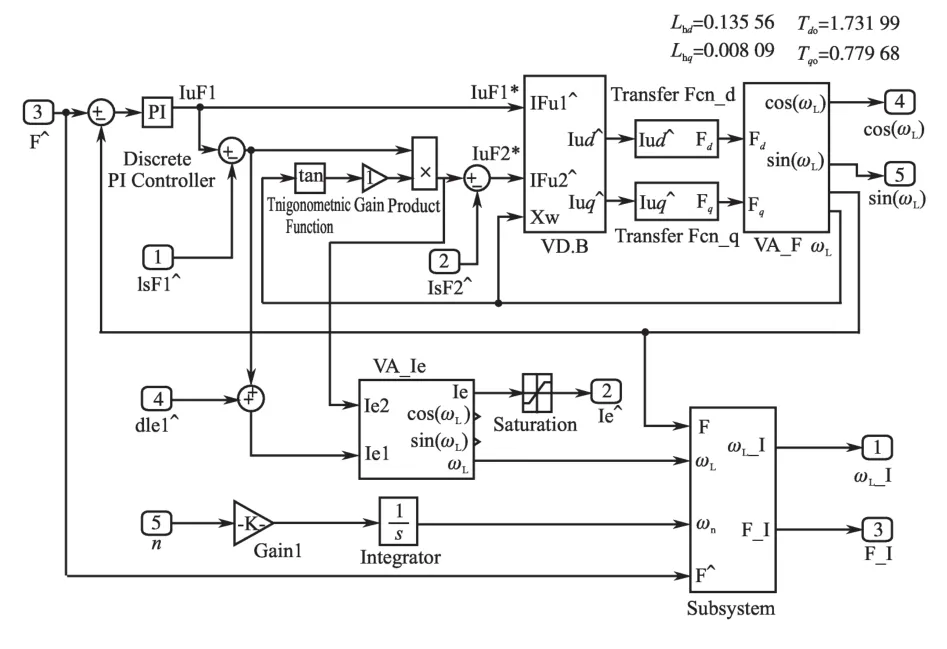
图5 电流模型内部结构Fig.5 The internal structure of current model

电流模型为系统提供励磁电流的给定值，同时由于系统在低速阶段运行时，电压模型的误差较大，因此，在低速运行阶段，电流模型为系统提供控制所需的磁链值。

3 实际中遇到的问题与分析

3.1 问题

在某现场调试时，对电机做往复升降速实验，多次在增磁降速时，系统失稳，最终导致跳闸自由停车。现场调试过程中实际波形如图6所示。

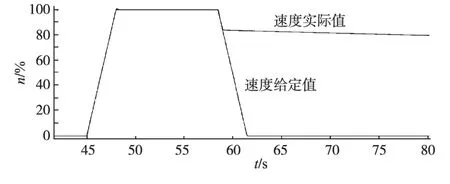
图6 速度波形Fig.6 Speed waveforms figure

同时，在增磁降速过程中，监控电机其他参数，发现有所异常。

图7为状态异常时波形，由图7可以看出，当电机进入增磁降速段时，本应该增磁的磁通没有增加，反而在下降；在系统封锁前，转矩电流在正负50%之间反复变化；转子附加电流达到限幅，进入饱和区，定子附加电流也接近限幅。

从表1可以看出，攀枝花典型钛精矿粒度中，-60～+100目的钛精矿比例不足30%，这主要是由于攀枝花钒钛磁铁矿特性和钛精矿选矿布局、工艺等原因，导致钛精矿粒度偏细，不能用作盐酸浸出法来制备合格的沸腾氯化原料。并且存在钛精矿粒度越来越细化的趋势，可用于生产人造金红石的钛精矿比例逐步下降。

图7 状态异常时的波形Fig.7 Waveforms figure in abnormal state

图8为状态正常时波形，由图8可以看出，电压与力矩电流波形在开始降速一瞬间会有一些波动，之后随着系统的调节趋于平稳；磁通随着转速的下降开始增大；转子与定子的附加给定调节量大致在正负15%之间，波动大幅度减小。

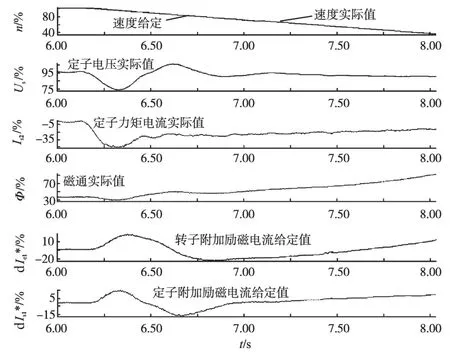
图8 状态正常时的波形Fig.8 Waveforms figure in normal state

3.2 分析

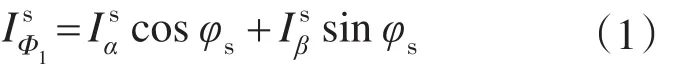
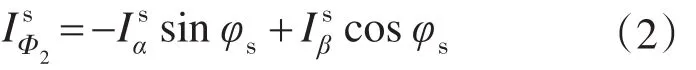
式中：φs为磁链与α轴夹角，等于转子位置角λ与负载角φL之和。

由图7中可以看出定子力矩电流在正负50%之间波动，而正常制动电流值不会在短时间内有如此大的波动，从而判断形成这样波形的原因应该是由φs的计算误差造成。φs为转子位置角λ与负载角φL之和，λ由编码器及编码器模块得到，在编码器正常的情况下，λ的值也是准确的。误差是在计算φL时产生的。

φL可以由电压模型和电流模型计算得出，在电机运行与高速段时，φs由电压模型提供。此时电流模型计算出的φL仅用于励磁电流给定Ie*的计算，并且此时的电流模型只为系统提供Ie*，计算出的其他量皆不对系统产生影响。现场调试过程中，认为电机厂提供的参数与真实参数存在误差，参考其他电机参数与以往调试经验，将电流模型中Q轴主电抗参数Lmq减小到60%后，系统运行正常，实验得以顺利通过。

Lmq在电流模型中，被用于图5的TransferF⁃cn_q功能块中，Q轴磁链Ψq的计算为

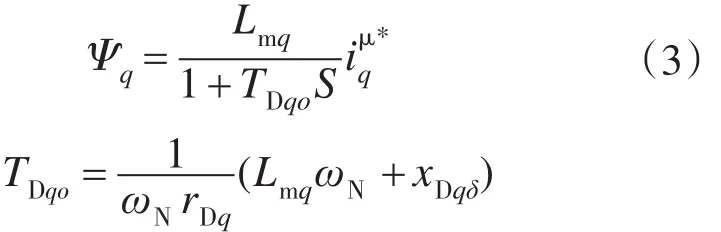
图9 不同Q轴电抗值时的负载角波形Fig.9 Load angle waveforms in different Q⁃axis reactance value

图10 不同Q轴电抗值时的励磁电流波形Fig.10 Excitation current waveforms in different Q⁃axis reactance value

从图9中可以看出，在修改Q轴主电抗值后，计算所得到的负载角要比修改前的φL小。磁化电流iμ由定子电流is，励磁电流ie共同产生，其在Φ1轴上的分量为电机运行提供所需磁链的给定值由磁链调节计算得出：

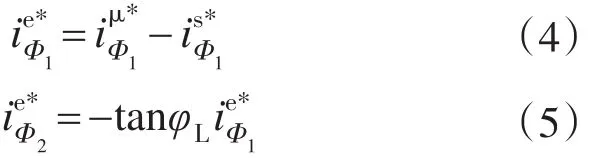
图11 增磁降速时向量图Fig.11 The vector diagram when increasing the magnetic and slowing down the speed

从图11中明显看出，当负载角φL计算错误时，励磁电流Ie增大许多，而用于产生磁链的却在减小。这样就解释了为何励磁电流在增大，而图7中的磁通却在减小。同时，由于此时电机欠磁运行，为了满足转矩的需要，迫使定子产生更大的转矩电流，从图8可以看出，正常时转矩电流稳定在30%左右，而图7中的转矩电流在50%附近。

定子附加给定是由电压给定与实际电压的差值ΔUs经过比例环节得到，而转子附加给定是由ΔUs经过比例积分环节得到，也就是说，其大小由ΔUs决定。

在速度一定的情况下es同磁通成正比，由上文可知，在Q轴主电抗取值不准确时，产生的磁通要比实际所需的小，因此es也会相应变小，从而ΔUs增大，导致定转子附加给定过大。由图8可以看出，在实际调试中，将电抗减小后，定转子附加给定最大峰值只有15%左右，相比未改动前，系统稳定运行，说明调整后的参数更接近正确参数。

输入错误的Q轴主电抗值，系统出现异常多发生在增磁降速的区域，而弱磁升速过程往往得以顺利通过。这主要是因为同步电机中的阻尼绕组造成的。

在弱磁加速过程中，阻尼绕组一方面使定子转矩电流响应加快；另一方面阻碍了气隙磁链的变化。从而，阻尼绕组对磁链减弱的阻碍作用反而增大了加速转矩，有利于电机的加速特性。

但在增磁降速过程中，阻尼绕组同样又会阻碍磁链的增加，使得本身因为Q轴主电抗不准而造成的欠磁雪上加霜。由于欠磁，使得产生的转矩不足，负载角不断加大，最终导致失步，系统封锁。