考虑铁损电阻变化的风电感应电机节能优化

吴帆，王鹏，韩正之

（上海交通大学电子信息与电气工程学院，上海200240）

1 引言

电机系统节能工程被列为我国“十二五”10大重点节能工程之一。如何进一步提高风力发电机组的效率是新能源风力发电领域的一个非常重要的问题。由于风场的风速具有波动和不确定性，机组可能长期在轻载模式下运行，因此考虑额定风速（一般为12 m/s）以下的机组运行效率十分必要。

目前，感应电机运行效率的提高多通过改变电机运行时的磁链幅值大小来实现，其幅值的确定可以归纳为搜索法和损耗模型法两种［1］。搜索法是通过搜索电机运行的最小电流或最小输入功率来确定最优运行点，不依赖于电机参数和模型，但是对电流、功率、转速等的测量要求高，算法收敛时间长，且可能发生抖动［2-4］。损耗模型法是通过建立异步电机损耗模型，根据当前负载和速度大小，实时算出最优励磁的数学方法。计算过程简明快捷，控制效果平滑，转矩波动小，收敛性好。鉴于风电系统在风速变化过程中对系统动态性能要求高，采用损耗模型法更适于实际应用推广。但损耗模型法需要精确建模，模型的精确与否受电机参数和环境温度的变化影响。采用模型计算，存在模型不准确带来的状态误差，会影响系统最优点求解。因此，基于损耗模型对感应电机进行最优控制，关键在于模型的准确程度。

本文研究的鼠笼型全功率风力发电机的效率优化问题，将从分析电机模型入手，建立变铁损电阻的电机模型和考虑变铁损电阻的损耗模型，然后通过这个精确的损耗模型求取最优磁链。最后通过仿真验证，证明该方法节能效果更好。

2 考虑铁损的电机模型

异步电机在运行过程中主要包括以下几个方面的损耗：

1）定转子绕组中电流通过产生的铜损；

2）定转子铁芯中磁场产生的铁损（包括磁滞损耗和涡流损耗）；

3）气隙磁场高次谐波产生的杂散损耗（杂散铁损和杂散铜损）；

4）由于风扇和轴承转动所引起的机械损耗。

杂散铁损是气隙的谐波磁链相对定转子铁芯表面发生移动而产生的损耗，以及由于定转子间齿槽的相对移动、磁阻的变化使得齿内磁链脉动而在齿中产生的损耗之和；杂散铜损是齿槽漏磁链引起导体中电流的集肤效应导致等效电阻增加产生的损耗［5］。杂散损耗建模困难，且不能通过弱磁来控制。而机械损耗又是由生产工艺技术和设备运行工况而定的，与电气变量无关，因而他们都属于不可控损耗。定转子铜损和铁损属于可控损耗，约占总损耗的80%。因而在研究节能控制时，一般只考虑可控损耗。

本文采用在同步旋转d-q坐标系下建立的电机模型［6-8］。考虑铁芯损耗的异步电机等效电路如图1所示。

图1 电机等效电路Fig.1 Equivalent circuit of IG

模型中使用与励磁电感Lm并联的铁损电阻RFe代替电机运行时产生的铁芯损耗。用以模拟铁损的电阻是从标准的空载实验得来的。通过电机等效电路图，采用模不变的坐标变换，可得到发电机的数学模型：

磁链方程为

电压方程为

电流方程为

转矩方程为

式中：V，i，Ψ分别为电压、电流和磁链；Lσ为漏感；下标m表示参数或变量与主磁通有关；下标Fe为与铁芯损耗有关的量；下标s和r分别为定子和转子；Te为电磁转矩，np为发电机极对数；ωa为同步角速度，即定子的电角速度。

3 优化方法

变流器通常采用按转子磁链定向的矢量控制方法，把d-q坐标系放在同步旋转磁场上，从而静止坐标系中的各个交流量被转化为旋转坐标系的直流量。此时有：

式中：ωs表示转差角频率。

应用文献［9］的方法，分析系统稳态时的损耗情况，将式（5）代入电机数学模型式（1）～式（4），得到：

若忽略磁路饱和与温升对电机参数的影响，发电机损耗Ploss可按文献［10］计算如下：

定子铜损是定子回路部分的铜耗之和，即

转子铜损是转子回路部分铜耗之和，有

铁损可以根据励磁回路里用以表示铁损的电阻RFe消耗的功率求得，即

总可控损耗是以上3 种损耗之和。将式（6）中的各个电流代入式（7）～式（9）中，求和得到总损耗如下式所示：

其中

由于铁损电阻RFe的阻值不是常数，而是一个随着同步旋转磁场的频率不断变化的量。控制中又用到了RFe进行转子磁链定向，因此，铁损电阻的准确性对于转子磁链的准确定向尤为重要。文献［11］中的数值结果也表明了铁损电阻的实际值和给定空载实验所得值之间的差异，会引起定向角的误差。本文中采用下式变化关系得到铁损电阻：

式中：RFe50为给定的工频空载实验测得值；f 为定子频率。

根据上述分析可知，在电机参数不变，给定转矩和转速的情况下，电机的可控损耗PLoss是转子磁链Ψr的凹函数。为了进一步分析转子磁链与电机可控损耗间的关系规律，在Matlab 上对PLoss进行数值分析计算，可以得到可控损耗PLoss与Ψr间的关系如图2所示。

图2 损耗—磁链曲线Fig.2 Power loss-flux curve

从图2 所示曲线可以看出，在不同的转子磁链条件下，可控损耗先单调递减再单调递增，存在一个最低点，也就是说通过适当调节磁链大小可以使得可控损耗达到最小。这样，研究电机效率优化控制方法的关键就在于找到一个最优的磁链值使得可控损耗达到最小。通过对损耗求导可以得到这个最优磁链：

4 仿真及试验验证

为了检验上述方法的正确性，在一台350 kW鼠笼型异步风力发电机的基础上进行了系统分析与仿真验证。

4.1 系统参数

系统的拓扑结构如图3所示。

图3 系统拓扑结构Fig.3 Topology structure of system

系统由鼠笼型感应发电机（SCIG）、PWM 变换器构成，直流环节用直流电源Udc代替。350 kW发电机参数如下：额定功率PN＝350 kW，额定定子频率f＝50 Hz，额定转速nG=1 000 r/min，额定转矩TeN=3 342.5 N·m，定子电阻Rs=0.017 9 Ω，转子电阻Rr=0.023 3 Ω，定 子 漏 感Lσs=转 子 漏 感Lσr=0.028 9 mH，互感Lm=12.414 mH，额定时铁损电阻RFe50=48.54 Ω，转动惯量J=30 kg·m2，极对数np=3。

本文提出的优化方法是通过改变发电机给定磁链来实现的，这里给出变换器对感应发电机的控制框图，如图4所示。

图4 控制系统框图Fig.4 The block diagram of control system

采用转子磁链定向的矢量控制方法［12-14］，实现磁链与转矩的解耦控制。其中，转速调节ASR得到转矩电流的给定值isq*，而励磁电流的给定值isd*是通过上文提出的损耗模型获取的磁链的最优点计算得到，其输入是转矩Te和转速ωr。

4.2 模型计算

最大功率跟踪情况下，6个典型工作点如表1所示。

表1 电机典型工作点Tab.1 Typical operating point of IG

通过式（11）可以求得6组固定转速和转矩下的铁损电阻值，通过3 阶曲线拟合可以得到铁损电阻与转速［12］的关系曲线如图5所示。

不同转速对应的最佳磁链可以通过对损耗求导得到最优（对应最小损耗）磁链值，通过3 阶曲线拟合可以得到给定磁链与速度的关系如图6所示。

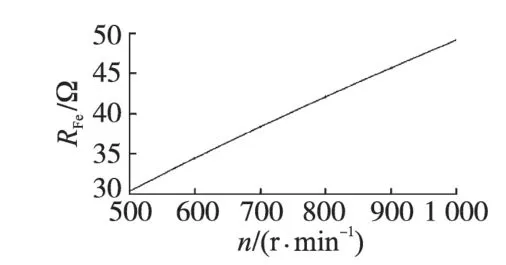
图5 RFe特性曲线Fig.5 Characteristics curve of RFe

图6 磁链拟合曲线Fig.6 Fitting curve of flux

4.3 仿真结果

下面将利用Matlab 的Simulink 工具箱对上文的电机损耗模型进行仿真［15］，并用其算得的最优磁链对电机进行按转子磁链定向的矢量控制。

仿真电机使用变铁损电阻电机模型，采样周期Ts=2e-6 s，0 s启动电机，负载转矩506 N·m，给定转速500 r/min。前4 s 采用额定磁链控制，4 s时刻切到最优磁链控制，即采用前面得到的在转矩转速给定时的最优磁链值。

给定磁链切换过程和实际磁链的跟踪过程分别如图7、图8所示。

图7 给定磁链切换过程Fig.7 Switch process of given flux

图8 实际磁链变化Fig.8 Variation of real flux

在磁链给定切换下，定子电流［7］ids，iqs在3～7 s时间内变化曲线如图9所示。

图9 定子电流变化曲线Fig.9 Curves of stator current variation

从图9 可以看出，励磁电流ids和转矩电流iqs都可以实现快速跟踪，并且ids能够在磁链切换瞬间完成切换，而iqs的变化是需要一个过程的，从图4 可以看出iqs是通过Ψr计算得到的，Ψr稳定时间取决于转子时间常数Tr。

直流侧的输出功率在3～7 s 时间内变化过程如图10所示，负值表示发出功率。

图10 输出功率变化曲线Fig.10 Curve of output power

由仿真结果可以看出，最优磁链控制时的输出功率约为23 000 W，额定磁链控制时约为20 500 W。由此可以得到节约功率约为2 500 W，节约12.2%。

将不同转速下最优磁链与额定工作点的给定磁链控制下得到的损耗值比较，在全速度范围内损耗对比如图11所示。

图11 损耗对比曲线Fig.11 Comparison curves of power loss

图11 中曲线1 是所有转速下都使用额定工作点得到的损耗曲线，曲线2 是在不同转速下使用对应的最优磁链得到的损耗曲线，可以看出，在轻载模式下，节能效果非常明显。

4.4 试验结果

根据上面的分析，我们在一台350 kW 的鼠笼型风力发电变流器实验平台上进行了效率优化算法的试验验证。控制发电机工作在500 r/min，设定原动机输入转矩为506 N·m。

试验系统中为了避免不必要的电流冲击，各给定值采用阶梯波给定的方式代替阶跃给定，如图12a中磁链给定所示。4 s时刻，磁链给定值从1.89 Wb（额定磁链）逐渐改变到设计的最优点0.83 Wb。对应的系统发电功率如图12 b 所示，输出功率从19.5 kW 左右增大到22 kW，可见，试验结果与仿真结果基本一致。验证了方法的正确性。

图12 试验结果曲线Fig.12 Curves of experimental results

5 结论

本文考虑低风速工况下发电机效率的优化问题，建立了感应发电机的损耗模型；该模型将铁损电阻作为时变因子处理，从而使模型更精确，适应损耗模型法的特点；并提出在按转子磁链定向的矢量控制中，将损耗模型法求得的最优磁链作为输入，可以有效实现节能。通过仿真和试验，对比了额定磁链和最优磁链给定下对应的响应曲线，验证了本文方法获得的最优磁链实现节能的有效性。

［1］Thanga Raj C，Srivastava S P.pramod Agarwal.Energy Efficient Control of Three-phase Induction Motor-A Review［J］.International Journal of Computer and Electrical Engineering，2009，1（1）：793-8198.

［2］Durval de Almeida Souza，Wilson C P de Aragão Filho，Gilberto Costa Drumond Sousa.Adaptive Fuzzy Controller for Efficiency Optimization of Induction Motors［J］.IEEE Transactions on Industry Electronics，2007，54（4）：2157-2164.

［3］刘红星.异步电机自适应矢量控制系统的研究［D］.郑州：郑州大学，2007.

［4］张立伟，温旭辉，郑琼林.异步电机用混合式模糊搜索效率优化控制研究［J］.中国电机工程学报，2007，27（27）：83-87.

［5］张立伟.电动汽车用异步电机系统效率优化控制研究［D］.北京：中国科学院研究生院，2006.

［6］汤蕴璆，史乃.电机学［M］.北京：机械工业出版社，2005.

［7］李华德.电力拖动控制系统［M］.北京：电子工业出版社，2006.

［8］陈伯时.电力拖动自动控制系统［M］.第2 版.北京：机械工业出版社，1992.

［9］李宗臣.基于矢量控制的异步电机效率优化控制研究［D］.北京：北京交通大学，2010.

［10］Lin Youjie.Asynchronous Motor′s Maximum-efficiency Control Considering Variable Iron Loss Equivalent Resistance by Adjusting the Ratio of Active Power to Reactive Power［C］//International Conference on Electrical and Control Engineering，2010：3396-3399.

［11］Ernil Levi.Impact of Iron Loss on Behavior of Vector Controlled Induction Machines［J］.IEEE Transactions on Industry Applications，1995，31（6）：1287-1296.

［12］Levi E，Boglietti A，Pastrorelli M.Iron Loss in Rotor-flux Oriented Induction Machines：Identification，Assessment of Detuning，and Compensation［J］.IEEE Transactions on Power Electronics，1996，11（5）：698-709．

［13］刘小虎，谢顺依，郑力捷.一种改进的感应电机最大效率控制技术研究［J］.中国电机工程学报，2007，25（6）：95-98.

［14］Chandan Chakraborty，Yoichi Hori.Fast Efficiency Optimization Techniques for the Indirect Vector-controlled Induction Motor Drives［J］.IEEE Transactions on Industry Applications，2003，39（4）：1070-1076.

［15］李健健，刘新正.基于矢量控制的异步电动机节能运行的研究［J］.微电机，2010，43（3）：14-17.