人工冻土蠕变非定常开尔文模型
2014-06-26姚兆明
毛 芬,姚兆明
(安徽理工大学土木建筑学院,安徽 淮南 232001)
近年来,冻结法施工的应用越来越广泛,因此对人工冻土的蠕变本构关系的研究必不可少,人工冻土作为一种特殊的岩土类材料,由于土中冰包裹体和未冻的黏滞水膜的存在,使得建立冻土材料的本构模型比较困难,开尔文模型被发现是一个解决力学建模难题的有力工具,目前的研究多倾向于用定常模型来模拟岩石蠕变本构关系。常用的岩石蠕变模型有西原正夫模型、伯格斯模型和宾厄姆模型等,以上这些模型在岩土工程界具有重大影响,但它们都是基于传统的经典黏弹性定常本构模型建立起来的,鉴于非定常算子在黏弹性本构建模方面具有的一些优越性[1-2],本文拟采用引入与时间有关的非定常参数的开尔文模型来模拟人工冻土在一维单向压缩条件下的蠕变过程,在该模型中开尔文模型的黏滞系数η被与时间有关的函数代替。通过推算可以得到含非定常的人工冻土蠕变模型。
岩石力学理论与工程实践中的重要课题之一是本构模型的参数辨识。目前蠕变模型参数辨识方法主要有:回归方法、最小二乘法及其改进方法、模式搜索法以及蠕变曲线分解法等[3]。以上的优化算法都对问题有一定的约束条件,如要求优化函数可微等。粒子群优化算法作为一种仿生算法是一种模拟生物智能行为的优化算法,该算法利用生物群体内个体的合作和竞争等复杂行为产生群体智能,由于其几乎不存在对问题的约束,因此粒子群优化算法在各种优化问题中得到广泛应用[4]。粒子群优化算法是一种新兴的演化群体智能算法,其采用速度-位置搜索模型,每个例子代表解空间的一个候选解,解的优劣程度由适应度函数来决定[5-6]。运用模拟退火粒子群优化方法,对不同加载应力下蠕变试验数据建立的蠕变模型参数进行识别,得到蠕变模型的参数。
最后通过对比非定常蠕变模型计算值与试验结果,发现非定常开尔文蠕变模型能很好地模拟人工冻土的蠕变规律。非定常开尔文模型是人工冻土领域计算的一种新方法。
1 模型的建立
1.1 广义开尔文模型
广义开尔文模型由弹簧Ek和阻尼器并联,然后串联弹簧E1而成(见图1)。
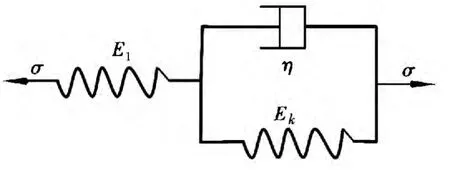
图1 广义Kelvin模型
根据模型特点,可以推出本构方程。
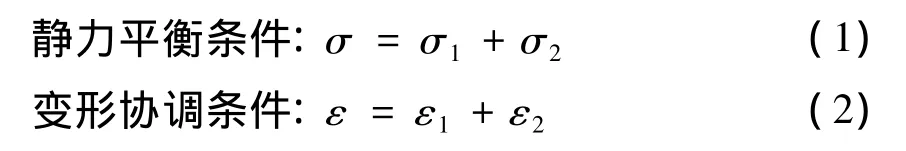
式中:σ,ε分别为模型的总应力和总应变;σ1,ε1分别为元件E1的应力和应变;σ2,ε2分别为元件并联体的应力和应变。
设应力为常量:σ=σ1=σ2=σ0=const元件E1的本构关系为

并联体的本构关系为
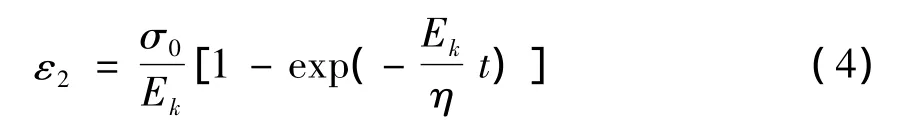
广义开尔文模型本构方程为
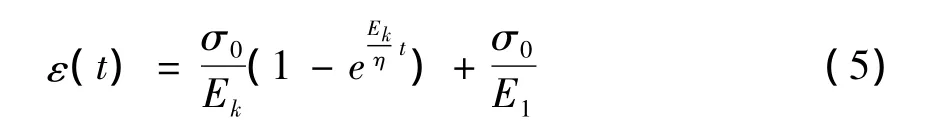
式中:Ek为开尔文体中弹簧的弹性模量;E1为串联弹簧的弹性模量;η为广义开尔文体中黏壶的黏滞系数;t为时间。
1.2 非定常开尔文模型
非定常开尔文模型就是用与时间有关的函数替代广义开尔文模型中的黏滞系数η和串联的的弹性模量E1。
根据文献[7],可设开尔文模型中黏壶η1随时间的变化满足:

式中:η0,α 为常数。
定常弹簧Ek与非定常黏壶η1(t)组成的非定常开尔文模型满足:
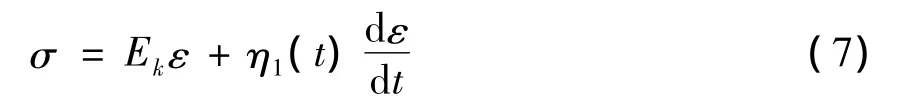
分离变量求定积分:
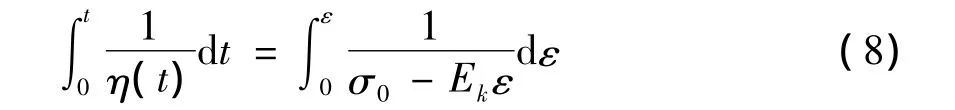
求出非定常开尔文的模型的蠕变柔量为

从而,得到非定常开尔文模型的本构方程为
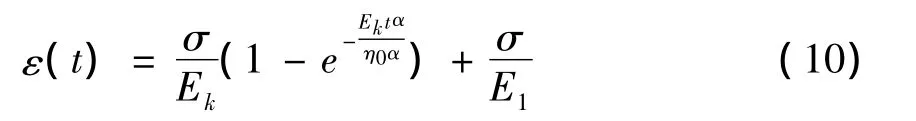
1.3 粒子群算法的描述
粒子群优化算法是基于群体智能理论的优化算法,通过群体中粒子间的合作与竞争产生的智能指导优化搜索[8],为工程优化问题提供高效的解决方法。
在粒子群优化算法中,每个优化问题的潜在解都是搜索空间中的一只鸟,称之为“粒子”。所有的粒子都有一个由被优化的函数决定的适应值,每个粒子还有一个速度决定他们飞翔的方向和距离。粒子们就追随当前的最优粒子在解空间中搜索。优化开始时先初始化为一群随机粒子(随机解)。然后通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个极值来更新自己。第一个极值就是整个种群目前找到的最优解。这个极值是全局极值。另外也可以不用整个种群而只是用其中一部分作为粒子的邻居,那么在所有邻居中的极值就是局部极值。邻近种群数是在最优粒子附近的种群个数。第二个极值是粒子本身所找到的最优解,称为个体极值。这是因为粒子仅仅通过跟踪全局极值或者局部极值来更新位置,不可能总是获得较好的解。这样在优化过程中,粒子在追随全局极值或局部极值的同时追随个体极值则圆满的解决了这个问题。这就是粒子群优化算法的原理[9-10]。
基本粒子群优化算法可描述如下:
设在一个D维的目标搜索空间中,有k个粒子组成一个群落,第i个粒子的位置用向量Xi=[Xi1,Xi2,…,XiD]表示,飞行速度用 Vi= [Vi1,Vi2,…,ViD]表示,第i个粒子搜索到最优位置为Pi=[Pi1,Pi2,…,PiD],整个群体搜索到的最优位置为Pg= [Pi1,Pi2,…,PiD],则用下列式更新粒子的速度和位置:

式中:i=1,2,…,m,表示不同的粒子;c1,c2为大于0的学习因子,是分别调节该粒子向自己寻找到的最优位子,和同伴已寻找到的最优位置方向飞行的最大步长;r1,r2为介于[0,1]之间的随机数;n为迭代次数,即粒子的飞行步数。
将V限定一个范围,使粒子每一维的运动速度都被限制在[-Vmin,Vmax]之间,以防止粒子运动速度过快而错过最优解,这里的Vmax根据实际问题来确定。当粒子的飞行速度足够小或达到预设的迭代步数时,算法停止迭代,输出结果[11]。
2 应用实例
2.1 人工冻土单轴蠕变试验
通过单轴压缩常规试验可以确定单轴加卸载蠕变试验的加载水平,试验选用安徽界沟矿区,土质为粘土,取土深度为61.2~70.1m。试验在WDT-100型微机控制电液伺服冻土单轴试验机中进行,试样尺寸为Φ50 mm×100 mm。在三个温度水平下、三种加载系数下的单轴蠕变试验,试样的单轴抗压强度如表1~表2所示。

表1 不同温度下的单轴抗压强度
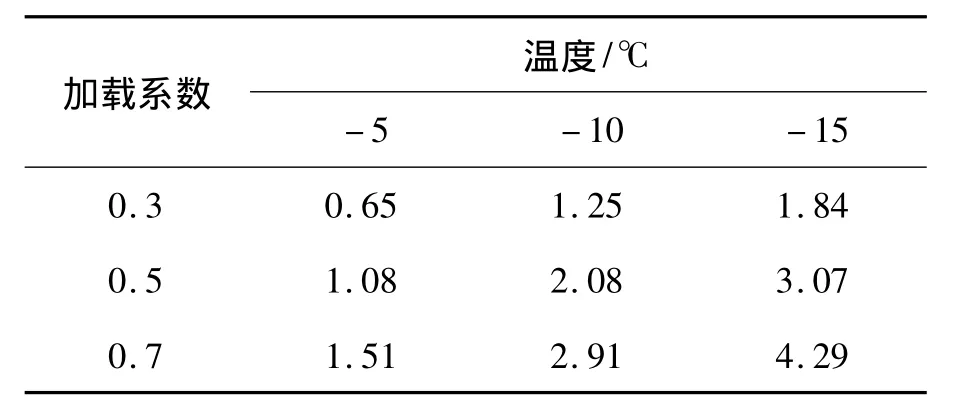
表2 不同温度和加载系数下的单轴抗压强度 (MPa)
2.2 试验验证
采用粒子群算法来优化分数阶导数蠕变模型参数,非定常开尔文蠕变模型参数如表4所示。
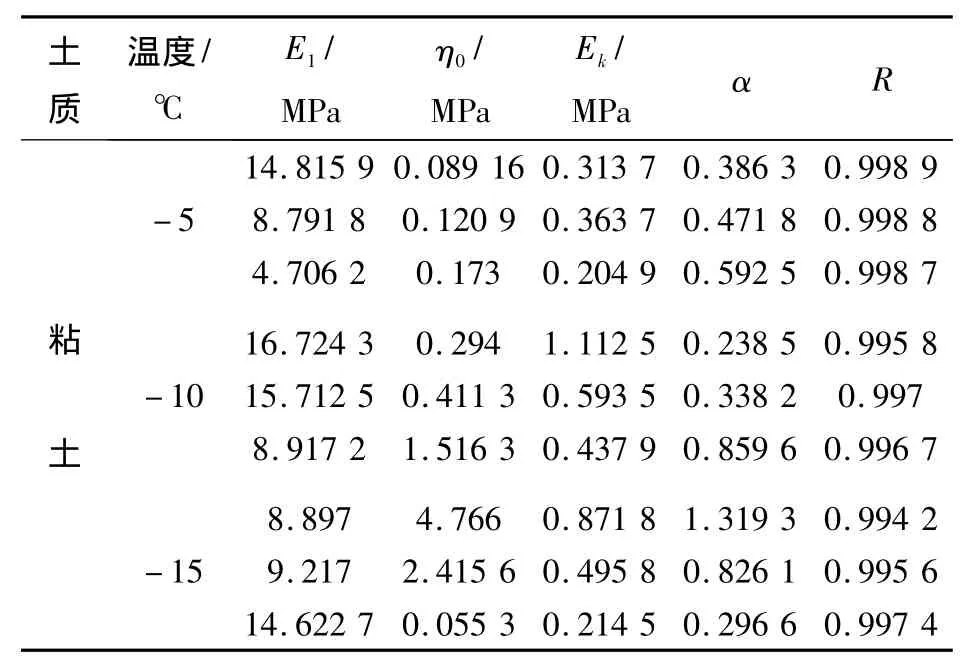
表3 非定常开尔文模型参数
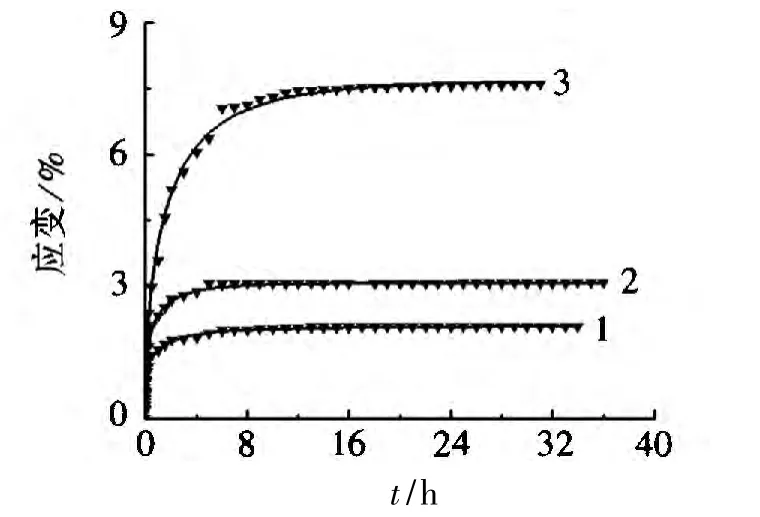
——试验值;▼非定常开尔文计算值1.σ=0.65MPa;2.σ=1.08MPa;3.σ=1.51MPa(a)-5℃下试验值和非定常开尔文计算值
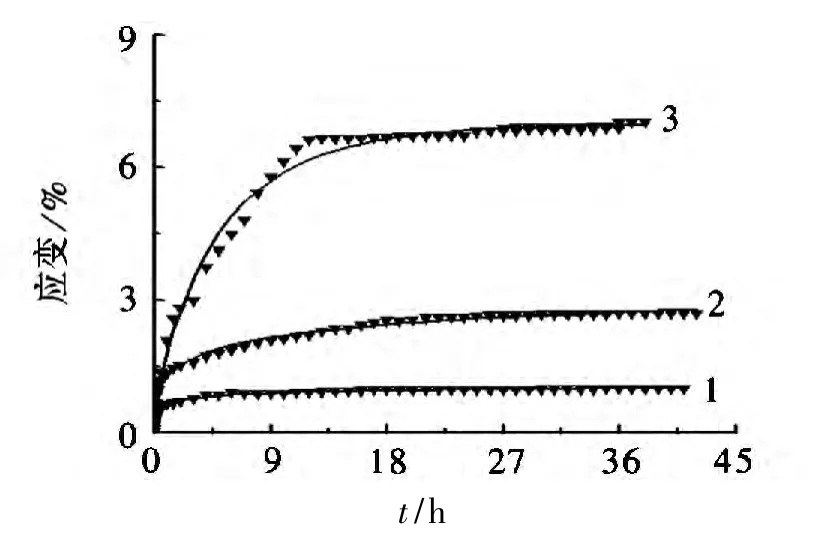
——试验值;▼非定常开尔文计算值1.σ=1.25MPa;2.σ=2.08MPa;3.σ=2.91MPa(b)-10℃下试验值和非定常开尔文计算值
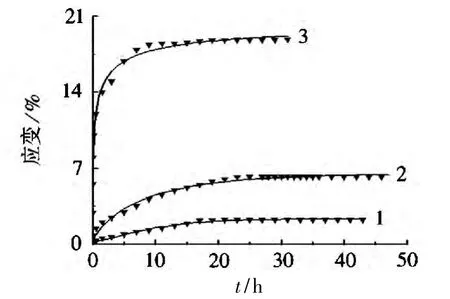
图2 单轴蠕变试验值与模型计算值对比
3 结论
用非定常开尔文模型来模拟人工冻土的蠕变过程,不仅具有明确物理意义参数,而且能与试验结果很好地拟合。
1)考虑到某些参数会受到时间的影响,以广义开尔文模型为基础,建立了非定常开尔文蠕变模型,其公式推导严密,模型具有明确的物理意义且模型参数少;
2)用非定常开尔文模型结合粒子群优化方法对不同温度下的蠕变规律进行了模拟,得到了相应的参数。
3)通过与试验值对比,发现非定常开尔文模型能很好的模拟蠕变曲线,相关系数基本都在0.995以上,为人工冻土领域的计算提供了一个新思路。本文只研究了一种土性的模拟,研究模拟结果比较好,是否能很好的模拟其他土性和是否能很好的模拟其他温度的蠕变模型将是下一步研究的方向。
[1]康永刚,张秀娥.岩石蠕变的非定常分数伯格斯模型[J].岩土力学,2011,32(11):3 237-3 241.
[2]康永刚,张秀娥.基于Burgers模型的岩石非定常蠕变模型[J].岩土力学,2011,32(S1):424 -427.
[3]朱珍德,徐卫亚.岩体黏弹性本构模型辨识及其工程应用[J].岩石力学与工程学报,2002,21(11):1 605-1 609.
[4]KENNEDY J,EBERHART R.Particle swarm optimization[C]//Proc.IEEE Int.Conf.on Neural Networks,1995:1 942-1 948.
[5]王章国,匡亚莉,林喆,等.基于粒子群算法的重介质分选产品结构优化[J].煤炭学报,2010,35(6):998-1 001.
[6]高鹰,谢胜利.基于模拟退火的粒子群优化算法[J].计算机工程与应用,2004(1):46-49.
[7]熊良宵,杨林德,张尧.岩石的非定常Burgers模型[J].中南大学学报:自然科学版,2010,41(2):679 -684.
[8]罗润林,阮怀宁,孙运强,等.一种非定常参数的岩石本构模型[J].桂林工学院学报,2007,27(2):200 -203.
[9]周驰,高海兵,高亮,等,粒子群优化算法[J].计算机应用研究,2003(12):7-11.
[10]KENNEDY J,EBERHART R.Particle Swarm optimization[C]//In:IEEE Int 1 Conf on Neural Networks.Perth,Austraial,1995:1 942 -1 948.
[11]罗润林,阮怀宁,朱昌星.基于粒子群-最小二乘法的岩石流变模型参数反演[J].辽宁工程技术大学学报:自然科学版,2009,28(5):750 -753.
