ρ混合序列部分和的强大数定律

沈建伟

1 预备知识

ρ～混合序列是一类极为广泛的相依混合序列。对于混合序列的研究已取得了不少成果。Bradley［1］研究了其极限定理；Peligrad等［2］讨论了混合序列的几乎处处收敛性；吴群英［3－5］得到了混合序列的若干收敛性质及其加权和的完全收敛性和强收敛性，并研究了ρ～混合序列的线性模型M估计的强相合性；韦静等［6］得到了混合序列加权和最大值的几乎处处收敛性；胡学平等［7］得到了混合序列部分和的若干收敛性质，推广了文献［3］中的结论；Guo等［8］研究了行混合阵列加权和的矩完全收敛性；沈建伟［9］给出了混合序列部分和的一个强大数律。

下面给出ρ～混合序列的定义及与本研究相关的一些引理。为行文方便，总是假设c代表正常数，在不

同的地方可以代表不同的值；用“≪”代表通常意义下的“O”。记代表集A的示性函数。

设｛Xn，n≥1｝是定义在概率空间（Ω，A，P）上的随机变量序列，FS＝σ（Xi，i∈S⊂ℕ）；Fn1＝σ（Xi，i≤n），F∞n＋k＝σ（Xi，i≥n＋k）为σ－域。在A中给定σ－域F和R。令

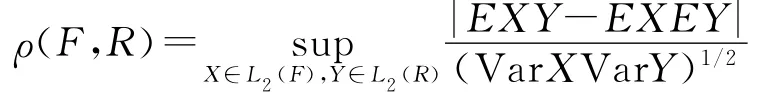
对k≥0，令

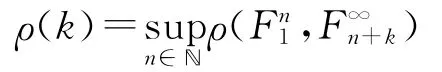
定义1 对随机序列｛Xn，n≥1｝，若存在k∈ℕ，使得（k）＜1，则称｛Xn，n≥1｝为ρ～混合序列。

引理1［10］设｛Xn，n≥1｝为ρ～混合序列，EXn＝0，E｜Xn｜p＜∞，对某些p≥2和任意n≥1，则存在与n无关的正常数D使得

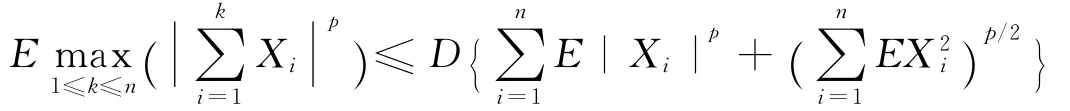
引理2［11］设｛an，n≥1｝是非降的正常数列，且对某个常数c有c＜∞。若对∀ε＞0，有，则

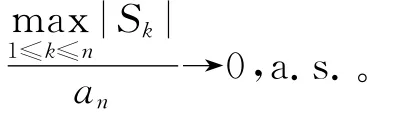
2 主要结果

定理1 设｛Xn，n≥1｝为ρ～混合序列，｛an，n≥1｝是常数列且满足0＜an↑∞，且对某个常数c有1≤。g（x）是定义在R R上的偶函数，且在区间x＞0中取正值、不减；函数g（x）满足下列条件之一：

假定

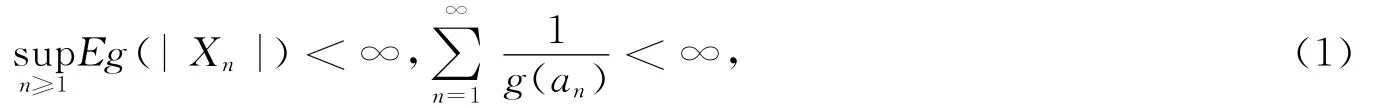
在定理1中，令g（x）＝｜x｜p，p＞0，可得

推论1 设｛Xn，n≥1｝为混合序列，｛an，n≥1｝是常数列，满足0＜an↑∞，且对某个常数c有＜p≤2，且1＜p≤2时EXn＝0。假定则→0，a.s.。

在推论1中，取an＝［n（log n）1＋δ］1／p，δ＞0，有

推论2 设｛Xn，n≥1｝为ρ～混合序列，0＜p≤2，且1＜p≤2时EXn＝0。假定E｜Xn｜p＜∞，则对于

注：此结果直接推广了文献［3］中推论3的结果。

在定理1中，令g（x）＝x2，取an＝nα（log n）β，α＞0，β≥0，有

推论3 设｛Xn，n≥1｝是均值为零的ρ～混合序列，假定

定理1的证明 记Xann ＝XnI（｜Xn｜≤an）

假设g（x）满足条件1），可得

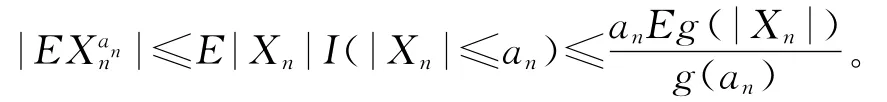
假设g（x）满足条件2），注意到EXn＝0可得

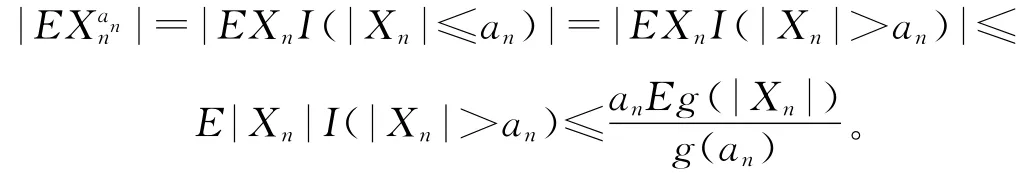
故无论g（x）满足条件1）或2），都有

从而由式（1）、式（2）可得

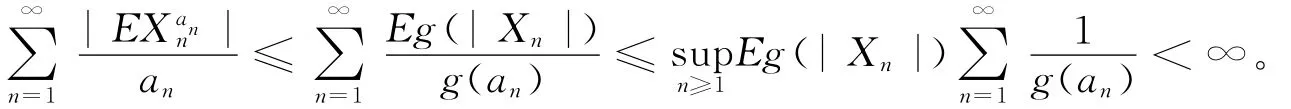
由Kronecker引理得

由Chebyshev不等式及式（1）可知

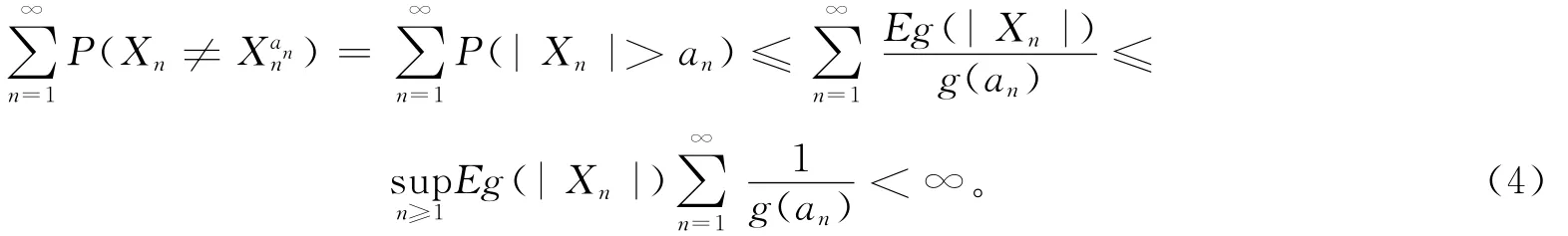
由式（3）、式（4）及Borel－Cantelli引理可知，要证明定理成立，只需证明

假设g（x）满足条件1），则在区间｜x｜≤an中，可得

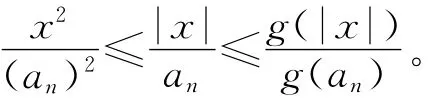
假设g（x）满足条件2），则在区间｜x｜≤an中，可得

因此，无论g（x）满足条件1）或条件2），在区间｜x｜≤an中，都有

结合式（6），｛an，n≥1｝为一非降、趋于无穷的正常数列可知

由 Mar kov不等式、引理1、式（6）、式（7）和式（1）可得

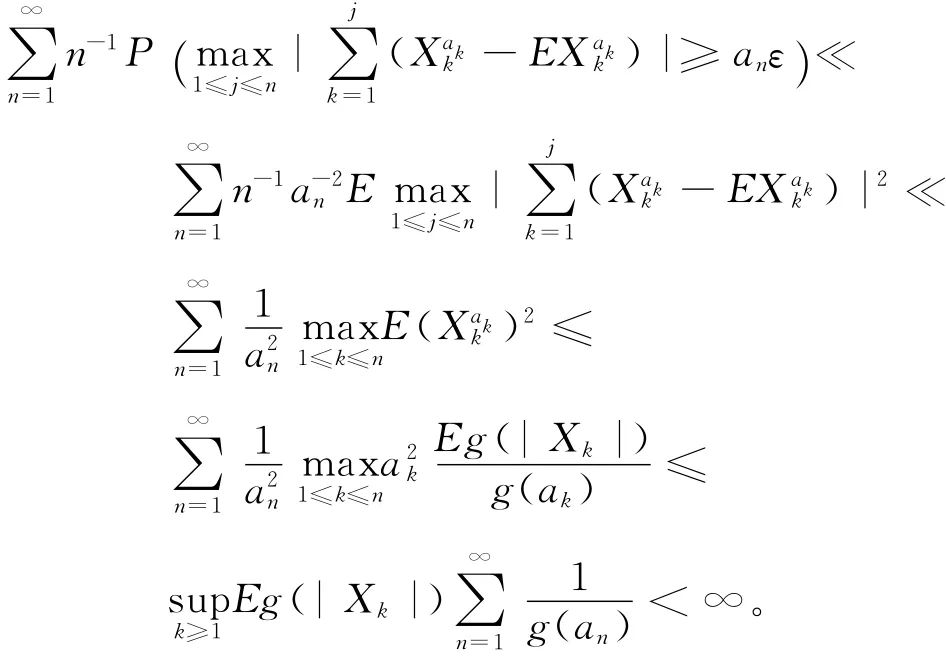
由引理2可得定理1结论成立。

从定理的证明过程可知，该结果主要是利用了文献［11］中关于证明强大数律的一般方法并结合ρ～混合序列的矩不等式得到的。利用该方法，也可得到其他一些相依序列关于强大数律的结论。

［1］ Bradley R C.On the spectral density and asy mptotic nor mality of weakly dependent random fields［J］.Journal of Theoretical Probability，1992，5（2）：355－373.

［2］ Peligrad M，Gut A.Al most－sure results for a class of dependent random variables［J］.Journal of Theoretical Probability，1999，12（1）：87－104.

［3］ 吴群英.ρ混合序列的若干收敛性质［J］.工程数学学报，2001，18（3）：58－64，50.

［4］ 吴群英.ρ混合序列加权和的完全收敛性和强收敛性［J］.应用数学，2002，15（1）：1－4.

［5］ 吴群英.ρ～混合线性模型 M 估计的强相合性［J］.数学物理学报，2005，25（1）：41－46.

［6］ 韦静，唐国强.ρ～混合随机变量序列加权和最大值的几乎处处收敛性［J］.桂林理工大学学报，2011，31（4）：633－636.

［7］ 胡学平，桂春燕.ρ～混合序列部分和的若干收敛性质［J］.数学杂志，2012，32（3）：521－528.

［8］ Guo M L，Dong J，Ren Y.Complete mo ment conver gence of weighted su ms for arrays of rowwiseρ＊－mixing rando m variables［J］.应用数学，2013，26（1）：18－27.

［9］ 沈建伟.ρ～混合序列的一个强大数律［J］.浙江科技学院学报，2013，25（5）：325－328.

［10］ Utev S，Peligrad M.Maxi mal inequalities and an invariance principle f or a class of weakly dependent random variables［J］.Jour nal of Theoretical Probability，2003，16（1）：101－115.

［11］ Yang S C，Su C，Yu K M.A general method to the strong law of large numbers and its applications［J］.Statistics ＆Probability Letters，2008，78（6）：794－803.