基于改进动态自适应粒子群优化算法的汽轮机组给水回热分配优化方法
2014-06-25付文锋王蓝婧杨勇平
付文锋,王蓝婧,李 飞,杨勇平
(1.华北电力大学 电站设备状态监测与控制教育部重点实验室,保定071003;2.华北电力大学 计算机系,保定071003)
汽轮机组的给水回热系统既是汽轮机热力系统的基础,也是电厂热力系统的核心,它对机组和电厂的热经济性起着决定性的作用,合理选择给水回热循环的热力参数,使之达到最佳配合是有效降低发电厂能耗的关键[1-2].其中,给水在各加热器中的焓升分配是影响回热循环热经济性的重要参数之一,实现对加热器给水焓升分配的优化,可以在不增加设备投资和材料消耗的情况下获得一定的经济效益.因此,针对给水回热分配问题,曾有学者进行了大量的研究工作,提出了多种寻找最佳回热分配的方法.经典的分配方法有焓降分配法、平均分配法和几何级数法等[3],这些方法通过简化循环、推导通式,为之后的研究工作提供了理论指导.一些学者在此基础上,考虑实际系统中的各种具体因素,应用循环函数或等效焓降等方法[4-5],结合规划原理或遗传算法等寻优方法对现有热力系统进行优化,取得了一定的成果[6-7].但是,现有的这些方法相对繁琐、复杂且通用性和精度不高,目前还没有出现一种精确、简单、通用且行之有效的方法来解决这一问题.
粒子群优化(PSO)[8-9]算法作为一种基于群智能的启发式进化算法,具有搜索效率高、计算简洁和易于实现等优点,已被广泛应用于函数优化、神经网络训练、系统控制、工作调度和工业设计等诸多领域,并表现出良好的性能.但是,PSO 算法也表现出一些缺点,如求解高维复杂问题时容易早熟收敛;在进化后期,由于缺乏有效的机制使算法逃离局部极值,使得算法的收敛速度变慢,当接近最优解时,算法停滞,导致精确度受到限制.为解决这些问题,许多学者进行了各种尝试,其中一种方式是通过调整惯性权重来改进算法性能,如线性递减权重[10]、模糊自适应权重[11]、非线性权重[12]、随机权重[13]和动态自适应权重[14]等.
笔者将PSO 算法应用于汽轮机组给水回热分配优化问题,首先对基于进化状态的自适应粒子群算法进行了改进,提出了新的惯性权重更新策略,并构造了基于PSO 算法的汽轮机组给水回热分配的计算框架,最后将改进算法应用于某1 000 MW 汽轮机组给水回热分配问题.
1 标准PSO 算法
PSO 算法起源于对鸟类觅食行为的模拟,由Eberhart和Kennedy于1995年提出.算法初始化时,对每个粒子的状态随机赋值,然后根据式(1)和式(2)来更新它们的速度和位置.

式中:c1和c2为加速系数,一般取c1=c2=2;r1和r2为2 个独立的均匀分布在[0,1]内的随机数;vi∈[-Vmax,Vmax],Vmax是为了遏止过度漫游粒子而定义的一个常数;ptid为第i个粒子在t次迭代中搜索到的最好位置在第d维的分量;gtid为整个群体在t次迭代中搜索到的最好位置在第d维的分量.
为了提高算法的收敛性能,Shi通过修改式(1)对原始的PSO 算法进行了如下改进

式中:ω为惯性权重因子.
上述POS 算法在大多数文献中被称为标准PSO 算法.
2 PSO 算法的改进
2.1 改进的PSO 算法
在动态自适应算法[14]中,基于收敛准则并不要求粒子速度最终趋于零,给出了如下粒子的速度和位置更新公式

与传统PSO 算法相比,速度更新式(4)有2个不同的特点:(1)r1和r2的值仅随粒子数量和迭代次数随机改变,即在第t+1 次迭代中,第i个粒子在每个维度中都有相同的随机值;(2)惯性权重也随着粒子数和迭代次数而不同.
进化速度因子和聚集度因子是动态自适应PSO 算法在搜索过程中的两类特征参数,惯性权重值随进化速度因子和聚集度因子的变化而不断变化,变化的目的是使算法具有更出色的搜索能力和跳出局部最优的能力.与文献[14]中不同,笔者采用如下方法定义进化速度因子和聚集度因子.
进化速度因子:

式中:F(pt-1i)为pt-1i的适应值;h在[0,1]之间,h值越大,粒子的进化速度越快.
聚集度因子:

式中:Ft为第t次迭代中的最佳适应值;为第t次迭代中的平均适应值;N为种群规模;L为搜索空间的最长半径;D为解空间的维数;pid为第i个粒子的第d维坐标;为所有粒子第d维坐标的平均值.
按照上述定义可知,s1和s2均在[0,1]之间,s1表征了粒子进化中体现在适应值上的分布状态,s2表征了粒子进化中体现在空间距离上的分布状态.与文献[14]相比,笔者通过2种聚集度因子可以从不同角度更全面地描述粒子的进化状态.
参考自然界中鸟类的觅食习惯:个体(如一个粒子)在搜索过程中,如果找到对象的可能性增加(即h相对较大),它将不急于加速到下一个位置,而是减速(即减小惯性权重)飞向最优位置,这导致目前搜索区域的搜索强度增加,以便更快地找到最优位置.否则,需要扩大搜索范围继续寻找.同时,为了加强算法跳出局部最优的能力,当某一代的适应值趋于稳定(即s1趋于较大值时),应增大粒子群的搜索空间(即增大惯性权重).特别地,在进化后期(h相对较小),如果粒子没有能够迅速找到最优位置,出现粒子之间相对集中而适应度值并不稳定的情况时(即s2较大而s1较小),应收缩空间进行更细致的搜索(即减小惯性权重).
综上所述,在本文中惯性权重按下式给出

式中:α、β在[0,1]内选择,取α=β=0.5;a、b为控制聚集度因子的阈值,一般取a=0.9,b=0.5.
2.2 算法测试与对比试验
为了评价所提出的改进算法的求解性能,采用4个基准测试函数(见表1)进行分析.其中,x*为全局最优点,f(x*)为全局最小值.这些测试函数具有不同的特点,可以充分考察算法对不同类型问题的优化性能,并有效检验算法的全局搜索性能和避免早熟收敛的能力.

表1 4个标准测试函数Tab.1 Four benchmark functions used for assessment purpose
选取近年来提出的多个PSO 算法的变种与本文算法进行比较.为了清晰地对比各种算法对测试函数的性能,对表1中的基准函数设置了相同的参数(见表2)进行测试.

表2 测试函数的参数设置Tab.2 Parameter setting for the test functions
用于对比的多个PSO 算法变种描述如下:
(1)惯性权值线性递减PSO 算法(PSO_w)[10];
(2)收 缩 因 子 局 部PSO 算 法(PSO_cf_local)[15];
(3)基于适应度距离比例POS 算法(FDR_PSO)[16];
(4)互联型PSO 算法(FIPS)[17];
(5)综合学习PSO 算法(CLPSO)[18];
(6)动态自适应PSO 算法(DAPSO)[14];
(7)本文算法(DAPSO_ex).
对f1~f4,每种算法被连续运行20次.表3给出了在最大迭代次数内,各种算法分别在20次优化计算时所得到的最优适应度值和最差适应度值,适应度值以函数值表示.其中,PSO_cf_local和FIPS的数据来自文献[18],PSO_w、FDR_PSO 以及CLPSO的数据来自文献[19],DAPSO 和DAPSO_ex的数据来自本文试验.
由表3可知,在最大迭代次数内,DAPSO_ex对上述4个函数的优化均取得了最好的求解精度.对于f1和f3,本文算法在20次试验中均能收敛于全局最优解;对于f2,新算法能收敛于精度较高的局部最优点8.881 8×10-16,仅有1次陷入较差的19.950 4;对于f4,本文算法能收敛于精度较高的局部最优点1.272 8×10-4.试验结果表明,新算法的求解精度和稳定性明显高于其他PSO 变种算法.
3 基于PSO 算法的汽轮机组给水回热分配模型
3.1 循环热效率的计算
对于一般的大型汽轮机组一次再热给水回热系统(见图1),由于系统热经济性的优劣可用循环热效率η来评价,所以建立数学优化模型的基础工作是进行机组循环热效率的计算.
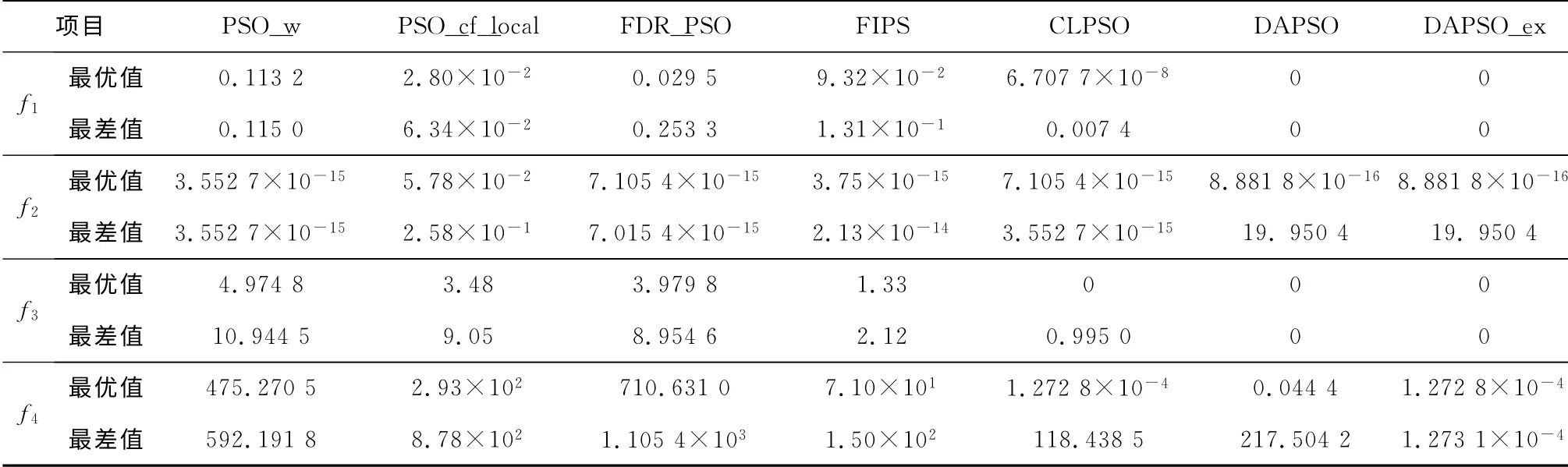
表3 测试函数试验结果Tab.3 Experimental results of the test functions
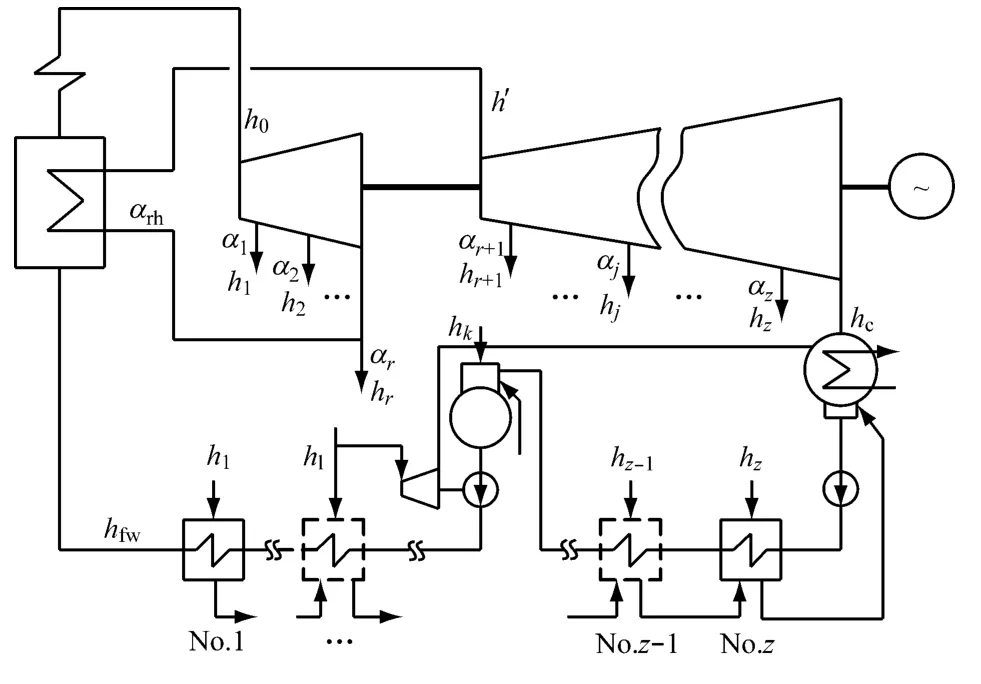
图1 现代大型汽轮机组一次再热给水回热系统示意图Fig.1 Typical single-reheat feedwater heating system of a large steam turbine unit
η可按式(10)计算:

式中:w为单位工质的循环做功量;q为单位工质的循环吸热量;h0为初蒸汽焓;hc为汽轮机排汽焓;hfw为锅炉给水焓;qrh为工质在再热器内的焓升;αj为汽轮机各抽汽流量份额;hj为汽轮机各抽汽焓;αrh为汽轮机再热蒸汽份额,αrh=1-α1-α2-…-αr;r为再热前的抽汽流个数;z为汽轮机抽汽个数.
由式(10)可知,计算η时需要首先确定汽轮机各抽汽焓hj和汽轮机各抽汽流量份额αj.
3.2 hj 的计算
根据汽轮机汽态膨胀线,可得hj的递推公式:

当j=r+1 时,有p′=(1-δp)pr,h′=fp,t→h(p′,t′).
式中:ηj为各级组的等熵效率;pj为各级抽汽压力;δp为再热压损系数;t′为再热温度;p′和h′为中压缸进汽压力和焓;fs,p→h、fh,p→s、fp,t→h分别为已知熵和压力求焓、已知焓和压力求熵、已知压力和温度求焓的函数关系式,可以由国际水和水蒸气性质协会提供的1997年工业用计算模型(IAPWS-IF97)确定.
所以hj可以表示为pj的函数,记为hj=fjp→h(p1,p2,…,pj).
3.3 αj 的计算
对于不同的回热加热器形式(见图2),有如下定义[4]:

图2 不同回热加热器形式Fig.2 Definition for different types of regenerative heaters
疏水放流式加热器:

汇集式加热器:

式中:hw,j为加热器出口水焓;hs,j为加热器疏水焓.
根据加热器疏水利用的不同方式,利用加热器的上端差和下端差,可将τj、qj、γj计算公式中加热器出口水焓hw,j和疏水焓hs,j转化为加热器内饱和水焓hb,j的函数.
当加热器不设置疏水冷却器时

当加热器设置疏水冷却器时

式中:θj和φj分别为用焓表示的加热器上端差和下端差.
考虑抽汽管路压损系数δpj后,可以求得加热器内的饱和水压力pb,j=(1-δpj)pj,即可以确定出加热器内饱和水焓hb,j=fpb→hb(pb),其中fpb→hb为IAPWS-IF97中已知压力求饱和水焓的函数关系式.
根据各加热器热量平衡和质量平衡推出下式

式中:A为z阶下三角矩阵;qf为主系统外的能量流,包括附加汽水能量流和给水泵焓升等,其书写规则详见文献[20].
A中元素ai,j(i为行、j为列)满足以下规则:当i<j时,ai,j=0;当i=j时,ai,j=qi;当i>j时,如果i号加热器接受j号加热器疏水,则ai,j=γi,否则ai,j=τi.
对于图1所示的一般性回热系统,式(16)可以展开成如下形式:

式中:k表示第k号加热器为除氧器;l表示小汽轮机与第l号加热器共汽源;(τfw)(k-1)表示τfw项位于qf中的第k-1项;τfw为给水泵焓升;αq为小汽轮机流量份额.
由式(17)得到的αj可以表示为pj的函数,记为αj=fjp→α(p1,p2,…,pj+1).
3.4 汽轮机组给水回热分配问题的优化数学模型
由式(10)、式(11)和式(16)可知,在其他设计条件(主蒸汽参数、终端参数、再热蒸汽温度、管道压损、加热器端差、排汽干度和加热器个数等)一定的条件下,以抽汽压力为优化变量,机组循环热效率为寻优目标,可以建立如下数学模型

约束 条件为:pc<pj<p0
式中:p0和pc分别为汽轮机组初压和排汽压力的设计值.
4 应用实例
某1 000MW 汽轮机组给水回热系统连接形式见图3.

图3 某1 000 MW 汽轮机组给水回热系统图Fig.3 Feedwater heating system of a 1 000 MW steam turbine unit
初始条件:主蒸汽压力p0=25 MPa,温度t0=600 ℃,再热蒸汽温度tr=600 ℃,汽轮机排汽压力pc=0.004 9 MPa,排汽干度为0.905,汽轮机抽汽个数z=8,各抽汽管路压损系数δpj=3%,小汽轮机和除氧器共用第4号抽汽(即l=k=4).各加热器的上、下端差见表4,各附加汽水能量流参数见表5.
选取种群规模为20,迭代次数为500,分别采用遗传算法(GA)[7]、基本粒子群算法(PSO)和本文改进粒子群算法(DAPSO_ex)各经过50次重复优化计算,得到3种算法的最佳适应度值进化曲线(见图4).

表4 各加热器的端差Tab.4 Terminal temperature difference of various feedwater heaters

表5 附加汽水来源及份额Tab.5 Sources and shares of additional steam
由图4可知,无论从求解精度方面或收敛速度方面,DAPSO_ex都优于GA算法和PSO算法.DAPSO_ex所得的优化结果与机组原设计值的比较见表6.
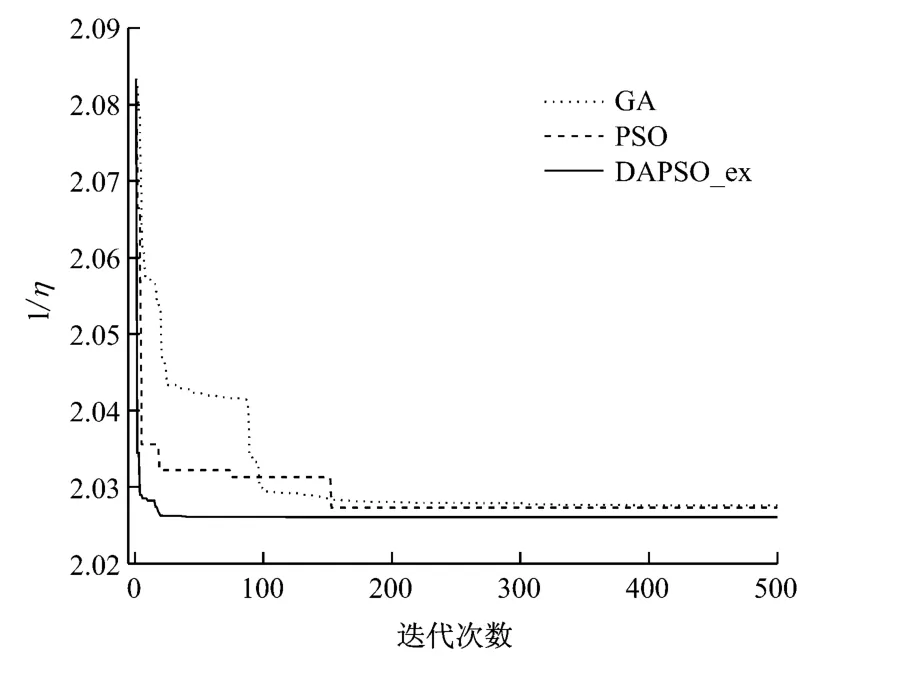
图4 最佳适应度值进化曲线Fig.4 Best fitness trend line for the optimization

表6 优化结果与原设计值的比较Tab.6 Comparisons between optimization results and original design values
如表6所示,在本优化实例中只针对1号、2号外的加热器所对应的抽汽压力进行优化,原因是1号、2号加热器抽汽压力分别影响给水温度和再热蒸汽压力,如果1 号、2 号加热器抽汽压力发生改变,汽轮机回热系统外的其他设备(如省煤器和再热器等)的选材和布置都需要进行重新设计和考虑.
由表6可以看出,优化后的机组循环热效率比原设计值相对提高了0.23%,若机组发电标准煤耗率以280g/(kW·h)计,年利用小时数以5 500h计,一台机组每年可以节约标准煤约3 526.38t,经济效益可观.
所提出的基于改进PSO 算法的给水回热分配优化方法比传统方法简捷、易实现、收敛精度更高,对回热系统或设备不需要进行任何假设(如假设没有再热和所有加热器都是混合型加热器等),便于考虑实际系统中各种具体因素,可以实现更加合理的最佳设计方案.
5 结 论
对基于进化状态的自适应粒子群算法中的聚集度描述进行了改进,试验证明改进的PSO 算法具有良好的性能.构造了通用性给水回热分配优化的数学模型,并将改进PSO 算法应用于汽轮机组给水回热分配问题.实例计算结果表明,该方法能迅速、准确地求得最优解.该方法可以推广应用于其他形式的机组,对大型汽轮机组热力系统挖掘节能潜力和优化设计具有一定的指导意义.
[1]LI Y,WANG C.Study on the effect of regenerative system on power type relative internal efficiency of nuclear steam turbine[J].Energy Procedia,2012,17:906-912.
[2]ALJUNDI I H.Energy and exergy analysis of a steam power plant in Jordan[J].Applied Thermal Engineering,2009,29(2/3):324-328.
[3]林万超.火电厂热系统节能理论[M].西安:西安交通大学出版社,1994:191-203.
[4]ZHANG C F,ZHAO N,LI L P.The variable load operation characteristic and energy-saving optimizing control system of power plant[C]//Proceedings of the Sixth International Conference on Machine Learning and Cybernetics.Hong Kong,China:IEEE,2007:443-448.
[5]CHEN H P,ZHANG C F,LIU J Z,etal.The calculating method of thermal system for the coal-fired power unit base on mass unit[C]//Proceedings of the International Conference on Power Engineering.Kobe,Japan:Japan Soc.Mechanical Eng,2003:3-157.
[6]邓世敏,迟全虎,金红光.汽轮机通流部分改造后机组的回热 系 统 优 化[J].动 力 工 程,2004,24(2):195-198. DENG Shimin,CHI Quanhu,JIN Hongguang.Optimization of the heat regenerative system after the modification of the flow path of the steam turbine[J].Power Engineering,2004,24(2):195-198.
[7]张俊礼,葛斌.遗传算法在压水堆核电机组给水回热分配中的应用[J].中国电机工程学报,2005,25(6):152-156. ZHANG Junli,GE Bin.Application of genetic algorithm in feed heating's distribution of PWR nuclear power unti[J].Proceedings of the CSEE,2005,25(6):152-156.
[8]KENNEDY J,EBERHART R C.Particle swarm optimization[C]//IEEE International Conference on Neural Networks Proceedings.Perth,Australia:IEEE,1995:1942-1948.
[9]EBERHART R C,KENNEDY J.A new optimizer using particle swarm theory[C]//Proceedings of the Sixth International Symposium on Micro Machine and Human Science.Nagoya,Japan:IEEE,1995:39-43.
[10]SHI Y H,EBERHART R C.A modified particle swarm optimizer[C]//IEEE International Conference on Evolutionary Computation Proceedings.Anchorage,AK,USA:IEEE,1998:69-73.
[11]NOROUZZADEH M S,AHMADZADEH M R,PALHANG M.LADPSO:using fuzzy logic to conduct PSO algorithm[J].Applied Intelligence,2012,37(2):290-304.
[12]LI L,XUE B,NIU B.The novel non-linear strategy of inertia weight in particle swarm optimization[C]//Proceedings of the Fourth International Conference on Bio-Inspired Computing.Beijing,China:IEEE,2009:183-187.
[13]EBERHART R C,SHI Y H.Tracking and optimizing dynamic systems with particle swarms[C]//Proceedings of the IEEE Congress on Evolutionary Computation.San Francisco,USA:IEEE,2001:94-100.
[14]YANG X M,YUAN J S,YUAN J Y,etal.A modified particle swarm optimizer with dynamic adaptation[J].Applied Mathematics and Computation,2007,189(2):1205-1213.
[15]KENNEDY J,MENDES R.Population structure and particle swarm performance[C]//Proceedings of the Congress on Evolutionary Computation.Honolulu,USA:IEEE,2002:1671-1676.
[16]PERAM T,VEERAMACHANENI K,MOHAN C K.Fitness-distance-ratio based particle swarm optimization[C]//Proceedings of the IEEE Swarm Intelligence Symposium.Indianapolis,USA:IEEE,2003:174-181.
[17]MENDES R,KENNEDY J,NEVES J.The fully informed particle swarm:simpler,maybe better[J].IEEE Transactions on Evolutionary Computation,2004,8(3):204-210.
[18]LIANG J J,QIN A K.Comprehensive learning particle swarm optimizer for global optimization of multimodal functions[J].IEEE Transactions on Evolutionary Computation,2006,10(3):281-295.
[19]吕艳萍,李绍滋,陈水利,等.自适应扩散混合变异机制微粒群算法[J].软件学报,2006,23(8):164-167. LÜ Yanping,LI Shaozi,CHEN Shuili,etal.Particle swarm optimization based on adaptive diffusion and hybrid mutation[J].Journal of Software,2006,23(8):164-167.
[20]张春发,张素香,崔映红,等.现行电力系统热经济性状态方程[J].工程热物理学报,2001,22(6):665-667. ZHANG Chunfa,ZHANG Suxiang,CUI Yinghong,etal.Thermo-economy state equation of modern power system[J].Journal of Engineering Thermophysics,2001,22(6):665-667.
