土壤地球化学测量在黄吉沟地区的找矿应用
2014-06-24罗俊峰
王 玉,罗俊峰,谢 刚
(四川省地质矿产勘查开发局一〇九地质队,成都 龙泉驿区 610100)
土壤地球化学测量在黄吉沟地区的找矿应用
王 玉,罗俊峰,谢 刚
(四川省地质矿产勘查开发局一〇九地质队,成都 龙泉驿区 610100)
通过对黄吉沟地区进行土壤地球化学测量,分别运用传统统计法和分形—求和法对Au、Cu、Bi、W的异常下限进行计算,并圈定了单元素异常图;确定了测区内的构造破碎带为Au、Cu有利富集区,而Bi、W与花岗岩密切相关。同时,在小范围尺度下,统计法在寻求主攻矿体时的作用明显,而分形法在矿体外围寻求找矿突破时实用性较强。
土壤地球化学测量;异常下限;找矿;黄吉沟
土壤地球化学测量在覆盖区的矿产勘查工作中应用日趋广泛,技术也日趋成熟;而元素地球化学异常下限值的确定是地球化学研究中的热点及难点之一[1]。确定异常下限方法繁多[2~7],只有多方法综合评价,因地制宜的应用,才能真实客观的体现元素的分布特征,为找矿靶区的遴选提供科学的地质依据。
以1∶1万土壤地球化学测量对测区的小比例尺水系综合异常进行分解,通过传统统计法和分形—求和法确定Au、Cu、Bi、W的异常下限圈定土壤地球化学单元素异常,并进行验证,取得了良好的找矿效果。
1 地质背景
黄吉沟地区出露的地层主要为早古生代中晚期的滩间山群中基性火山碎屑岩,经区域变质作用达绿片岩相;出露面积约占测区面积的85%。区内侵入岩以花岗岩为主,约占测区面积的13%。
测区总构造线呈北东、北西两组共轭方向。主要为中深构相韧性剪切带及伴生的浅构相韧性剪切带。它不仅控制着岩浆的活动、侵位分布,而其派生的次级断裂,也可为深部含矿热液活动、成矿元素的迁移和富集提供了有利通道和储矿空间。
2 异常下限值的确定
2.1 传统统计法
统计法的前提是元素分布符合正态分布或对数正态分布,然而实际情况往往不具这种理想的前提[8~9]。一般的处理方法是,通过对野值点进行剔除,再将剔除后的值进行对数化,使其基本符合对数正态分布。具体处理方法如下:
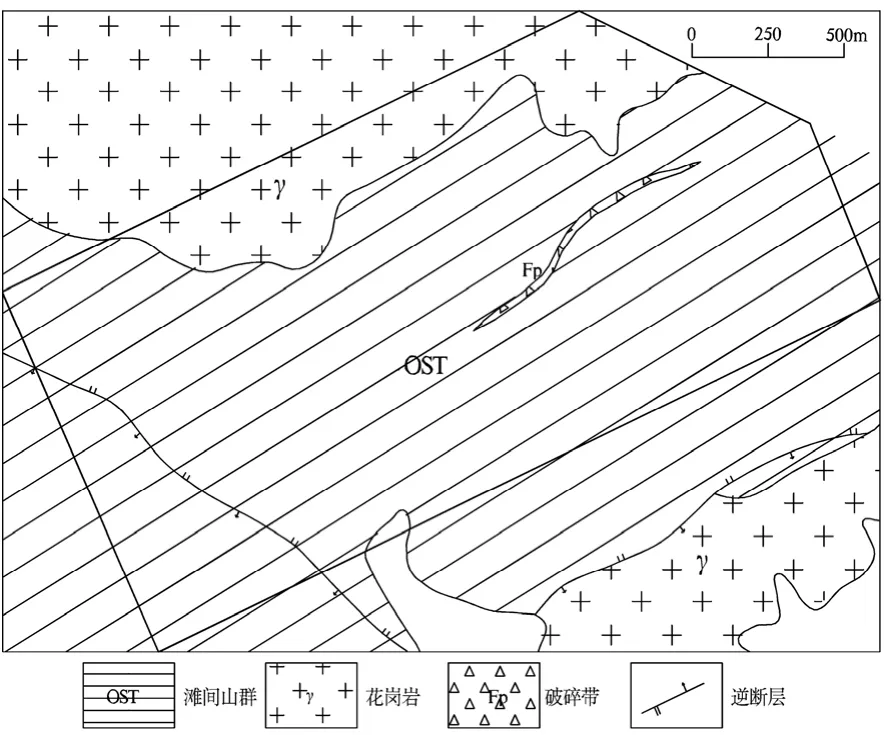
图1 测区地质简图

图2 频数分布直方图
1)首先对高值、低值进行剔除,一般采用平均值±3倍均方差为上下限进行迭代剔除,至无离群点数值为止。
2)将提出后的化探数据进行对数化,并进行分组,统计频数,制作频数分布直方图,用此来判断经处理后的数据是否具对数正态分布。也可通过偏度(R1)和峰度(R2)这两个指标来检验[10];在样品数(n)大于100,且置信度大于95%的情况下,同时满足R12<24/n,R22<2*24/n时,则服从正态分布,反之则不服从。
可以从图2和表1看出,Au、Cu、Bi、W仍不完全符合正态分布。这可能是由于测区本身处于小比例尺水系综合异常区内,频率分布可能有一个单一的背景全域和一个异常全域交迭而出现频率分布曲线呈不对称的偏斜。
此时可参照《地球化学普查规范》(DZ/T 0011—91)所介绍的方法,利用众值代替平均值,用众值左方的频率分布曲线推算右方曲线的方法来求得背景值。具体计算公式如下:
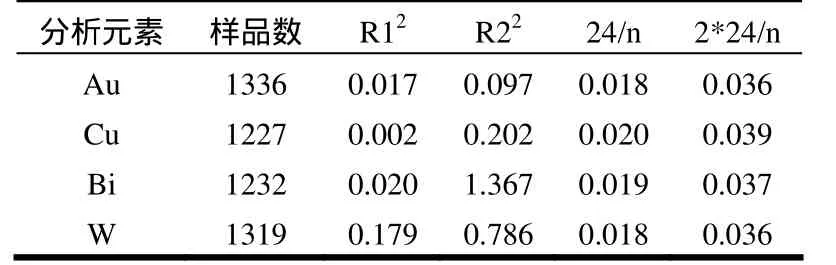
表1 正态检验表
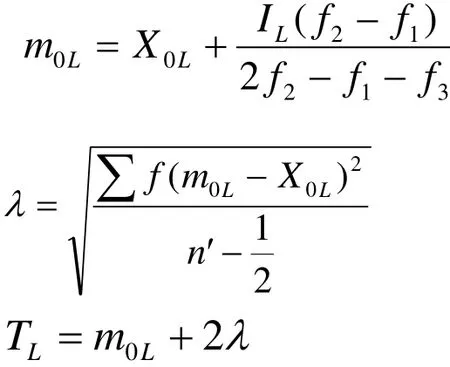
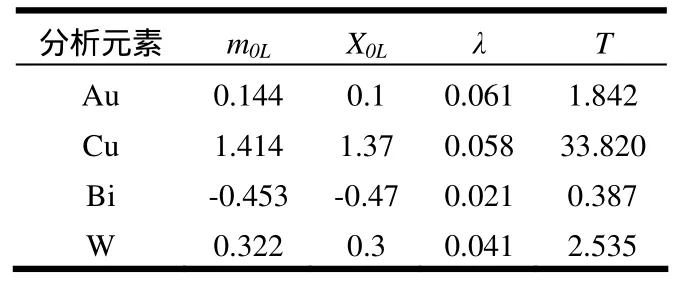
表2 传统统计法计算结果表
IL为对数组距;m0L为对数众值,X0L为众值所在组起点对数值; f1为众值所在组前一组频数;f2为众值所在组之频数;f3为众值所在组后一组之频数;′n为对数众值左方样品总数。TL为对数异常下限,异常下限T=10TL。测区计算结果表如表2。
2.2 分形—求和法
通过频数分布直方图和正态检验可以看出,各元素数据经处理后仍然并不服从正态分布,均呈一定程度偏斜,因此,本文再以分形法的分形—求和法计算各元素的异常下限值[8~9、11~12]。
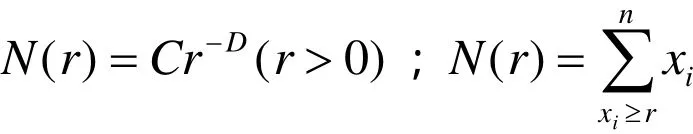

表3 分析—求和法计算结果表
上式为分形—求和模型;式中,r为含量的特征尺度,C>0为比例常数,D>0为一般分维数,xi(i=1, 2,…,n)为元素值,n为样品数。将上式两边求对数得到:
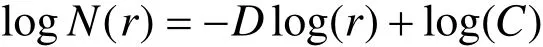
图3 元素lg(r)—lgN(r)图
对元素的原始数据进行统计,用求得的logN(r)和log(r)投绘散点图,采用最小二乘法对其进行分段拟合,求出两段线性方程;通过距离剩余平方和(E)最小的方法对分段方程进行约束,并通过显著性检验,以此得到两个分维数(D1、D2)的估计值;两段直线的交点所对应的值(r0)即为异常下限值(T)。
2.3 单元素异常图的圈定
根据上述两种方法求得异常下限值,运用Suffer对原始数据进行克里格插值法进行网格化,采用T,2T,4T,…间隔值绘制等值线,以此圈定研究区单元素异常图(图4)。
3 结论
1)通过统计法和分形—求和法圈定的异常图,均显示出Au、Cu峰值区集中于滩间山群与花岗岩的接触带,及测区内北西向逆断层和北东向破碎带附近,而Bi、W峰值区则与花岗岩关系密切,初步认为Au、Cu具有中低温热液型的富集特征,而Bi、W则呈现出高温型聚集特征。通过对测区内的破碎带进行地表的探槽揭露,已发现多个具有工作价值的较低品位铜矿化带。
2)由于测区内的滩间山群具有分布范围广,Au、Cu背景值相对较高,而Bi、W的背景值相对较低等特点;花岗岩具有分布范围小,Bi、W的背景值相对较高,而Au、Cu背景值相对较低等特征;造成Au、Cu总体背景值较高,频数分布直方图中呈正向偏斜;而Bi、W总体背景值较低,频数分布直方图中则略呈负向偏斜。同时也使得两种方法求得的Au、Cu异常下限值差异较大, 而Bi、W差异较小。
3)传统法是通过模式推算的方法(众值左方的频率分布曲线推算右方曲线)进行计算的,即不考虑元素分布特征引起的偏移,这降低了地质体背景值的差异影响,使得其更加强调主异常区;缺点是减少了弱小异常的显示。分形法的优点在于强调背景区与异常区的识别,但易受低背景区的影响,使求得的异常下限值较低,由于地质体元素分布特征的差异使得分形法扩大了异常范围。
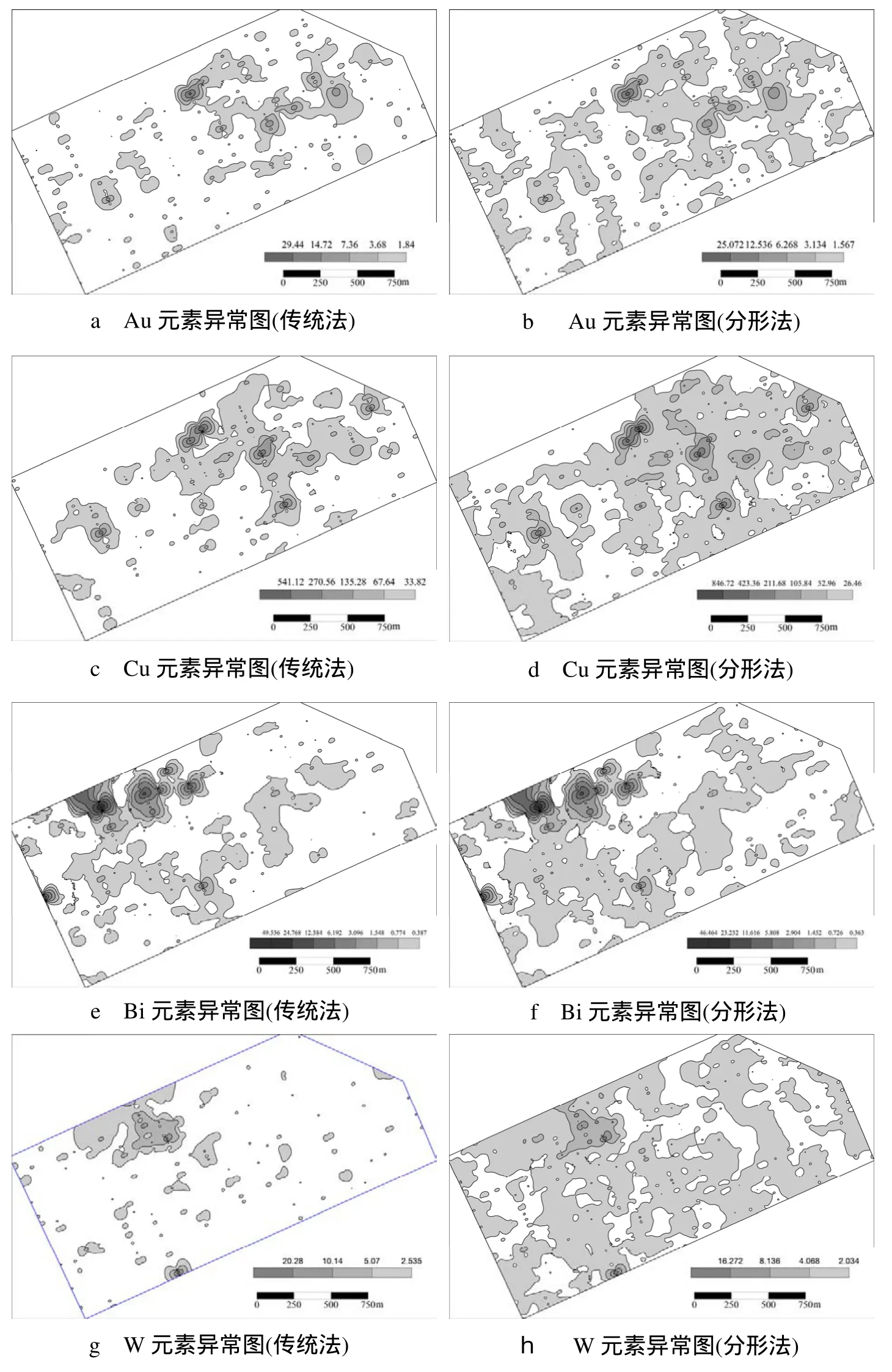
图4 元素异常图
综上,在矿区范围内(面积较小),传统法更加能突出主异常区,屏蔽弱小异常区,该方法在矿山勘查的预、普查阶段工作中,寻求主攻矿体时的作用明显。分形法加强了弱小异常的识别,在矿体外围寻求找矿突破时,由于圈定的异常区不受已知矿体的压制作用,其实用性较强;缺点是受地质体中的背景值分布特征影响较大。
[1] 龚庆杰,张德会,韩东昱.一种确定地球化学异常下限的简便方法[J].地质地球化学,2001,29(3):215~220.
[2] 胡颖. 衬值滤波法在哈尔干查拉铜镍矿化探数据处理中的应用[J].广东化工,2013,40(17):42~43.
[3] 李宾,李随民,等. 地质体方法圈定化探异常—以张家口某地区为例[J].地质找矿论丛,2011,26(2):212~216.
[4] 杨震,梅红波. 基于MAPGIS的含量—面积法确定异常下限—以个旧西区为例[J].物探化探计算技术,2013,35(4);477~480.
[5] Nguyen Tien Thanh,刘修国,等. 基于稳健统计学和EDA技术的地球化学异常下限确定[J].物探化探计算技术,2013,35(3):307~313.
[6] 黄厚辉,郭科,唐菊兴.基于小波多尺度分析的异常下限确定方法[J].地质找矿论丛,2007,22(4):311~313.
[7] 李蒙文,战明国,赵财胜.稳健估计方法在内蒙古新忽热地区水系沉积物测量异常评价中的应用[J].矿床地质,2006(01).
[8] 熊超,葛良全,罗耀耀,谷懿.多种确定地球化学异常下限方法的比较[J].四川有色金属,2012(1):52~55.
[9] 戴慧敏,宫传东,等.区域化探数据处理中几种异常下限确定方法的对比[J].物探与化探,2010,34(6):782~785.
[10] 春乃芽.如何利用Excel处理化探数据[J].物探化探计算技术,2006,28(3):272~276.
[11] 赵君,乔树岩,戴慧敏.水系沉积物测量在阿巴通德拉扎卡地区找矿应用[J].2011,35(1):24~27.
[12 ]成秋明,张生元,左仁广,等.多重分形滤波方法和地球化学信息提取技术研究与进展[J].地学前沿,2009,16(2):185~198.
The Application of Pedogeochemical Survey to Prospecting in the Huangji Gully
WANG Yu LUO Jun-feng XIE Gang
(No.109 Geological Team, BGEEMRSP, Chengdu 610100)
The anomaly thresholds for Au, Cu, Bi, W elements are calculated by means of statistic method and fractal-summation method, and single element anomalies for Au, Cu, Bi, W are delineated on the basis of pedogeochemical survey data. The results indicate that enrichment in Au and Cu is related to fractured zone and Bi-W mineralization is related to granite rock mass.
pedogeochemical survey; threshold; statistical method; fractal-summation method
P632+,1
A
1006-0995(2014)04-0628-04
10.3969/j.issn.1006-0995.2014.04.036
2014-01-013
王玉(1984—),男,安徽人,工程师,研究方向:地质学
