一种基于稳压控制的分布式电源容量确定方法

国网北京市电力公司 师恩洁

国网北京市电力公司 丁冬

专利局专利审查协作北京中心 刘勇

1 引言

本文首先根据接入配电网的分布式电源的V-P关系，确定了过电压是引起一系列问题的根源，然后本文中采用了DG运行在超前功率因数状态下，通过吸收无功功率防止系统过电压，以及消除可能产生的系统波动和电压崩溃。

本文指出在系统负载最小和发电功率最大的情况下，系统过电压最严重。这与传统的负载功率和发电功率之间的关系正好相反[1]。本文提出了一种配电网电压的系统分析方法，提出了一种适于实际应用的分布式电源容量确定方法，使馈线电压和电压波动在可接受的范围内的同时，使接入的多个分布式电源的容量最大，对变电站中的其他设备影响最小。与其他方法相比，本方案简单可靠。

2 电压-功率关系 V-P关系

2.1 传统的配电网V-P关系

一个典型的变电站为12路或者8路馈线，这些馈线辐射到多个配电变压器。许多输电线需要长距离供电，我国多采用35kV以下配电网，典型的10kV输电线输电距离约为10km，输送功率200～300kW典型的20kV输电线输电距离超过20km，输送功率500～800kW。假定最小负载为峰值负载的30%，整个输电线路上的电压值保持在0.94～1.06p.u.[2]。当输电线路上的电压在正常运行范围内时，配电网中的电路元件可以认为线性阻抗元件。因此，在配电网侧V-P关系可以由一个戴维南等效电路来研究。

图1表示在接入DG的配电网戴维南等效电路，V-P关系曲线可以由下面的式1表示。

图2表示传统的没有分布式发电设备，仅有负载接入公共点的典型V-P关系曲线。此时，当负载增加时，由于其功率因数滞后，负载吸收无功，公共点处的电压下降。这种情况下，电压控制非常简单，仅需要馈线功率增加时，保持母线电压不下降即可。实际上，一般含有电容补偿设备的变电站低压侧母线电压一般保持在1.035～1.055p.u.之内。

图1 分布式发电设备戴维南等效电路

但是，当配电网侧接入分布式发电设备，其发电功率超过用电功率时（即，产生了一个反向的潮流），分布式发电设备输出功率增加时，馈线电压增大。由于在最小负载时，典型的馈线电压保持在电压上限下0.005p.u.，因此可以接入的DG将非常有限。但是不能为了能够使馈线接入更多的DG，而降低变电站低压侧母线电压，因为其他很多出线侧没有接入DG，他们与接入DG的馈线接在相同的变电站母线上[3-4]。

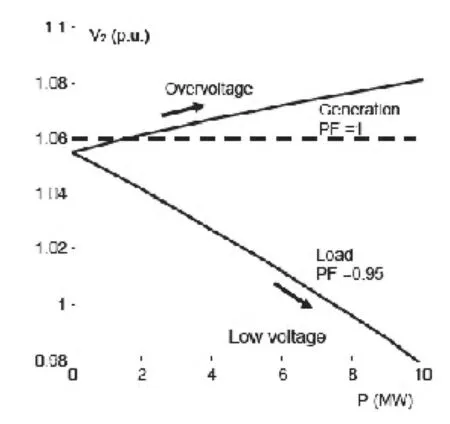
图2 传统输电线路V-P关系曲线

为了在最小负载工况下接入更多的DG而不至于使电压越限，分布式发电设备需要在超前功率因数下运行，即吸收无功，保持电压稳定[5-6]。但是这样的运行方式容易产生电压跌落和比较大的电压波动，下面的部分重点介绍这部分内容。

2.2 DG在单位功率因数下运行

一般分布式电源多为电力电子接口的发电设备，其多采用固定功率因数运行[3]。公式1中的V-P关系与传统输电系统中的关系类似，但是有两点不同。首先，配电网络中电抗与电阻的比例范围在1～5之间，但是在高压输电系统中，这个比例高达10～30。因此，在分析电压问题时，高压输电系统中的经常被忽视的电阻分量在配电系统中不能忽略。其次，配单网多为辐射型，其比输电网络相比更脆弱，因此配电网与DG的公共节点处的电压受DG输出功率影响很大[4]。这两个难题是含有DG配电网很难保持电压稳定的主要原因。

图3表示在距离35kV变电站20km的公共节点处的P-V曲线，假设变电站的容量为800MVA。由图3可以看出，单位功率运行时，PCC处的电压随着功率增加到一定值后开始下降，电压的变化可以由式(2)表示。其中下标0表示运行点。

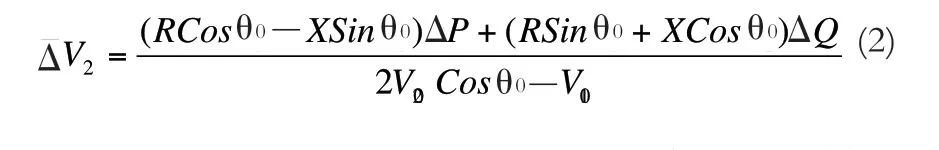
等式表示了PCC处电压与注入功率的关系，在单位功率因数下，注入无功ΔQ为0，电压变化仅仅与输入有功功率ΔP相关。在配网中θ0很小，因此为数，恒定功率P下，等效阻抗中电阻的比例越大，电压变化越快。当时，运行电压达到最大值。

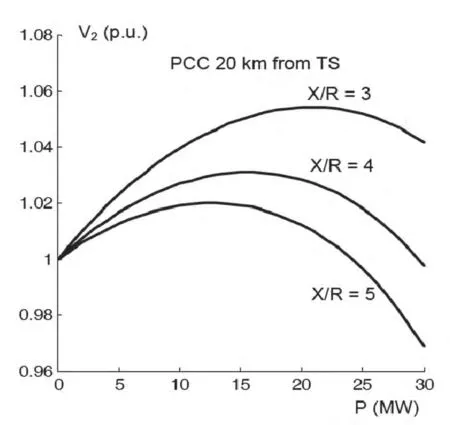
图3 单位功率因数运行DG的PCC处V-P关系曲线

2.3 DG非单位功率因数运行

在图3中，DG的戴维南等效电路的开路电压V1被设置是为1p.u.，实际配电系统中的V1在1.035～1.055p.u.之间，由此可见，图2表示了在DG运行在单位功率因数时，母线电压很容易产生过电压问题。因而，在许多情况下，分布式电源必须工作在超前功率因数运行方式，来避免系统过电压。

由公式2可知，在DG不在单位功率因数下运行时，ΔQ不再是0，PCC处的电压与ΔQ和ΔP均相关。当功率角θ0为正时，由于因此PCC处的电压对ΔQ更加敏感。功率因数的一个轻微变化会引起ΔQ的巨大变化，因此严重影响到PCC处的电压水平。

图4表示了DG工作在不同的功率因数下V-P关系。由图可以看出，DG可以工作在超前功率因数的模式下，来避免系统过电压，但是这种工作模式可能导致系统电压过低，或者电压不稳定。

图4 功率因数不同时PCC处V-P关系曲线

3 其他影响PCC处电压的因素

3.1 负荷水平对PCC处电压的影响

图5表示了在负荷水平PL=0、PL=2.5MW和PL=5.0MW时的V-P曲线图，其中蓝线表示单位功率因数运行下的电压变化，红线表示功率因数为-0.99时的电压变化。

由图5可以看出：1、DG滞后功率因数运行时，负荷增加PCC处下降；2、当DG以较大的功率因数运行时，PCC处的电压会随着DG功率增大升高到一个高点；3、当DG超前功率因数运行时，DG输出功率增加引起的电压下降与负荷增加引起的电压下降叠加在一起；4、最大电压点与分布式电源的功率因数有关。

由于DG输出功率增加引起的电压下降与负荷增加引起的电压下降叠加在一起，因此DG运行工况下的功率因数必须慎重选择。

3.2 变电站短路容量的影响

在高压输电系统中，线路主要是感性的，阻性分量可以本忽略。但是当变电站短路容量较小时，在PCC处较小的X/R就会对系统电压产生更大的影响。图6所示的系统中变电站短路容量减少为200MVA，其余参数与图5中的相同，图中可以看出，当DG以超前功率因数运行时，其输出容量不足20MW时便出现了电压跌落现象。

图5 DG单位功率因数和非单位功率因数运行下V-P关系曲线（其中X/R=4.0）

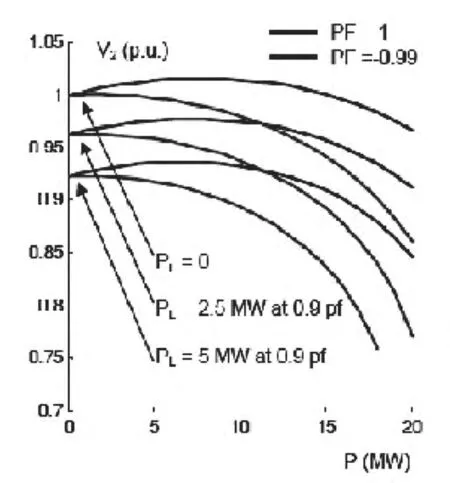
图6 配电网不同负荷水平下PCC处V-P曲线关系(其中变电站短路容量200MVA)

4 电压管理的方法

在接入DG的配电网中，尽管IEEE1547标准[7]建议DG不要主动改变PCC处的电压，但由于大容量的DG接入产生了电压波动问题，因此需要采取合适的电压管理措施。例如，当DG对下级电压进行主动调节，可能导致上级配电网不能根据负载的变化进行主动控制。如前所述，为了避免系统电压跌落，DG应该采用接近单位功率因数运行；为了防止系统过电压，DG应该采用超前功率因数运行，为了保持二者的平衡，同时保证系统接入的DG容量最大，应该采取以下方法。

1）接入配电网的所有DG应该进行固定功率因数运行，通过对配电系统的分析，确定一个合理的功率因数值。

2）所有接入配电网的DG容量应小于变电站短路容量的20%。

3）当接入配电网馈线的DG固定功率因数运行时，馈线电压上升应小于3%。

4）当DG超前功率因数运行时，其吸收无功功率，其功率因数应该不大于0.95。

为了限制短期的电压波动、功率波动和过电压问题，通过测量PCC处的V-P曲线来确定合适的DG输出功率水平，进而确定其运行状态下的功率因数。

5 结论

通过比较PCC处V-P关系曲线，本文分析了影响配电网馈线电压水平的主要因素。然而配电网接入DG以后，为了解决馈线过电压问题而采取的一些措施，容易引起电压跌落和波动。本文系统分析了影响母线电压的因素，给出了在保持电压在合格的要求下，使接入DG容量最大的方法。

1）DG单位功率因数运行时，由于配电网馈线的电抗与电阻之比较低，PCC处电压迅速增加，引起系统的不稳定；

2）当DG采用超前功率因数运行时，可以在一定程度上避免PCC处的过电压，但是当接入DG容量过大时，当负载增加引起的系统电压降低时，存在系统电压崩溃的危险；

3）为了解决电压崩溃问题，可以采用V-P分析的方法确定PCC处电压在正常范围内时，DG需要的最佳运行功率因数；

4）所有接入配电网的DG容量应小于变电站短路容量的20%，当DG超前功率因数运行时，其功率因数应该不大于0.95。

[1]Masters,C.L,Voltage rise: the big issue when connecting embedded generation to long 11kV overheadlines, Power engineering Journal Vol.16 Issue 2002.(1), pp.5-12 .

[2]Trichakis,P;Taylor, P.C; Lyons,P.F; Predicting the technical impacts of high levels of small-scale embedded generators on lowvoltage networks, Renewable Power Generation,IET,Vol. 2, 2008 (4),pp.249-262

[3]Viavan,F.A.,Karlsson,D.,Voltage and Reactive Power control in systems with Synchronous Machine-Based Distributed Generation. Power Delivery IEEE Transactions on Vol. 23, 2008 (2)，pp.1079-1087.

[4]李晶.分布式发电系统并网逆变器的无功控制策略[J].电力系统及其自动化学报,2011,01:155-159.

[5]Ayres, H.M.; Freitas, W.; De Almeida, M.C.; Method for determining the maximum allowable penetration level of distributed generation without steady-state voltage violations, Generation, Transmission & Distribution, IET, Vol. 4, 2010 (4),pp.495-508.

[6]钟嘉庆,叶治格,卢志刚.分布式发电注入容量与接入位置的优化配置分析[J]. 电力系统保护与控制,2012,07:50-55.

[7]IEEE Std 1547TM-2003, Standard for Interconnecting Distributed Resources with Electric Power Systems.