基于个性化脉搏波传导参数的连续血压测量方法研究

董骁，宾光宇，吴水才

北京工业大学 生命科学与生物工程学院 ,北京 100124

基于个性化脉搏波传导参数的连续血压测量方法研究

董骁，宾光宇，吴水才

北京工业大学 生命科学与生物工程学院 ,北京 100124

目的 建立基于个性化脉搏波传导参数的连续血压测量方法模型。方法 对18名受试者进行了运动实验，在运动实验过程中连续记录受试者的心电和手指容积脉搏波，同时利用动态血压计每2 min采集受试者的血压；每个受试者间隔1周的时间进行第二次实验；采用最小均方误差线性估计的方法来建立脉搏波传导时间和收缩压之间的线性模型。结果 同一个受试者脉搏波传导时间与收缩压具有良好的线性关系（r2=0.91±0.06），线性模型的检测误差为（3.48±1.69）mmHg，且具有较好的稳定性。但对于不同受试者，很难建立统一的线性模型（r2=0.14）。结论 基于个性化脉搏波传导参数的连续血压测量方法是可行的，有望实现无袖带的连续血压测量。

动脉压；脉搏波；传导参数；收缩压

0 前言

动脉压（ABP）是反映人体循环机能的重要生理参数，同时也是临床上诊断疾病、观察治疗效果、进行预后判断的重要依据[1-3]。动脉压测量的方法有两大类，即直接测量法和间接测量法[4]。直接测量法即在动脉腔内置管测量内压力，一直被认作是临床血压测量的“金标准”[5]。间接测量法即无创测量，分为间断和连续两类。传统的间断测量方法有示波法和柯式音法。无创连续血压测量相对有创测量具有测量方便、病人无创伤等优点[6]；同时相对于间断测量法，连续测量可以监控每个心动周期内的血压变化，因此无创连续血压测量在临床血压监测、家庭监护及预警以及降压药的监测上具有十分重要的意义[7-8]。

无创连续测量方法主要有恒定容积法、张力测定法等，但由于这些方法操作复杂[9]，仍然没有摆脱袖带充气的测量模式，因此不适合于长时间连续血压监控。近些年脉搏波传导时间（PWTT）或传导速度（PWV）测量法逐渐成为重点研究方向。PWTT即动脉脉搏波从主动脉瓣传播到末梢所需要的时间[10]，通常为心电R波波峰点到脉搏波信号的特征点。PWV即脉搏波在动脉中的传播速度。

早在19世纪就有学者提出了PWV与ABP之间的数学基础模型[11]，但直到20世纪70年代，Gribbin等才成功地利用PWV跟踪血压的变化，但不能得到精确的血压值[12]。之后，有学者的实验也充分证实了血压与PWTT之间具有紧密的联系[13]，许多研究都验证收缩压与PWTT呈线性相关[14-15]，而舒张压和平均压与PWTT的关系并不大，需要再通过其他方法进行间接推算。经过进一步研究PWTT与血压的相关性，有学者发现PWV与PWTT除了受到动脉压影响外，还取决于动脉管壁弹性、血液密度、粘度等多种因素[16-17]。现有研究大多采用对不同受试者建立统一模型的处理方法，希望模型能够适用于所有的受试者，并没有对每个受试者进行个性化参数订制。有文献结果甚至显示动脉压与PWV呈良好的非线性关系。目前许多研究中建立的模型并不是非常稳定的，同时不同使用者利用统一模型测得的血压值也不是很准确。为进一步提高血压的计算精度，降低个体差异的影响，本研究在处理数据过程中对每个受试者单独建立血压-参数模型，并对模型稳定性进行验证。

本研究邀请18名受试者参与运动实验，使用动态血压计和自主研发的心电、脉搏波采集装置以及采集软件来获取受试者在运动过程中的心电、脉搏波和血压。由于舒张压和平均压与PWTT的相关性并不大，本文只针对收缩压进行相关性建模。利用matlab软件分别对每一受试者的数据进行线性回归处理，再对全部受试者的实验数据进行线性回归分析，建立数学模型，对两种模型验证结果进行比较。同时对每一受试者的单个模型稳定性进行检验，检测误差大小，确定个性化参数订制是否可行。

1 实验方法与数据分析

1.1 实验方法

实验需要受试者一段时间内在实验室的动感单车上间断蹬车/静止。共邀请了18名受试者，10名女性，8名男性，年龄均在22～26岁。每名受试者均需完成两次运动实验，实验过程相同，间隔时间为1周，完成单次实验大约需要1 h。

实验过程如下：

（1）将心电电极贴分别贴在左侧锁骨正中以下3 cm处以及左侧最后一根肋骨的正中。将指夹式脉搏波采集器夹在右手中指，两路信号线连接在自主研发的心电脉搏采集电路板后固定在受试者的身体上，动态血压计绑在左大臂上。

（2）在受试者静止状态下开始同时采集心电与脉搏波的数据，采样频率为500 Hz。待接收到的心电信号和脉搏波信号均稳定正常，开始正式保存数据。

（3）从第一次测量血压开始，每隔2 min测量一次血压，每次大约需要1 min得到血压值，测量血压的时间段利用计算机采集软件进行标记。在进行3次静止状态下的血压测量操作后，受试者开始蹬车，总共蹬车时间为10 min。结束蹬车后，继续每隔 2 min测量一次血压，直至记录到的血压值与平稳时的血压值相近为止。

（4）实验结束后，实验者应记录好12～14组该受试者的收缩压、舒张压和心率，以及全部心电脉搏波信号。心电脉搏波信号有相对应的12～14个测量血压的时间段标记。

（5）间隔一周后进行第二次实验，重复上述实验步骤。

1.2 数据分析

每一位受试者每次实验能够采集12～14组血压数据，标记为SBPi,j(n)， 其中i=1,2,..18，代表受试者的序号；j=1,2，代表实验的次数；n代表血压测量的序号。

选取血压测量时的心电和脉搏波数据计算PWTT。在PWTT的计算过程中，选取心电信号QRS波的R波峰值点作为计算起点，脉搏波信号主波峰上升沿最大斜率点作为终点。每次血压测量大约持续40 s ，能够获得多个心跳周期，对其进行平均，作为该次血压对应的脉搏波传导时间PWTTi,j(n)。

由于PWTT和收缩压之间为线性关系，因此本文采用最小均方误差线性估计的方法来建立PWTT和收缩压之间的线性模型。其模型公式如下：

SBP=b1+b2×PWTT (1)

其中SBP为收缩压，PWTT为脉搏波传导时间，b1和b2为模型中的待定参数，进行个性化参数订制时，每位受试者的b1、b2不同。采用r2来衡量两者的线性程度，用误差E来表示最终估计的准确性。

本文进行了如下3个方面的分析：

（1）对第一次实验的所有受试者的数据进行线性模型估计，获得其r2和E。

（2）对第一次实验的单个受试者进行模型估计，获得每一个受试者的个性化模型以及相对应的r2(n)和E(n)。

（3）利用第一次实验获得的线性模型来检验第二次实验的数据，获得其误差E(n)。

2 实验结果

实验过程中，动态血压计测量收缩压数值比较准确，以500 Hz采样频率采集的心电和脉搏波信号也具有很强的完整性，基于matlab的算法对特征点的检测准确率很高，因此为通过线性回归处理建立数学模型提供了良好的基础，能够比较出个性化的参数模型与普适参数模型的优劣。

表1为对第一次实验数据进行线性模型估计后得到的每一受试者个性化模型相对应的r2(n)和E(n)，以及所有受试者统一模型的r2和E。18名受试者的实验数据经过编号、线性回归、计算误差等一系列处理后，得到相关系数以及平均误差。将18名受试者的实验数据集合到一起进行线性回归处理，得到全部数据的相关系数和平均误差。如表1所示，将所有受试者数据分别通过线性回归建立的个性化模型相关系数基本在0.9左右，而相关系数越大说明回归方程越显著，同时误差平均值仅为（3.48±1.69）mmHg，说明针对每一个受试者个体，PWTT与收缩压具有良好的线性关系。图1为全部受试者数据整合后的散点图，图中斜线为对全部受试者数据进行线性回归操作得到的PWTT与收缩压的普适模型，将全部数据整合后进行线性回归操作建立的普适模型的相关系数r2仅为0.14，而误差平均值达到了16.74 mmHg，说明全部数据的PWTT与收缩压线性关系很差。不同受试者的数据采用不同形状的点加以区分，可以明显看到每一受试者各自的数据中PWTT与收缩压都具有很好的线性关系，但每个受试者由于个体的不同使得他们之间的线性模型差异非常大。针对单个使用者建立的个性化参数模型要远远优于针对所有使用者建立的普适模型。

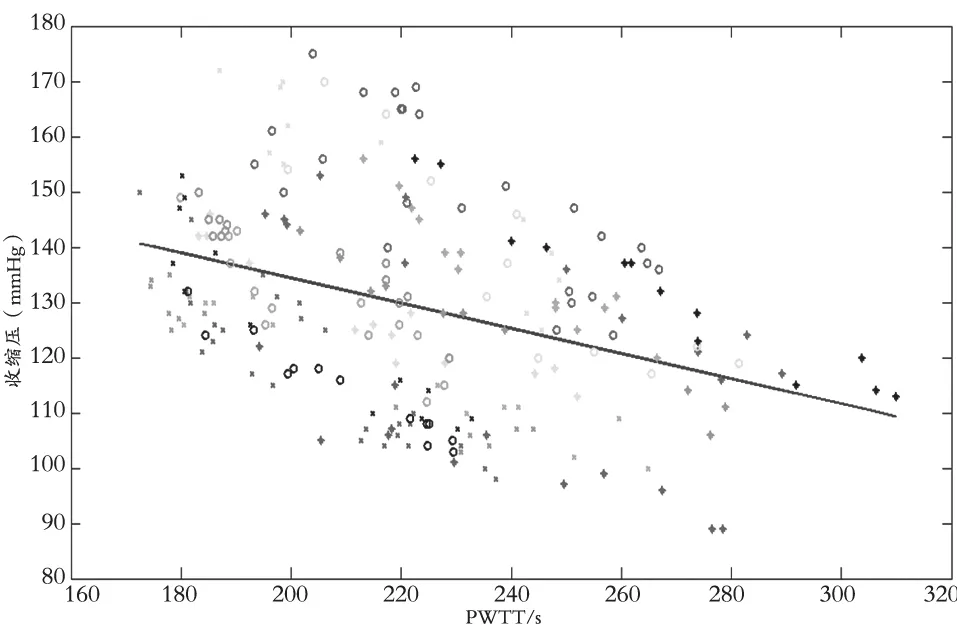
图1 18名受试者数据的散点图

表2为利用第一次实验获得的线性模型来检验第二次实验的数据，获得的误差E(n)。将18名受试者第二次实验的数据经过编号、代入模型、计算误差等一系列处理后，得到平均误差。全部18个误差的平均值为（7.49±2.87）mmHg，误差较小，证明在不同时间下，针对每位受试者的PWTT-血压线性模型具有很好的稳定性。

综合第一次实验数据的建模结果与第二次实验的检验结果，可以得出：在利用PWTT推算血压的过程中，单一受试者的PWTT与收缩压具有良好的线性关系，18名受试者模型的相关系数基本＞0.9，而第一次实验数据的误差平均值也只有（3.48±1.69）mmHg。利用该模型检验第二次实验数据的误差为（7.49±2.87）mmHg，＜10 mmHg，可以满足临床应用的需要，说明该模型具有很好的稳定性。对比不同受试者间的线性模型参数和散点图，可以发现不同受试者间的个性化模型具有很大差异。将第一次实验的全部数据整合后进行线性回归，其相关系数r2仅为0.14，而误差平均值＞16 mmHg,证明针对不同受试者建立个性化参数订制模型准确率要远远好于建立一个普适模型。

表1 第一次实验的相关系数与平均误差

表2 模型检验第二次实验数据的平均误差

3 讨论与结论

现有研究表明，PWTT与血压之间有着很大的联系，可建立血压-脉搏波传导参数的数学模型，用于检测血压[18]，然而这些研究都希望建立一个可适应于所有使用者的脉搏波传导参数与动脉压的关系模型，但这些方法获得的模型没有一个统一的标准。有文献指出，脉搏波传导参数与血压之间为非线性关系，并建立了相关模型，但结果显示该模型检测血压误差较大，不能满足临床要求[18]。

本研究在采用PWTT作为传导参数的基础上，提出针对每一位受试者建立个性化参数订制模型，以提高脉搏波传导参数推算血压的精确度。通过比较不同受试者的线性模型以及普适模型，发现不同受试者之间的模型存在很大差异，每名受试者的个性化参数模型精确度要远远高于针对所有受试者建立的普适模型；同时经不同时间采集的数据检验，个性化参数模型也具有很好的稳定性。

[1] 徐克,周奇,韦云隆.无创血压测量[J].重庆工学院学报,2008, 22(1):164-167.

[2] 胡文志,周海波.监护仪在心房纤颤病人血压测量中的准确性评价[J].中国医疗设备,2014,29(4):120-122．

[3] 李顶立.基于脉搏波的无创血压测量方法研究[D].杭州:浙江大学,2008.

[4] 齐颁扬.医学仪器(上)[M].北京:高等教育出版社,1996.

[5] 李桥.利用脉搏波传播时间计算动脉血压的研究[J].中国生物医学工程学报,2011,30(4):509-513.

[6] 樊海涛,叶学松,段会龙.无创血压检测技术[J].中国医疗器械信息,2004,10(5):53-56.

[7] Kikuya M,Hozawa A,Ohokubo T,et al.Prognostic significance of blood pressure and heart rate variabilitier: the ohasama study[J]. Hypertension,2000,36(5):901-906．

[8] Rhee S,Yang BH,Asada HH.Artifact-resistant power-efficient design of finger-ring plethysmographic sensors[J].IEEE Trans Biomed Eng,2001,48(7):795-805.

[9] Climie RE,Schultz MG,Nikolic SB,et al.Fell and James E. Sharman. Validity and reliability of central blood pressure estimated by upper arm oscillometric cuff pressure[J].Am J Hypertens,2012,25(4):414-420.

[10] Teawoo N,Jongman C,Junho P,et al.A coronary pulse wave velocity measurement system[C].Conf Proc IEEE Eng Med Biol Soc,2007.

[11] Maguire M,Ward T,Markham C,et al.A comparative study in the use of brachial photoplethysmography and the QRS complex as timing references in determination of pulse transit time[C]. Engineering in Medicine and Biology Society,Proceedings of the 23rd Annual International Conference of the IEEE,2001.

[12] 于潇,林君,李肃义.无创血压测量技术的发展概况[J].广东医学,2012,33(15):2356-2359.

[13] Zakaria NA,Sharifmuddin NB,Wanmohd WMF,et al.Pulse wave transit time and its relationship with systolic blood pressure[C].6thWorld Congress of Biomechanics(WCB 2010),2010.

[14] Payne RA,Syemonides CN,Webb DJ,et al.Pulse transit time measured from the ECG:an unreliable marker of beat-to-beat blood pressure[J].Appl Physiol,2006,100(1):136-141.

[15] 孟祥平,刘兵,邓宝芸,等.利用脉搏波传播时间计算动脉血压的研究[J].中国生物医学工程学报,2011,30(4):509-513.

[16] 王炳和,杨颙,相敬林.一种无创测定桡动脉脉搏波速度的方法及影响脉搏波速度的因素[J].生物医学工程学杂志,2000, 17(2):179-182.

[17] 陆渭明,李和平,蒋正尧,等.对利用脉搏波传播速度间接测量血压时主要影响因素的研究[J].中国生物医学工程学报, 1995,14(1):88-93.

[18] Gesche H,Grosskurth D,Küchler G,et al.Continuous blood pressure measurement by using the pulse transit time:comparison to a cuff-based method[J].Eur J Appl Physiol,2012,112(1):309-315.

Research on the Continuous Blood Pressure Measurement Method Based on Personalized Pulse Wave Transmission Parameters

DONG Xiao, BIN Guang-yu, WU Shui-cai
School of Life Science and Bioengineering, Beijing University of Technology, Beijing 100124, China

Objective To establish a continuous blood pressure measurement model based on personalized pulse wave transmission parameters. Methods ECG parameters and fi nger pulse waves of 18 subjects were continuously measured and recorded in exercise tests and their blood pressures (BP) were also recorded every 2 minutes with dynamic BP monitor. The exercise tests of all the 18 subjects were conducted repeatedly one week later. A linear model between pulse wave translation time (PWTT) and systolic blood pressure (SBP) was constituted through linear minimum mean square error estimation. Results There is a good linear relationship between PWTT and SBP of the same subject (r2=0.91±0.06) and the test error of the linear model with nice stability is (3.48±1.69) mmHg. However, it is very diff i cult to build a unif i ed linear model for all subjects (r2=0.14). Conclusion It is feasible to measure blood pressure continuously based on personalized pulse wave transmission parameters, which can contribute to the realization of sleeveless continuous blood pressure measurement.

arterial blood pressure; pulse wave; transmission parameters; systolic blood pressure

TN911.7

A

10.3969/j.issn.1674-1633.2014.10.007

1674-1633(2014)10-0024-04

2014-05-20

国家自然科学基金项目资助（61105123）。

宾光宇，硕士研究生导师。

通讯作者邮箱：guangyubin@gmail.com