一种改进的小波阈值算法在激光侦听中的应用
2014-06-23张伯虎
屈 直,张伯虎
一种改进的小波阈值算法在激光侦听中的应用
屈 直1,张伯虎2*
(1.中国人民武装警察部队工程大学研究生管理大队,西安710086;2.中国人民武装警察部队工程大学信息工程系,西安710086)
为了更好地实现激光侦听中的语音降噪,采用一种改进的小波阈值去噪算法,进行了理论分析和实验验证,取得了一系列仿真数据。结果表明,改进后的算法与传统的降噪算法相比,降噪后的语音信噪比显著提高,降噪效果明显,信号波形更加平滑、失真度小。
激光技术;去噪;小波阈值算法;仿真
引 言
语言对话是信息传递最直接、有效的方式,对被关注对象谈话内容的侦听是刑侦部门十分关注的话题,激光侦听因其非接触性、隐蔽性和抗干扰新性强等特点,一直作为获取情报的重要手段,但激光侦听信号中包含的噪声很多,语音降噪的好坏将直接影响侦听效果和侦听设备的使用范围。传统的降噪方法中,维纳滤波对信号的平稳性要求较高;谱减法适用的信噪比范围窄,而且会产生音乐噪声;最小均方误差估计(minimum mean-square error estimation,MMSE)算法运算量大、实时性不好。由于激光侦听对实时性的要求很高,所以上述算法都不适合处理激光侦听信号。对此,本文中提出了一种改进的小波阈值去噪算法,并进行了仿真处理。仿真结果表明,改进后的算法与传统的降噪算法相比,降噪后的语音信噪比显著提高,降噪效果明显、失真度小,有利于扩大激光侦听的使用范围。
阈值函数法又称小波阈值去噪法,是目前研究和应用广泛的去噪方法之一。DONOHO等人已经证明:小波阈值去噪法的降噪效果明显优于其它的经典去噪方法。该方法的理论基础是:带噪语音信号经过小波变换后,随尺度的增大,实际信号的小波系数增大,而噪声所对应的小波系数减小,由此可知,通过一个阈值函数并设置一个合理的阈值,就可以滤除噪声,最后对估计系数进行小波逆变换,就可获得去噪后的语音信号。但当信噪比比较低时,容易将原信号的高频部分当做噪声滤除掉。小波系数的筛选主要依赖于阈值函数和阈值,它是阈值函数法的关键步骤。当然选用的阈值函数不同,降噪效果也会不同[1]。
1 小波阈值去噪原理与步骤
对于语音信号的去噪,假定其含噪信号模型可以表示为:

式中,f(n)为真实语音信号,s(n)为含有噪声的信号,e(n)是一个标准的高斯白噪声,ei(n)~N(0,1),σ是噪声系数,N为离散采样序列x(n)的长度。
阈值去噪法的基本原理可以概括为:带噪语音信号中的语音成分在小波域的能量相对集中,其分解后的小波系数的绝对值比较大,而噪声信号分解后的小波系数的绝对值比较小,因此,只要设置一个合适的阈值,并将小于阈值的小波系数置零,就可以将噪声滤除,达到降噪的效果[2]。
假设s(n)是一个叠加了高斯白噪声的有限长带噪信号,其去噪步骤为:(1)分解过程。选定一种小波,对含噪声信号s(n)进行N层分解,得到相应的小波系数;(2)作用阈值过程。对分解后得到的各层小波系数Wj,k选择一个阈值,并采用阈值函数对系数进行处理;(3)重建过程。降噪处理后的小波系数经小波逆变换,得到去噪后的原始语音信号[3]。
2 常用阈值函数
信号小波分解后的小波系数设为Wj,k,阈值函数得到的小波系数估计值用为W^j,k,λ为阈值。常用的阈值函数如下[4]所示。
(1)硬阈值函数:

(2)式为硬阈值函数的数学表达式,由公式可以看出,硬阈值函数对小波系数作如下处理:将绝对值小于阈值的小波系数置零,绝对值不小于阈值的小波系数则保持不变[5]。
(2)软阈值函数:
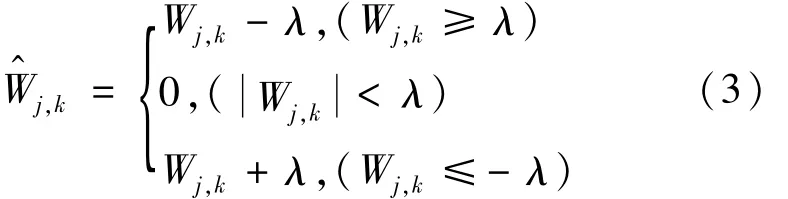

Fig.1 Hard-threshold function and soft-threshold function
(3)式为软阈值函数的数学表达式,由公式可以看出,软阈值函数对小波系数作如下处理:对绝对值小于阈值的小波系数置零,而对绝对值大于等于阈值的小波系数进行收缩处理。硬阈值函数与软阈值函数如图1所示,其中实线为硬阈值函数,虚线为软阈值函数[6],横坐标表示信号的原始小波系数,纵坐标表示阈值化后的小波系数。
3 改进的阈值函数
硬阈值函数和软阈值函数是小波阈值去噪算法中最常用的两种阈值函数。由于降噪效果较好,这两种算法已经被广泛应用于语音降噪领域,但它们本身存在着一些缺点。
硬阈值法主要有以下3个缺点:(1)小波系数估计值在经硬阈值函数处理后,在±λ处不连续,因此利用重构所得的信号有可能会出现振荡;(2)硬阈值法只对绝对值小于阈值的小波系数进行处理,对绝对值大于阈值的小波系数则不做任何处理,因此,小波系数比较大的脉冲噪声将继续保留在信号中;(3)硬阈值法在一些地方会产生突变,使处理后的语音信号会伴有音乐噪声[7]。
经过软阈值方法处理后的小波系数估计值虽然整体连续性好,降噪效果相对平滑,但是当≥λ时,小波估计系数与含噪声信号的小波系数之间一定会存在固定的偏差,这与噪声分量随着小波系数的增大而减小的趋势不相符合,直接影响到重构信号与真实信号的逼近程度,势必会给重构信号带来误差,从而降低语音的清晰度[8]。
当<λ时,硬、软阈值函数都将置零,因而小波系数较小的有用信号也会被当作噪声滤除掉。
为了克服硬、软阈值函数的缺点,作者设计了一种改进的阈值函数。通过观察,软、硬阈值函数都是单调递增的奇函数,软阈值函数的去噪效果和性能比硬阈值函数的要好。因此,构造的改进的阈值函数在满足上述两个要求的前提下,还应尽量吸取软阈值函数的优点。利用指数函数构建的改进的阈值函数如下:

式中,c>0为一待求常数。当x→+∞时,φc(x,λ)≈x-λ;当x=0时,φc(x,λ)=0;当x→-∞时,φc(x,λ)≈x+λ;这和软阈值函数趋势相符。令x=-x,代入(4)式得:
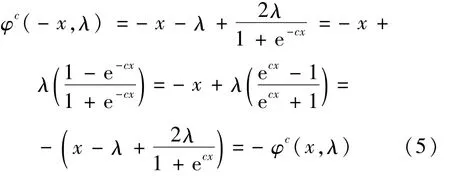
因此,改进的阈值函数是奇函数,关于原点对称,故只需分析(0,+∞)区间即可。
首先,函数φc(x,λ)在(-∞,+∞)应满足单调递增这一条件,则有:

对(4)式求偏导,并代入(6)式得:
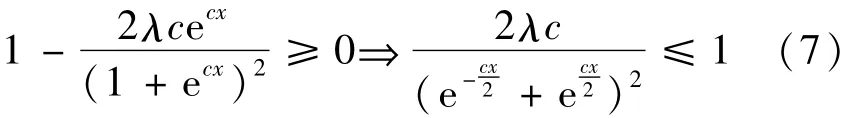
由于

所以,

当c≤2/λ时,新的阈值函数φc(x,λ)在(-∞,+∞)单调递增。
其次,为了使改进的阈值函数和软阈值函数尽可能相似,充分利用软阈值函数的优点,令δ(c)为改进的阈值函数和软阈值函数的差值函数,则η(c)能取得最小值。
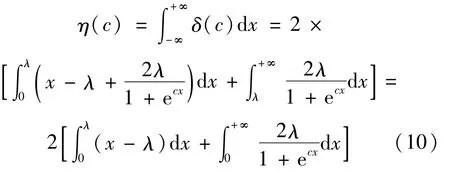
令u=ecx,并代入(10)式得:
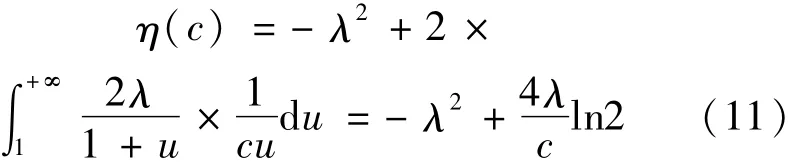
由数学知识可知,当η(c)为开口向上的二次函数时,才可能取得最小值。当c≤(4ln2)/λ时,η(c)存在最小值。
综合以上两个条件,取c=2/λ,并代入(4)式,得到改进的阈值函数如下:

改进的阈值函数和硬、软阈值函数如图2所示。实线为改进的阈值函数,虚线为硬阈值函数和软阈值函数。
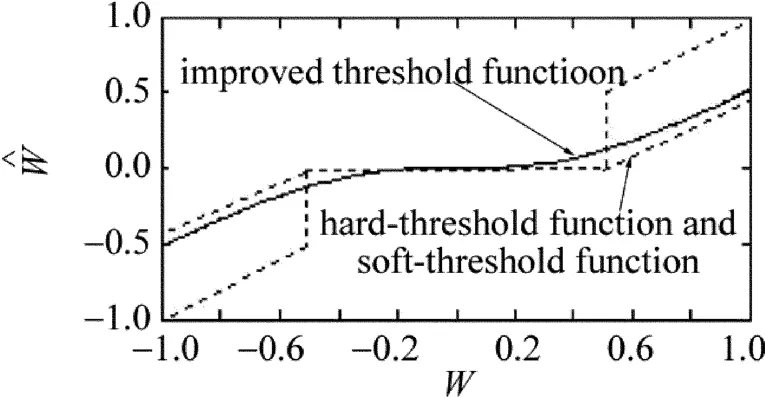
Fig.2 Threshold function
从图2中可以看出,改进的阈值函数处于硬、软阈值函数之间,是一条单调递增的平滑曲线,没有间断点,因而不会产生振荡。改进的阈值函数对所有的小波系数都进行处理,克服了硬、软阈值函数在小波系数比较小时置零的缺点,提高了小信号不被滤除的可能性;同时,它克服了软阈值函数存在恒定偏差这一缺点,符合噪声系数的客观规律;对绝对值大于阈值的系数进行与软阈值函数相同的收缩处理,理论上应用前景很好[9]。
4 阈值的选取规则
阈值的选取是小波阈值去噪算法中的关键因素。主要由噪声方差的估计值和子带系数的能量分布确定确定阈值,因为噪声是随机的,所以对阈值进行估计在去噪过程中是必须首先做的。比较著名的阈值估计法有:SUREShrink阈值法、VisuShrink阈值法、Minimaxi阈值法和HeurSure阈值法等[10]。
VisuShrink阈值法中阈值统一定义为λ=σn×其中,σn为噪声的标准差,N为信号的长度。
SUREShrink阈值确定过程为:对于给定的阈值λ,首先得到它的似然估计,然后将似然函数最小化,得到所需要的阈值[11]。
HeurSure阈值法中阈值由下式确定:

式中,λ1为统一阈值;λ2为SURE阈值;η=;wk为小波去噪后的语音信号。
Minimaxi阈值则由下式确定:

5 仿真实验及结果分析
在本节的仿真图形中,横坐标均为语音信号的采样时间(单位为s),纵坐标均为语音信号的幅度。
5.1不同阈值函数的去噪效果分析
为了说明改进的阈值去噪函数的降噪效果比传统的硬、软阈值函数的去噪效果好,进行如下的语音去噪对比试验。实验中采集的原始语音信号为“陕西省西安市”,采集软件为WINDOWS自带的录音机,采样频率为8kHz,数据长度为16位,采样点数为112000,为单声道采样,音频文件以wav格式保存。添加的噪声特性为加性高斯白噪声,将原始语音信号与不同强度的白噪声进行混合,从而产生带噪语音信号。采用sym8小波基对带噪的语音信号进行处理,然后进行6层分解,选取阈值为统一阈值,分别用硬阈值函数、软阈值函数和改进后的阈值函数进行去噪实验。原始语音信号波形如图3所示[12]。

Fig.3 The original speech signal waveform

Fig.4 The denoised speech signal waveform using different threshold function(Rin=20dB)
(1)输入信噪比为Rin=20dB时。分别采用不同阈值函数对语音去噪,波形如图4所示。
(2)输入信噪比为Rin=10dB时。采用不同阈值函数对语音信号去噪,波形如图5所示。
(3)输入信噪比为Rin=5dB时。采用不同阈值函数对语音信号去噪,波形如图6所示。

Fig.6 The denoised speech signal waveform using different threshold function(Rin=5dB)
(4)输入信噪比为Rin=0dB时。采用不同阈值函数对语音信号去噪,波形如图7所示。
表1中为采用不同阈值函数去噪后的信噪比。

Table 1 Signal-to-noise ratio using different threshold function
从图3到图7可以看出:与硬、软阈值函数相比,去噪后的语音波形说明了本文中改进算法的去噪效果明显优于前者。特别是当噪声比较大时,经过新的阈值函数去噪后,基本上无失真地恢复出了语音波形;而硬、软阈值去噪后恢复的波形已经产生了畸变,失真现象明显。从表1可以看出:当信噪比比较大时,也就是语音信号和噪声信号区分比较明显时,比较硬阈值函数、软阈值函数和改进后的算法,发现去噪后的信噪比差别不大;但当信噪比比较小时,本文中的改进算法明显优于硬、软阈值法。因此,本文中的改进算法在去噪后波形和信噪比两个指标上都要好于传统的硬、软阈值法,证明了本文中改进的算法是合理的[13]。

Fig.7 The denoised speech signal waveform using different threshold function(Rin=0dB)
5.2改进阈值去噪算法与传统去噪算法的性能比较
为了验证改进阈值去噪算法的性能,分别对自己录制的两段语音信号进行如下处理:选择sym8小波并进行6层分解,采用改进的阈值去噪算法对带噪语音信号进行处理,并与传统的语音去噪算法进行比较[14]。

Fig.8 The pure speech signal waveform and the speech signal waveform with noise
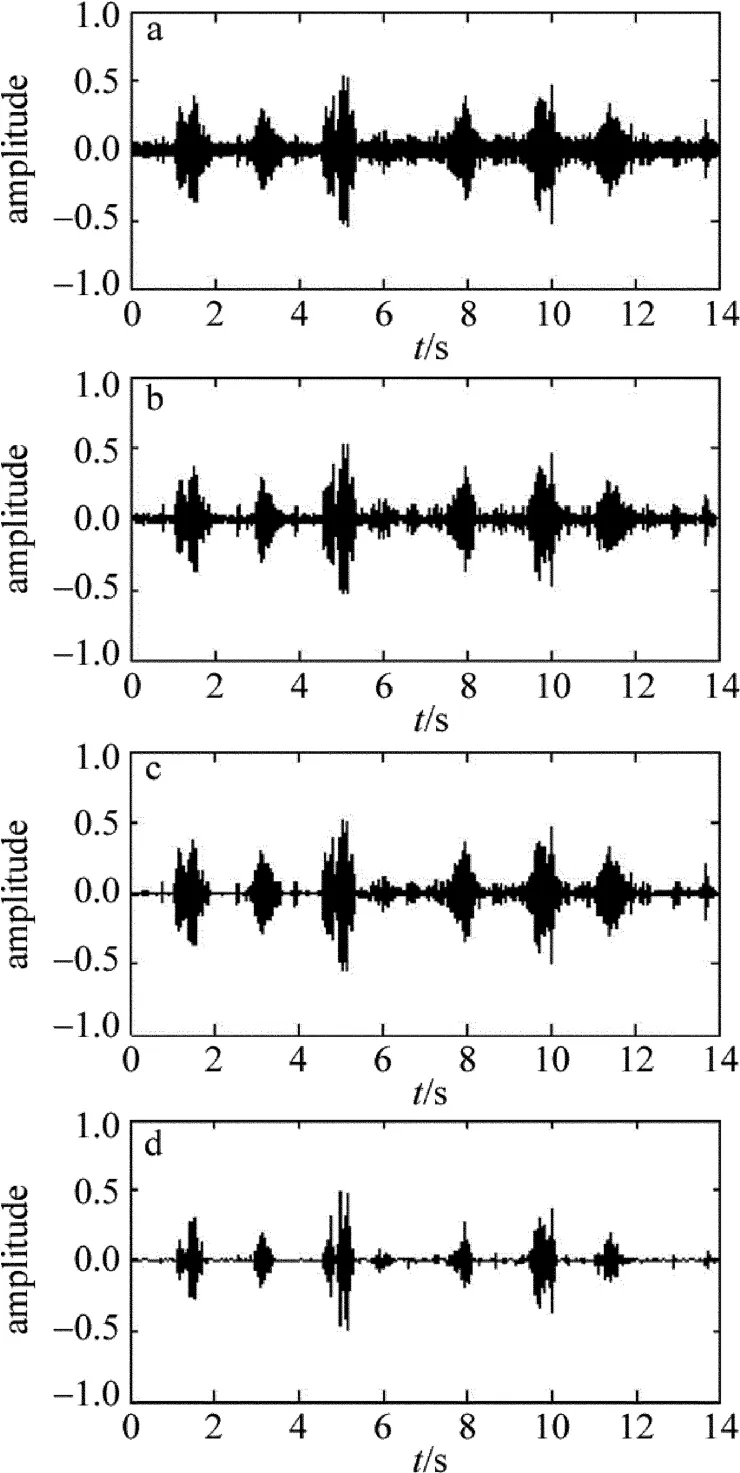
Fig.9 The denoised signal waveform using different methods
(1)对录制的音频信号“陕西省西安市”进行去噪处理。图8a是纯净语音信号,采样点数为112000,采样频率为8kHz;图8b是添加噪声后的语音信号,信噪比为15dB。不同方法去噪后的波形如图9所示。去噪后的信噪比如表2所示。
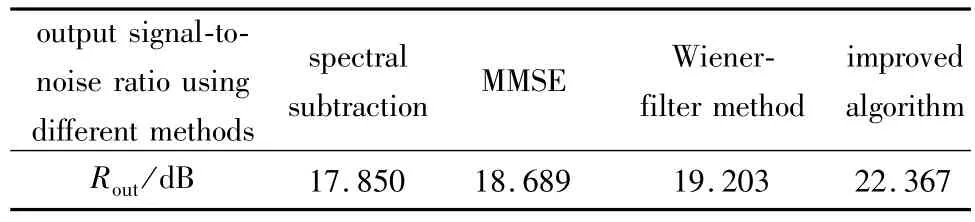
Table 2 Signal-to-noise ratio using different methods(Rin=15dB)
(2)对录制的音频信号“我是郴州的”进行去噪处理。图10a是纯净语音波形,采样点数为56000,采样频率为8kHz;图10b是添加噪声后的语音信号,信噪比为20dB。

Fig.10 The pure speech signal waveform and the speech signal waveform with noise
去噪后的信噪比如表3所示。
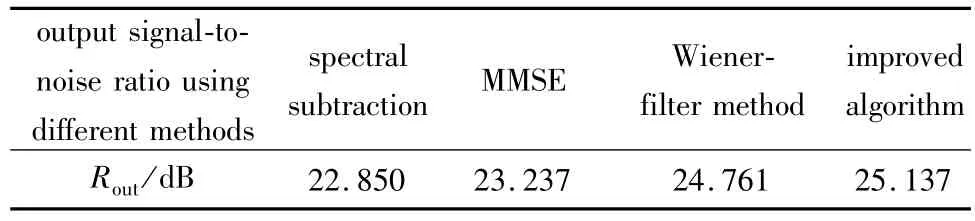
Table 3 Signal-to-noise ratio using different methods(Rin=20dB)
不同方法去噪后的波形如图11所示。
(3)下面对本文中改进算法和传统语音降噪算法的运算量进行比较。为了说明本文中改进算法的有效性,选取了一段12s长的带噪语音信号作为处理对象,各算法的处理时间如表4所示。

Table 4 Calculation cost of traditional algorithm compared with improved algorithm

Fig.11 The denoised signal waveform using different methods
从图8到图11可以看出:经过本文中的改进算法去噪后的语音波形和纯净语音信号的波形比较相近,与传统的去噪算法相比,本文中改进算法去噪后波形更平滑,几乎没有毛刺出现。从表2和表3可以看出:在信噪比指标方面,本文中的改进算法具有一定的优势,而且鲁棒性比较好。从表4可以看出,本文中改进算法在运算量方面也具有一定的优势。
6 结 论
综上所述,本文中改进算法不但兼顾了降噪效果和运算量两个指标,而且在去噪后的波形和信噪比都要好于传统的语音去噪算法,从而证明了本文中改进算法的有效性。
[1] GUO Ch Y,ZHENG K.Denoising optical interferometry signal based on wavelet transform threshold[J].Laser Technology,2009,37(5):506-508(in Chinese).
[2] WANG B,LIJW,WANG Zh F.Threshold de-noising method based on wavelet analysis[J].Computer Engineering and Design,2011,32(3):1099-1102(in Chinese).
[3] GUO Ch X.On the speaker recognition algorithm[J].Journal of Xi’an University of Post and Telecom,2010,15(5):104-106(in Chinese).
[4] ZHENGR,ZHANG Sh W,XU B.Improvement of speaker identification by combining prosodic features with acoustic features[C]//5th Chinese Conference on Biometric Recognition.Guangzhou:Lecture Notes in Computer Science,2004:569-576.
[5] YE H Sh,TAO JX,ZHANGDW.Improve speaker identification performance by integrating characters under noisy conditions[J].Computer Simulation,2009,26(3):325-328(in Chinese).
[6] GAN Zh G.An improved feature extraction method in speaker identification[C]//2011 Third International Conference on Intelligent Human-Machine Systems and Cybernetics.Hangzhou:IEEE,2011:218-222.
[7] McLAREN M,van LEEUWEN D.Source normalised and weighted LDA for robust speaker recognition using I-vectors[C]//IEEE International Conference on Acoustics,Speech and Signal Processing.Prague,Czech Republic:IEEE,2011:5456-5459.
[8] DU J,ZOU X,HAO J,et al.The efficiency of ICA-based representation analysis:application to speech feature extraction[J].Chinese Journal of Electronics,2011,20(2):287-292.
[9] ZHENG JW,WANGW L,ZHENG Z P.Speaker identification approach of hybrid GMM and RVM[J].Computer Simulation,2010,36(15):168-170(in Chinese).
[10] SAASTAMOINEN J,KARPOV E,HAUTAMAKIV,et al.Accuracy of MFCC-based speaker recognition in series 60 device[J].EURASIP Journalon Advances in Signal Processing,2005,37(17):2816-2827.
[11] WOOTERSC,HUIJBREGTSM.The ICSIRT07s speaker diarization system[J].Multimodal Technologies for Perception of Humans,2008,46(25):509-519.
[12] BOLL S.Suppression of acoustic noise in speech using spectral subtraction[J].IEEE Transactions on Acoustics,Speech and Signal Processing,1979,27(2):113-120.
[13] CHEN A M,VASEGHIS,MECOURT P.State based sub-band LP wiener filters for speech enhancement in car environments[J].IEEE Proceedings of International Conference on Acoustics,Speech and Signal Processing,2000,15(1):213-216.
[14] McAULAY R,MALPASS M.Speech enhancement using a softdecision noise suppression filter[J].IEEE Transaction on A-coustics,Speech and Signal Processing,1980,28(2):137-145.
An improved wavelet threshold algorithm applied in laser interception
QUZhi1,ZHANGBohu2
(1.Prostgraduare Brigade,Engineering College of China Armed Police Force,Xi’an 710086,China;2.Department of Communications Engineering,Engineering College of China Armed Police Force,Xi’an 710086,China)
In order to get better denoising result in laser interception,an improved wavelet threshold denoising algorithm was proposed.Through theoretical analysis and experimental verification,a series of simulation data were obtained.The results show that,compared with the traditional denoising algorithm,the speech signal-to-noise ratio after denoising is improved greatly.Denoising effect is obvious,signal waveform is smoother and distortion is less.
laser technique;denoising;wavelet threshold algorithm;simulation
TN249
A
10.7510/jgjs.issn.1001-3806.2014.02.016
1001-3806(2014)02-0218-07
屈 直(1989-),男,硕士研究生,现主要从事军事通信的研究。
*通讯联系人。E-mail:zbh62825@163.com
2013-06-04;
2013-07-06
