基于社交网络的单类协同过滤算法

李改，李磊

（1.顺德职业技术学院电子与信息工程学院，广东 顺德528333；2.中山大学信息科学与技术学院，广东 广州510006；3.中山大学软件研究所，广东 广州510275）

0 引言

随着互联网的快速发展，互联网上的数据量急剧增长，从而使得如何快速而高效地从如此浩瀚的数据海洋中获取我们所需要的信息变得越来越紧迫.在此背景下推荐系统应运而生，推荐系统通过收集和分析用户的各种信息来学习用户的兴趣和行为模式，根据分析得到用户的兴趣和行为模式，为用户推荐所需要的服务.这些系统的例子包括：卓越亚马逊（www.amazon.com）、当当网（www.dangdang.com）为用户推荐各种其可能喜欢的商品，如书籍、音像、电器、服装等；Netflix电影出租系统（www.netflix.com）为用户推荐各种其可能喜欢的电影.Google、Baidu、Yahoo等为用户推荐这种个性化的新闻和搜索服务.推荐系统中运用最广泛的是基于协同过滤的推荐算法［1－3］.

近年来协同过滤的算法在国内外得到了广泛研究，按处理数据的不同主要分为两类：一类是处理明确偏好的显式数据，如：评分.另一类则是处理无明确偏好的隐式数据，如：对网页点击与否.这种隐式数据广泛存在于真实世界的应用环境中，譬如用户是否购买过某个商品，用户是否点击过某个网页等等.由于这里信息不需要用户提供明确的评分，因此相比评分数据更容易获取.该类数据中仅有正例可以明确区分开来，负例不确定，故我们把该类问题称为单类协同过滤（OCCF）问题［4］.单类协同过滤的任务就是通过分析这些隐式信息来针对特定用户的偏好对推荐对象集按该用户的喜欢程度排序.尽管这类数据获取很容易，但该类数据极度稀疏且类高度不平衡，解释起来也存在很大困难.以用户点击网页的数据为例，这些数据中用户点击过的网页构成的数据可以解释为正例，其余绝大部分数据是负例和漏掉的正例的混合，如何解决数据的高度稀疏性及不平衡性问题，和如何解释这类混合数据并对解释后的数据进行有效处理，是当前单类协同过滤问题研究的难点所在.目前对该问题的研究还很少，C.Wang等把概率矩阵分解（PMF）技术运用到单类协同过滤问题［5］，他们把观察到的点击数据作为正例数据，其余的混合数据均作为负例数据，Zhang S等提出运用奇异值分解（SVD）技术来解决该类问题［6］.Rendle S等提出运用基于KNN的协同过滤算法来解决该类问题［7］.Pan等提出了运用加权的低秩逼近算法（OCCF）来解决该类问题［4］.

近来社交网络在协同过滤算法中的应用研究已经成为一个热点研究领域，如Ma等人就提出了在显式数据的推荐算法中引入社会化规范来提高推荐性能，同时解决带显式数据的推荐系统的数据稀疏性问题［8－12］.

在研究带显式数据的社会化推荐算法的基础上，提出一种新的基于社交网络的单类协同过滤推荐算法，即在Pan等提出的单类协同过滤算法的基础上引入社会化规范，以进一步提高单类协同过滤算法的性能，进而在真实的社会化数据集上实现本文中所提出的算法，并将其与几个传统的单类协同过滤算法的性能作比较.实验结果表明，SOCCF算法在各个性能评价指标下均优于几个传统的单类协同过滤算法.

1 基本定义和传统的单类协同过滤算法

1.1 基本定义 本文中矩阵用斜体大写字母表示（如：R），标量用小写字母表示（如：i，j）.给定一个矩阵R，Rij表示它的一个元素，Ri.表示矩阵R的第i行，R.j表示矩阵R 的第j列，RT表示矩阵R的转置.R－1表示矩阵R的逆.在本文中给定的矩阵R表示具有m个用户、n个对象的评分矩阵，矩阵U、V分别表示用户和推荐对象的特征矩阵.

1.2 传统的单类协同过滤算法 在传统的单类协同过滤算法［4］中为了找到一个低秩矩阵X来最大程度地逼近隐式数据矩阵R，我们最小化加权的Frobenius损失函数L（U，V）.

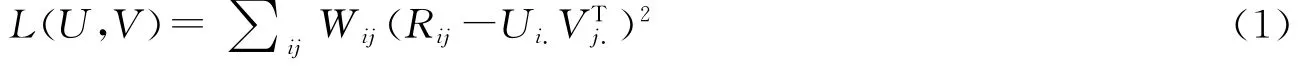
在目标函数L（U，V）中，（Rij－Ui.VTj.）是低秩逼近中常见平方误差项.Wij表示各个数据点对最小化总的加权的Frobenius损失函数的贡献，Wij＝θ∈［0，1］，具体的加权策略详见文献［4］.U、V 表示用户和推荐对象的特征矩阵.

为了防止过拟合，我们给（1）式加上正则化项，则（1）式可改写为：

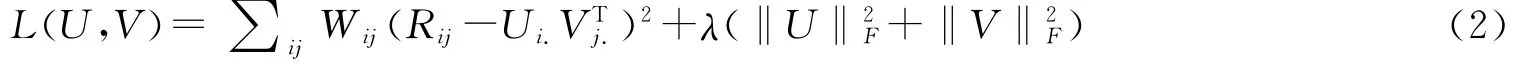
为了找到（2）式的最小值，可以通过对（2）式实施梯度下降法得到.固定V，对Ui.求导得到：

同理，固定U，对Vj.求导得到：

2 基于社交网络的单类协同过滤算法

2.1 基于社交网络的单类协同过滤算法 在传统的单类协同过滤算法（OCCF）的基础上引入社会化规范，进一步提高传统的单类协同过滤算法的性能.我们把本节中所提出的算法简称为SOCCF.

在这里我们假定，在社交网络中具有朋友关系的两个用户之间的特征向量相似，并且不同的评分相识性的用户之间的特征向量的相识程度也不同.在此引入下面的社会化正则项公式来对社交网络中具有朋友关系的两个用户之间的特征向量进行规范［8］.

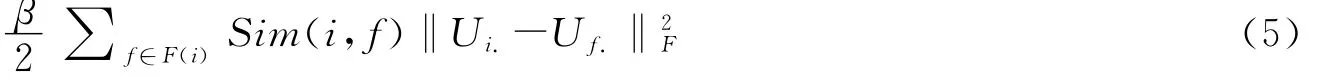
这里添加的社会化正则项是为了使得用户的特征向量尽可能与他的朋友的特征向量相似.参数β用于约束社交网络信息的影响.F（i）是用户ui的朋友集.‖Ui.－Uf.‖2F用于表示某个用户和他的朋友之间的偏好差异，用户ui和他的朋友uf之间的偏好差异越大，则‖Ui.－Uf.‖2F越大.其中Sim（i，f）表示用户ui和他的朋友uf之间的评分模式上的相似度.Sim（i，f）‖Ui.－Uf.‖2F表示用户ui和他的朋友uf通过相似度加权后的偏好差异.

在（5）式中Sim（i，f）用于计算用户ui和他的朋友uf之间的相似度，由于向量空间相似度（VSS）和皮尔生相关系数（PCC）均基于用户之间的共同评分项目集来计算相似度，而在现实世界中可能存在两个用户各自都有很多评分项，但这两个用户之间没有共同评分项目集，因此不能运用这两个函数来计算相应的用户间的相似度，从而导致这两个用户之间的社交网络信息丢失.为了解决该问题，提出的SOCCF算法采用了YU等提出的一种新的社会化相似度计算函数NSS使其能计算没有共同评分的用户间的相似度［11］：

这里Ui.和Uf.表示两个用户ui和uf的潜在特征向量.因此如果用户ui和uf偏好相同，则特征向量Ui.和Uf.也相近，从而算出来的两个用户ui和uf的相似度Sim（i，f）接近于1.如果运用向量空间相似度（VSS）和皮尔生相关系数（PCC）来计算相似度将导致没有共同评分项目集的用户之间的社会化信息丢失，因为YU等提出的NSS相似度计算方法，不需要的用户之间的共同评分项目集，因此不会导致用户之间的社会化信息丢失.

社会化正则项引入传统的单类协同过滤算法，我们就得到了本文中所提出的基于社交网络的单类协同过滤算法：

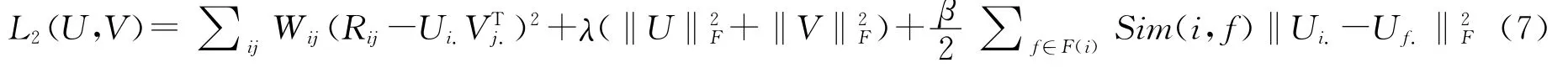
为了最小化损失函数，在（7）式上，对Ui.和Vj.实施梯度下降法，我们得到：

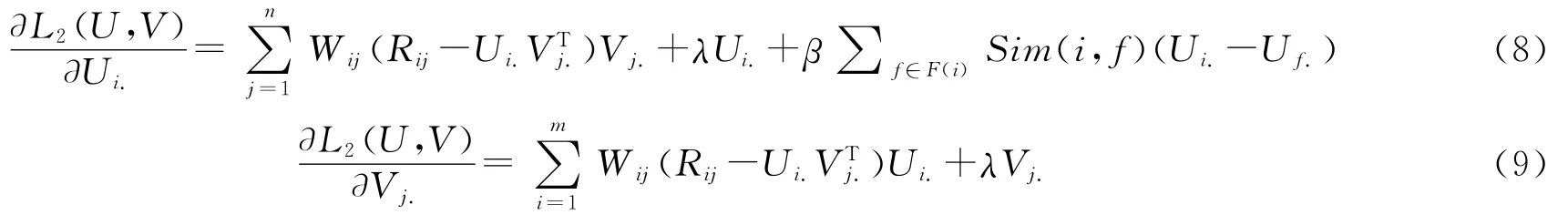
总结以上分析，我们给出SOCCF的求解算法如下：

算法1中的参数H表示一轮更新中所抽取的负例数据的个数与正例数据的个数相比的倍数.

2.2 算法计算复杂度分析 提出的SOCCF算法的计算复杂度主要与目标函数L2（U，V）和其各个偏导项的计算复杂度有关.分析（7）式，得到L（U，V）的计算复杂度为O（k＋2ρRmk），ρR表示评分矩阵R中正例评分点的个数，k表示特征矩阵U、V中的特征数表示用户的平均朋友个数，m 表示用户数.分析（8～9）式，得到偏导项的计算复杂度分别为O（ρRk2＋m）和O（ρRk2）.由于≪ρR，故一轮迭代中算法的复杂度为O（（H＋1）（ρRk2＋ρRk）），假定算法迭代d次后收敛，则整个算法的复杂度为O（d（H＋1）（ρRk2＋ρRk））.由于本算法采取抽样的随机梯度下降法来求解，迭代次数d将是一个常数.故本算法的时间复杂度与评分矩阵R中的正例数据点的个数线性相关.从以上分析可知，本文中所提的算法是一个高效算法，适合大数据的处理需要.

3 实验结果及分析

3.1 实验数据集 本实验中使用广泛运用的、公用的包含社交网络数据的数据集Epinions［11－12］.在这个数据集中，用户对其感兴趣的产品和服务进行评分，评分范围是1～5分的整数值.Epinions数据集中有用户的社交网络信息，这些关系与用户所信任的朋友的关系存在.Epinions数据集中包含49 290个用户，139 738个不同的评分项.总的评分数据点是664 824个.在社交网络中，总共有511 799个信任关系.为了把该数据集变为隐式数据集，所有有评分数据的数据点均设置评分值为1，其他没有评分数据的数据点设置评分值为0.经过上述处理，该Epinions数据集就变成了适合于单类协同过滤算法的数据集.

3.2 实验的评价标准 实验采用留一策略作为评价机制，也即我们从每个用户的评分历史中随机地选取并移除一个评分点作为测试集Stest，余下的数据构成训练集Strain，这两个集合不相交.我们在Strain上训练出相应的模型，接着在测试集上评估模型预测出的推荐对象的个性化排序.这里采用的评估标准是平均 AUC［7］：

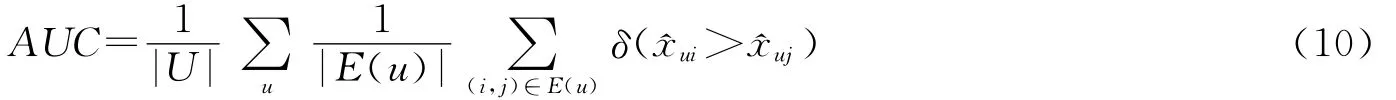
在这里δ是一个指标函数：

每个用户的评估对象为：

AUC值越高表示该算法的性能越好.由随机模型产生的AUC值为0.5，最好模型的AUC值为1.对每个实验我们均反复运行10次，每次均对每个用户随机选取一个评分点，构成新的训练集和测试集，最终结果取10次运算结果的平均值.

3.3 实验结果

3.3.1 规范化参数λ和β对SOCCF实验结果的影响 参数λ是正则化参数，可以通过交叉确认的方法学习得到，我们设置该参数为0.01.另一个参数β用于控制社交网络信息对SOCCF算法性能的影响.在极端情况下，如果我们设置参数β＝0，则在推荐过程中社交网络信息没有产生任何作用，推荐算法退化为传统的单类协同过滤推荐算法.

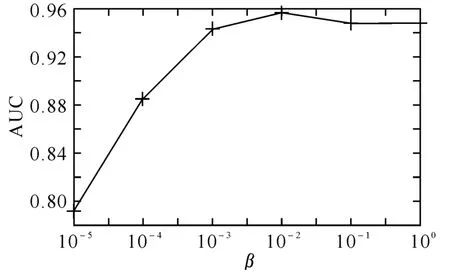
图1 参数β对算法SOCCF性能的影响

图1 显示了当特征数为5时，参数β对算法SOCCF的性能的影响，其中横轴表示参数β值的变化，纵轴表示算法SOCCF的AUC值.从图1不难看出开始随着参数β的增大，算法SOCCF的AUC值首先快速上升，随后又逐渐降低，参数β的最优值是0.01.这个结果正好和现实世界中朋友之间相互推荐的实际效果相符合，如果我们既考虑自身的喜好又考虑朋友的推荐，则我们就更能找到符合我们自己偏好的推荐对象.如果仅仅只是考虑自身喜好而忽略朋友的推荐，或者是仅仅考虑朋友的推荐而忽略自身的喜好，则都会走向极端，而不能得到最好的推荐效果.3.3.2 SOCCF算法和几个经典的单类协同过滤算法的性能比较 本文中所有算法均在装有Linux系统环境的计算机下运行，计算机配置环境是4核CPU，每个核主频是3.2GHz，内存是7.6G.各个算法的程序代码用Java开发工具Eclipse编写.各个算法均反复运行10次取平均结果作为该算法的最终运行结果.

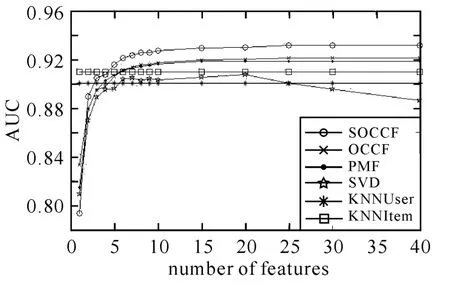
图2 SOCCF算法与其他经典单类协同过滤算法的比较

图2 表示在Epinions数据集上，所提出的SOCCF算法与传统的OCCF算法，PMF算法、SVD算法、基于用户的KNN算法（KNNUser）和基于项目的KNN算法（KNNItem）的性能对比.图1中横轴表示各个算法中用户／推荐对象的特征矩阵中特征的个数，特征个数从1变化到40，纵轴表示各个算法的AUC值.通过实验验证，SOCCF算法在Epinions数据集上取得最优值的负例权值参数θ为0.15，正则化参数λ为0.015 625.对于基于用户的KNN算法和基于项目的KNN算法，该实验中的结果取最优值，由于这两个算法的性能与特征矩阵中特征的个数无关，故在各个特征数下取值均一致.

从图2中可以看出在各个特征数下，提出的SOCCF算法几乎均优于传统的OCCF算法、PMF算法和SVD算法，也优于最优的基于用户的KNN算法（KNNUser）和基于项目的KNN算法（KNNItem），并且这种优势随着特征数的增加越发明显.其中SVD算法的AUC值随着特征数的增大先增大，而后急速下降，这是由于SVD算法在解决单类协同过滤问题时也出现了过拟合现象.

4 总结

在传统的单类协同过滤算法的基础上，引入社会化正则项，提出了一种新的基于社交网络的单类协同过滤算法.并以AUC值为性能评价标准，将其与传统的LRA算法、SVD算法、基于用户的KNN算法和基于项目的KNN算法的性能进行了比较，实验结果表明提出的SOCCF算法远优于其他几个经典的单类协同过滤推荐算法.在以后的工作中我们还将考虑SOCCF算法的冷启动问题、并行化的问题、以及与其他算法结合提出更加高性能的混合模型.

［1］Wu J L.Collaborative filtering on the Netflix prize dataset［D］.Beijing：Peking University，2010.

［2］Ricci F，Rokach L，Shapira B，et al.Recommender system handbook［M］.Belin：Springer，2011：12－120.

［3］Adomavicius G，Tuzhilin A.Toward the next generation of recommender systems：a survey of the state－of－the－art and possible extenstions［J］.TKDE，2005，17（6）：734－749.

［4］Pan R，Zhou Y，Cao B，et al.On e－class collaborative filtering［C］／／In IEEE International Conferenc e on Data Mining，2008：502－511.

［5］Wang C，Lei B，David M.Collaborative topic modeling for recommending scientic articles［C］／／Proceedings of the 2011Conference of the Knowledge Discovery and Data Mining，California，2011：448－456.

［6］Paterek A.Improving regularized singular value decomposition for collaborative filtering［C］／／in：KDD－Cup and Workshop，ACM press，2007：39－42.

［7］Rendle S，Freudenthaler C，Gantner，et al.BPR：bayesian personalized ranking from implicit feedback［C］／／In UAI，2009：452－461.

［8］Ma H，Zhou D Y，Liu C，et al.Recommendation systems with Social Regularization［C］／／In WSDM，2011：287－296.

［9］Zhu J K，Ma H，Chen C，et al.Social recommendation using low－rank semidefinite program［C］／／In AAAI，2011：158－163.

［10］Jamali M，Ester M.Matrix factorization technique with trust propagation for recommendation in social networks［C］／／In IJCAI，2011：2644－2649.

［11］Yu L，Pan R，Li Z.Adaptive social similarities for recommender systems［C］／／In Proceedings of the fifth ACM conference on Recommender systems（RecSys），2011：257－260.

［12］Tang J L，Hu X，Gao H J，et al.Exploitting local and global social context for recommendation［C］／／In IJCAI，2013：264－269.