自平衡两轮电动车控制系统设计与仿真

侯继红，马聪承，2

（1.广州科技贸易职业学院，广东 广州511442；2.华南理工大学机械与汽车工程学院，广东 广州510640）

0 引言

随汽车保有量不断增加带来的环境、能源和交通问题，很多汽车制造商和研究机构均研究设计混合动力、纯电动的四轮或两轮车.2001年，Segway Inc颠覆传统思想，生产出全世界第一台商业用途的双轮同轴平行布置载人自平衡电动车，这种车比传统双轮前后布置的电动单车在占地面积、转弯半径、运动灵活性等方面更有优势.近几年很多高校及科研机构开始对这种新型的交通工具进行研究［1］，所采用的控制算法有多种，如极点配置算法、模糊控制、自适应PID控制算法等，如Segway Inc的Segway PT（personal transporter）采用的冗余控制算法［2］、卡莫森学院研发的 HTV（human transporter vehicle）采用模糊控制［3］、阿德莱德大学研发的EDGAG采用PD控制［4］、中国科学技术大学研发的Free Mover采用PID控制等［5］.目前还缺少对各类方法在多种工况下（上下坡等）的仿真分析和比较.本文中借助MATALAB仿真软件进行自平衡两轮电动车的多工况下控制算法的设计及效果分析.

自平衡两轮电动车是车轮对称分布于车架的左右，中间为载人部分的车身，其结构跟一级倒立摆类似，属于自然不稳定系统［6－7］.要实现自平衡电动车直立行走，必须根据系统运动学及动力学方程并结合相关的控制算法设计自平衡控制器，以保持车的平衡.

自平衡两轮电动车的工作原理是：系统利用加速度、陀螺仪传感器，检测车身倾斜角度、倾角变化率、车速等姿态变化，用微处理器将感知车身姿态的传感器信号进行采样，经过计算得出车身倾斜角度、倾角变化率、车速等参数，并用这些参数转换成控制电机扭矩的PWM信号及驱动电机前进或后退动作，以保持车身的平衡.

本文中在对自平衡两轮电动车进行物理结构力学分析的基础上，用牛顿第二定律建立车的多输入、多输出非线性力学平衡方程，经计算化简及线性化处理得出系统状态方程.用此模型在MATLAB环境下利用acer极点配置、线性二次最优控制（RQL）算法设计控制器，仿真分析车在水平位置、15°斜坡时控制器对车身姿态及速度的控制情况，验证控制方法的可行性，比较两种控制算法对系统控制的性能.

1 自平衡两轮电动车系统建模

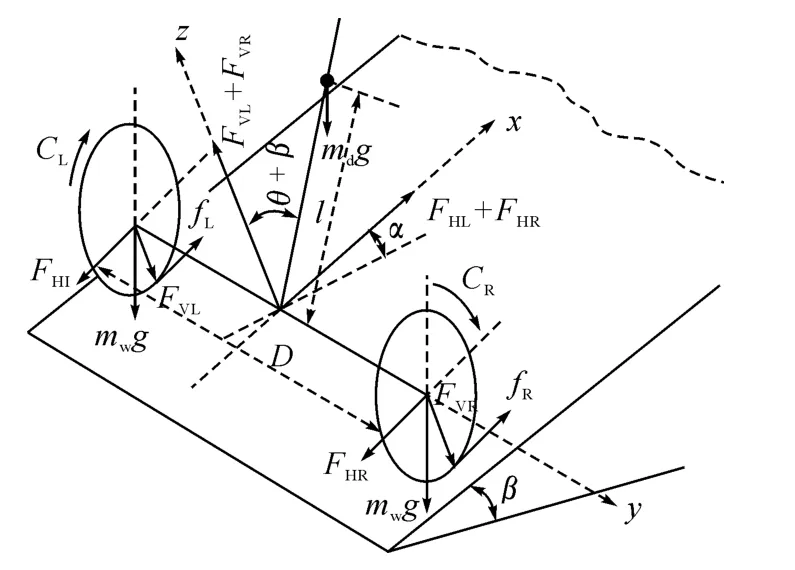
图1 自平衡两轮电动车在斜坡位置的受力分析图

1.1 系统受力分析 自平衡两轮电动车在斜坡位置的系统受力分析如图1所示［6］.车的行走方向为x轴，车轮轴线方向为y轴，与路面垂直方向为z轴，md为车体（包括驾驶员）的质量中心，θ为车体偏离平衡位置的倾角，α为车行驶的方位角，D为两轮之间的距离，l为质心到轮子轴心的距离，β为地面的斜坡度，fL、fR分别为左右轮与地面的摩擦力，CL、CR分别为左右电机的输出转矩，FHL、FHR分别为底盘与车轮在水平方向的作用力，mwg为车轮的重力，FVL、FVR分别为底盘与车轮在垂直方向的作用力，R为车轮的半径，以上参数的单位均为国际单位.

1.2 系统数学模型的建立 由上述力学模型，根据牛顿第二定律的力学分析方法建立力学平衡方程［8］.设左右车轮在x轴方向的位移分别为xL、xR，车体重心沿x轴方向的位移为xm，车体底盘沿x轴方向的位移为xd，车体重心绕y轴的转动惯量为Jθ，车轮绕轴心的转动惯量为Jw，车转弯时绕z轴的转动惯量为Jα.

根据牛顿第二定律，车轮的运动方程为：

同理，根据牛顿第二定律，车体的运动方程为：

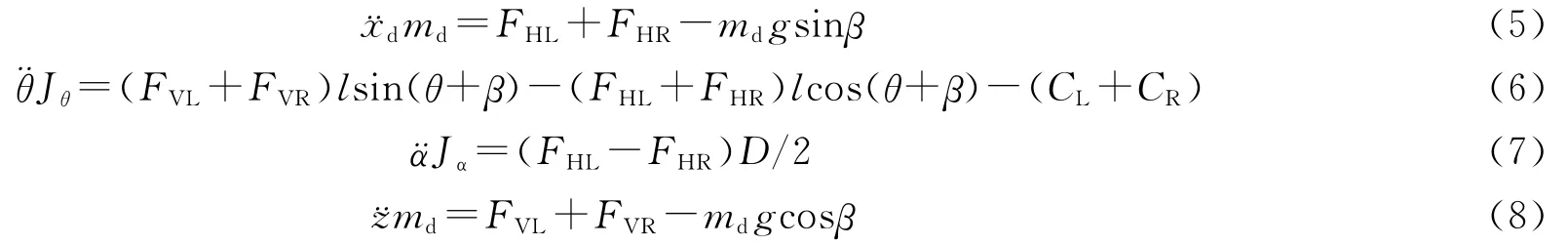
由车体的结构可知：

根据以上关系式，通过计算及化简，并在θ＝±5°处线性化处理，即取sinθ≈θ，cosθ≈1，˙θ2≈0，可将非线性的系统模型线性化为：

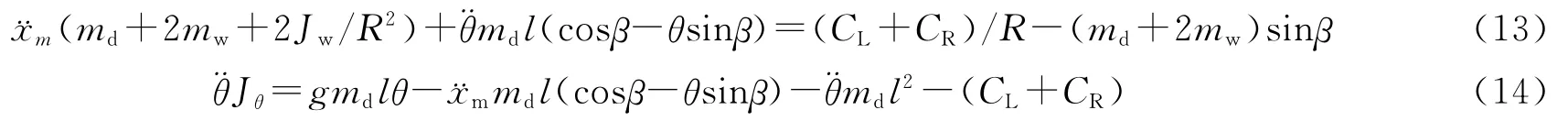
1.3 系统状态方程的建立 电动车的具体参数如下：md＝78kg，mw＝5.5kg，l＝0.85m，R＝0.12m，C＝18.569N·m，Jw＝0.039 6kg·m2，Jθ＝18.785kg·m2.

将电动车的参数及路面坡度代入（13）～（14）式，通过计算及化简，可得到水平路面（β＝0°）及坡度为15°的路面（β＝15°）的系统状态方程.

当车行驶在水平路面（β＝0°）时，系统的状态方程为：

当车行驶在坡度为15°的路面（β＝15°）时，系统的状态方程为：

式中A为系统矩阵，B为输入矩阵，C为输出矩阵，D为直接传递矩阵，X为状态向量，u为输入向量.

2 系统可控性分析

系统的可控性指输入对状态的控制能力，是极点可实现配置的充分条件；系统的可观性指表征输出对状态的反应能力.因此在设计系统控制器之前必须进行可控性、可观性分析［9］.

由可控性判断矩阵：

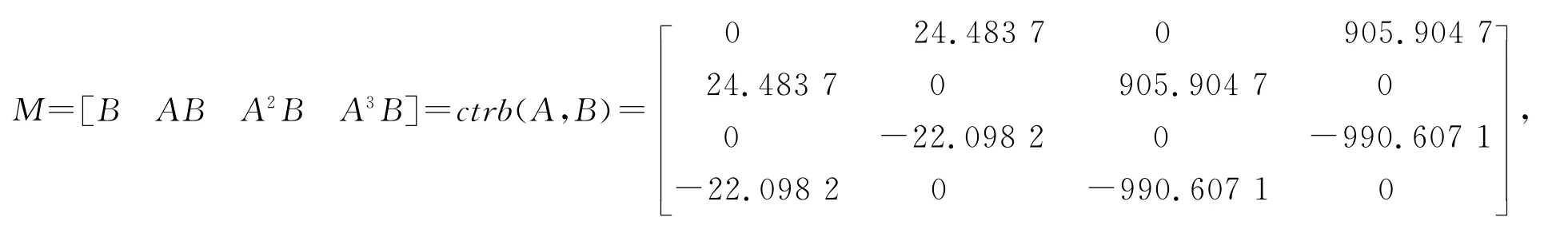
且rank（M）＝4，系统可控.

同理，由可观性判断矩阵：N＝［C CA CA2CA3］，可知rank（N）＝4，系统可观.

3 自平衡控制器设计

3.1 期望极点配置算法 系统状态方程是一个不稳定的开环系统，需要引入一个角度和位移组成的反馈量，将系统构成可控的闭环系统.根据系统控制理论，当线性系统加入反馈环节后，其状态反馈的控制规律为［9］

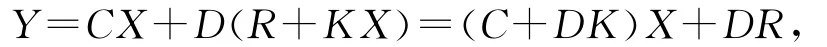
式中，A＋BK为闭环系统的系统矩阵，K为闭环系统的反馈增益，R为系统的参考输入，C＋DK为系统的输出矩阵.可以看出，闭环系统矩阵和输出矩阵均与反馈矩阵K有关，可以通过调整K以改善系统的稳定性、快速性、稳定误差及系统的可控性与可观性［10］.

通过设定期望极点方法求取反馈增益K，在MATLAB中通过acker函数根据期望极点求取K.在直角坐标平面的左半面，选取多组期望极点进行仿真，并对仿真结果进行比较分析，然后选取最优的期望极点，得到最优的反馈控制增益.下面以水平路面的系统状态为例，仿真分析期望极点选取对系统的影响.选取如下3组期望极点，以位移为研究对象，经过MATLAB仿真后，结果如图2所示.

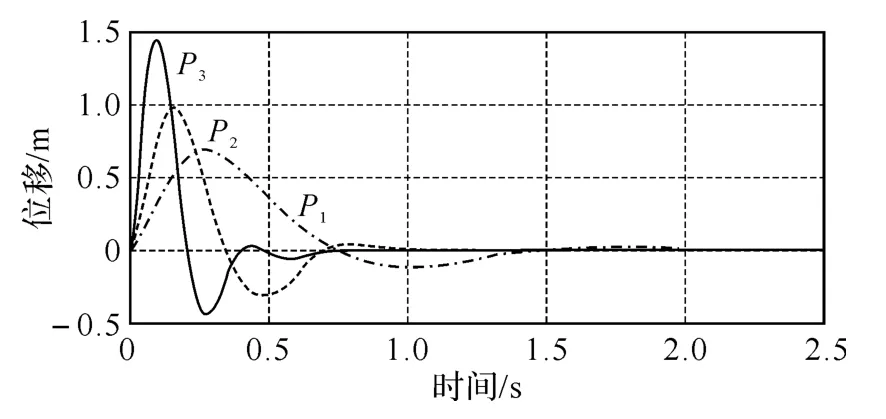
图2 不同期望极点下系统位移随时间变化的曲线

由图2可知，当配置极点远离坐标原点时，将加快曲线的收敛速度，提高系统的动态响应，减少系统到达稳定的时间，但增大了相对波动的幅度，同时增大了系统控制中所需的力，但当极点过远时，又会引起波动时间过长，导致系统控制过量，引起系统的不稳定.因此，需要选择合适的期望极点，使系统在获得较短的收敛时间的同时，不引起过大的超调量.通过上述分析，并要求车体在偏离平衡位置后，1s内回复到平衡位置，则选取系统状态反馈极点为： P＝［－3.5＋5j －3.5－5j －15 －30］.

分别将两个路面状态方程的常数矩阵A、B及选取的期望极点P，代入MATLAB的Acker（A，B，P）函数，分别得出与两个状态方程对应的反馈矩阵为：

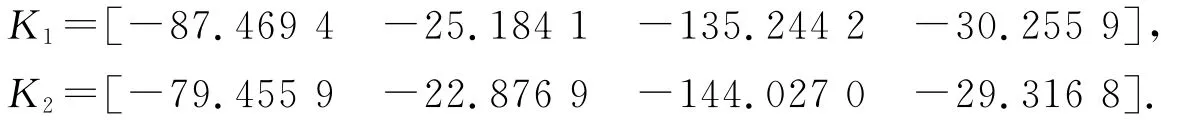
3.2 线性二次型最优控制算法（LQR） 除了用期望极点配置算法求取系统闭环控制的反馈增益外，还可用线性二次型最优控制算法（LQR）求取系统闭环的反馈增益.对可控、可观的系统，可通过MATLAB的LQR函数求取闭环系统最优的反馈增益，用最优的反馈增益构建闭环最优控制.通过Q和R的值平衡状态向量和输入向量，使性能指标J达到最优.

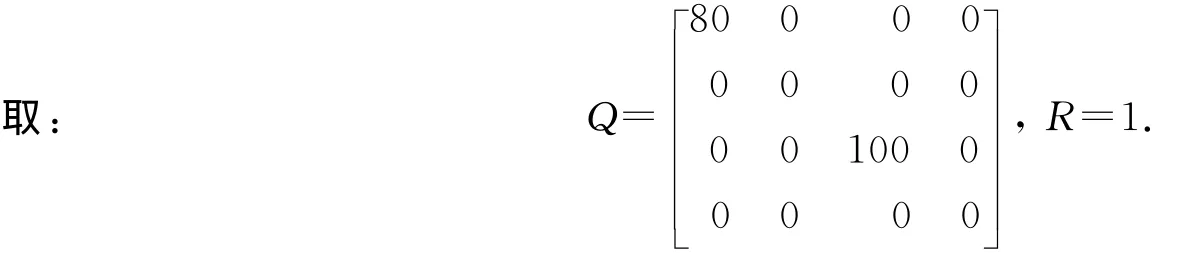
将车行驶在水平路面及坡度为15°路面的状态方程的A、B值及Q、R值代入MATLAB的函数（K，P，E）＝LQR（A，B，Q，R），分别求得两个路面坡度的最优反馈矩阵：

该反馈矩阵远小于用期望极点配置算法求得的反馈矩阵.

4 控制器仿真分析

为了验证期望极点配置及LQR两种算法设计的自平衡控制器的有效性，对系统进行了相应的仿真，并对仿真结果进行比较分析.

通过期望极点配置，为两种路面坡度系统状态找到了合适的反馈增益K1、K2.给系统设定0.087 27 rad（5°）的角度扰动为初始值，即x0＝［0 0 0.087 27 0］T，通过如下的 MATLAB 系统仿真程序：

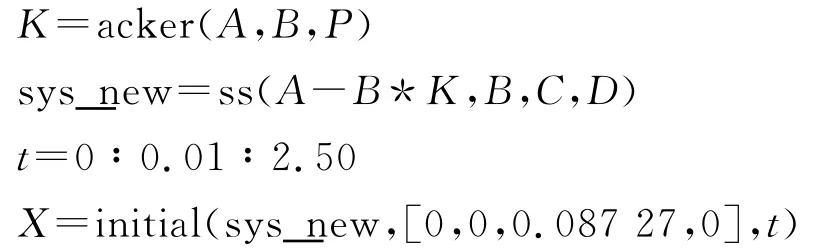
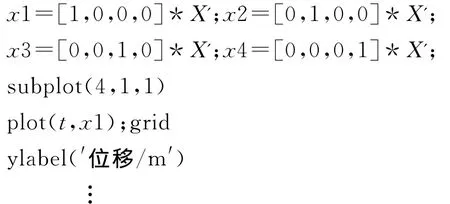
得出车的4个中间状态变量即位移、速度、车体倾斜角度及角速度响应曲线，如图3所示.由仿真曲线可知，无论车体在水平路面还是在斜坡路面，当车体受到0.087 27rad（5°）的扰动后，车的位移、速度、车体倾斜角度及角速度均在1s内回到平衡状态，扰动的角度越小，系统各变量回到平衡位置的时间越短.因此，可知系统模型线性化后的状态反馈设计达到系统控制的要求，并具有较好的控制效果.比较两图可知，斜坡路面系统调整的超调量比水平路面更小，且K值也小，说明上斜坡路面所需调整力也更小.

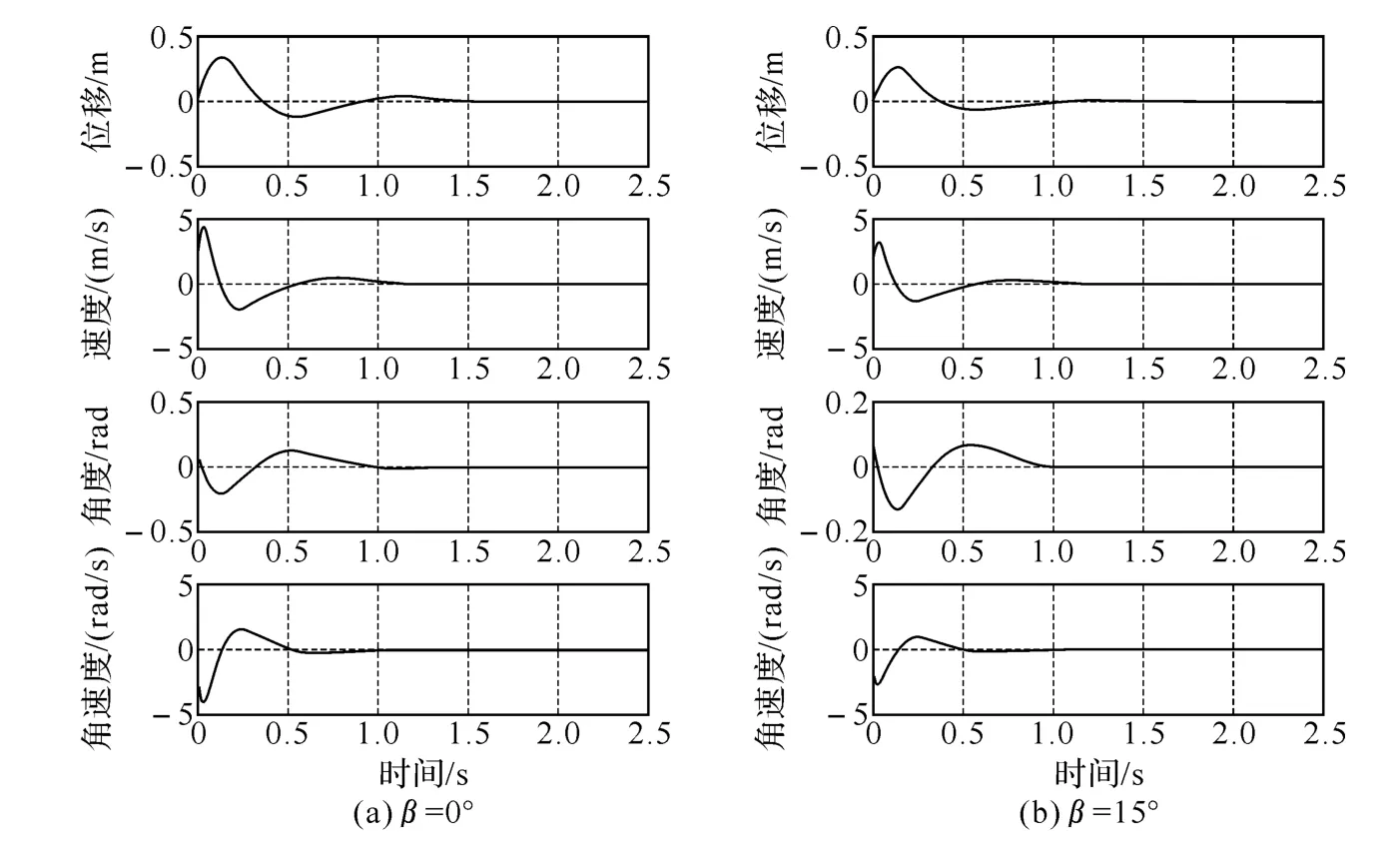
图3 期望极点配置算法系统仿真响应曲线图

LQR方法求取系统闭环的反馈增益K3、K4，代入MATLAB对给定系统初始条件x0＝［0 0 0.087 27 0］T系统仿真程序，系统仿真响应曲线如图4所示.由图可知，车体受到5°的扰动后，车体倾斜角度和角速度在0.5s内回到平衡位置，但不太稳定，位移回到平衡位置的时间较长，两种坡度路面的控制效果几乎一样.

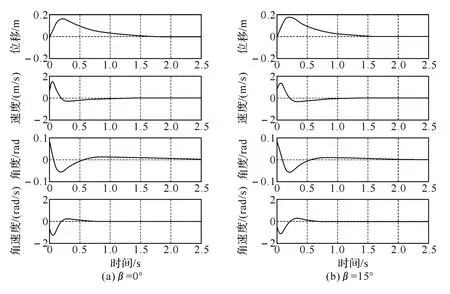
图4 线性二次型最优控制系统仿真响应曲线图

仿真结果表明，电动车在不同斜坡路面受到扰动时，LQR控制和极点配置控制均能较好地控制系统的稳定性，能够使车保持在平衡状态.对两种控制方法的仿真比较可知，LQR控制比期望极点配置控制的超调量小，但位移的收敛时间较长，且稳定性也较差，所以采用期望极点配置控制能使系统具有优良的稳定性，有更好的实际应用价值.

5 结束语

本文中对自平衡两轮电动车进行了系统动力学分析，利用牛顿第二定律建立系统动力学控制模型方程.分别采用期望极点配置算法和LQR算法设计控制器，并用MATLAB对两种方法设计的闭环控制器进行系统仿真.通过仿真验证所设计的两种闭环控制器能够使自平衡电动车的位移、速度、车体倾斜角度及角速度，在系统设计要求的收敛时间内逐渐趋于稳定.通过仿真分析，极点配置控制算法设计的控制器在系统稳定性方面优于LQR算法设计的控制器，具有更好实际应用价值.

［1］梁文宇，周惠兴，曹荣敏，等.双人载人自平衡控制系统研究系统综述［J］.控制工程，2010（5）：139－144.

［2］Grasser F，Darrigo A，Colombi S，et al.JOE：a mobile，inverted pendulum［J］.IEEE Transactions on Industrial Electronics，2002，49（1）：107－114.

［3］Beckwith B，Desjardins E，Howard C，et al.HTV project final report［R］.Victoria，Canada：Camosun College，2004.

［4］Baker N P，Brown C P，Dowling D R S，et al.SON of EDGAR，final report［R］.Adelaide Australia：The University of Adelaide，2006.

［5］屠运武.自平衡控制系统的研究［D］.长沙：中国科学技术大学，2004.

［6］阮晓刚，任红格.两轮自平衡机器人动力学建模机器平衡控制［J］.计算机应用研究，2009（1）：99－101.

［7］薛凡，孙京诰，严怀成.两轮平衡车的建模与控制研究［J］.化工自动化及仪表，2012（11）：1450－1454.

［8］杨兴明，余忠宇.自平衡控制系统的平衡性仿真［J］.计算机工程与应用，2011，47（24）：245－248.

［9］郑大钟.线性系统理论［M］.北京：清华大学出版社，2005：135－223.

［10］王正林.MATLAB／Simulink与控制系统仿真［M］.北京：电子工业出版社，2010：255－265.