基于自耦变压器的多电平注入式电流源型变换器
2014-06-22宋玉美游小杰孙倩倩郭希铮
宋玉美 游小杰 孙倩倩 郭希铮
(北京交通大学电气工程学院 北京 100044)
1 引言
大功率整流器广泛应用于电机调速、航空航天、高压直流输电及新能源系统,其强非线性和时变性,使其成为电网的主要谐波源[1,2]。而多脉波整流技术由于其结构简单、高效、高可靠性和低成本等优点,日益受到人们的关注和认可[3,4]。
最常见的多脉波整流技术为传统隔离型 12脉波整流器,但为了克服隔离变压器体积大的缺点,美国学者Derek A.Paice于1995年提出用自耦变压器代替隔离变压器的方法,通过合理的设计自耦变压器,其等效容量可达到 0.18Po,较隔离变压器1.03Po减小了82%,有效地降低了体积和成本[5]。
在一些谐波要求比较严格的大功率场合,12脉波整流电路的输入电流谐波不能满足要求,需要更多脉波数的整流电路。文献[6,7]给出了由更多整流桥构成18、24脉波数的整流电路,但该方法过于复杂且成本极高。多电平谐波注入融合了谐波注入、软开关等技术,成为实现多脉波整流技术的有效方法[8-10]。文献[11]将抽头变换器作为谐波注入电路与自耦变压器相结合,并给出24脉波整流电路拓扑的设计,但此方法需要选取最优电压比值,随着脉波数的增加计算比较复杂,并且主桥开关无法实现完全的零电流切换。文献[12]提出了一种新型注入电路,该注入方法便于拓展到多电平,同文献[6,7]中拓扑相比较,降低了对注入电路开关器件的电流容量和电流变化率的要求,并随着电平数的增多愈显优势,同时主桥开关能够实现零电流切换,并对网侧电压谐波有很好的抑制作用。
本文将自耦变压器与文献[12]提出的新型注入电路进行结合,得到新的基于自耦变压器的多电平注入式电流源型变换器拓扑结构,在减小变压器体积的前提下实现简易方便的多脉波整流,并对新拓扑的电压特性和电流特性分别进行分析,计算系统各部分容量大小,与传统自耦型12脉波整流拓扑进行对比,最后采用 Matlab对电路拓扑进行仿真验证,充分说明该拓扑在降低系统等效容量和减小输入电流谐波上的有效性。
2 系统结构及特性分析
本文所提出的基于自耦变压器的多电平注入式电流源型变流器拓扑,是在传统自耦型12脉波整流器的基础上,在直流侧加入多电平注入电路合成新的拓扑,如图1所示。整个系统由延边三角形结构自耦变压器、2组可控整流桥、零序电流抑制器(Zero-Sequence Blocking Transformer,ZSBT)和多电平注入电路组成,其中ZSBT的作用为抑制三倍频电流形成的零序电流,保证系统的正常运行。

图1 基于自耦变压器的多电平注入式电流源型变换器拓扑Fig.1 Topology of proposed multilevel injection current source converter employing the autotransformer
2.1 自耦变压器
系统中自耦变压器主要作用为提供移相电压,能实现此功能的自耦变压器有多种结构[13,14],常见的为延边三角形结构和zigzag结构。其中后者组成的多脉波整流器存在无零序电流环流、直流侧无需额外加入ZSBT且其与每个整流桥串联的电抗基本相等、电路对称性好等优点,但其显著的缺点是变压器电压比固定,应用于大功率场合将面临诸多问题。
延边三角形结构的自耦变压器一、二次侧变比k并不固定,可根据需要改变延边绕组抽头位置系数k1和延边比例系数k2来改变电压比值,如图2所示。上述三者之间的关系为
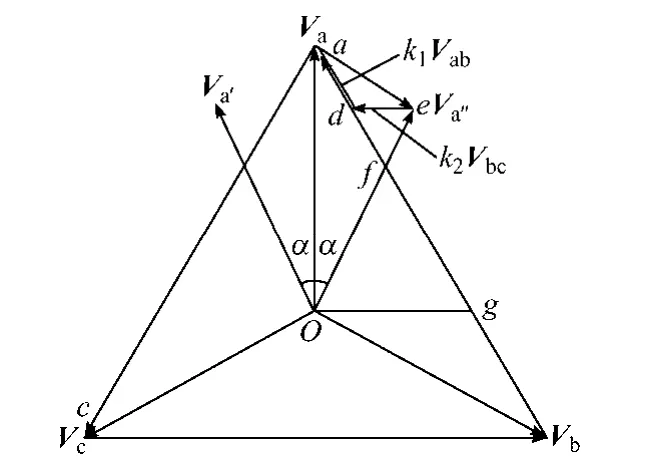
图2 延边三角形结构的自耦变压器矢量图Fig.2 The phasor diagrams of extended delta connection for autotransformer

经分析可知,延边位置系数k1和延边比例系数k2的变化,并不会引起系统输入电流的谐波畸变率。但为保证自耦变压器的体积和等效容量不能过大[15],需要在一定范围内选取延边位置系数,因此自耦变压器的电压比选取是有一定限制的,系统容量与延边位置系数k1的关系如图3所示。

图3 k1与k、系统容量之间的关系Fig.3 the relationship between k1and k,k1and the system capacity
本文采用自耦变压器选取k1=0的情况,其电压矢量图和磁路结构图如图4所示,为实现变压器二次侧两组电压相差30°,令a′V超前于aV15°,a′′V滞后于aV15°,因此有


图4 自耦变压器电压矢量图和磁路结构图Fig.4 The phasor diagram and magnetic circuit of autotransformer
根据矢量三角形合成原理可得变压器电压比为

2.2 直流侧输出电压分析
系统电压和电流特性随多电平注入电路的引入发生变化,因此需要做进一步分析。注入电路的拓扑图(以三电平为例)如图5a所示,两组整流桥经ZSBT后流向注入电路的电流分别是Id1和Id2,开关管VTj1~VTj4的触发脉冲如图5b所示,在满足VTj1和 VTj2互锁,VTj3和 VTj4互锁的前提下触发脉冲有多种组合方式,图5b中仅为其中的一种。
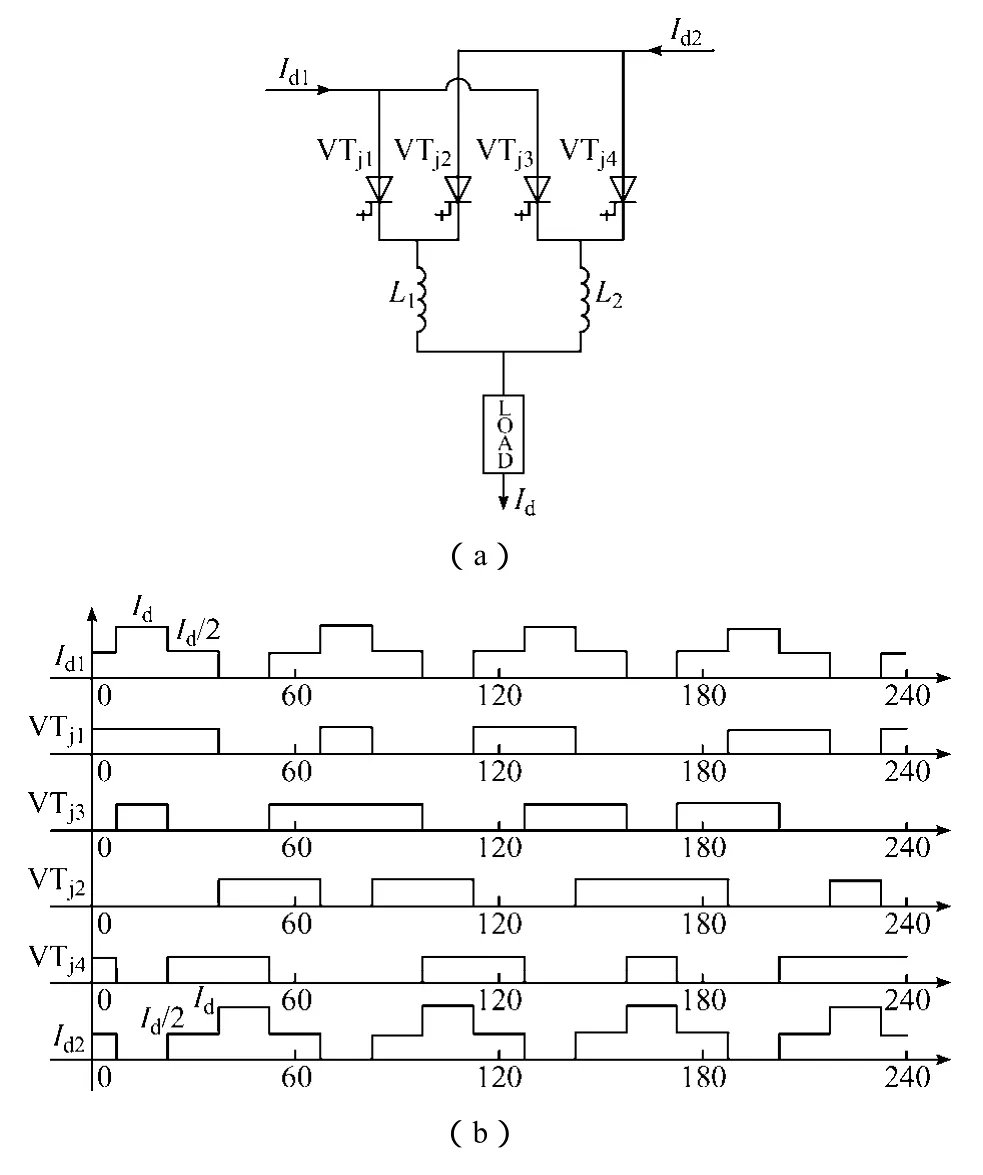
图5 注入电路拓扑图(三电平)及注入开关的触发脉冲Fig.5 The topology of reinjection circuit(three-level) and firing pulses of the reinjection switches
由于注入电路开关器件的切换,直流侧电压发生了改变,引入注入电路开关函数 pS、 qS,令
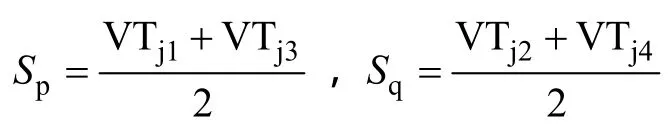
根据注入电路原理和电路拓扑图分析,可得直流侧输出电压为
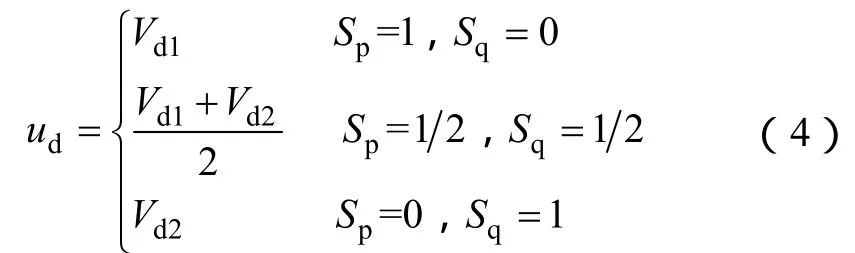
其中
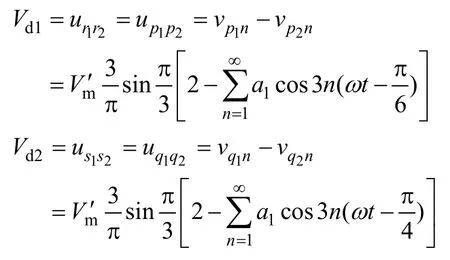
由式(4)计算可知,直流输出电压的平均值为

上式计算结果与未加注入电路时直流侧输出电压平均值相等,因此直流侧电压特性并未因注入电路的引入而发生改变。
2.3 交流侧电流分析
直流侧引入三电平注入电路后,整流桥输出电流Id1和Id2的波形如图5所示,令:

由式(6)可将系统直流侧电流分为两部分,分别为Id/2和im,因此交流侧电流ia也对应的由两部分组成,将其表示为

其中,ias与Id/2有关,为12脉波整流时交流侧电流;iam与im有关,为注入电流对系统输入电流的影响分量,上述三者的波形如图6所示。

图6 网侧电流ia及其两分量ias、iam波形图Fig.6 Current waveforms of ia,iasand iam
根据图4所示的自耦变压器磁路结构图和KCL定律可得

对ias进行傅里叶级数展开,其表达式为
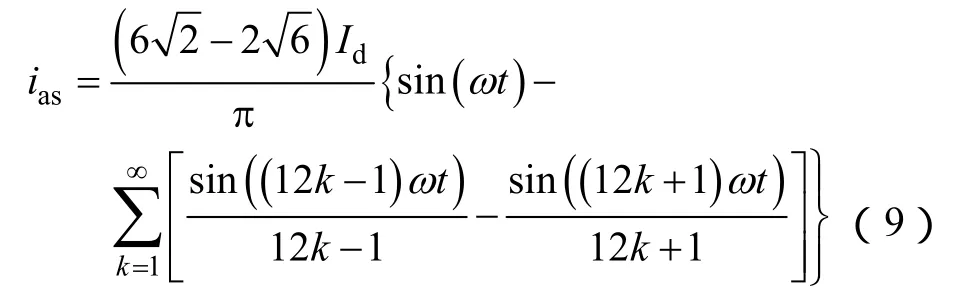

对iam进行傅里叶级数展开,其表达式为

由式(9)、式(10)可得

因此网侧电流的THD值为

式中,I1为网侧电流基波有效值;In为网侧电流 n次谐波有效值。
将ia和ias各次谐波含量进行对比,如表1所示,可以看出,与传统的12脉波整流器相对比,附加的注入电路所产生的附加电流,以 11次、13次谐波为主,并且与传统 12脉波整流器交流侧电流的11次、13次谐波相位相反,因此可大大减小 11次、13次谐波含量。

表1 不同拓扑的网侧电流谐波含量Tab.1 The current hamonics content of different topologies
3 系统容量计算
注入电路的加入,虽然对系统各部分的电压特性并没有造成影响,但系统电流发生了变化,因此系统各部分的容量也随之变化。在系统网侧电流谐波特性大大改善的前提下,需进一步对增加注入电路后的系统与传统自耦型 12脉波整流系统的容量进行比较,来确定本文提出新拓扑的应用价值。
以自耦变压器容量为例进行计算,自耦变压器由3个主绕组和6个抽头绕组组成,分别计算a相输入线电压 Vab、小绕组电压aaV′、a相主绕组电流I1以及小绕组上电流aI′的有效值,可得自耦变压器容量为

同理可得系统其他部分的容量值,并与传统自耦型12脉波整流系统相对比,如表2所示。

表2 传统拓扑与新拓扑系统的各部分容量Tab.2 The capacity of each part of the conventional topology and the proposed topology (单位%)
由上表可以看出,新拓扑在各部分容量较传统自耦型12脉波整流器均略有增加,但与隔离型 12脉波整流器容量相比仍大幅度减小,证明本文所提拓扑在系统容量上仍具有较大优势。
以上分析均以三电平注入电路为例,随着注入电平的增加,交流侧输入电流将更趋近于正弦波,其THD会随电平数增加而逐渐减小,系统容量也相应降低,如图7所示,由图可以看出,本文所提拓扑优势随电平数增长而大大提升。

图7 注入电平数与网测电流THD、系统容量的关系图Fig.7 the relationship between reinjection level number and THD of input current,capacity of the system
4 仿真验证
采用图1所示拓扑结构进行Matlab/Simulink仿真(三电平为例),系统参数为:变压器容量100kV·A,三相交流电源电压有效值220V,电网频率50Hz,注入电路支路电感50mH,负载电阻为1Ω。
图8给出了新拓扑的仿真结果,图中截取系统稳定后0.6~0.66s内一段波形,图8a为自耦变压器一次和二次a相电压波形图,从图中可看出,自耦变压器两组二次电压一组超前一次电压 15°,另一组滞后一次电压 15°,达到了移相 30°的目的;图8b、8c、8d分别为自耦变压器一次和两二次a相电流波形图,与理论推导相似;图8e为直流侧负载两端电压波形。

图8 系统仿真电压电流波形Fig.8 Simulated current and voltage waveforms of the system
图9所示为直流侧加注入电路前后,网侧电流THD对比图,由图可以看出,与传统自耦型12脉波整流器相对比,注入式多脉波整流器网侧电流的谐波含量可大大减小,两种拓扑各次谐波含量及THD值均与表1基本相符。

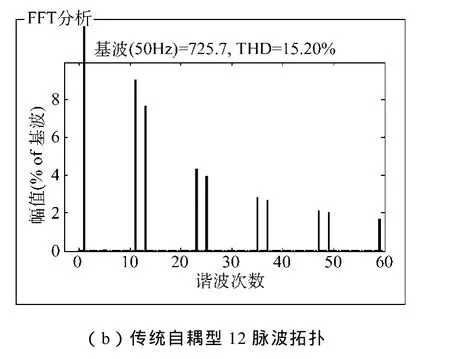
图9 两种拓扑网侧电流THD分析对比图Fig.9 The THD of the input current of two different topologies
5 结论
本文提出了一种新型的基于自耦变压器的多电平注入式电流源型变换器拓扑,该拓扑在融合了谐波注入、软开关等多种技术的基础上,克服了传统电流源型变换器交流侧需并联大容量电容器的缺点,使拓扑更加适用于诸多电流源特性的电力设备。同时,采用自耦变压器取代传统的隔离变压器达到电压移相的目的,大大减小了系统容量。
通过分析新拓扑的电压特性和电流特性,确定新拓扑在减小交流侧电流谐波和整个系统容量上的优势,为本文所提出系统的合理性提供了充分的理论依据和仿真验证。
[1] George J Wakileh.Power System Harmonics Fundamentals,Analysis and Filter Design[M].Berlin:Springer,2001.
[2] Jos Arrillaga,Neville R Watson,Power System Harmonics[M].England: John Wiley & Sons Ltd,2013.
[3] 朱屹,杨世彦,孟凡刚.直流侧带 PWM 整流器的12脉波整流系统及其负载适应性[J].电工技术学报,2012,27(8): 85-92.Zhu Yi,Yang Shiyan,Meng Fangang.12-pulse rectifier system with a PWM rectifier at DC side and its load adaptability[J].Transactions of China Electrotechnical Society,2012,27(8): 85-92.
[4] Derek A Paice.Power Electronic Converter Harmonics:Multipulse Methods for Clean Power[M].New York:IEEE Press,1995.
[5] Sewan Choi,Prasad N Enjeti,Ira J Pitel.Polyphase transformer arrangements with reduced kVA capacities for harmonic current reduction in rectifier-type utility interface[J].IEEE Transactions on Power Electronics,1996,11(5): 680-690.
[6] 马西庚,白丽娜.一种新型24脉波整流电路的设计及仿真[J].计算机仿真,2009,26(5): 262-265.Ma Xigeng,Bai Lina.Analysis and matlab simulation of a new 24-pulse rectification system[J].Computer Simulation,2009,26(5): 262-265.
[7] Sewan Choi,Bang Sup Lee,Prasad N.Enjeti.New 24-pulse diode rectifier system for utility interface of high-power AC motor drives[J].IEEE Transactions on Industry Applications,1997,33(2): 531-541.
[8] Lasantha B Perera,Yonghe Liu,Neville R Watson,et al.Multi-level current reinjection in double-bridge self-commutated current source conversion[J].Power Delivery,IEEE Transactions,2005,20(2): 984-991.
[9] Liu Yonghe.Multi-level voltage and current reinjection AC/DC conversion[D].New Zealand:Electrical and Computer Engineering at the University of Canterbury,2003.
[10] Arrillaga J,Yonghe H Liu,Neville R Watson.Self-Commutating Converters for High Power Applications[M].England: John Wiley & Sons Ltd,2009.
[11] 金孝忠.基于抽头变换方法的多脉波整流技术研究[D].哈尔滨工业大学,2009.
[12] 杨宝峰,吴振军,刘永和.一种新型并联三电平注入式电流型变换器拓扑[J].电工技术学报,2009,24(5): 67-72.Yang Baofeng,Wu Zhenjun,Liu Yonghe.A new topology of three-level reinjection current source converter in parallel[J].Transactions of China Electrotechnical Society,2009,24(5): 67-72.
[13] Bhim Singh,Sanjay Gairola.Zigzag connected autotransformer based controlled AC-DC converter for pulse multiplication[J].IEEE,2007: 889-894.
[14] 陈杰,龚春英,陈家伟.多脉波整流技术在风力发电中的应用[J].电工技术学报,2012,27(4): 131-144.Chen Jie,Gong Chunying,Chen Jiawei.Research on multi-pulse rectification technique in wind power application[J].Transactions of China Electrotechnical Society,2012,27(4): 131-144.
[15] Fanggang Meng,Wei Yang.Effect of voltage transformation ratio on the kilovoltampere for 12-pulse rectifier system[J].IEEE Transactions on Industrial Electronics,2013,60(9): 3579-3588.
