以静代动有限元原理及其在凸极类电机中的应用

王世山 虞振洋 谢仁和 龚 敏 秦海鸿

（南京航空航天大学江苏省新能源发电与电能变换重点实验室 南京 210016）

1 引言

制造及控制技术的提高使得电机向着特种化方向发展。开关磁阻、双凸极电机均不同于传统交、直流电机结构，属于凸极类电机，由于其固有的优点，非常适合需要高速、高温的航空领域使用[1,2]。然而，由于凸极电机工作原理不同于传统电机，采用传统经验或磁路方法的设计会对该类电机带来较大的误差[3,4]。因此，数值计算法，尤其是基于有限元算法的通用软件成为分析和设计该类电机的重要选择[5,6]。

理论上，可以令转子位于任意一位置角建立电机数值计算模型，但对于360º全区域则计算量急剧增大，即使仅考虑一对极之间的区域，对于极对数较少的高速电机计算量仍然很大，难以满足电机设计阶段以某一技术指标为目标的自动优化设计。如果以某一位置模型为基准，不同位置角对电机始终采用这一模型，仅修正不同的边界条件模拟电机转子的不同位置，则可大大减少数值计算规模，也可以简化程序，适合电机设计期间进行优化结构，本文将这一方法，称作“以静代动法”（Method of Motion Replaced by Rest,MRR）。

实质上，MRR即为如何处理电机定、转子相对运动的问题，处理这一问题有边界积分法[7]、耦合单元法[8]、预存储剖分法[9]、气隙单元法[10]和运动边界法[11]，其中边界法以能够保持有限元方程稀疏性、程序易实现性而更受欢迎，与本文所采用的MRR类似。文献[12]仅用少量内容阐述了运动边界法基本思路，也有文献采用类似方法对电机进行建模和仿真[13-15]，但目前尚未检索到文献将这一技术如何与损耗、优化结构结合在一起进行电机的设计。

毫无疑问，损耗是电机最重要特性之一，其值的大小决定了电机效率的高低，因此对损耗的预估对设计高品质的电机具有重要意义。

一般而言，电机的损耗包括线圈损耗、铁心损耗和杂散损耗[16]。线圈损耗，即使计及导线集肤效应，也有许多经典理论和算法提供其相关公式；杂散损耗，对于磁轴承、真空环境运行可忽略，对于低速普通环境电机可采用测量方式确定；唯有铁心损耗，由于结构和材料的复杂性，所以一直引起研究人员的关注[17-19]。

铁心损耗，根据引起损耗机理的不同，存在三种形式，即涡流、磁滞以及剩余。部分研究试图用实验方式对这三种损耗进行分离，然而即使采用实验法分离，则分离后的结果一般仅适合于特定设备，缺乏一种普遍性结果。文献[20]介绍，采用斯坦麦茨（Steinmaz）公式[21]，对中等强度磁场和较低频率下可忽略剩余损耗，对非正弦波形，引入波形系数进行校正，但是对非标准的非正弦波（如极不规则周期波），则这一公式也无能为力；文献[21]以54篇文献详细地综述了铁心内三种损耗的计算原则，其本质仍然是斯坦麦茨公式，差别仅在于磁滞损耗与磁通密度指数项的不同。

因此，本文结合凸极类电机特点，假定剩余损耗可忽略，对电枢电流频率产生的涡流损耗进行计算，有别于前述文献中涡流损耗系数必须经测量的环节。结合一次测量总损耗，确定磁滞损耗系数，由此可进一步预测铁心的各种损耗。

2 MRR有限元原理

2.1 电机静止状态磁场边值问题

对凸极类电机，以开关磁阻电机为例说明（双凸极电机类似）。设忽略电机端部效应，则一个截面可表示为如图1所示，其磁场分布可看作为一个2D平行平面场。对于求解该平行平面场，可选择矢量磁位A的z分量Az为自由度（简记为A），则

式中，Jc为激励电流区域的电流面密度；S1、S2分别为电机外边界和转轴内边界，可以选择为矢量磁位A的参考面。

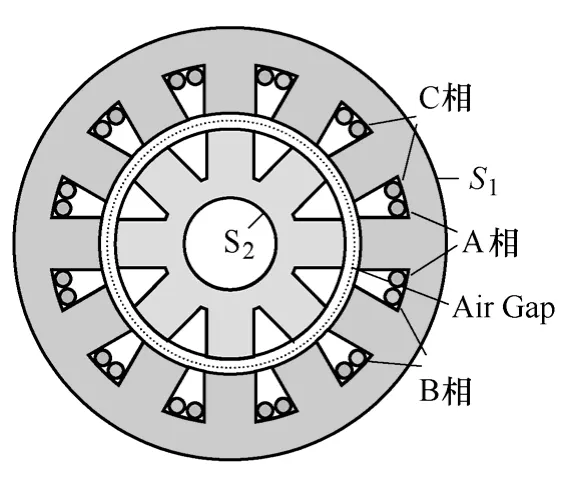
图1 凸极电机的一个平行平面截面Fig.1 A parallel plane cross-section of the salient motor

为体现电机的旋转效应，可将图1中的电机“定子”和“转子”分别建立模型，即“转子模型”建为图2a，该模型除包含实体转子外，外边界包含1/2厚度的空气间隙；“定子模型”为图2b，同样该模型除包含定子实体外，内边界也包含 1/2厚度空气间隙。

图2 子区域模型Fig.2 Sub-region model

假设转子边界 Gap1和定子边界 Gap2上分别均匀分布n个节点 p1,p2,…,pn和q1,q2,…,qn。设某一时刻 p1与q1重合，则p2和q2重合，…，pn和qn重合，则对应自由度一定相等，即

式（2）称作转子、定子区域边界的自由度耦合方程，与式（1）共同构成以分区域转子与定子建立时的边值问题。

若利用有限元对所建立的区域离散化，则该静态 2D平行平面磁场可求解，由此可进一步分析电机相关特性。

2.2 电机运动状态边值问题

因为电机电磁效应无“累计”效应，所以定、转子之间这种相对运动可以通过“时步”的方法处理。假设时刻t1时图2区域的位置，即（见图3a）

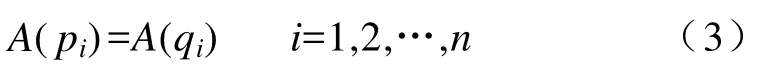
若时刻t2，即经过Δt=t2-t1，转子相对定子旋转了θ

则图3a的位置变为图3b，相当于转子逆时针方向旋转了θ角度，转子对应角速度

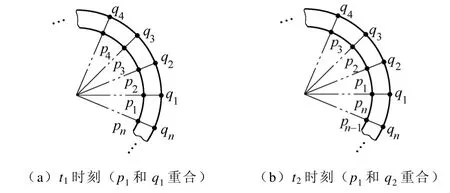
图3 定、转子边界运动状态Fig.3 Boundary movement with stator and rotor

此时自由度A在边界上的耦合方程为

由此转子实现了由p1至p2的旋转。若给定该旋转时间为Δt，则转子的转速由式（5）确定。

对编程而言，在实现式（6）之前，必须对式（2）的表达式进行“破坏”，即“解耦”才能实现式（6）。反复“耦合”+“解耦”+“错位耦合”，则360º形成一个全区域旋转状态，由此可进行旋转状态下电机磁场的求解，本文将这一方法称作“以静代动”（Motion Replaced by Rest，MRR）法。

当通过有限元求解整个区域各节点磁位A后，则任意节点和单元内的磁感应强度B也可求解，对于专业化有限元软件均可自动获得，为分析和解决相关问题带来极大的方便。

若式（5）中的ω 为常数，则根据不同的θ对应不同的时刻 t，则可获得某一固定转速下各物理量随时间的变化规律，如图4所示。

图4 电机物理量随时间变化Fig.4 Physical quantity of motor via time

2.3 分区域的边界—气隙的剖分

图5 气隙层剖分Fig.5 Meshing for air gap layer

根据耦合边界节点必须为均匀分布，而转子和定子有凸极的特点，则图5转子侧空气A和定子侧空气B必须为自由（Free）剖分，而邻近边界区C和D可选择用均匀“映射”（Mapped）剖分。

3 电机稳定旋转状态下损耗求解

电机的稳定运行状态下其损耗包括电枢损耗和铁心损耗。在电枢损耗电流谐波成分较小及漏磁较小的条件下，电枢损耗可以按直流损耗计算，也可以参考变压器中导体涡流损耗的方法进行计算[22,23]；铁心损耗则包含涡流损耗、磁滞损耗和剩余损耗[24]。虽然电机结构不同，但由于引起其损耗的机理相同，所以不同电机类型间这些损耗的计算方法可以相互借鉴。

3.1 涡流损耗

3.1.1 涡流损耗构成及矩形薄片涡流损耗

贯穿电机铁心内的磁感应强度在圆柱坐标系下可分解为 Br、Bθ和 Bz三个方向的分量（图6见），它们分别在截面 S1/S3（上下面）、S5/S6（左右面）和S2/S3（前后面）上产生涡流及其损耗。对于可忽略电机端部效应的磁场，则Bz=0，S2/S3截面上的涡流可以忽略。因此，涡流损耗仅由Br、Bθ所决定。

事实上，从涡流损耗的角度来看，Br、Bθ所产生的效应相同，因此只需通过研究一种正弦激励磁场在一类硅钢片中的损耗，并在此基础上对所有铁心涡流损耗叠加即可。

假设图6硅钢片为矩形（见图7），有激励磁场

图6 电机铁心涡流损耗构成Fig.6 Consisting of eddy current power loss inside core

图7 处于磁场中的矩形硅钢片Fig.7 Silicon steel sheet immersed in the magnetic field

对忽略每片铁心边缘效应时，其涡流损耗为[25]

与综量Kt有关的函数f(Kt) 反映了硅钢片在外加激励下的去磁效应

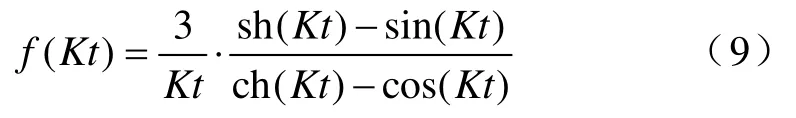
当 Kt数值很小时，则 f(Kt)≈1，如 Kt＜2.4，f(Kt) 仅引起5%的误差，则单位体积的涡流损耗为

当数值较大时（经计算 Kt＞4.0），则 f(Kt)≈3/(Kt)，则

3.1.2 电机硅钢片涡流损耗

对于可简化为2D磁场硅钢片涡流计算，式（8）S为硅钢片的截面面积。因此，涡流计算时矩形截面的面积S成为影响其值的重要因素。

在有限元数值计算中，硅钢片截面可剖分为三角形和四边形，而式（8）理论上仅适合于矩形截面。然而，任意三角形、非矩形四边形剖分单元总可以通过足够多的矩形逼近及合成，只要这些矩形截面内的材料特性相同、磁感应强度也相同，则该单元的涡流损耗完全可以根据式（8）计算，只是S变为剖分单元的面积即可。

由图4可见，铁心内的B一定为周期非正弦激励。若对铁心内的B进行傅里叶分解，即分解为具有n次谐波的合成

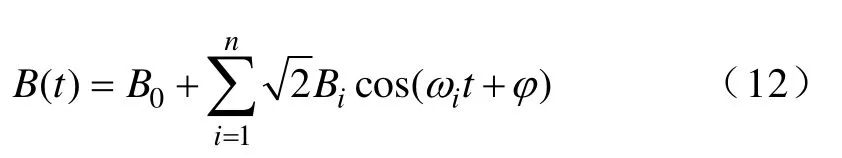
其中，直流分量B0不产生涡流以及损耗，对每一次谐波i代入式（8）进行涡流计算，则一个剖分单元在图4随时间变化的磁场激励下，其涡流损耗为

对一剖分为Ne的硅钢片，则其涡流损耗为

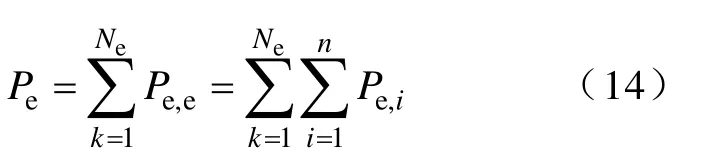
3.2 磁滞损耗系数

磁滞损耗，由磁畴的不可逆移动而引起的损耗，由于其精确计算涉及材料的微观结构，所以电气工程界经常结合一定的经验获取该损耗值。

据Steinmaz公式，对电力设备中的铁心损耗，剩余损耗可以忽略不计，则铁心损耗为

式中，Pe,s为式（14）考虑所有硅钢片后的涡流损耗，而磁滞损耗Ph为

式中，Kh为与频率f无关，仅与硅钢片厚度、材质有关的常数；指数α可以通过严格的实验测定，但是对于大多数不具备实验条件的研究，可以近似选取，本文根据相关实验发现取 1.6可取得较好结果。

假设对某一规格铁心电机，设法测定式（15）中的 Psteel，若能够较准确地计算到其中的 Pe,s，则式（15）中的Kh为

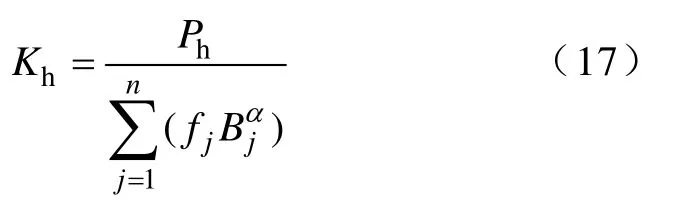
由此，可通过测量电机的总铁心损耗，结合涡流计算公式可以间接近似计算出某一规格硅钢片的磁滞损耗系数Kh。假设以该类硅钢片制造任何型式的电机，则可以将式（17）中的 Kh代入式（16），即可计算不同电机采用同类硅钢片的磁滞损耗。

4 双凸极电机损耗的求解及其验证

4.1 样机结构

选用一台额定功率为 45kW，定转子极数为30/20的三相电励磁双凸极发电机进行损耗的求解和验证，其中硅钢片采用 DW310-35，叠压系数为0.95，额定转速为2 200r/min，电机结构示意图如图8所示，结构参数见表1。

图8 电机结构Fig.8 The structure of motor

表1 样机结构Tab.1 The dimension of the motor prototype

4.2 MRR实施

对电机进行2-D有限元建立模型，剖分如图9所示。考虑到计算精度，铁心和气隙全部采用具有中间节点的四边形单元，即八节点四边形单元。

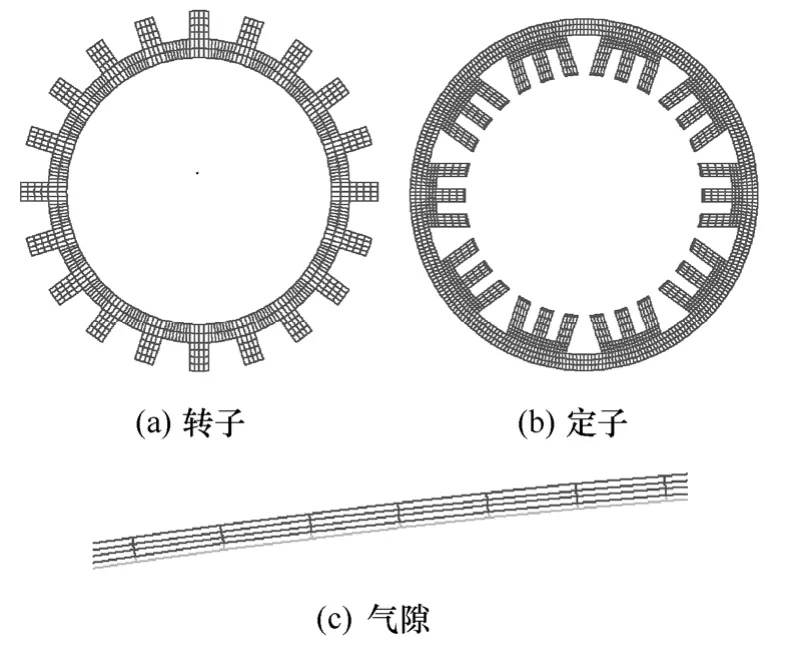
图9 模型剖分Fig.9 Meshing of the model

对表1结构模型，剖分单元数为6 380，节点数为19 100。模型剖分后，对30/20的双凸极实施MRR的，图10示意了不同机械角度时磁通密度分布状况。

图10 MRR下的磁通密度分布Fig.10 Flux density distribution using MRR method

图10显示，定转子的相对位置没有改变，但磁通密度分布变化。0º时磁通密度在转子A处和定子B处是连续的，通过MRR法转动9º后，磁通密度出现不连续。事实上，定子D位置磁通密度是与转子C处的磁通密度连续，这是因为转子已经发生了转动。

4.3 样机电枢绕组的电感特性

为了得到加载的电枢电流波形，必须要得到电机运行时各相的自感以及相绕组和励磁绕组之间的互感。

若仅对某一相绕组通电流 Ii，提取整个求解区域的能量Wm，则i绕组的自感为

若仅对两相绕组i、j分别通电流Ii、Ij，则整个求解区域的能量为

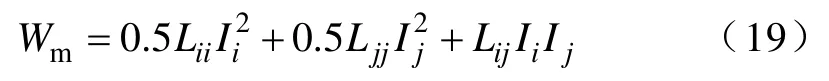
在采用式（18）的方法分别求得两绕组自感Li和Lj的基础上，则互感Lij立即可以求得；由此，对A、B、C三相绕组以及励磁绕组而言，可以求得其电感的空间分布（见图11、图12）。

图11 三相绕组电感Fig.11 Three-phase winding inductance

图12 相绕组和励磁绕组互感Fig.12 Mutual inductance between phase winding and excitation one

双凸极电机相自感和相-励磁互感具有同样的变化趋势，但是由于三相间的互感数值及其变化很小的缘故，所以三相绕组的互感可忽略不计。

4.4 功率变换电路及电枢电流

本文的双凸极电机系统中，功率变换器采用三相桥式电路（见图13）。

图13 开关主电路Fig.13 Main switch circuit

对该电路拓扑建立Simulink模型，将有限元软件ANSYS的计算电感数据导入（见图11、图12），采用标准角控制法进行仿真，得到三相电枢绕组的驱动电流（见图14）。

图14 三相驱动电流（If=6.41A）Fig.14 Three-phase driving current(If=6.41A)

4.5 磁滞损耗系数计算

用 MRR法对电机模型进行转动分析，提取空载工作下加载不同励磁电流时的转子铁心齿部的磁通密度值B，并进行傅里叶分解（见图15、图16）。图例为 1 100r/min下空载运行，选取 72º机械角为一个周期，转子每 1.5º转动一次，则采样工作点N=(72/1.5)+1=49。傅里叶分解的谐波次数 k=[(49-3)/2+1]次=23次，基频f0=5n/60=91.67Hz。

图15、图16显示，铁心中的磁通密度只有奇数次谐波，这是由于转子齿中切向和环向磁通密度在一个周期内半波对称。

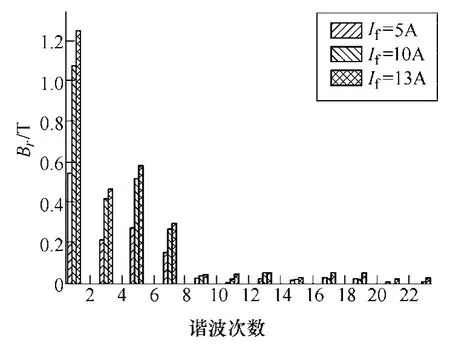
图15 径向磁通密度傅里叶分解Fig.15 Fourier decomposition on flux density along radial direction

图16 环向磁通密度傅里叶分解Fig.16 Fourier decomposition on flux density along toroidal direction

通过电机不同励磁电流和转速下空载实验测得的总损耗与风摩损耗的差值表示铁心损耗（见表2），涡流损耗用式（8）、式（9）和式（14）来计算得出，根据式（15），得出总的磁滞损耗，再根据式（17）计算出磁滞损耗系数（见表3）。

表2 不同工况下空载损耗Tab.2 No-load losses at different working conditions

表3 不同工况下的磁滞损耗系数Tab.3 Hysteresis loss coefficient at the different working conditions

表3显示，磁滞损耗系数在不同工况下变化很小，也验证了磁滞损耗系数的特性。对于同一规格的硅钢片可以取平均值进行计算，该电机的硅钢片的磁滞损耗系数取Kh=0.77。

4.6 电机损耗

将磁滞损耗系数 Kh代入式（16），就可计算该电机的磁滞损耗了，进而可以计算求解出电机的铁心损耗。

本文以样机在发电下运行的实验测得的steelP′数据和ANSYS有限元软件计算出的铁心损耗Psteel进行比较，分析误差H（表4）。

表4 1 100r/min下各个工况下的损耗Tab.4 Losses at the speed of 1 100r/min under different working conditions

由表4中的H得知，满足误差在15%以内，具有参考意义。因此可以将该系数用于其他采用DW310-35硅钢片的双凸极电机中进行设计仿真。

5 结论

本文以旋转状态下的电机为研究对象，采用以某一位置的 2D有限元法建立了对应磁场模型，提出了求解电机损耗的方法，并以双凸极电机为例取得了与实验一致的结果，得到如下结论：

（1）以静代动的有限元法理论上可以求解任何旋转类设备的磁场分布问题。选择矢量磁位A为自由度，对定、转子及相邻部分的气隙层分别建立有限元模型，令其接触的空气边界自由度不断“耦合”及“解耦+滑动+再耦合”，可以模拟电机的旋转状态，由此可以求解旋转状态的磁场分布。

（2）采用以静代动的有限元法求解定、转子中每一单元内磁通密度随时间的变化，由此可获得每一铁心单元磁通密度的所有谐波构成，进一步可求解得到每一单元的涡流、磁滞和剩余损耗。

（3）以双凸极电机为例，若选择某一规格电机为样机，结合测试电机总损耗则可间接获取一种规格硅钢片磁滞损耗系数，由此可进一步计算采用同类硅钢片电机的各类损耗，为设计电机期间损耗的计算奠定了一定的理论基础。

[1] Desai P C,Krishnamurthy M,Schofield N,et al Novel switched reluctance machine configuration with higher number of rotor poles than stator poles concept to implementation[C].IEEE Trans.on Industrial Electronics,2010: 649-659.

[2] 戴卫力,马长山,朱德明.双凸极电机的结构设计与系统控制[M].北京: 机械工业出版社,2011

[3] 程明,周鹗,黄秀留.双凸极变速永磁电机的变结构等效磁路模型[J].中国电机工程学报,2001,21(5): 23-28.Cheng Ming,Zhou E,Huang Xiuliu.Variable structure equivalent magnetic circuit modeling for doubly salient permanent magnet machine[J].Proceedings of the CSEE,2001,21(5): 23-28.

[4] 魏静微,谭勇,张宏宇.大型交流励磁双馈风力发电机的设计[J].电机与控制学报,2010,14(5): 44-48.Wei Jingwei,Tan Yong,Zhang Hongyu.Design of AC-excited doubly-fed wind power generator with large capacity[J].Electric Machines and Control,2010,14(5): 44-48.

[5] 凌岳伦,王勉华,王岩,等.基于 Ansoft开关磁阻电机建模与控制策略的仿真研究[J].电机技术,2009(2): 20-23.Ling Yuelun,Wang Mianhua,Wang Yan,et al.Simulation study on modeling and control strategy of the switched reluctance motor based on Ansoft[J].Electrical Machinery Technology,2009(2): 20-23.

[6] 陈志辉,周楠.混合励磁双凸极电机三维有限元仿真与数字电压调节技术[J].中国电机工程学报,2010,30(27): 26-31.Chen Zhihui,Zhou Nan.3-D finite element simulation and digital voltage regulation of a doubly salient hybrid excitation generator[J].Proceedings of the CSEE ,2010,30(27): 26-31.

[7] Sadowski N,Lefevre Y,Lajoie Mazenc M,et al.Finite element torque calculation in electricalmachines while considering the movement[J].IEEE Trans.on Mag.,1990,28(2): 1410-1413.

[8] Davat B,Ren Z,Lajoie Mazenc M.The movement in field modeling[J].IEEE Trans.on Mag.,1985,21(6):2298-2299.

[9] Tang Renyuan,Li Ge,et al.The application of finite element method to the design of REPM synchronous generators[J].IEEE Trans.on Mag.,1985,21(6):2472-2475.

[10] Abdel Razek A A,Coulomb J L,Feliachi M,et al.The calculation of electromagnetic torque in saturated electric machines within combined numerical and analytical solutions of the field equations[J].IEEE Trans.on Mag.,1981,6(11): 3250- 3252.

[11] 孙玉田,杨明,李北芳．电机动态有限元法中的运动问题[J].大电机技术,1997(6): 35-39.Sun Yutian,Yang Ming,Li Beifang.The moving problem in the dynamic fem of electric machines[J].Large Electric Machine and Hydraulic Turbine,1997(6): 35-39.

[12] 严登俊,刘瑞芳,胡敏强,等.处理电磁场有限元运动问题的新方法[J].中国电机工程学报,2003,23(8): 164-167.Yan Dengjun,Liu Ruifang,Hu Minqiang,et al.A new method to deal with the motion problem in electromagnetic field finite element analysis[J].Proceedings of the CSEE,2003,23(8): 164-167.

[13] 王爱龙,熊光煜.无刷双馈电机时步有限元分析[J].中国电机工程学报,2008,28(21): 123-127.Wang Ailong,Xiong Guangyu.Analysis of brushless doubly-fed machine by time stepping finite element method[J].Proceedings of the CSEE,2008,28(21):123-127.

[14] 刘瑞芳,严登俊,胡敏强.永磁无刷直流电动机场路耦合运动时步有限元分析[J].中国电机工程学报,2007,27(12): 59-64.Liu Ruifang,Yan Dengjun,Hu Minqiang.Field circuit and movement coupled time stepping finite element analysis on permanent magnet brushless DC motors[J].Proceedings of the CSEE,2007,27(12):59-64.

[15] Yuqi Rang,Hao Xiong,Qiang Wu,et al.FEM simulation and harmonic torque analysis of six-phase BLDC motor[C].2nd International Conference on Artificial Intelligence,Management Science and Electronic Commerce,Zhengzhou,China,August 8-10,2011: 3984-3987.

[16] 陈世坤.电机设计[M].北京: 机械工业出版社,2000.

[17] 孔晓光,王凤翔,徐云龙,等.高速永磁电机铁耗的分析和计算[J].电机与控制学报,2010,14(9):26-30.Kong Xiaoguang,Wang Fengxiang,Xu Yunlong,et al.Analysis and calculation of iron losses of high-speed permanent magnet machines[J].Electric Machines and Control,2010,14(9): 26-30.

[18] Huang Y,Zhu J,Guo Y.Thermal analysis of high-speed SMC motor based on thermal network and 3-D FEA with rotational core loss included[J].IEEE Trans.on Mag.,2009,45(10): 4680-4683.

[19] Seo J,Chung T,Lee C,et al.Harmonic iron loss analysis of electrical machines for high-speed operation considering driving condition[J].IEEE Trans.on Mag.,2009,45(10): 4656-4659.

[20] 颜威利,杨庆新,汪友华,等.电气工程电磁场数值分析[M].北京: 机械工业出版社,2005.

[21] 沈建新,李鹏,郝鹤,等.高速永磁无刷电机电磁损耗的研究概况[J].中国电机工程学报,2013,33(3): 62-74.Shen Jianxin,Li Peng,Hao He,et al.Study on electromagnetic losses in high-speed permanent magnet brushless machines-the state of the art[J].Proceedings of the CSEE,2013,33(3): 62-74.

[22] 王世山,汲胜昌,李彦明.变压器束绞圆导线线圈中涡流损耗的研究[J].高电压技术,2003,29(5):7-10.Wang Shishan,Ji Shengchang,Li Yangming.Numerical analysis of eddy current losses for power transformer windings with round stranded conductors[J].High Voltage Engineering,2003,29(5): 7-10.

[23] 毛行奎,陈为.反激式变换器的变压器线圈涡流损耗机制分析与新型损耗模型[J].电工技术学报,2009,29(3): 29-35.Mao Xingkui,Chen Wei.Mechanism investigation and analytical modeling for winding loss of flyback transformer[J].Proceedings of the CSEE,2009,29(3):29-35.

[24] Wang Fengxiang,Xu Yunlong,Zhang Dianhai.Study on core loss of high speed PM machine[C].IEEE International Conference on Industrial Technology.Gippsland,USA,2009: 1-4.

[25] Boglietti A,Lazzari M,Pastorelli M.A simplified method for the iron losses prediction in soft magnetic materials with arbitrary voltage supply[C].IEEE-IAS Annual Meeting,Piscataway,USA,2000: 269-276.