对“一种广义水驱特征曲线”的质疑、对比与评论

陈元千，郭二鹏，赵卫蕊，张霞林

（1.中国石油勘探开发研究院，北京100083；2.北京奥伯特石油科技有限公司，北京100084）

俞启泰教授在《石油勘探与开发》第25 卷第5 期发表了“一种广义水驱特征曲线”［1］一文，1998年发布实施的国家行业标准《石油可采储量计算方法》［2］，引入该曲线并将其定名为“俞启泰水驱曲线”，其影响不可小觑。然而，该曲线的建立过程简单且不严格，所提供的预测方法存在不确定性和不可靠性。为尽可能减少其在应用过程中可能产生的问题，在此对其提出质疑、对比与评论，以期与大家共同交流、探讨。

1 对俞氏广义水驱曲线的质疑

1.1 水驱曲线建立的不确定性

为正面理解俞氏广义水驱曲线的性质，应先了解它的建立过程。在文献［1］中，通过引用文献［3］中未经理论推导，且缺乏实际应用依据的表达式：

式中：Np为累计产油量，104t；Wp为累计产水量，104t；Lp为累计产液量，104t；a′为系数。

以及文献［4］中存在相同问题的表达式：

俞氏直接写出所谓的通式：

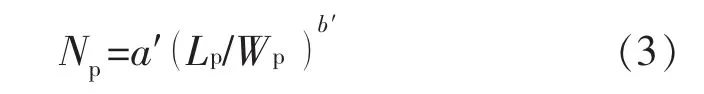
式中：b′为指数系数。

可以看出，俞氏广义水驱曲线的基础关系式，是经过一个简单而可疑的过程建立起来的。应当指出，式（1）和式（2）是2 个具有不同自变量的公式，不可能具有相同的系数a′，也不可能由此建立通式。

文献［1］通过对式（3）两边取常用对数，并令a=lg a′，b=-b′，得到俞氏广义水驱曲线的表达式：

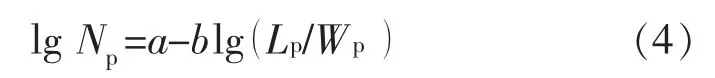
由式（4）可以看出，它是一个双对数直线关系式，不能因其在不同油田应用时具有不同的b 值，而将其称为广义水驱曲线。

1.2 累计产油量与含水率关系式的不可靠性

在文献［1］中，未经任何推导，直接由式（4）给出了累计产油量Np与含水率fw的关系式：

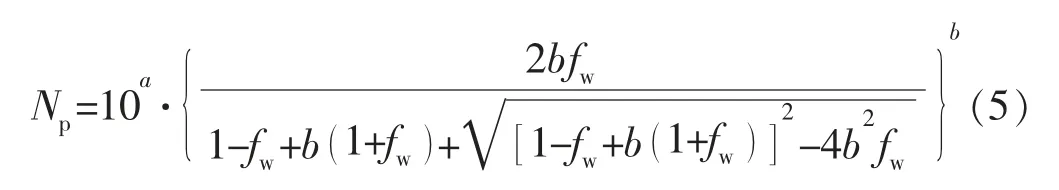
应当指出，式（4）是一个比较简单的关系式，将其两边对时间t 求导，结合dNp/dt=Qo，dWp/dt=Qw和Qw/Qo=fw/ 1-fw（）等关系式，却无法得到式（5）。因此，不能不对式（5）的正确性和可靠性再次提出质疑。

1.3 最大可采储量表达式的不合理性

预测水驱开发油田可采储量，是水驱曲线的重要功能之一。然而，在文献［1］中，未经任何推导和原理阐述，就直接提出了确定所谓最大可采储量NRmax的表达式：

究竟什么是最大可采储量？它是如何定义的？有何实用价值？ 在此，有必要对它的来源加以探讨。

假定Lp=Wp，则Lp/Wp=1，此时由式（4）可得到

应当指出，式（7）中的Np与式（6）中的NRmax显然不是同一个概念。由于Lp=Np+Wp，此时Lp=Wp的假设与之相悖，可见式（6）显然是不合理的。

其实，若取fw=0.98（极限含水率），由式（5）即可得到俞氏方法可采储量NR的计算式为

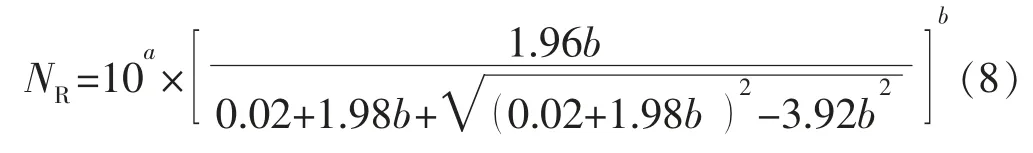
然而令人不解的是，俞氏在文献［1］中为何缺少用于确定可采储量的式（8）呢？当然，由于式（4）本身存在不可靠性，那么由其推导得出的式（8）也必然会令人心生质疑。尽管当定义fw=1 时，对应的累计产油量就是最大可采储量，此时可由式（5）简化整理得到式（6），但是由此假设得出的最大可采储量有何实际意义呢？

2 水驱曲线的应用与对比

为进一步分析俞氏广义水驱曲线的特性与适用性，利用一个实例，对俞氏广义水驱曲线、甲型水驱曲线和丙型水驱曲线进行应用对比［6-8］。

2.1 甲型和丙型水驱曲线

甲型水驱曲线关系式为［5］

式中：a1，b1分别为甲型水驱曲线的直线截距和斜率。

由式（9）可推导得出Np与fw之间的关系式为

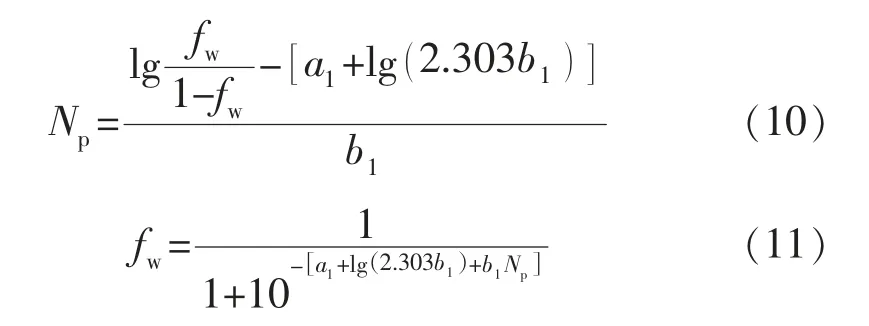
取fw=0.98 时，由式（10）得到可采储量为

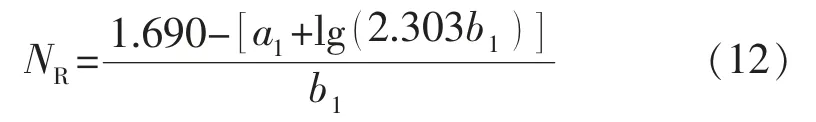
丙型水驱曲线关系式为［5］

式中：a2，b2分别为丙型水驱曲线的直线截距和斜率。

由式（13）可推导得出Np与fw之间的关系式为

当fw取为0.98 时，由式（14）得到可采储量为

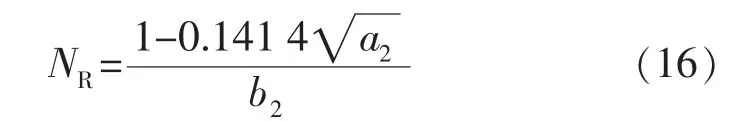
2.2 实例应用对比

利用大庆油田萨北过渡带开发区实际生产数据［9］，绘制了“广义”、甲型和丙型水驱曲线（见图1—3）。对各水驱曲线进行线性回归，并将线性回归后求得的截距、斜率值分别代入式（5）、式（11）和式（15），进行含水率与累计产油量关系式预测（见图4）。可以看出，俞氏广义水驱曲线的预测结果与实际数据吻合情况整体较差，开发中后期的含水率预测值偏低。

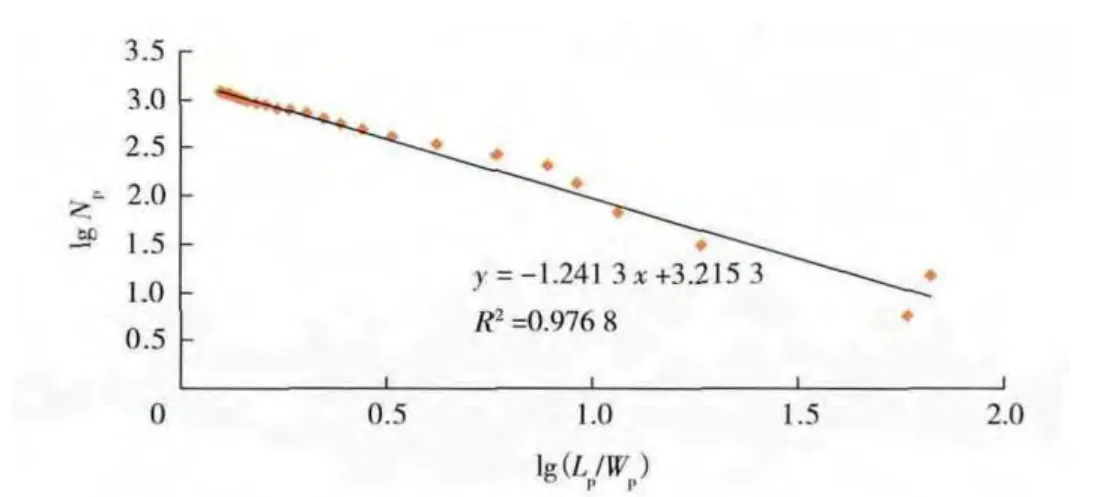
图1 俞氏广义水驱曲线

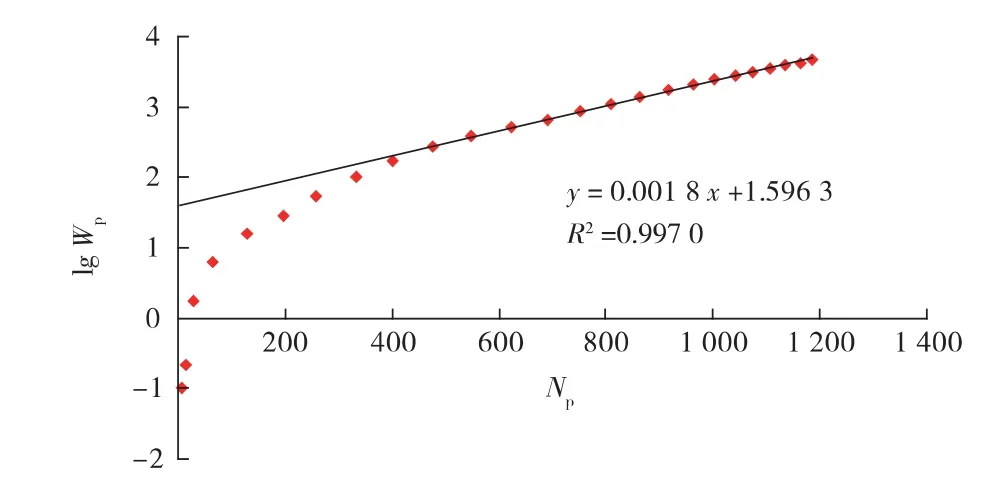
图2 甲型水驱曲线

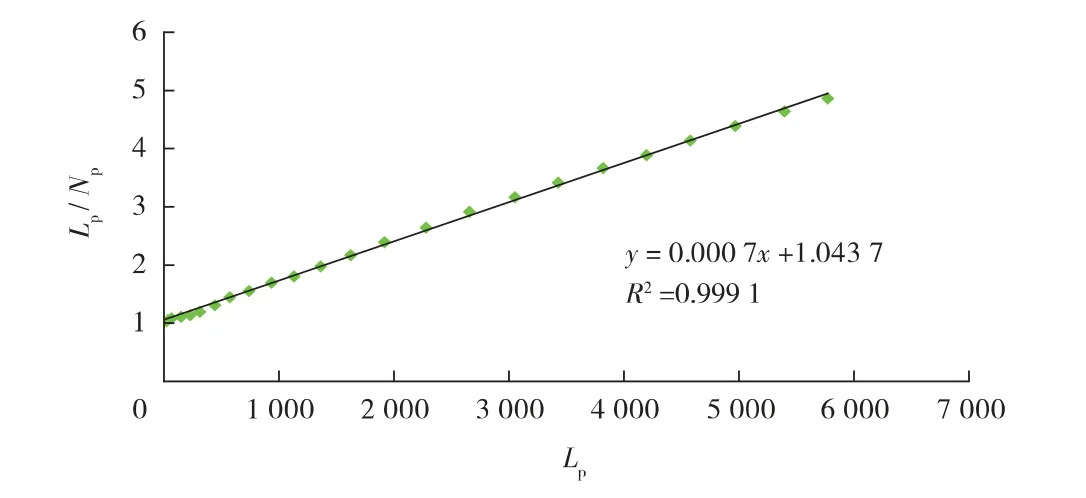
图3 丙型水驱曲线

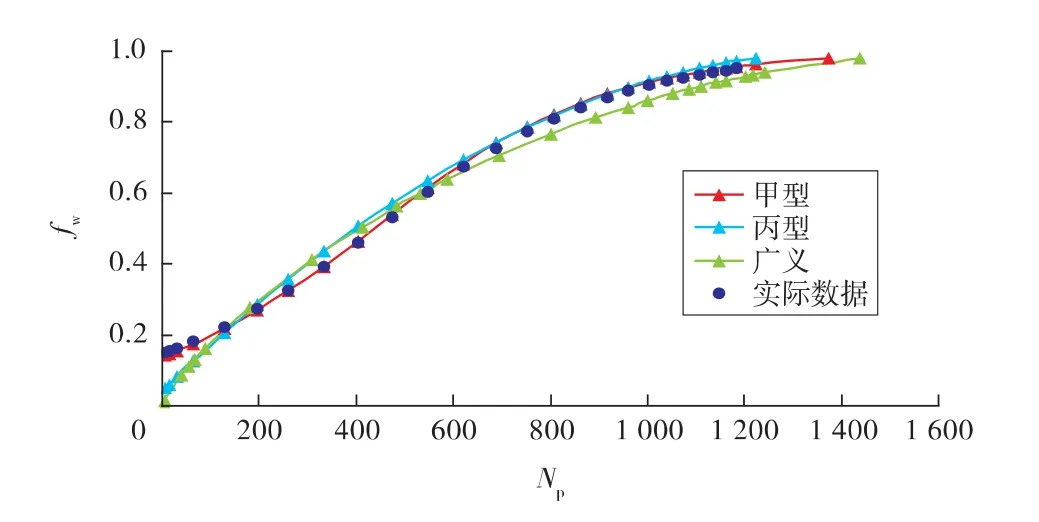
图4 3 种水驱曲线fw 与Np 关系预测

当油田含水达到极限含水率（fw=0.98）时，由式（8）、式（12）和式（16）得到广义、甲型和丙型水驱曲线预测的可采储量分别为1437×104，1375×104，1225×104t。由式（6）计算得出的最大可采储量为1 706×104t，明显偏大。应当指出，该最大可采储量无任何实际意义。

3 简要评论

通过研究、分析、推导和应用，对俞氏广义水驱曲线提出如下初步评论，谨供参考。

1）俞氏广义水驱曲线，并不广义。它是一种双对数直线关系的水驱曲线，只是众多水驱曲线中的一种，不能代表半对数坐标系统的水驱曲线，如甲型水驱曲线；也不能代表直角坐标系统的水驱曲线，如丙型水驱曲线。因此，将其称为广义水驱曲线有些言不符实。

2）俞氏广义水驱曲线的建立过程简单牵强，不够严格，引起人们的质疑实属必然。作为一种新型水驱曲线的提出，应当在正文或附录中进行充分的理论分析和推导，以便于读者的正确理解和应用。

3）在广义水驱曲线的基础上，文献［1］的作者直接提出了累计产油量和含水率的关系式。该关系式是俞氏广义水驱曲线的主要技术部分，未经任何推导就提出来了，怎么能让人信服呢？俞氏广义水驱曲线的关系式并不复杂，求导也比较容易，却无法得到俞氏的结果。请问俞氏为何不在文中正面交代清楚呢？更令人不解的是，文献［1］中没有出现广义水驱曲线的应用实例，甚至没有一张表示广义水驱曲线的图形。

4）在没有任何定义和说明的条件下，俞氏直接提出最大可采储量的确定方法，这是不可能为人所信服和接受的。尽管可通过假设经简化得出，但是它的不确定性和不可靠性是必然存在的。实际上，文献［1］中给出的俞氏最大可采储量没有任何实用价值。

5）实际应用表明，尽管3 种水驱曲线预测的可采储量比较接近，但因广义水驱曲线预测方法的建立存在不确定性、不可靠性和不合理性，必然会影响到该水驱曲线的可信度和实用性。正确的理论推导，才会得到正确的方法，正确的方法才能提供正确的预测结果。因此，计算方法的正确性和可靠性，是科技论文的核心和灵魂。文中用到的甲型和丙型水驱曲线及其预测方法，都是经过严格推导完成的，而广义水驱曲线的建立恰好缺少这一过程。

［1］俞启泰.一种广义水驱特征曲线［J］.石油勘探与开发，1998，25（5）：48-50.

［2］中国石油天然气总公司.SY/T5367—1998石油可采储量计算方法［S］．北京：石油工业出版社，1999：15.

［3］俞启泰.水驱特征曲线研究（一）［J］.新疆石油地质，1996，17（4）：364-369.

［4］俞 启 泰.水 驱 特 征 曲 线 研 究（二）［J］.新 疆 石 油 地 质，1997，18（1）：62-66.

［5］陈元千.水驱曲线关系式的推导［J］.石油学报，1985，6（2）：69-78.

［6］陈元千，郝明强，李飞.油气资源量评估方法的对比与评论［J］.断块油气田，2013，20（4）：448-453.

［7］陈元千，邹存友.水驱曲线法在油田开发评价中的应用［J］.断块油气田，2011，18（6）：769-771.

［8］陈元千，郭二鹏.预测水驱油田体积波及系数和可采储量的方法［J］.中国海上油气，2007，19（6）：387-389.

［9］陈元千.对纳扎罗夫确定可采储量经验公式的理论推导与应用［J］.石油勘探与开发，1995，22（3）：63-68.