基于粗糙集与遗传算法的储层识别技术
2014-06-17李铁军薛玲郭大立杜国峰许江文
李铁军,薛玲,郭大立,杜国峰,许江文
(1.西南石油大学研究生院,四川 成都610500;2.中国石油新疆油田公司勘探公司,新疆 克拉玛依834000)
在油气勘探过程中,利用测井、录井等技术采集的储层数据量较大,且数据信息具有严重的非正态性及多维性,如何挖掘其内在信息是后期储层综合评价的难点和关键。本文将粗糙集理论引入储层评价,通过对复杂的数据、信息进行分析推理,揭示其间的内在关系。利用布尔逻辑和粗糙集理论相结合的离散化算法[1],对训练样本集条件属性值进行离散化处理;将粗糙集理论与遗传算法相结合,进行知识约简;在此基础上,综合利用常规测井、核磁测井和录井数据,对储层含油气性进行识别。
1 理论基础
1.1 粗糙集基本概念
粗糙集理论是由波兰数学家Z.Pawlak 于1982年提出的一种数据分析理论,其主要思想是在保持分类能力不变的前提下,根据属性间的依赖关系,通过知识约简,导出问题的决策或分类规则[2-5]。
1.1.1 知识表达系统
知识表达系统可表示为S=(U,A,V,f),其中:U为论域,表示对象的非空有限集合;A 为属性集合,由条件属性集C 和决策属性集D 组成,A=C∪D,C∩D =Ø;V 为属性的值域集,对于∀a∈A,对应一个属性值域Va,因此;f 为信息函数,它为每个对象的每个属性赋予一个信息值,表示U×A→V,即∀a∈A,x∈U,存在f(x,a)∈V。
1.1.2 属性约简
属性约简是粗糙集理论的核心内容,其在保持知识分类能力不变的条件下,删除知识表达系统中不相关或不重要的属性,从而有助于快速作出正确的决策。属性约简的基础是属性间的相互关系,条件属性C 对决策属性D 的支持度kC(D)定义为
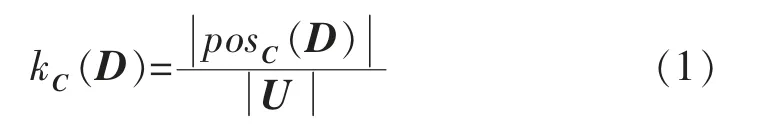
对于集合Q(Q⊆C),如果posQ(D)=posC(D),则称Q 是C 的一个D 约简。条件属性C 中所有D 必要的原始属性构成的集合,称为C 的D 核,简称相对核,记为coreD(C)。
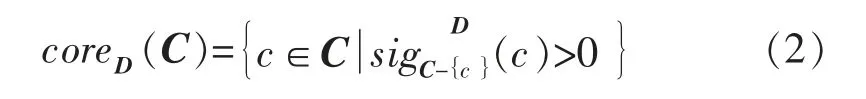
其中
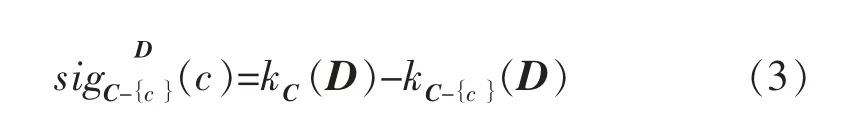
1.2 基于布尔逻辑的属性离散化算法
布尔逻辑与粗糙集理论相结合的离散化算法,是在不改变信息系统不可分辨关系的前提下,尽可能以最小数目的断点,对所有实例间的不可分辨关系进行区分。
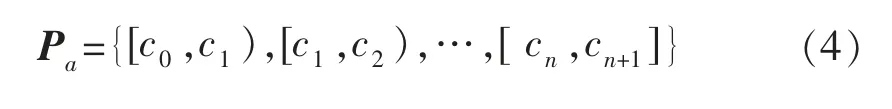
1.3 基于遗传算法的粗糙集属性约简
遗传算法[6]是一种自适应全局优化概率的搜索算法,具有全局优化和隐含并行性等优点,适用于粗糙集理论中属性约简问题的求解。求解最小约简的原则,一是属性约简的程度尽可能高,二是约简的条件属性对决策属性的支持度较高。由此确定约简算法的具体步骤为:
1)利用式(1),计算知识表达系统S=(U,A,V,f)中,条件属性C 对决策属性D 的支持度kC(D)。
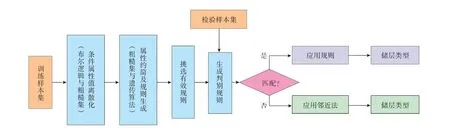
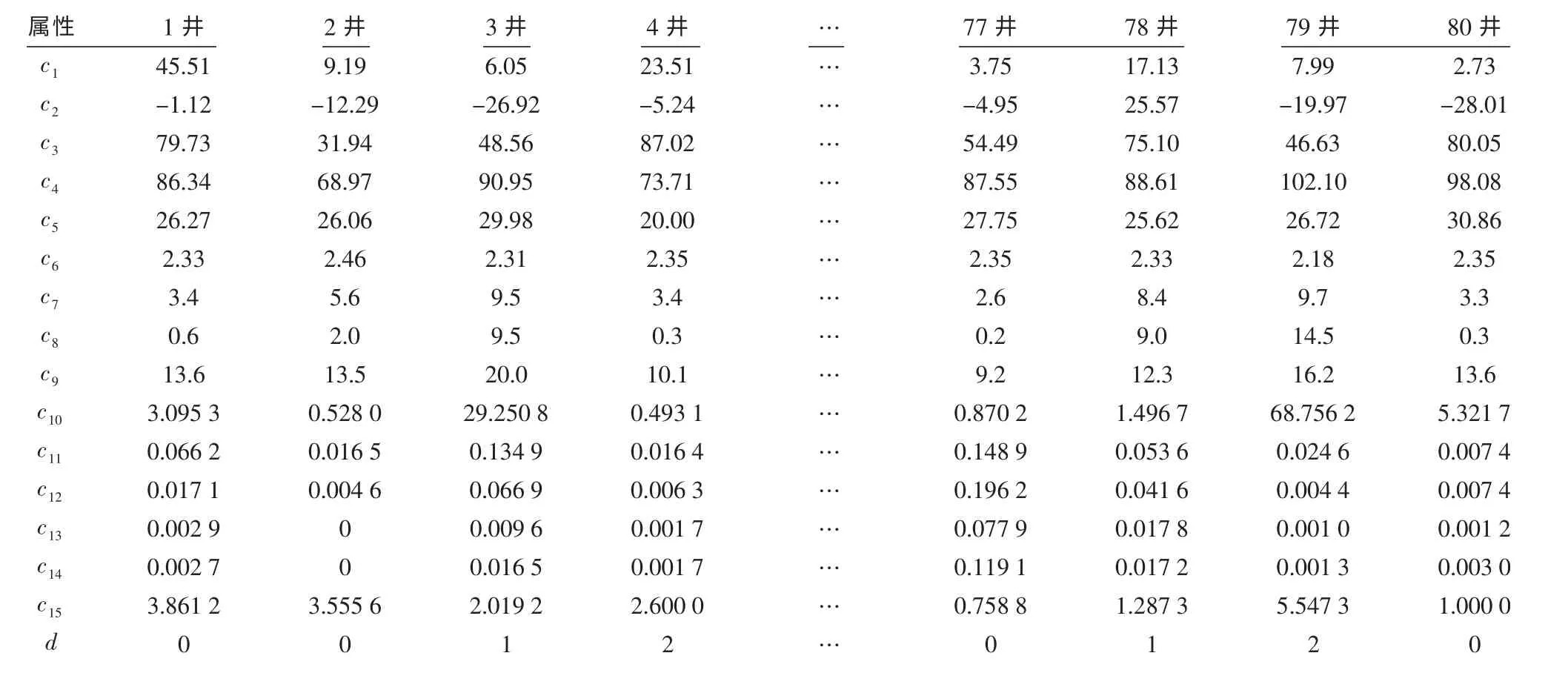
2)假设coreD(C)=Ø,对于每一个条件属性c∈C,利用式(3)计算其对决策属性D 的重要性若,则令coreD(C)=coreD(C)∪{c },最终得到C 对D 的相对核。当kcoreD(C)(D)=kC(D)时,coreD(C)即为最小约简;否则kcoreD(C)(D) 式中:β 为罚因子;α 为函数求解过程中设定的系数,α>0;sup(x)为支持度;sup0为预设的支持度。 4)利用轮盘赌方法选择种群中的个体,根据交叉概率pc和变异概率pm产生新一代群体,变异时保持核属性对应的基因位不发生变异。 其中,交叉概率pc和变异概率pm分别为 式中:k1,k2,k3,k4均为[0,1 ]的随机数;Fmax为群体中最大的适应值;Favg为群体的平均适应值;F′为要交叉个体中的最大适应值;F 为要变异个体的适应值。 5)依据最优个体保护策略,取每代种群中适应值最大的个体,原封不动地复制到下一代种群中,以保存最优个体。当最优个体的适应值不再提高时,终止计算,并输出最优个体,否则重新转步骤4)。 根据粗糙集理论,知识表达系统S=(U,A,V,f)经遗传算法约简后得到的每一个决策规则,是具有一定决策概率的不精确判别规则。对于∀x∈U,其对应的决策规则rx的价值,可采用支持度sup(rx)、置信度con(rx)和覆盖度cov(rx)等3 个指标进行衡量: 式中: C(x),D(x)分别为x 的C 等价类和D 等价类。 其中,支持度用于衡量决策规则的强度,反映了论域中支持此决策规则的对象占全体对象的比例; 置信度用于衡量规则中条件类分配到决策类中的精度,反映了决策规则的可信性; 覆盖度用于评估决策规则的质量,反映了决策规则的条件类对决策类的覆盖程度。 利用布尔逻辑和粗糙集理论相结合的离散化算法[1],对训练样本集条件属性值进行离散化处理; 运用基于遗传算法的粗糙集属性约简算法,提取储层评价规则;将检验样本与生成的规则进行匹配,若与规则匹配,则应用规则进行储层评价,否则应用最近相邻法进行储层评价。具体步骤如图1所示。 图1 储层识别流程 属性约简后得到的最小约简表为一组逻辑规则的集合,利用其对样本数据进行处理,得到决策规则。利用支持度、置信度和覆盖度等规则评价指标对生成的决策规则进行过滤,提取有效的储层识别规则集。利用判别规则对新检验样本进行储层识别时,可能出现4种匹配情况: 1)1 个新样本与1 个规则匹配,新样本的预测结果唯一。 2)1 个新样本与1 个以上的规则匹配,匹配规则的结果属性同属于1 个储层类型,预测结果亦唯一。 3)1 个新样本与1 个以上的规则匹配,匹配规则的结果属性不属于同一个储层类型。此时,为了对新样本的储层类型做出判断,采用多数优先推理方法消除冲突。即假设有2 条不一致的规则r1和r2,与1 个新样本匹配后,预测结果分别为γ1和γ2,此时若con(r1)=con(r2),则新样本的最终预测结果采用条件属性基数较大的规则的预测结果;若con(r1)≠con(r2),则当C(1) > C(2) ,con(r1)>con(r2) 时,新样本的最终预测结果选择γ1,当C(1) > C(2) ,con(r1) 4)一个新样本无法与任何规则进行匹配时,可采用最近相邻法进行储层类型的判别。设新样本x′ 的条件属性C= {c′1,c′2,…,c′t},则其与规则r 的距离l 可表示为1 式中:ki为属性c′i的权重,i=1,2,…,t;c′imax,c′imin分别为c′i的最大值和最小值。 设各属性的权重相同,选择d 值最小的规则所对应的储层类型作为新样本的预测结果。 选择新疆地区准东区块和西北缘区块具有常规测井、核磁测井及录井资料的126 口井进行研究。将参数不全及数据异常的井去除,最终利用其中的80 口井作为训练样本,19 口井作为模型的检验样本。借鉴国内前期的研究成果及储层识别参数的选择方法,从数据资料中53 种不同的参数属性中,选取地层电阻率(c1)、自然电位(c2)、自然伽马(c3)、声波时差(c4)、补偿中子(c5)、密度(c6)、可动流体孔隙度(c7)、渗透率(c8)、有效孔隙度(c9)、全烃增幅(c10),以及与地层中油气含量相关的气测五组分中C2/C1的增幅(c11)、C3/C1的增幅(c12)、iC4/C1的增幅(c13)、nC4/C1的增幅(c14)和C2/C3的增幅(c15)等15 个指标变量作为条件属性,构成条件属性集C={c1,c2,c3,…,c15},进行储层识别[8-20]。决策属性D 为产油量,根据储层是否达到工业油流标准,将储层分为干层、水层和油层,属性值分别用0,1,2 表示,即D={d=i,i=0,1,2}。 利用80 口井的15 个条件属性值和1 个决策属性值构建决策系统表(见表1),其中省略了部分井的数据。利用布尔逻辑和粗糙集理论相结合的离散化算法,对每个条件属性ci(i=1,2,…,15)进行离散化处理。例如,根据c1的离散点11.505 和23.025,将c1分为3 个离散区间,落在不同区间时的取值分别为0,1 和2。结合表1,得到离散后的决策信息系统表(见表2)。 利用基于粗糙集的遗传算法对属性数据进行约简,共产生432 条识别规则。其中,有些规则缺乏代表性与典型性。为此,按照置信度、覆盖度、支持度分别不小于80%,0.02,4 的标准,从中挑选出56 条规则,形成储层识别规则集,选择其中的10 条规则列于表3。 利用80 个训练样本得到的储层识别规则集,对19 个检验样本进行储层类型识别。结合2.2 中的储层评价判别方法,得出检验样本的最终预测结果。 表1 80 口研究井储层原始数据 表2 离散化后的储层数据 表3 储层识别规则 在此过程中,出现了4 种情况:1)有3 个检验样本与1 个规则匹配,识别结果唯一,其中1 个预测结果与实际不符,正确率为66.67%;2)有6 个检验样本与1个以上的规则匹配,识别结果为同一个储层类型,且预测结果与实际全部相符,正确率为100%;3)有7 个检验样本与1 个以上的规则匹配,识别结果为不同的储层类型,采用第3 种判别方法进行判别后,有2 个预测结果与实际不符,正确率为71.43%;4)有3 个样本不与任何规则匹配,采用第4 种判别方法进行判别后,有2 个预测结果与实际不符,正确率仅为33.33%。 在19 个检验样本中,16 个样本找到了与之相匹配的规则,匹配率为84.21%。将检验样本的最终预测结果与实际测试解释结果进行对比(见表4),可以看出,该储层识别方法预测油层的正确率较高。 表4 储层识别模型准确性分析 通过综合应用布尔逻辑、遗传算法及粗糙集理论,实现了基础数据的离散化处理、条件属性的约简,以及储层识别规则的提取,使得储层的含油气性识别变得简单易行,且识别的正确率较高,为油气层的进一步分析评价构建了必要的基础,对油气田开发方案的制定具有重要的指导作用。 [1]侯利娟,王国胤,聂能.粗糙集理论中的离散化问题[J].计算机科学,2000,27(12):89-94. [2]吕军,冯博琴,李波.基于遗传算法的属性约简[J].微电子学与计算机,2006,23(7):150-153. [3]李伟生,易哲.基于遗传算法的粗糙集属性约简算法[J].微电子学与计算机,2010,27 (3):71-74. [4]杨帆.粗糙集约简算法及其应用的研究[D].武汉:武汉科技大学,2005. [5]杨波,徐章艳,舒文豪.一种快速的Rough 集属性约简遗传算法[J].小型微型计算机系统,2012,33(1):140-144. [6]刘克文.基于GA 的神经网络设计及其应用[J].断块油气田,2000,7(4):41-42. [7]柯孔林,冯宗宪.基于粗糙集与遗传算法集成的企业短期贷款违约判别[J].系统工程理论与实践,2008,28(4):27-34. [8]于红岩,李洪奇,张万龙,等.敖南油田水平井测井解释方法研究[J].石油天然气学报,2012,34(1):84-87. [9]杨启明,高剑峰.多参数相关性分析在识别油气层中的应用[J].断块油气田,2000,7(3):44-45. [10]赵军.模糊灰关联分析法在测井识别油气水层中的应用[J].测井技术,2000,24(5):337-339. [11]何宏.气测录井检测评价油气储层技术研究[D].天津:天津大学,2003. [12]贾焕军.油气层神经网络识别方法研究[D].大庆:大庆石油学院,2003. [13]杨福成,光兴毅,张放东,等.锡林好来地区复杂储层测井综合识别及应用[J].断块油气田,2013,20(2):268-272. [14]杨思通,孙建孟,马建海,等.低孔低渗储层测录井资料油气识别方法[J].石油与天然气地质,2007,28(3):407-412. [15]孙娜.辽河油田滩海地区油气层识别及评价方法[J].断块油气田,2007,14(5):85-87. [16]姚美兰,王超,蒋恒丰,等.利用常规测井资料定性识别凝析油气层[J].油气田地面工程,2013,32(1):22-24. [17]李汉林,连承波,马士坤,等.基于气测资料的储层含油气性识别方法[J].中国石油大学学报:自然科学版,2006,30(4):21-23. [18]徐向阳.新疆塔北低阻油气层录井识别方法[J].海洋地质动态,2009,25(5):33-36. [19]王俊骏,桂志先,谢晓庆,等.苏里格气田储层识别敏感参数分析及应用[J].断块油气田,2013,20(2):175-177. [20]朱江华,李海波,潘丰.基于遗传算法和模糊粗糙集的知识约简[J].计算机仿真,2007,24(1):86-89.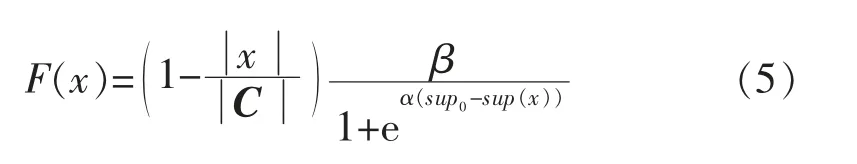
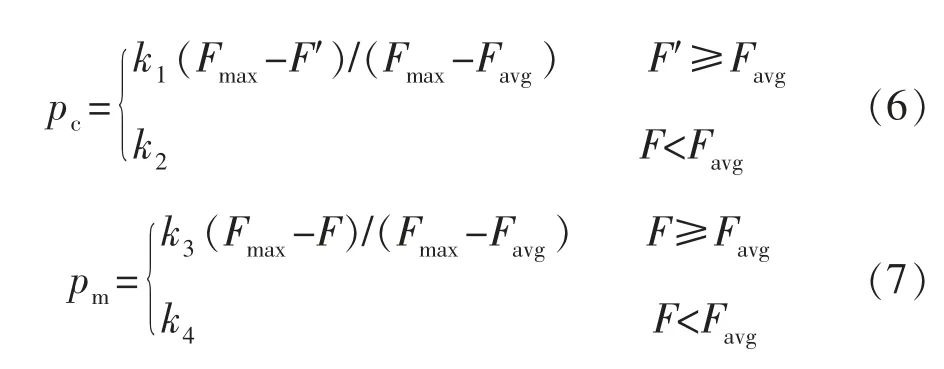
1.4 决策规则的评价
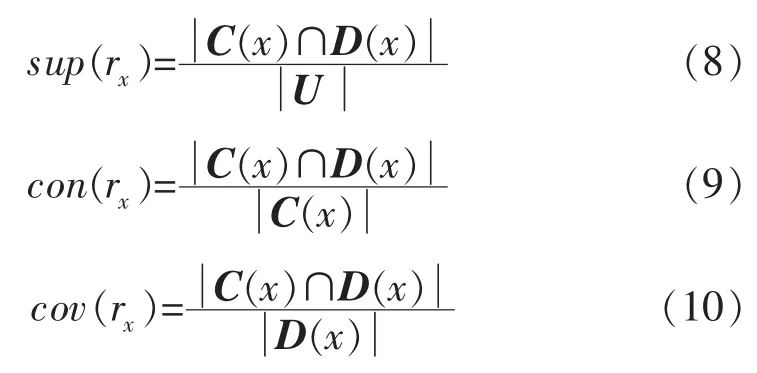
2 储层识别方法
2.1 识别模型的构建思路
2.2 储层的评价判别

3 实例应用
3.1 数据离散化
3.2 储层识别规则
3.3 模型预测准确性分析



4 结束语
