钢结构中高强螺栓连接的数值模拟方法

张文元，扈玥昕（1.结构工程灾变与控制教育部重点实验室（哈尔滨工业大学），150090哈尔滨；2.哈尔滨工业大学土木工程学院，150090哈尔滨；.云南大学城市建设与管理学院，650091昆明）

钢结构中高强螺栓连接的数值模拟方法

张文元1，2，扈玥昕3
（1.结构工程灾变与控制教育部重点实验室（哈尔滨工业大学），150090哈尔滨；2.哈尔滨工业大学土木工程学院，150090哈尔滨；3.云南大学城市建设与管理学院，650091昆明）

为能够对使用众多高强螺栓群拼接的钢结构大型复杂节点进行精确的有限元数值模拟分析，并揭示螺栓拼接节点在各阶段的受力性能，提出了一种以连接件单元代替螺栓的简化模拟方法.对高强螺栓单剪连接使用实体单元建模，并考虑各种非线性影响，进行精细的有限元模拟分析.在深入研究连接的弹性、滑移、强化和屈服等各个阶段受力机理的基础上，给出了代替螺栓连接件的本构关系，并将其成功应用于简化的壳单元连接模型中.针对工程中常用的不同规格连接进行了大量算例分析，并将简化模型与精细模型计算结果进行对比，验证了所提方法在高强螺栓拉剪连接有限元模拟中的可行性，为使用数值模拟方法揭示大型复杂螺栓群连接节点的真实受力状态奠定了基础.

钢结构；高强螺栓连接；数值模拟；有限元分析；本构关系

在大型钢结构?建筑中，为现场安装方便，在节点连接和构件拼接处大量使用高强螺栓，节点的螺栓群受力复杂，钢结构设计规范［1-2］中的计算方法及基本假定未必能够完全适用，特别是弹塑性阶段螺栓的受力性能及对节点的影响更加难以把握.因此为揭示各种复杂钢结构关键节点的受力性能，通常需要对这些复杂连接进行精细的有限元数值模拟分析.文献［3-5］表明，使用三维实体单元对螺栓连接节点的数值模拟时，能够较准确地反映螺栓的预紧力、摩擦、滑移、接触、屈服等线性和非线性特性，结果的准确性较高，甚至可以代替试验研究.但为了准确模拟栓杆和孔壁的力学行为，这种方法需要对螺栓和板件进行精细的实体元网格剖分，再加上螺母与板件、板件与板件、孔壁与栓杆之间的接触单元，会使螺栓群连接节点的有限元模型自由度数量巨大.同时螺栓连接中还存在较强的接触非线性、材料非线性和几何非线性，也为模型刚度方程的迭代求解带来了巨大难度.

为简化模型、提高计算效率，文献［6］提出利用壳单元来模拟螺栓拼接板件以及螺栓.文献［7］提出了运用桁架单元来模拟栓杆，用实体单元来模拟螺帽和螺母.文献［8］根据文献［9-10］的研究成果提出“隐形螺栓”的模拟方法.但上述方法精度不高，不方便使用，且很难模拟螺栓群连接的大型钢结构节点.本文在前人研究基础上，提出了一种简化、实用的螺栓连接数值模拟方法，使螺栓群的数值模拟成为可能.

1 单个螺栓连接的有限元精细化模拟分析

使用Abaqus通用有限元程序的实体单元对单个螺栓连接进行精细化建模，如图1所示，螺栓边距大于2倍螺栓直径，栓孔直径比栓杆大2 mm.在两块板件之间、栓帽与板件之间、栓杆与孔壁之间定义接触面，其法向为刚性无渗透，切向摩擦系数为0.4.对图1中的前面一块板的后端施加约束，确保其X方向不动，同时限制前面一块板的面外Z向变形，确保其能够在剪力作用下发生面内变形；后面一块板用于加载，不施加约束.这种边界约束不产生附加应力，符合工程中螺栓连接的受力状态.对后面一块板施加Z向（螺栓杆轴线方向）拉力和渐增的X向位移（剪力），板件克服摩擦力后将产生滑移，并逐渐使栓杆与孔壁接触，直至孔壁挤压屈服和栓杆剪切屈服.在螺栓和栓孔周围的重点关注区域，网格尺寸不超过5 mm，其他次要区域网格尺寸放大到10 mm.使用Bolt load功能定义螺栓截面上的预紧力，以荷载第一步形式施加.直径不超过30 mm和30 mm以上时的螺栓预紧力分别按文献［1-2］确定.

建立了板厚30～70 mm、栓径20～36 mm的9个模型，每个模型中螺栓的拉力分别取各自设计值的0、0.2、0.4、0.6、0.8和1.0倍，因此合计计算了45种情况.被连接板件的钢材统一取为大型钢结构中常用的Q345钢，高强螺栓统一取为10.9级.钢板和螺栓均采用双线性本构关系，弹性模量E=2.06×105MPa，切线模量按抗拉强度fu和对应的伸长率δ确定（螺栓fu=1 034 MPa，δ= 14%；被连接板件fu=470 MPa，δ=20%）.模型编号的定义方法为Pa-Mb-Tc，其中a为板件厚度、b为螺栓直径、c为螺栓拉力与设计值的百分比．

图1 采用实体单元的精细化模型

以模型P70-M36为例，图2给出了不同拉力作用下连接剪力与水平变形的计算结果，也给出了拉力为0的模型（T00模型）在几个关键时刻的应力和变形状态（下一小节中将详细论述）.可发现高强螺栓连接的剪力与变形曲线明显存在弹性、滑移、强化和屈服等几个阶段.随螺栓连接所受拉力的增大，抗剪承载力逐渐降低，但荷载位移曲线的形式十分接近，类似于弹性段缩短之后的向下平移，这与规范中拉剪螺栓相关公式的力学概念是一致的.其他规格的连接模型也均呈现出相同的规律，这为统一分析螺栓连接在不同拉力作用下的抗剪性能、归纳栓杆的本构关系提供了可能.

2 连接的受力特征和本构关系推导

根据图2中荷载位移曲线的刚度变化和各阶段栓杆与板件的应力特征，可以将剪力与位移曲线划分为0A、AB、BC、CD、DE 5个阶段，各阶段栓杆本构关系的推导如下．

2.1 螺栓无滑移时板件线弹性阶段（0A段）

对应着摩擦力克服之前的板件自身弹性变形阶段，此时被连接板件未产生相对滑移，依靠栓杆施加预紧力后在被连接板件间产生的摩擦力传递剪力，栓杆自身的弯曲和剪切变形极小，可忽略不计.此阶段的栓杆本身不传递剪力，这个过程能够在下文提出的壳单元简化模型中加以考虑，故此阶段不计入栓杆的本构关系.

2.2 板件滑移过程中栓杆弹性变形阶段（AB段）

初始状态A对应着摩擦力刚好被克服，板件开始滑移，带动栓杆产生弯曲和剪切变形.由于下一节的简化壳单元模型能够自行考虑板件之间的初始摩擦力，所以对于整个连接而言，本文推导的栓杆本构关系实质上是克服摩擦力产生滑移之后的剪力和变形之间的关系，如图3所示.AB阶段中栓杆端部承受初始预拉应力和弯曲应力共同作用，栓杆沿杆长各个截面上均存在剪应力．终点B对应着栓杆端部在拉力和弯矩共同作用下边缘纤维开始屈服，如图2（b）中B点的应力状态所示．

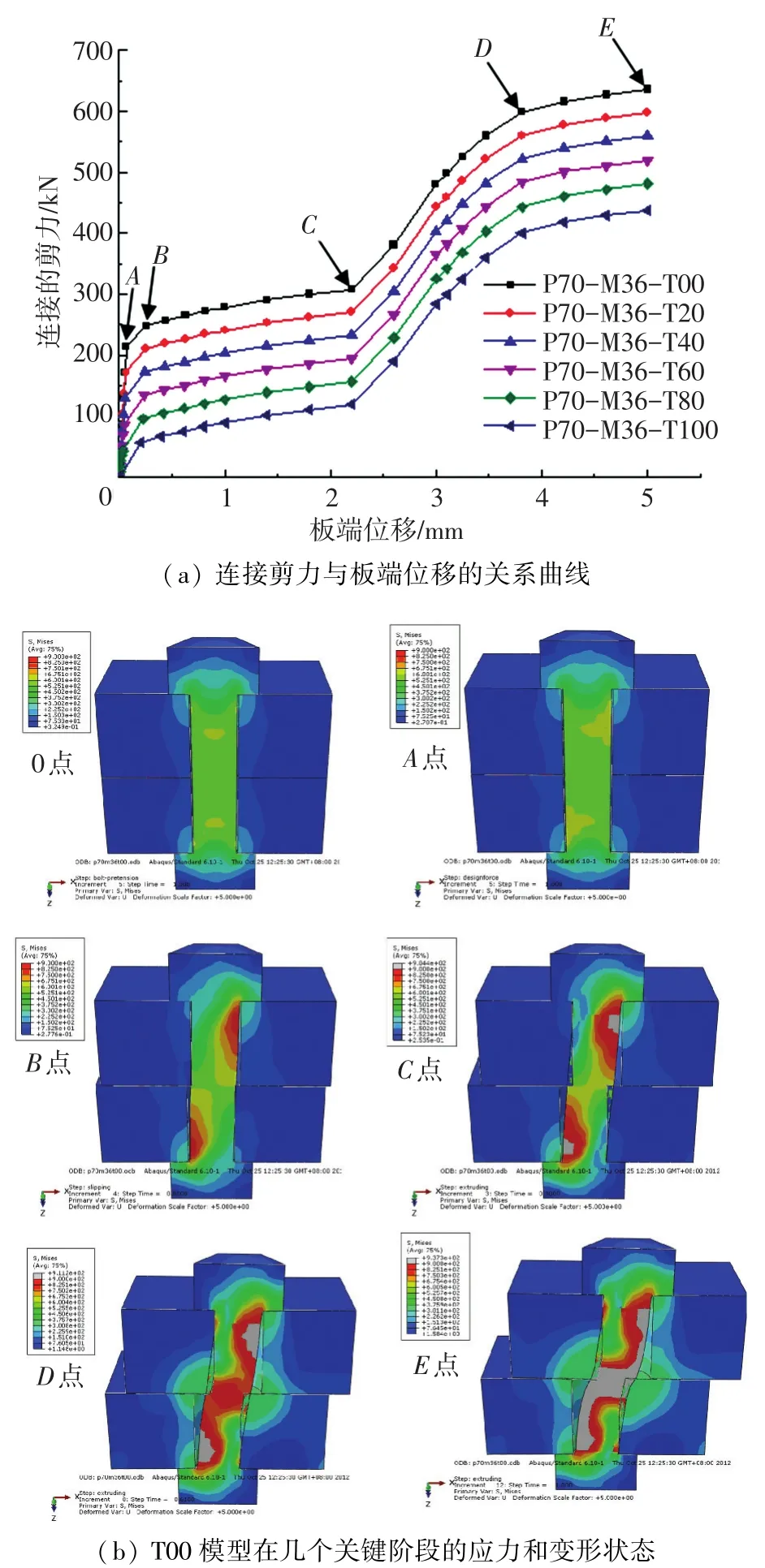
图2 连接剪力与位移曲线和关键阶段的应力状态

AB过程中栓杆一直处于弹性状态，其侧移刚度KAB可用结构力学方法计算得到，由栓杆的抗弯刚度Kb、剪切刚度Ks、栓杆侧移倾斜后轴向刚度的水平分量Ka、栓杆倾斜后摩擦力增大而造成的滑动刚度增量Kf等几部分构成．其中弯曲变形和剪切变形之和应该等于螺栓侧移，故Kb和Ks是串联的．它们串联后的刚度与其他几部分刚度并联，形成栓杆侧移的整体刚度KAB，如图4所示．

由此可得栓杆剪力与变形的关系为

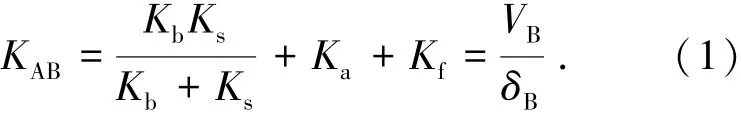
式中：δB为螺栓弹性侧移限值，VB为与之对应的栓杆弹性阶段的最大剪力．

图3 P70-M 36栓杆有侧移之后螺栓的本构关系

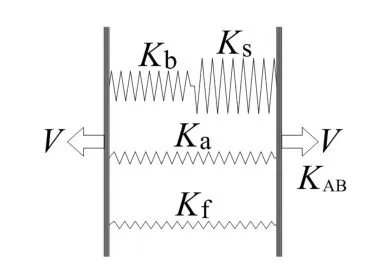
图4 栓杆在弹性变形阶段的侧移刚度组成

如图5（a）、（b）所示，栓杆在螺帽和螺母处不会产生转角，相当于有侧移的两端嵌固杆件，其抗弯刚度和抗剪刚度分别为：

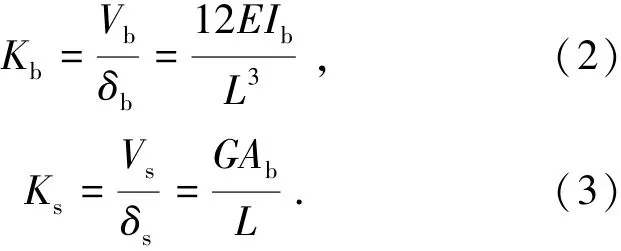
栓杆倾斜后长度增大，如图5（c）所示，会使栓杆的轴向拉力增大．当发生侧移δ后，根据几何关系容易算得螺栓的伸长量Δadd，并由此得到栓杆拉力的增量为

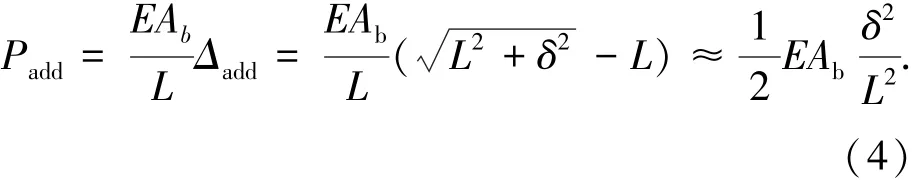
栓杆的真实拉力为上述拉力增量与螺栓预紧力P之和，其水平分量相当于一个刚度为Ka的弹簧产生的反力，即

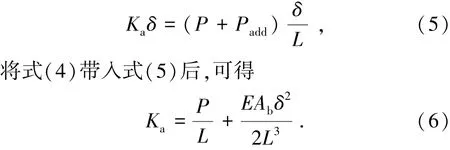
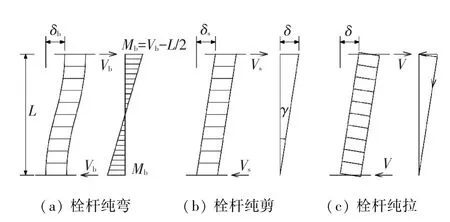
图5 栓杆在弹性阶段的受力及变形

式（6）中的第二项为栓杆拉力增量项，是δ／L的二阶无穷小量，若忽略它，则可简单地认为Ka仅与预紧力有关．

最后，栓杆倾斜伸长导致拉力增大，也增大了板件之间的摩擦力，其增量为

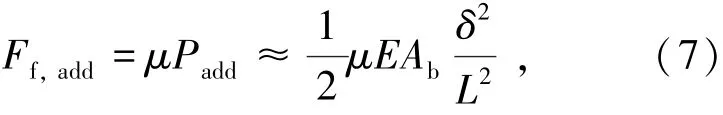
由此可以得到栓杆倾斜伸长后摩擦力增大而造成的滑动刚度增量Kf为

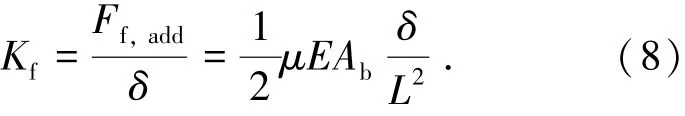
可以发现Kf与δ成正比，随栓杆侧移的增大，滑动摩擦刚度也相应增大．但Kf同时与L2成反比，故Kf在数值上一般较小，可以忽略．

至此，式（1）中栓杆侧移刚度的各个分量均已得到，下面确定B点坐标（δB，VB）．栓杆端部存在轴力和弯矩共同作用，边缘纤维达到屈服时（B点）：

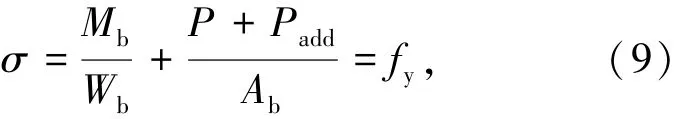
式中Wb为栓杆的抵抗矩．由图5（a）和式（2）可知栓杆端部弯矩将M和式b（4）一起代入式（9），可得

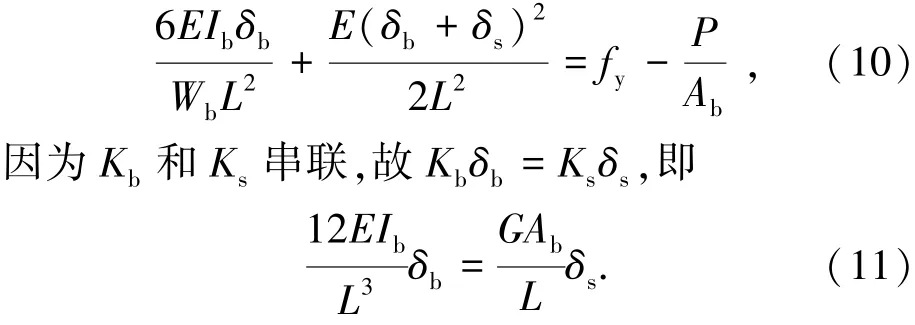
因此由式（10）、（11）可解得δb和δs，并忽略其中δ／L的高阶无穷小项，从而得到B点的侧移：

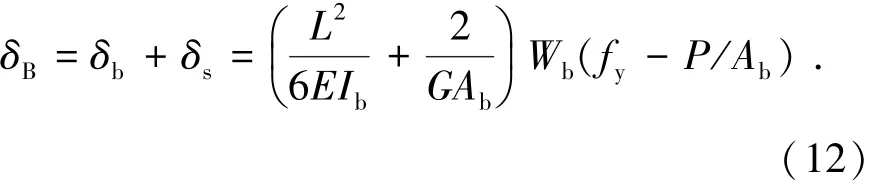
将式（12）代入式（1），可得B点所对应的剪力，由此定出了B点坐标．

2.3 板件滑移过程中的栓杆受弯屈服阶段（BC段）

随栓杆侧移的进一步增大，栓杆端部在拉力和弯矩作用下开始进入塑性，并逐渐向栓杆截面中心扩展，达到栓杆与孔壁发生接触时定义为C点，应力状态如图2（b）所示．本阶段栓杆同样以受弯和受剪为主，只是刚度随栓杆有效抗弯截面的减小而迅速退化．由于BC阶段摩擦力之外的剪力随侧移近似线性增加，如图2（a）所示，故可以用图3所示的一条直线近似模拟．由图6（a）的C时刻的几何关系可知，C点对应的位移δC为栓孔直径d0与栓杆直径d的差值，即

下面确定C点对应的剪力．由于C时刻在侧移产生的弯矩作用下，栓杆端部已有大部分截面发展了塑性，如图6（a）所示，可以认为栓杆端部弯矩近似等于塑性铰弯矩Mp，由此可得栓杆剪力V1=2Mp／L．同时栓杆倾斜、变长后栓杆轴向拉力会有一定增加，但由于此时栓杆端部发展了较多的塑性，弹性阶段的式（4）已不再适用．根据栓杆端部应力、应变分布特点，建议使用式（14）计算此时栓杆的附加轴力：

此时认为弹性区和塑性区各占一半面积Ab／2．式（14）的第一项代表侧移作用下弹性区附加轴力，是按式（4）得到的．式（14）中的第二项代表了塑性区应力强化的影响，缘于高强螺栓应力-应变曲线没有屈服平台，超过名义屈服点后应力仍会继续增加．其中强化系数α取1.1，相当于10.9级高强螺栓的强屈比，αfy-fy代表受拉区最外边缘屈服后应力增量．而且塑性区应力增量呈三角形分布，中和轴附近增量为0，因此取其平均值与塑性区面积的乘积作为栓杆塑性区强化后的轴力增量．这样，可得到由栓杆附加轴力Padd，C而引起的板件摩擦力增量V2=μPadd，C．

螺栓倾斜后的水平分力仍可由式（5）算得

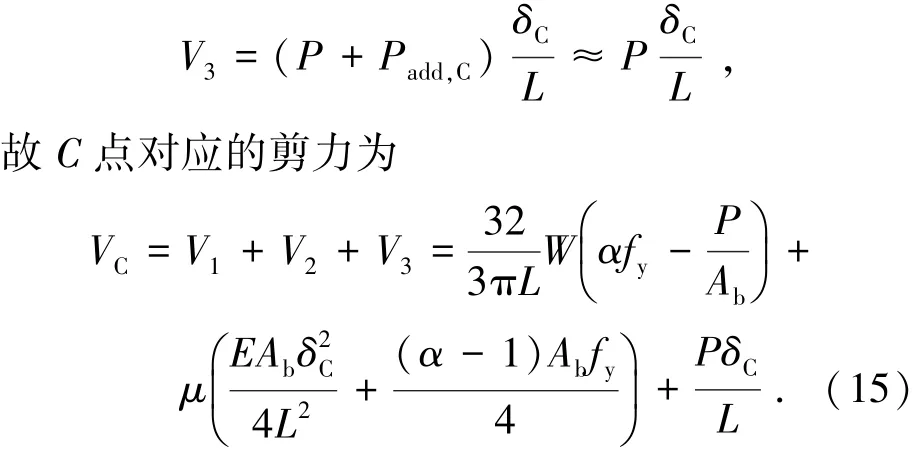
栓杆预拉应力会降低塑性铰弯矩，可认为栓杆轴力和弯矩呈线性相关，故（15）式中计算V1时使用了M=W（αf-P／A）=（αf-P／A）．ppybyb

2.4 孔壁在栓杆挤压下的屈服阶段（CD段）

从C时刻起，靠近栓杆跨中位置的孔壁开始与栓杆接触，随着侧移的增加，接触范围逐渐扩大.由于被连接板钢材的屈服强度远低于螺栓，孔壁会首先因挤压而发展塑性，如图6（b）所示，并逐渐进入强化阶段.同时挤压力使栓杆受剪，直至栓杆跨中剪切屈服，达到图2（b）中的D点．根据有限元结果，此时孔壁接触面塑性发展深度可达被连接板厚度的1／4～1／2.

CD阶段内，栓杆端部早已发生了较大的塑性转动，而栓杆其他部位尚在弹性范围之内，故栓杆的弹性弯曲和剪切变形与杆端的塑性转动引起的侧移相比可以忽略，此时栓杆可以近似为有一定侧移倾角的直线，如图6（b）所示．取孔壁接触面扩展深度为板件厚度的1／3时，根据几何关系，可以很容易求得D时刻的侧移为

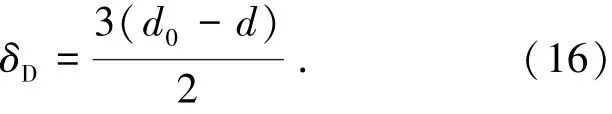
下面推导D时刻的剪力VD．达到D时刻，栓杆的跨中截面进入屈服，考虑到栓杆跨中受剪的同时还存在轴向拉力，故按Mises屈服条件可得屈服面方程：

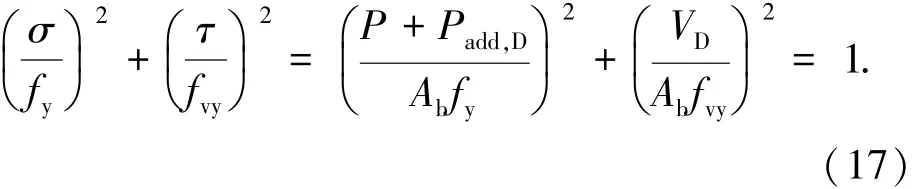
由于此时侧移已经很大，栓杆倾斜、应力强化后轴力的增大效应Padd，D予以考虑．计算Padd，D时式（4）、（14）均已不再适用，应根据D时刻栓杆端部应力、应变状态计算．此时栓杆端部绝大部分截面均已进入塑性，螺栓附加轴力均由材料应力强化引起．根据栓杆端部截面上应力强化的程度近似三角形分布的特点，取其平均值与栓杆截面塑性区面积（近似取0.7Ab）的乘积作为附加轴力：

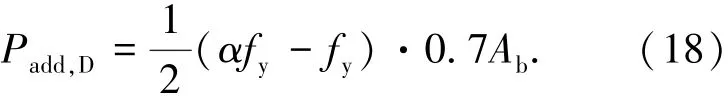
这个附加轴力由栓杆端部传递至栓杆跨中，故将式（18）代入式（17）后，可得D时刻的剪力VD．根据C、D的坐标亦可确定CD段的刚度KCD．

2.5 栓杆跨中截面上的受剪屈服阶段（DE段）

对于满足端距和边距等构造要求的厚板螺栓连接而言，当栓孔塑性变形和挤压应力达到一定程度，最终通常会体现为栓杆的剪断.跨中栓杆剪切屈服后，栓杆刚度降低很多，螺栓连接呈现出一定的滑移特性．因此，根据钢材的双线性模型，可以近似定义此时栓杆的剪切屈服刚度KDE为上一阶段刚度KCD的1%．则只要指定栓杆侧移量δE，很容易得到E时刻的剪力VE：

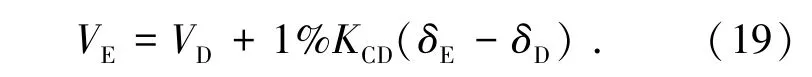
根据上述公式可推导出各种规格连接（不同板厚和不同螺栓直径）中栓杆受剪后的本构关系.例如，表1给出了P70-M36螺栓单剪连接的本构关系.

图6 C-D时刻栓杆的侧移和受力模式

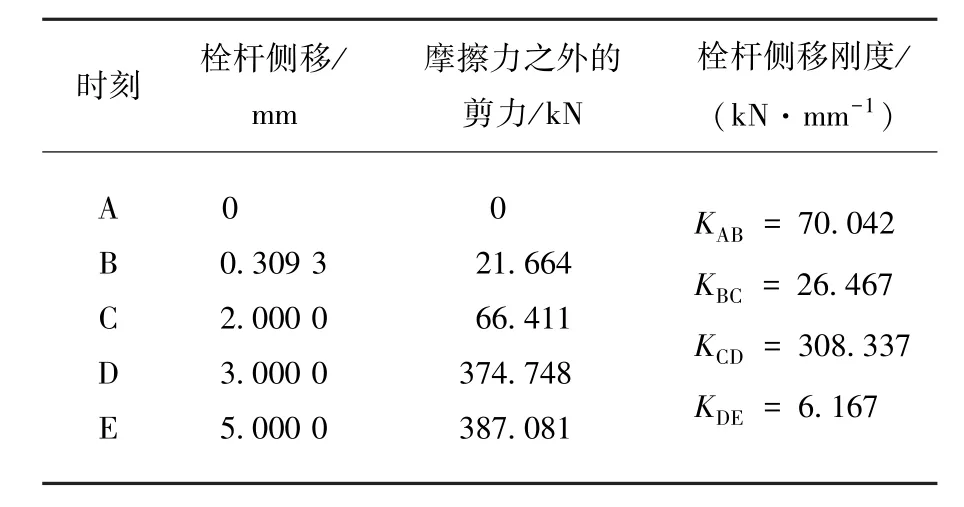
表1 P70-M 36螺栓单剪连接的本构关系

3 简化的壳单元模型及结果对比

在此使用壳单元模拟被连接板件、使用自定义本构关系的连接件模拟栓杆.单个螺栓连接的壳单元模型如图7所示，壳单元平面位于板件厚度的中面处.其边界条件和荷载均与第2节中的实体单元相同，栓孔附近网格加密，与实体单元模型类似.由于连接件无法直接施加螺栓预紧力，因此在螺母和螺帽范围内的被连接板面上，预先施加成对的面压力，成对的面压力自相平衡，以模拟螺栓预紧力对板件产生的预压力.如果连接还受到其他拉力作用，这些拉力将与预压力相互抵消，从而降低被连接板件之间的挤压力，使其抗滑移承载力降低，能够与拉剪螺栓的受力性能保持一致.

将上节得到的栓杆侧移与剪力的本构关系赋予设置在栓孔中心处的连接件，以模拟板件摩擦力克服后的栓杆受剪性能.模拟栓杆的连接件在Z向自由，不会传递被连接板件的面压力，其两端分别与受剪后会发生接触关系的栓孔边缘进行自由度耦合，如图7（c）所示.在两块被连接板之间定义考虑厚度影响的接触面，其切向的摩擦系数与实体单元模型相同，都取0.4；其法向为不可压缩的硬接触.

对不同板厚和螺栓直径的单剪连接，图8给出了使用壳单元简化模型的部分代表性计算结果，并与实体元精细模型结果进行对比.可以看出，使用壳单元模型、并用自定义本构的连接件代替栓杆，无论是在栓杆与孔壁接触之前的滑移阶段，还是在栓杆与孔壁接触之后的承压和栓杆受剪阶段，壳元简化模拟方法均具有较好的计算精度.即使连接所受的拉力不同，两种模型的计算结果依然十分接近.只是当板厚和螺栓直径较小时，在滑移段的壳元简化模拟结果略小于精细结果，但后期极限承载力结果依然吻合良好，这种误差可以看成是保守计算时的安全储备.

运用壳元简化模拟方法显著减少了单元数量和节点自由度，极大提高了计算效率.单元数量由精细模型的2.07万个减少为0.37万个，自由度数量由精细模型的7.2万个减小为1.5万个，计算时间由精细模型的1 600 s减小为200 s.

也可以看出，随着设计拉力的增大，螺栓连接在各个阶段的抗剪承载力均呈线性下降，这是由于外拉力使被连接板之间的预紧力降低，板面之间的摩擦力也随之降低.螺栓直径相同时，被连接板件厚度的变化对连接的抗剪承载力曲线的影响不大，螺栓直径是影响连接在各阶段承载力的主要因素.

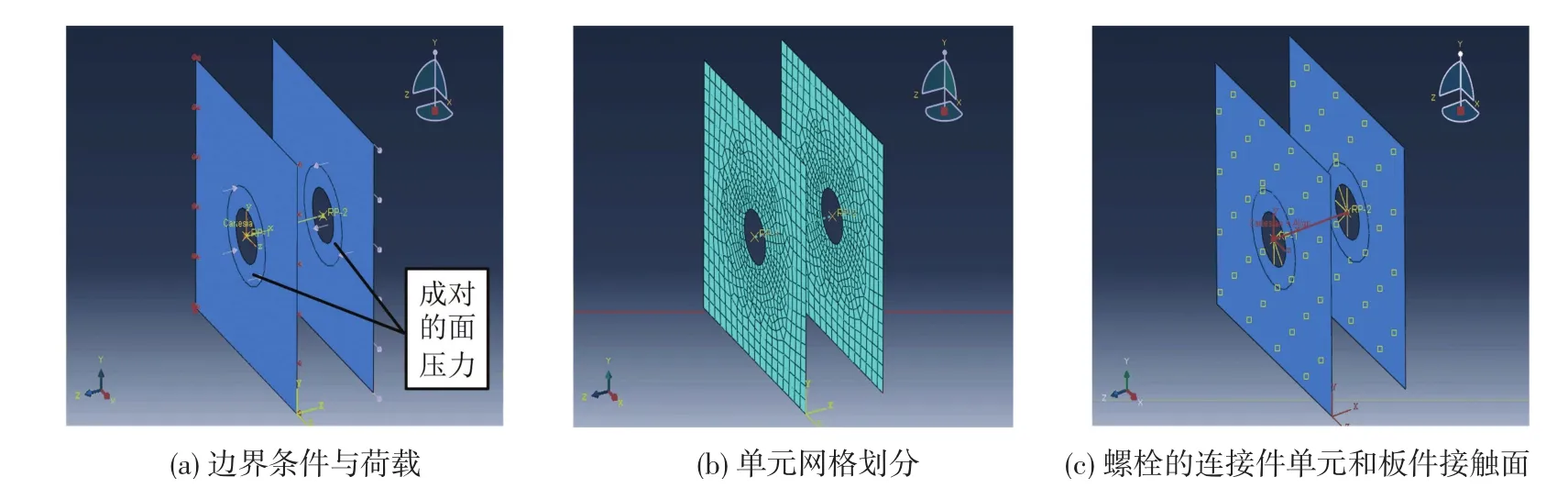
图7 螺栓连接模拟的壳单元模型

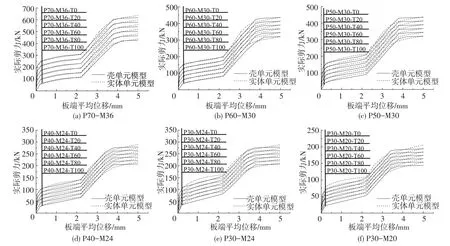
图8 不同规格螺栓连接时两种模型计算结果对比

4 结 论

1）通过精细的有限元模拟，发现高强螺栓连接的剪力与变形曲线明显存在弹性、滑移、强化和屈服等几个阶段，对每个阶段的受力状态都进行了明确定义，合理解释了螺栓的受力和破坏机理.

2）根据高强螺栓单剪连接在各阶段的传力机理，推导并提炼出栓杆真实受剪后（即滑移后）的本构关系，将其赋予代替栓杆的连接件单元，并成功应用于被连接板件的壳单元简化模型中，极大提高了计算效率.

3）使用精细的实体元模型和简化的壳单元模型，对不同板厚和螺栓直径的连接进行了大量对比分析，验证了所提模拟方法的有效性和可行性.这对使用数值模拟方法揭示复杂螺栓群连接节点的真实受力状态、提高设计水平和确保结构可靠度具有重要的理论意义和实用价值.

［1］GB50017—2003钢结构设计规范［S］.北京：中国计划出版社，2003.

［2］ANSI／AISC 360—10 Specification for Structural Steel Buildings［S］.Chicago（IL）：American Institute of Steel Construction，2010.

［3］MCCARTHY M A，MCCARTHY C T，LAWLOR V P，etal.Three-dimensional finite elementanalysis of singlebolt，single-lap composite bolted joints：part I-model development and validation［J］.Composite Structures， 2005，71（2）：140-158.

［4］MCCARTHY C T，MCCARTHY M A.Three-dimensional finite element analysis of single-bolt，single-lap composite bolted joints：Part II-effects of bolt-hole clearance［J］. Composite Structures，2005，71（2）：159-175.

［5］MCCARTHY C T，MCCARTHY M A，STANLEYW F，et al.Experiences with modeling friction in composite bolted joints［J］.Journal of Composite Materials，2005，39（21）：1881-1908.

［6］GRAY P J，MCCARTHY C T.A global bolted joint model for finite element analysis of load distributions in multi-bolt composite joints［J］.Composites Part B：Engineering，2010，41（4）：317-325.

［7］SHERBOURNE A N，BAHAARIM R.3D simulation of end-plate bolted connections［J］.Journal of Structural Engineering，1994，120（11）：3122-3136.

［8］RAZAVIH，ABOLMAALIA，GHASSEMIEH M.Invisible elastic bolt model concept for finite element analysis of bolted connections［J］.Journal of Constructional Steel Research，2007，63（5）：647-657.

［9］KUKRETIA R，BISWAS P.Finite element analysis to predict the cyclic hysteretic behavior and failure of endplate connections［J］.Computers＆Structures，1997，65（1）：127-147.

［10］KUKRETIA R，MURRAY TM，ABOLMAALIA.Endplate connection moment-rotation relationship［J］. Journal of Constructional Steel Research，1987，8：137-157.

（编辑 赵丽莹）

Numerical simulation method for high-strength bolt connections in steel structures

ZHANGWenyuan1，2，HU Yuexin3
（1.Key Lab of Structures Dynamic Behavior and Control（Harbin Institute of Technology），Ministry of Education，150090 Harbin，China；2.School of Civil Engineering，Harbin Institute of Technology，150090 Harbin，China；3.School of Urban Construction and Management，Yunnan University，650091 Kunming，China）

To proceed finite elementanalysis for bolted large-scale connection in steel structures and to explore the detailed behaviors under different loadings，a simplified method is brought forward，in which the highstrength bolt can be simulated by using connector element.The non-linear shearing performance of single-shear bolted connections is investigated with accuratemodels where the solid elements are employed.Basing on the mechanical properties in elastic，slipping，hardening，and yielding phase under shear force，a constitutive relation for the bolt connector is established and can be applied easily in shell elementmodel for the highstrength bolt connection.Large numbers of exampleswith varied parameters including plate thickness and bolt diameter are calculated respectively by using the simplified method with shell elements and the accurate method with solid elements.The result comparisons show that the simplified simulation method has a good computational efficiency and accuracy，and has a potential ability to simulate high-strength bolt connections. Keywords：steel structure；high-strength bolt connection；numerical simulation；finite element analysis；constitutive relation

TU391；TU313

A

0367-6234（2014）12-0008-07

2014-07-03.

国家自然科学基金（51178145）；《钢结构设计规范》国家标准管理组科研专项基金（GB500172010-20）.

张文元（1972—），男，教授，博士生导师.

张文元，hitzwy＠163.com.