非经典阻尼的位移输入模型和多点反应谱注记

柳国环，练继建，赵 悦

非经典阻尼的位移输入模型和多点反应谱注记

柳国环1，2，练继建1，2，赵 悦1，2

（1.天津大学水利工程仿真与安全国家重点实验室，300072天津；2.天津大学建筑工程学院，300072天津）

为注记和揭示底部单元为非经典阻尼下位移输入模型与多点反应谱的准确性与稳定性，本文涉及理论推导与计算分析两个层面.讨论了在时域模型中底部单元分别为经典与非经典阻尼的区别，在时域模型的基础上推导给出底部单元为非经典阻尼时多点反应谱公式，并通过算例验证.分析结果表明：底部单元为非经典阻尼时，位移输入模型不会出现底部单元刚度有关的阻尼项；理论上证明了在底部单元为非经典阻尼下位移输入模型和多点反应谱不存在结果不收敛问题；验证了底部单元为非经典阻尼下，采用位移输入模型计算结果的准确性和稳定性.

地震动；时域模型；位移输入模型；多点反应谱；非经典阻尼

地震反应谱理论由于考虑了结构的动力特性与地震特性之间的动力关系，又保持了原有的静力理论形式，因而反应谱理论在地震工程中得到广泛使用［1］.传统的反应谱理论为一致激励情况下的反应理论，它的主要优点在于形式简洁、概念清晰、应用方便，对于一般性结构，可取得较高精度结果，已为多个国家规范所采用［2］.然而，地震地面的运动往往具有不均匀性，在本质上是随空间变化的，由于波列传播速度的有限性和相干性的损失，以及局部场地地质的不同，会导致各支承点的地震激励出现显著差异［3］.因此地震动的多点输入模型与一致输入情形存在差别，这对于大跨结构而言更为明显.当前，地震动多点输入下的结构反应分析已成为抗震工程界的研究热点之一.其中，根据随机振动理论推导出的MSRS（multiple support response spectrum）理论表达式，计算快、方便使用，常用于工程结构设计中.

近年来，学者们在MSRS法方面做了许多研究.Yamamura等［4］将结构各支承点根据空间分布和场地地质情况分为若干组，假定每组支承点之间为完全相关，而组与组之间为不相关，在此基础上提出了一种近似的反应谱分析方法，该方法无法考虑行波效应和部分相干效应的影响.王君杰［5］推导出了一般阻尼结构体系在多维多点地震动作用下的结构响应的MSRS法.叶继红等［6］提出了基于虚拟激励原理建立了多点反应谱法，指出结构地震动反应由地面各点输入位移不一致引起的拟静力响应、地面加速度作用下引起的动力响应和二者之间的耦合项组成，具有公式形式简洁、物理意义明确、理论严谨的特点.本文作者也进行了相关研究，文献［7］全面详细地分析了位移输入模型存在底部单元计算结果的不稳定和不可靠，并提出了理论严格的附加无质量刚性元（AMCE）实效对策.文献［8］指出模型底部单元的耦合刚度其大小为底部单元刚度，直接决定于物理模型所对应的数值模型单元划分，这会导致计算结果不收敛.文献［8-9］处理问题方法的巧妙性在于没有引入地面运动的速度项，仍采用位移输入模型本身解决位移输入模型中存在不可忽视的问题.

本文对位移输入模型进行较为详细地分析与比较，明确指出在时域模型中采用底部单元为经典与非经典阻尼的差别；进而推导得出了底部单元为非经典阻尼在时域模型中表达式与多点反应谱中结构反应表达式，证明了底部单元为非经典阻尼时位移输入模型与多点反应谱不存在不收敛问题；最后，对底部单元为非经典阻尼的位移输入模型，结合算例进行了验证与说明.

1 理论简要回顾

在绝对坐标系下，一离散单元的结构体系与地面连接，将其自由度分为两类:n个非支座节点自由度与m个支座节点自由度．地震地面运动作用下，该体系的动力平衡方程可表达为

式中:M、C和K表示质量、阻尼和刚度矩阵；下标tt、uu和tu（ut）分别表示非支座节点、支座节点自由度及两者之间的耦合，大小分别为n×n、m× m、n×m（m×n）维；X、˙X和¨X为绝对坐标系下非支座节点的位移、速度和加速度反应列向量；U、˙U和¨U为绝对坐标系下支座节点的位移、速度和加速度反应列向量，即支座处地面运动向量；P为m维支座节点反力向量．

将式（1）中上式展开并考虑集中质量，可得到关于X、˙X和¨X的动力平衡方程:

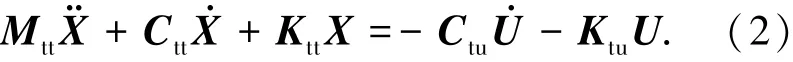
上式即为位移-速度输入模型.这时，将结构非支座节点的绝对位移分为两部分表达:

考虑拟静力位移Xs=-KttU=RU，R为影响矩阵．若将位移-速度模型式（2）中的阻尼项CtuU˙忽略:或

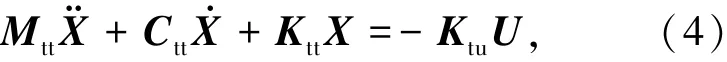
式（4）即为位移输入模型，式（5）为位移输入模型的等价表达式.

2 底部单元为经典与非经典阻尼模型差别的讨论与注记

底部单元为经典与非经典阻尼模型对比，如图1所示.在时域模型中，针对式（5）中的底部单元阻尼项，传统的方法选择采用经典阻尼中的Rayleigh阻尼（结构的阻尼矩阵是质量矩阵和刚度矩阵的线性组合），而本文引入的底部单元为非经典阻尼则是由自身性质所决定的.

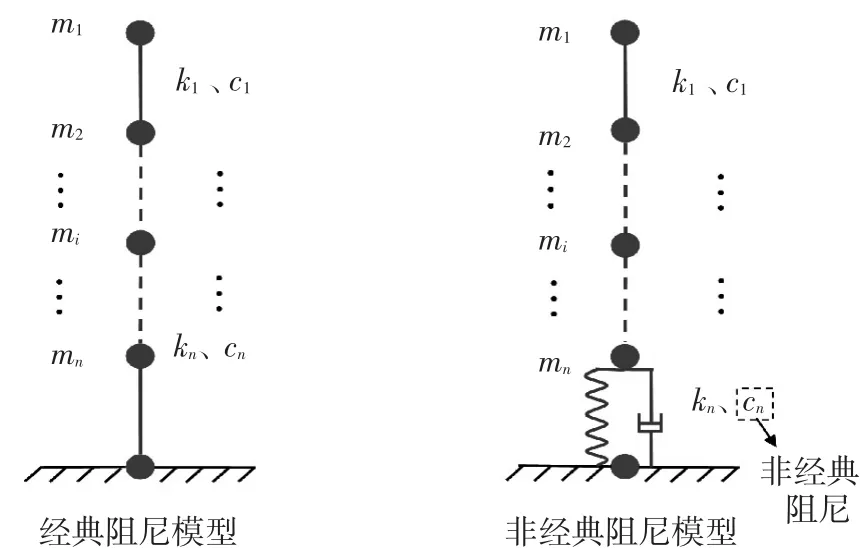
图1 经典阻尼与非经典阻尼对比

若考虑经典阻尼（以Rayleigh阻尼为例），C=αM+βK．

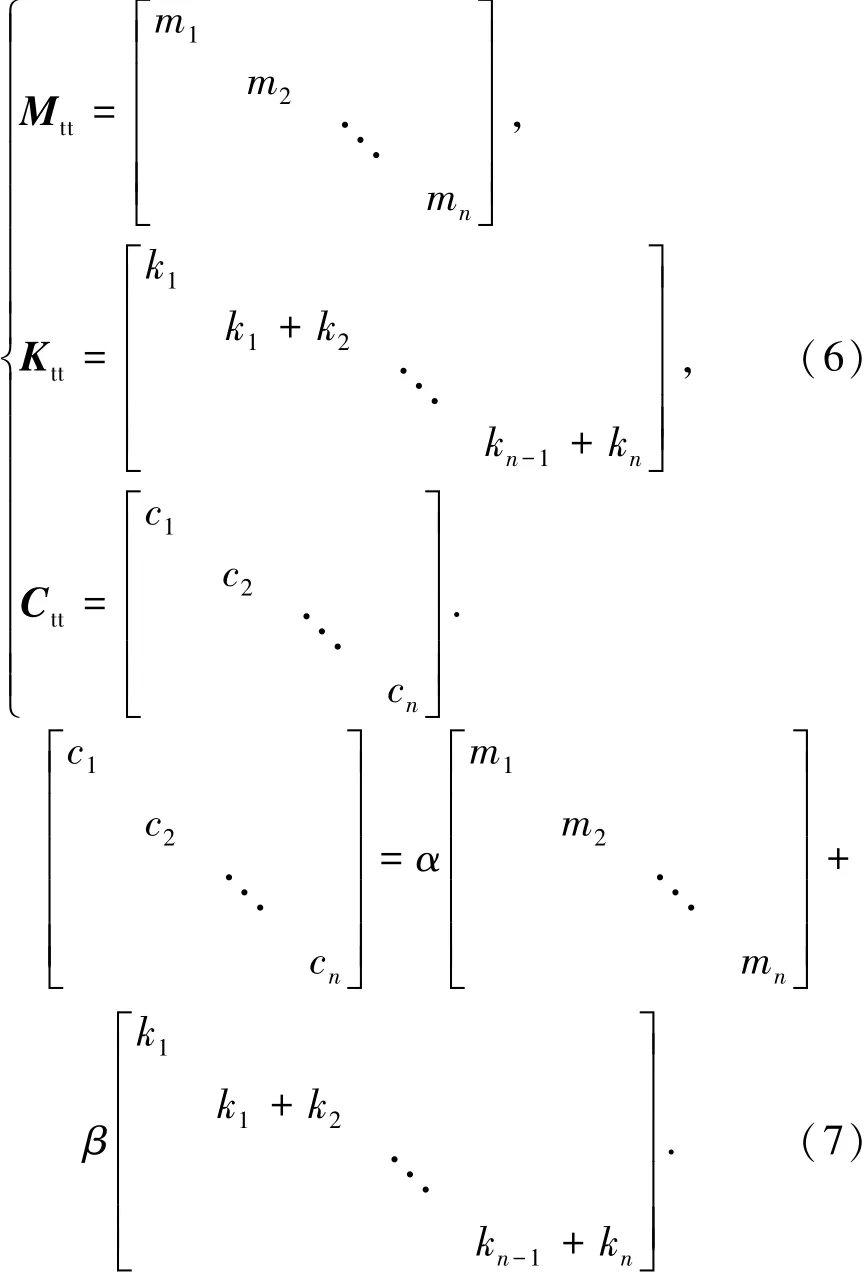
式中:m为集中质量，k为刚度系数，c为阻尼系数，α和β分别为Rayleigh阻尼的质量阻尼系数和刚度阻尼系数.

则式（5）可改写为

在经典阻尼下，基于位移输入模型导出的MSRS，存在不容忽视的问题，即底部单元内力随单元逐步细分出现不收敛不合理的现象，这是因为时域内位移输入模型本身右端存在βKtu˙U项所致．这点已在文献［8］中被充分证实与说明:模型底部单元的耦合刚度Ktu其大小为底部单元刚度，直接决定于物理模型所对应的数值模型单元划分，如随着底部单元数值模型单元划分得越密，会导致计算结果不收敛，表现为底部单元内力出现不合理的放大，与物理实际不相符．

若考虑底部单元为非经典阻尼，结构的阻尼矩阵C不能由质量矩阵M与刚度矩阵K线性表示．

则式（5）可改写为

对比式（8）和（10），可发现由于底部单元为非经典阻尼，式（10）等式右端不会出现βKtu˙U项，也就不存在刚度Ktu的影响，从而不会出现如经典阻尼所导致式（8）对应模型出现的上述不收敛等问题，符合实际物理模型，并具有严格的理论意义．

3 底部单元为非经典阻尼位移时域模型的结构反应表达式

本节基于文献［10-11］的思路，从位移输入模型推导底部单元为非经典阻尼时，结构时域反应计算公式.为得到多点反应谱表达式，需要对式（5）振

式中:ξi和ωi分别为第i阶振型的阻尼比和圆频时的Ctt为非经典阻尼；与之相对，若Ctt为经典阻尼（即Rayleigh阻尼），等式右端会出现项，就会出现2节中所讨论的问题．当在底部单元为非经典阻尼时，ξi包含了两部分:上部经典阻尼部分的ξi1与底部单元非经典阻尼部分的ξi2，即ξi1+ξi2．令

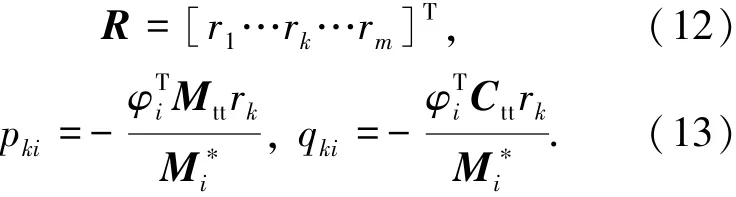
式中rk表示R的第k列向量．

将式（12）和（13）代入式（11）中，可得:

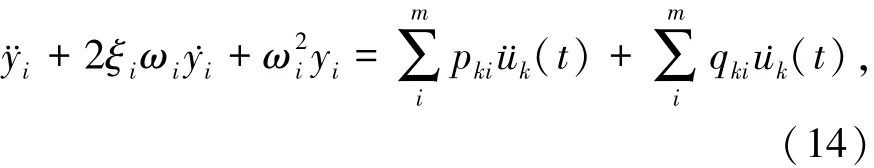
令

考虑阻尼比为ξi，圆频率为ωi的单位质量单自由度体系，分别受¨uk（t）和˙uk（t）激励，其运动方程可分别表示为:

根据有限元知识，结构反应（例如:内力、应力和应变），可表示如下:

式中系数ak、bk和ck可表示为

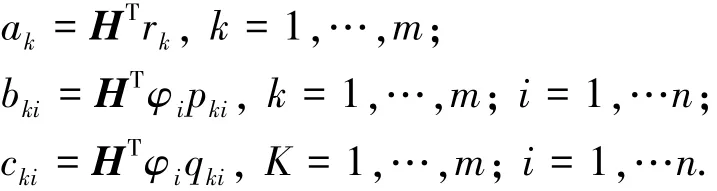
式中H表示反应转换向量，例如:刚度矩阵、应力矩阵和应变矩阵．为了指出系数ak、bki和cki在底部单元为经典与非经典阻尼的表达式的不同，表1给出了二者的对比．可以看出，系数ak、bki的表达式一样，cki的表达式不同，体现了二者的差异．

表1 系数在底部单元为经典与非经典阻尼表达式对比

4 底部单元为非经典阻尼时域模型对应的多点反应谱

4.1 底部单元为非经典阻尼位移输入模型对应的多点反应谱的表达式

基于3节中导出的式（22），本节根据随机振动理论，有下式成立:

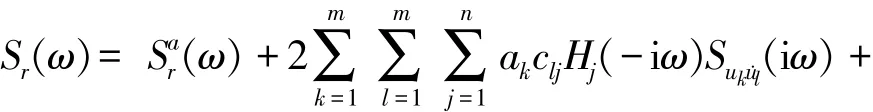
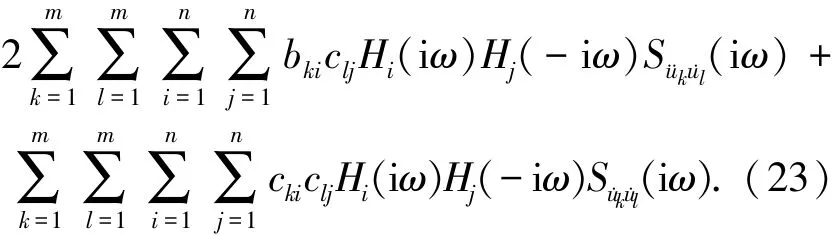
对式（23）两边在ω∈（-∞，+∞）上进行积分，可得到结构反应方差的表达式:

式中

式中Sukuk（ω）、S˙uk˙uk（ω）和S¨uk¨uk（ω）分别表示结构第k个支撑位置的地面运动的位移、速度和加速度功率谱密度函数．

表2 系数在底部单元为经典与非经典阻尼多点反应谱表达式中的对比

4.2 底部单元为非经典阻尼时位移与加速度输入多点反应谱差别的讨论

文献［10］已详细论述了对于经典阻尼结构体系下，位移输入模型的多点反应谱（D-MSRS）与加速度输入模型的多点反应谱（A-MSRS）区别.本节将在此基础上，讨论二者在底部单元为非经典阻尼结构体系下的差别.

式（23）为底部单元为非经典阻尼导出的DMSRS表达式.其与D-MSRS相比，不难发现两点:（1）由于加速度输入时域模型中，忽略等式右边的阻尼项，故右端不会出现Ctt项，体现在AMSRS中表现为cki=0，其中cki的具体表达式见表1，即可得A-MSRS多点反应谱表达式为式（24）；（2）由于加速度输入时域模型中，右端不出现Ctt项，在底部单元为非经典阻尼时，底部非经典阻尼项不会在该时域模型等式右端中出现，体现在A-MSRS中表现为仅体现在传递函数Hi．为了清晰起见，表3给出了二者之间的差别.后面的底部单元为非经典阻尼的算例将进一步说明.

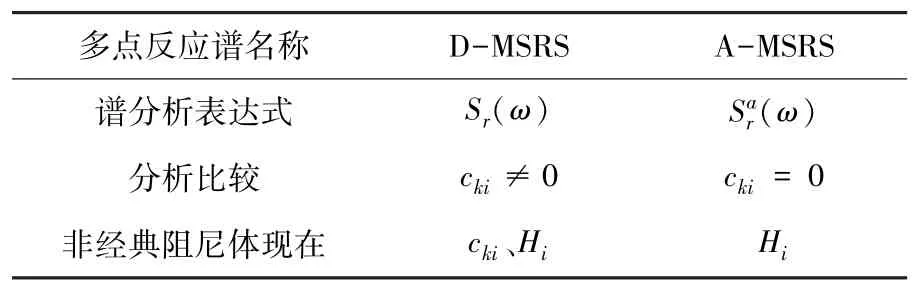
表3 两种多点反应谱表达式的对比

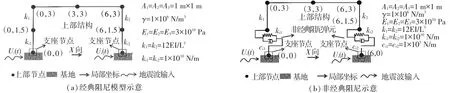
图2 算例模型示意

5 算例验证

5.1 算例与相关参数

第3节基于位移输入模型，推导给出了时域模型的表达式；第4节通过推导给出了底部单元为非经典阻尼多点反应谱的表达式（D-MSRS）.为验证时域位移输入模型理论分析的合理性，下面给出底部单元为非经典阻尼的算例，并与经典阻尼进行对比分析.

算例模型如图2所示，其中包括底部单元为经典阻尼模型和非经典阻尼模型.图2（a）为经典阻尼模型，底部单元为经典阻尼，采用Rayleigh阻尼；图2（b）为非经典阻尼模型，底部单元为非经典阻尼，采用非经典阻尼单元，阻尼为非经典阻尼单元确定.各个构件（包括单元刚度）、节点以及相关参数表示，所有参数均在SAP2000（V15.1.1新版本）中完成输入.方便起见，只考虑水平X向平动有效自由度，结构体系受到El Centro（1940NS）地震波的作用，地震地面加速度计录（Δt=0.02 s）与积分得到的地面运动位移时程如图3所示.

根据模型的前两阶圆频率ω1=3.104 rad／s和ω2=23.732 rad／s，以及振型阻尼比ξ1=ξ2= 0.05，可得Rayleigh阻尼的质量阻尼系数α= 1.745 3和刚度阻尼系数β=5.659×10-4.

图3 El Centro地震波加速度与位移时程曲线

5.2 底部单元为经典与非经典阻尼的时域位移输入模型验证与对比

本节目的主要有二:（1）通过算例进一步验证底部单元为非经典阻尼时，时域位移输入模型的合理性与稳定性；（2）通过对比底部单元为经典阻尼与非经典阻尼的时域位移输入模型，证明上述理论推导的严谨性.研究主要分3种底部单元长度（d=0.3，d=0.03，d=0.003，单位:m）情形，考察支座底部单元的剪力时程和标准差.

图4给出了在经典阻尼与底部单元为非经典阻尼情况下，采用位移输入模型对文中算例进行时程计算的结果.由图4（a）可以看出:随着底部单元的长度d越来越小，经典阻尼计算结果不同且差异较大，底部单元剪力出现不稳定不收敛，定性地证明本文2节所指出的问题.与之相比，图4（b）说明了底部单元为非经典阻尼计算结果的稳定性，底部单元剪力并未出现不收敛，计算结果与理论推导很好吻合.图5给出了在经典阻尼与底部单元为非经典阻尼情况下，采用一致加速度输入模型与位移输入模型对文中算例进行计算结果比较.由图5（a）可以看出:经典阻尼情况，以一致加速度输入模型为标准，位移输入模型与之相差很大，说明其计算结果具有不合理不稳定性.与之相比，图5（b）说明了底部单元为非经典阻尼计算结果的稳定性，一致加速度输入与位移输入的结果吻合得很好，进一步证明了其理论的合理性.

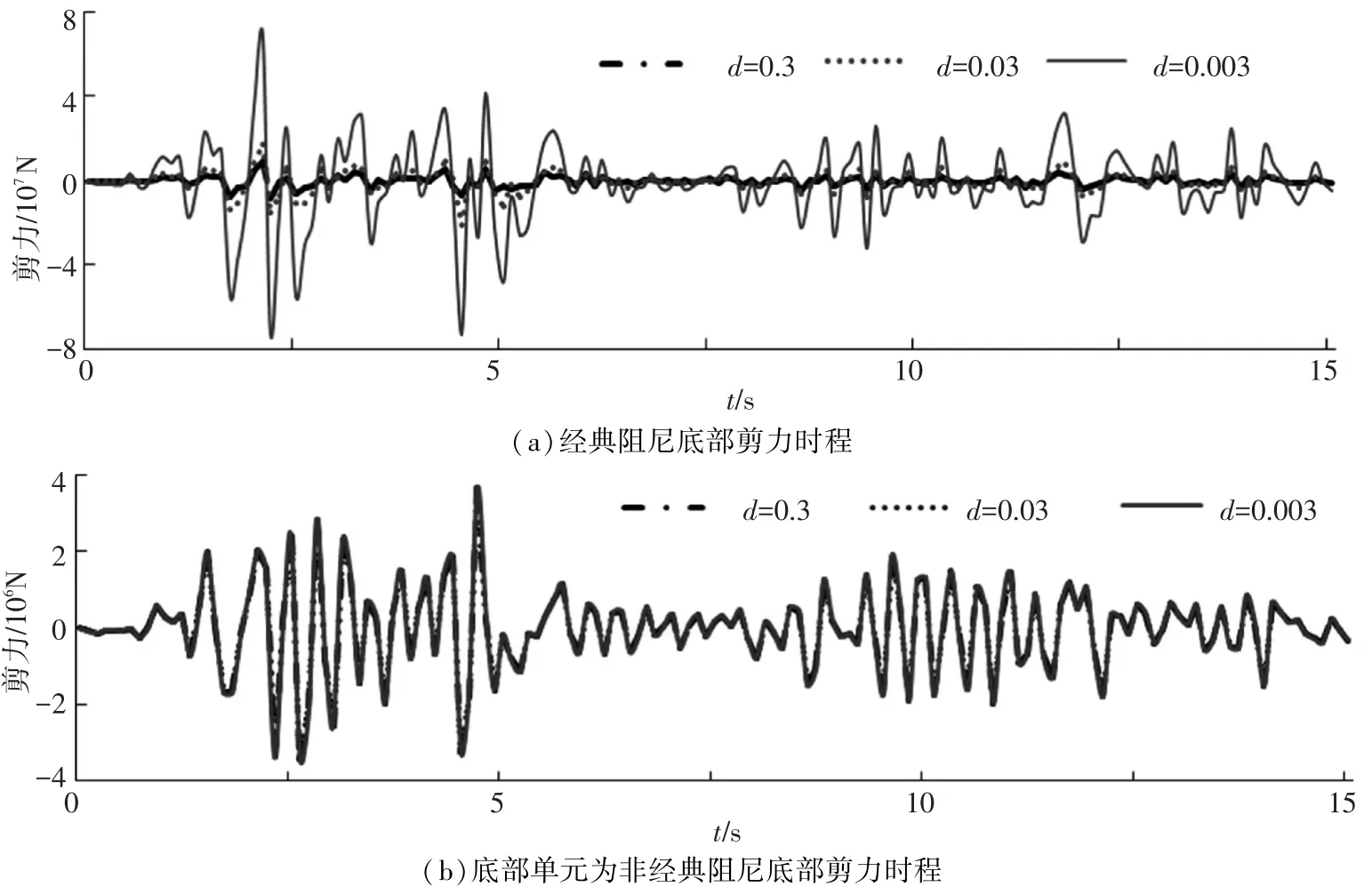
图4 不同底部单元长度的底部单元剪力时程

图5 两种阻尼类型加速度与位移模型的底部剪力时程对比

表4给出了两种阻尼的支座剪力的标准差与误差分析（以一致加速度为标准）.底部单元为经典阻尼的计算结果的误差分别为125%（d= 0.3），294%（d=0.03）和1 572%（d=0.003），定量地说明了其不可靠性与不稳定性，更进一步证明本文2节所指出的问题．与之相比，底部单元为非经典阻尼的计算结果的误差分别为0.362%（d=0.3），0.012%（d=0.03）和0.013%（d= 0.003）．这不仅说明本文讨论模型的有效性与准确性，也说明了其计算结果的合理性与稳定性，具有一定的工程借鉴意义．应该说明，本文之所以引用文献［7-8］所讨论的底部单元阻尼类型为经典阻尼时不可靠结果，目的是对比说明非经典阻尼时不存在相应现象．

此处，底部单元为非经典阻尼位移输入的时域模型理论分析与数值算例已经清晰且有力地说明了本文所指出的问题.同时，基于位移输入模型的多点反应谱理论公式已给出并证明，相关算例结果与时域模型类似，由于篇幅有限，不再繁冗陈述.

表4 采用两种阻尼类型的底部单元剪力的标准差与误差分析

6 结 论

1）针对底部单元为经典阻尼与非经典阻尼的位移输入模型区别进行了分析讨论，指出底部单元为非典阻尼时，位移输入模型不出现底部单元刚度相关的阻尼项，故底部单元剪力不存在不收敛问题，并证明了其理论上的合理性.

2）在时域模型的基础上，推导给出了底部单元为非经典阻尼的多点反应谱位移输入模型的表达式（D-MSRS），同时指出底部单元为非经典阻尼的D-MSRS与A-MSRS的异同.

3）最后，通过算例验证了底部单元为非经典阻尼下采用位移输入模型计算结果的有效性和稳定性，这一点不同于底部单元为经典阻尼的位移输入模型，具有工程借鉴意义.

［1］胡聿贤.地震工程学［M］.北京:地震出版社，2006.

［2］白凤龙，李宏男，王国新.多点输入下大跨结构反应谱分析方法研究进展［J］.地震工程与工程振动，2008，28（4）:35-42.

［3］CHOPRA A K.Dynamics of structures:theory and applications to earthquake engineering［M］.New York:Prentice Hall，2001.

［4］YAMAMURA N，TANAKA H.Response analysis of flexible MDF systems for multiple-support seismicexcitations［J］. Earthquake Engineering＆Structural Dynamics，1990，19:345-357.

［5］王君杰.多点多维地震动随机模型及结构的反应谱分析［D］.哈尔滨:国家地震局工程力学研究所，1992.

［6］叶继红，孙建梅.多点激励反应谱法的理论研究［J］.应用力学学报，2007，24（1）:47-53.

［7］柳国环，李宏男，国巍.求解结构地震响应位移输入模型存在的问题及其AMCE实效对策［J］.计算力学学报，2009（006）:862-869.

［8］柳国环，李宏男，国巍，等.求解结构地震响应位移输入模型中存在问题的一种新解决方法［J］.工程力学，2010（9）:55-62.

［9］柳国环，李宏男，田利.九江长江大桥在多点多维地震激励下的反应分析［J］.振动与冲击，2009，28（9）: 204-209.

［10］KIUREGHIAN A D，NEUENHOFER A.Response spectrum method for multi-support seismic excitations［J］.Earthquake Engineering＆Structural Dynamics，1992，21（8）:713-740.

［11］柳国环，李宏男，林海.结构地震响应计算模型的比较与分析［J］.工程力学，2009（2）:10-15.

［12］BERRAH M，KAUSEL E.Response spectrum analysis of structures subjected to spatially varying motions［J］. Earthquake Engineering＆Structural Dynamics，1992，21（6）:461-470.

［13］LIUGuohuan，GUO Wei，LI Hongnan.An effective and practical method for solving an unnegligible problem inherent in the current calculation model for multisupport seismic analysis of structures［J］.Science China（Technological Sciences），2010，53（7）:1774-1784.

［14］HAO Hong，OLIVEIRA C S，PENZIEN J.Multiplestation ground motion processing and simulation based on smart-1 arraydata［J］.Nuclear Engineering and Design，1989，111（3）:293-310.

［15］WILSON E L.Three-dimensional static and dynamic analysisofstructures:aphysicalapproachwith emphasis onearthquake engineering［M］.California: Computers and Structures，Inc.1998.

（编辑 赵丽莹）

Notes on displacement input model and multi-supported response spectrum of non-classical damping

LIU Guohuan1，2，LIAN Jijian1，2，ZHAO Yue1，2
（1.State Key Laboratory of Hydraulic Engineering Simulation and Safety，Tianjin University，300072 Tianjin，China；2.School of Civil Engineering，Tianjin University，300072 Tianjin，China）

To note and proclaim the accuracy and stability of displacement input model and multiple support response spectrum（MSRS）when non-classical damping in bottom element is adopted，this paper involves in two aspects-theoretical derivation and calculation analysis.The difference of time-domain model between classical and non-classical damping in bottom element is discussed.On the basis of time-domain model，the formula of MSRS is given and deduced，and it is verified by a numerical example.The derivation and analysis show that the stiffness-related damping term in bottom element does not appear in the displacement input model，the displacement input model and MSRS do not have problems of non-convergence，and the accuracy and stability of the displacement input mode is verified.

seismic ground motion；time-domain model；displacement input model；multiple support response spectrum（MSRS）；non-classical damping

P315.9

A

0367-6234（2014）06-0079-07

2014-01-13.

国家创新研究群体科学基金资助项目（51021004）；国家自然科学基金青年基金（51108466）；中国博士后科学基金（2011M500332）.

柳国环（1980—），男，博士，副教授；

练继建（1965—），男，博士生导师，长江学者特聘教授.

柳国环，liu-guohuan＠sina.com.