片空化状态下对转螺旋桨噪声特性仿真分析

王顺杰，王易川，戴卫国，李斌

片空化状态下对转螺旋桨噪声特性仿真分析

王顺杰，王易川，戴卫国，李斌

（海军潜艇学院，山东青岛266044）

为了研究对转螺旋桨空化噪声特性，利用Schnerr-sauer空化模型及RNG k-ε湍流模型，并采用动网格模型对对转螺旋桨进行空化数值分析。首先，对DTMB4381螺旋桨进行空化敞水性能计算，所得空泡形态与公开发表试验及数值模拟结果吻合较好。然后对对转螺旋桨空化噪声进行计算及分析，求解了不同监测点处的声压和声压功率谱密度。从计算结果可以看出噪声功率谱中存在着与前、后桨叶频相关的线谱成份。

片空化；对转螺旋桨；数值分析

1 引言

螺旋桨空化噪声是船舶辐射噪声的主要因素，常见的螺旋桨空泡主要有梢涡空泡、片空泡、云空泡、毂涡空泡等，由于空化物理问题的复杂性，多采用实验方法对空化现象进行研究[1-2]。随着CFD技术的发展，使用数值方法研究螺旋桨空化问题逐渐成为国际水动力学界的前沿和热点问题。而且对于声学问题的直接数值模拟，可以在任意场点上对噪声进行监测，有效避免了试验中水听器安装及其与流场之间的相互干扰问题。因此，数值计算将成为解决实际声学问题的一种重要方法。

刘登成等[3]利用RANS求解其采用非结构化网格对螺旋桨敞水性能和空泡性能进行了数值计算。杨琼方等[4]采用改进的Sauer空化模型和修正的SST湍流模型，分析研究了非均匀进流对螺旋桨空化水动力性能的影响。胡健等[5]用数值方法计算了螺旋桨的扰动速度，研究了螺旋桨尾流场的分布规律。Lindau等[6]用Kunz模型，和用UNCLE-M对螺旋桨P4831的空泡特性进行了分析，在较大范围的进速系数下，均预报出使推力系数和扭矩系数急剧减小的临界空泡数，并与试验结果吻合较好。

水下高速航行体普遍采用对转螺旋桨的推进方式。当其航速很高或未在大深度航行时，螺旋桨的局部空化常常不可避免。因此，研究对转螺旋桨空化噪声特性对于目标判别具有重要意义。目前，采用CFD技术对螺旋桨空化进行的研究主要集中在单桨方面，未见公开发表的利用CFD技术对对转螺旋桨空化噪声特性进行分析的相关文献。本文采用Schneer-sauer空泡模型及RNG k-ε湍流模型，利用动网格模型技术对对转螺旋桨进行空化噪声特性进行了数值分析。

2 数学模型

2.1 控制方程

假定气、液两相间无速度滑移，则气、液两相的连续方程和动量方程分别为：

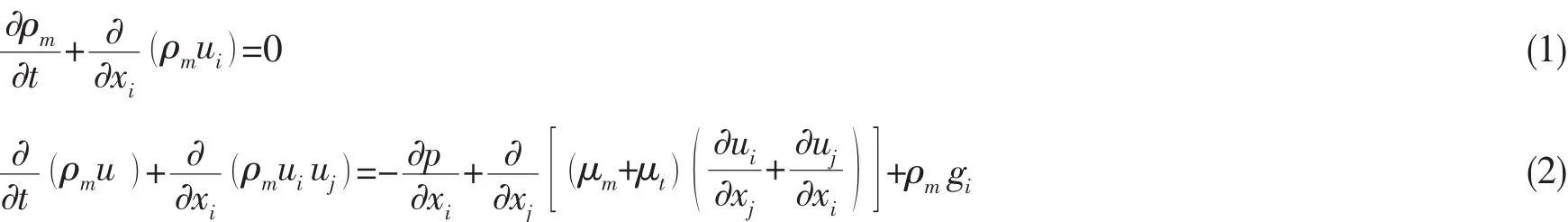
式中：m表示混合物，ρm为混合物密度，p为压力，ui为直角坐标系中绝对速度矢量的i分量，μm为混合物粘度，μt为湍流粘度。

2.2 Schnerr-sauer空化模型

采用Schnerr-sauer空化模型处理螺旋桨空化过程，并考虑相间滑移和水中未溶解气体对空化的影响，空化流动的连续性方程为：

水蒸气空泡相：

式中：ρv为水蒸气密度，a为水蒸气体积分数，Re和Rc分别为考虑蒸发和凝结的源项。根据Rayleigh-Plesset方程描述空泡的增长和溃灭过程，不同空化模型源项有不同的表达形式。

Schnerr-sauer空化模型为：

式中：ρl为液体密度，RB为空泡半径，pv为饱和蒸汽压。

2.3 RNG k-ε湍流模型

RNG k-ε湍流模型是基于重整化群的理论提出的，湍动能k和湍动耗散率ε的运输方程如下：

式中：湍流粘度μt=ρCuk2/ε，模型常数C2=1.68，Cu=0.085，σk=σε=0.717 9。β=0.012，η=Sk/ε，

与标准k-ε模型相比，RNG k-ε湍流模型通过修正湍流粘度，考虑了平均流动中的旋转及旋流流动情况，适用于强流线弯曲、漩涡和旋转流。

2.4 噪声模型

FLUENT中采用Ffowcs Williams和Hawkings提出的FW-H方程模拟声音的产生与传播，此方程中采用了Lighthill的声学近似模型。噪声模块的噪声处理主要采用FW-H式，该式由连续性方程与Navier-Stokes方程导出，具体形式如下：

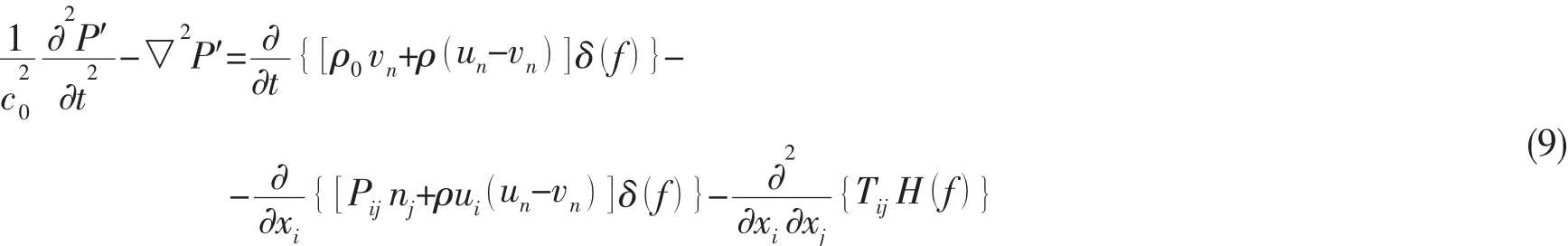
式中：ui为xi方向流体速度分量，un为垂直于面f=0的流体速度分量，vi为xi方向面运动速度分量，vn为垂直于面f=0的面运动速度分量，δ（f）为delta函数，H（f）为Heaviside函数，P′为远场声压（P′=P-P0），面f=0为源面，可为物体表面或具有渗透性的非物体表面，ni为指向外域（f＞0）的垂直单位矢量，c0为远场声速，Tij为Lighthill张力，定义为：

（9）式的推导利用了格林函数δ（g）/4πr，方程右边三项分别表示单极子、偶极子和四极子。该方程的解包括两个面积分和一个体积分，其中面积分反映了单极子、偶极子和部分四极子的贡献，而体积分反映了控制面外四极子的贡献。在水中声速比螺旋桨旋转速度大很多，因此四极子项可以被忽略，FLUENT中既如此，因此压力场求解式为：

3 数值方法验证

近年来，由泰勒水池（DTMB）提供的DTMB4381螺旋桨模型被大量研究者引用，作为检验其螺旋桨敞水性能及空化数值仿真方法的计算对象。据此，本文同样采用该螺旋桨模型作为检验数值仿真方法可靠性及计算精度的标准，同时，可以很方便地参考已公开发表的DTMB4381螺旋桨相关的文献制定计算策略。表1为DTMB4381螺旋桨模型的主要参数。

表1 DTMB4381桨模主要参数Tab.1 Main parameters of DTMB4381 propeller model

3.1 计算域及网格划分

计算区域设置来流段取3D（D为螺旋桨直径），去流段取7D，径向直径为4.2D。分为螺旋桨所在的旋转区域及其以外的固定区域两部分。使用GAMBIT软件对计算域进行网格划分，其中螺旋桨所在旋转区域采用非结构网格，固定区域则使用结构网格。将GAMBIT输出的网格文件导入到TGID中，对螺旋桨表面附近划分边界层网格，边界层网格类型为三棱柱。

图1 桨叶表面网格布置Fig.1 Mesh division of blade surface

3.2 边界条件

进口边界设为速度进口边界条件，出口边界设为压力边界条件。旋转区域与固定区域之间通过设置交界面完成两个区域之间的数据传递。采用FLUENT中提供的动网格模型控制旋转区域的网格按照给定螺旋桨转速整体运动，这种旋转区域整体运动的处理方式可以避免因网格重构造成的运动壁面附近较大的计算误差，同时也无需考虑因网格重构容易产生负体积对计算时间步长的限制。桨毂和桨叶设为壁面。

3.3 计算结果

依据国际船模水池会议的CFD不确定度分析临时规程[7]中收敛性研究，为进行网格收敛研究至少需要三套网格，并且各网格之间须满足一定的细化率要求。本文三种网格数量均是按照桨叶表面网格以0.7左右的比例进行细化，这组网格分别为Mesh1(1 488 654个网格)、Mesh2(2 236 952个网格)、Mesh3(3 240 491个网格)。

表2为取进速V=3.048 m/s，频率n=14.28 rps时对非定常条件下螺旋桨水动力性能进行模拟的推力系数KT、转矩系数KQ的计算结果与试验值[8]比较结果。定义收敛因子：

其中：εT32为Mesh3与Mesh2推力系数解之差，εT21为Mesh2与Mesh1推力系数解之差，εQ32为Mesh3与Mesh2转矩系数解之差，εQ21为Mesh2与Mesh1转矩系数解之差。

表2 推力系数KT和转矩系数KQ结果Tab.2 Calculation result of push coefficient KTand torque coeffiecient KQ

计算可得推力系数及转矩系数的收敛因子RKT=0.33、RKQ=0.72，由于两收敛因子均小于1，因此三套网格是单调收敛的，网格收敛性满足，即网格数量增加到一定时，RKT与RKQ数值解开始收敛，网格数再增加对计算结果影响较小。

图2为三种网格在进速系数J=0.7，空泡数σ=3.5条件下的螺旋桨叶面片空化大小的数值计算结果。图3（a）、（b）分别是Boswell[8]利用实验观察及Kim[9]数值计算得到的DTMB4381螺旋桨在该条件下桨叶表面空化情况，图3（a）中黑色区域代表发生空化的位置，图3（b）中桨叶白色区域代表发生空化的位置。通过比较可以看出，本文采用的三种网格对片空化位置的预报基本一致，但对片空化程度的预报不一致；网格Mesh1对片空化程度的预报与实验结果相差最大，Mesh2与Mesh3对片空化程度的预报与文献中的结果较为接近。

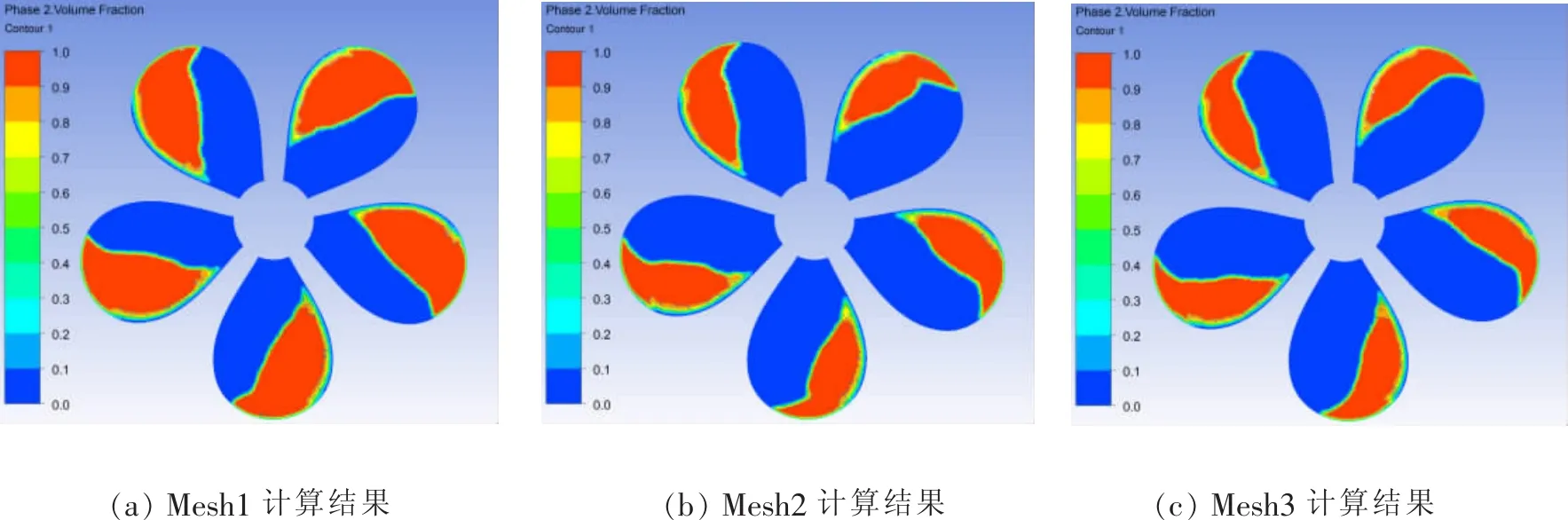
图2 螺旋桨空化数值计算结果Fig.2 Result of propeller cavitation numerical calculation

图3 Boswell试验及Kim计算得到的DTMB4381螺旋桨空泡图Fig.3 Pictures of DTMB4381 propeller cavity from Boswell’s experiment and Kim’s calculation

上述计算结果表明，采用RNG k-ε湍流模型配合Schnerr-sauer空化模型在合适的网格尺度下能准确地预报螺旋桨水动力性能及螺旋桨空化。虽然三种网格尺度均能较好地预报螺旋桨的水动力性能，但考虑到Mesh3预报的的水动力性能误差最小且所用的网格尺度能很好地模拟空化区域，因而后文中对对转螺旋桨片空化状态下的噪声特性仿真分析以Mesh3的网格尺度为标准划分网格。

4 对转螺旋桨片空化状态下噪声特性分析

本文所采用对转螺旋桨的主要参数如表3所示，其模型如图4所示。考虑对转桨的主要用途，在对转桨前方布置一航行体。设置来流段为2倍航行体长度，去流段为5倍航行体长度，圆柱半径为12倍航行体半径。对转桨区域的网格划分按第2节中Mesh3的网格大小进行，整个计算域网格总量为5 143 322。

前、后螺旋桨的转速均为n=33 rps，来流速度V=43 kns，通过调节出口压力控制空化数，使对转桨发生片空化。图6、图7即为前、后桨发生空化的区域。

本文利用FLUENT14.0中的声学计算模块Acoustics-Ffowcs-Williams&Hawkings进行声场分析，FW-H方程由连续方程与Navier-Stokes方程导出。首先存储足够多的时间步长上的测量点的压力脉动值，作为声场计算的声源项输入，可得到该点的声压值随时间的变化。对此声压时间序列做FFT变换，即可得到功率谱密度在频率上的变化情况。同时，为便于分析对转螺旋桨空化噪声的声场分布等特性，在噪声模块中设置了6个声压监测点，监测点的位置如图8所示。

图4 对转螺旋桨模型Fig.4 Counter-rotation propeller model

图5 桨叶表面网格布置Fig.5 Mesh division of blade surface

图6 前桨空化区域示意图Fig.6 Sketch map of front propeller cavitation area

图7 后桨空化区域示意图Fig.7 Sketch map of rear propeller cavitation area

4.1 噪声声压脉动特性

图9至图12为1、2、4、5号监测点的声压脉动图。从图中可以看出，监测点1、2具有相同的声压变化规律，其幅值随着距离的增加不断减小；监测点4、5具有相同的声压变化规律，其幅值随着距离的增加不断减小。

4.2 噪声声压功率谱特性分析

前、后桨转速均为33 rps，因此前桨叶频F1=198 Hz，后桨叶频F2=231 Hz。分别观察6个点在0-1 200 Hz频率范围内的功率谱特性。其中监测点1-3均具有图13（a）、（b）所示的1号监测点的功率谱密度分布。从图13（a）中可以看出396 Hz=2F1和462 Hz=2F2频率对应的功率谱密度最大，另外从图13（b）中可以看出在198 Hz=F1，231 Hz=F2，660 Hz=F1+2F2，825 Hz=3F1+F2，792 Hz=4F2，1 056 Hz=3F1+2F2，1 089 Hz=2F1+3F2处存在7条较为明显的与前、后桨叶频相关线谱。监测点4-6均具有图14（a）、（b）所示的4号监测点的功率谱密度分布。从图中可以看出在198 Hz=F1、231 Hz=F2、429 Hz=F1+F2、594 Hz=3F1、627 Hz=2F1+F2、858 Hz=2F1+2F2、891 Hz= F1+3F2、1 122 Hz=F1+4F2处存在8条较为明显的与前、后桨叶频相关线谱。因此，在对转螺旋桨空化噪声功率谱中存在着前桨叶频线谱成份、后桨叶频线谱成份以及前、后螺旋桨共同作用下的线谱成份。

图8 监测点布置图Fig.8 Picture of monitor layout

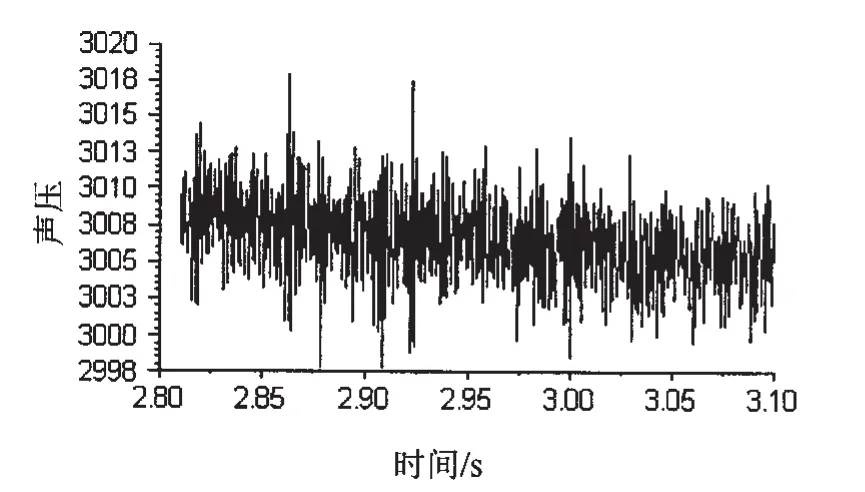
图9 监测点1的声压脉动图Fig.9 Acoustic pressure pulse at monitor 1

图10 监测点2的声压脉动图Fig.10 Acoustic pressure pulse at monitor 2

图11 监测点4的声压脉动图Fig.11 Acoustic pressure pulse at monitor 4

图12 监测点5的声压脉动图Fig.12 Acoustic pressure pulse at monitor 5

图13 1号监测点功率谱密度Fig.13 Power spectral density at monitor 1

图14 4号监测点功率谱密度Fig.14 Power spectral density at monitor 4

5 结论

本文利用计算流体力学方法对对转螺旋桨空化噪声进行了数值计算。计算时，采用的Schneersauer空泡模型、RNG k-ε湍流模型及动网格技术模拟螺旋桨空化，通过本文研究，可得以下结论：

（1）Schnerr-sauer空化模型及RNG k-ε湍流模型的组合方式可以较好地模拟螺旋桨桨叶表面空化问题。

（2）在对转螺旋桨空化噪声功率谱中存在着前桨叶频线谱成份、后桨叶频线谱成份以及前、后螺旋桨共同作用下的线谱成份。该线谱成分可用公式fk，m=kB1f1+mB2f2，其中B1、B2分别为前、后桨叶片数、f1、f2分别为前、后桨轴频，为今后利用该特点对水下高速目标进行判别打下了基础。

[1]Kubota A,Kato H,Yamaguchi H.Unsteady structure measurement of cloud cavitation on a foil section using conditional sampling technique[J].Journal of Fluids Engineering,1989,111(2):204-210.

[2]王波,张永坤,高霄鹏.基于模型试验的螺旋桨空泡噪声计算[J].海军工程大学学报,2010,22(6):87-90. Wang Bo,Zhang Yongkun,Gao Xiaopeng.Calculation of ship propeller cavitation noise based on model experiment[J]. Journal of Naval University of Engineering,2010,22(6):87-90.

[3]刘登成,洪方文,张志荣等.螺旋桨片状空泡的CFD分析[J].舰船科学技术,2009,31(1):43-46. Liu Dengcheng,Hong Fangwen,Zhang Zhirong,et al.The CFD analysis of propeller sheet cavitation[J].Ship Science and Technology,2009,31(1):43-46.

[4]杨琼方,王永生,张志宏等.非均匀进流对螺旋桨空化水动力性能的影响[J].水动力学研究与进展,2011,26(5):538-550. Yang Qiongfang,Wang Yongsheng,Zhang Zhihong,et al.Calculation of highly-skewed propeller’s load noise using BEM numerical acoustics method in frequency domain[J].Acta ArmamentarⅡ,2011,32(9):1118-1125.

[5]胡健,马骋,黄胜等.螺旋桨尾流场的数值计算[J].哈尔滨工程大学学报,2008,29(12):1255-1260. Hu Jian,Ma Cheng,Huang Sheng,et al.Numerical analysis of flow fields behind propellers[J].Journal of Harbin Engineering University,2008,29(12):1255-1260.

[6]Lindau J W,Boger D A,et al.Propeller cavitation breakdown analysis[J].Journal of Fluids Engineering.2005,127:995-1002.

[7]朱德祥,张志荣,吴乘胜等.船舶CFD不确定度分析及ITTC临时规程的初步应用[J].水动力学研究与进展,2007, 22(3):363-370. Zhu Dexiang,Zhang Zhirong,Wu Chengsheng,et al.Uncertainty analysis in ship CFD and the primary application of ITTC procedures[J].Journal of Hydrodynamics,2007,22(3):363-370.

[8]Boswell R J.Design,cavitation performance and openwater performance of a series of research skewed propellers[R].Naval Ship Research and Development Center,Wasington,DC,Report 3339,March 1971.

[9]Kim S E.Multiphase CFD simulation of turbulent cavitating flows in and around marine propuslors[R].David Taylor Model Basin,U.S.A.,June 1982.

Numerical analysis for sheet cavitation noise characteristic of countra-rotating propeller

WANG Shun-jie,WANG Yi-chuan,DAI Wei-guo,LI Bin
(Navy Submarine Academy,Qingdao 266044,China)

In order to study cavitation noise characteristic of contra-rotating propeller,the numerical analysis of counter-rotation propeller cavitation was accomplished by using Schnerr-sauer cavitation model, RNG k-ε turbulence model and dynamic mesh model.The open-water performance was done with DTMB4381 propeller cavitation,the predicted cavity shapes were in agreement with both the experimental observation and numerical simulation result on open literature.And,by calculating and analyzing the contra-rotating propeller cavitation,the sound pressure and power spectrum density of different monitors was solved.The result shows that line-spectrum which is related to the blade frequences of front and rear propeller existing in the power spectrum and the non-uniformity of rear propeller flow is more obviously than front propeller.

sheet cavitation;contra-rotating propeller;numerical analysis

U661

A

10.3969/j.issn.1007-7294.2014.07.006

1007-7294（2014）07-0778-08

2013-12-10

国家自然科学基金资助项目（60901054）

王顺杰（1984-），男，海军潜艇学院博士研究生，E-mail：xiaojie000@163.com；王易川（1976-），男，海军潜艇学院副教授。