金字塔凸壳算法的并行化处理①

张忠武， 王文仲， 桂 丹， 周 宇

(1.佳木斯大学建筑工程学院，黑龙江佳木斯 154007;2.佳木斯肿瘤结核医院，黑龙江佳木斯 15007))

0 引言

凸壳问题是目前实际应用中经常要遇到并且需要加以解决的问题之一，而且更为重的是，凸壳问题是求解当前很多实际问题与理论问题极为重要的工具.所以凸壳问题尤其是平面点集的凸壳计算更加受到学术界的关注.由于平面凸壳所拥有的问题复杂性和实际应用的重要性，平面凸壳算法受到国内外众多专家学的关注，为此做了许多研究工作来研究、改进平面点集的凸壳算法，目的在于提升凸壳算法的执行效率.目前算法比较成熟并广泛被认可的串行凸壳算法有格雷厄姆算法、卷包裹算法，为提高凸壳问题的解决速度，又有一些并行的凸壳算法被提出，其中比较突出的是快速凸壳算法、折半分治算法.笔者多年从事计算几何方面的研究，在总结格雷厄姆算法的基础上，提出了格雷厄姆算法的逆算法，即金字塔凸壳算法.本算法是一种串行算法，因此总体上这种凸壳算法效率还不够高，时间复杂度为O(hn)有进一步提升必要.由于金字塔凸壳算法的自身特点，可以将并行思想引进来改进本算法.为此，本文提出了执行效率更高的基于工作站机群的金字塔凸壳的并行处理方法.

1 平面点的凸壳定义

为论述和书写方便平面离散点集以下用S表示，平面点集S的凸壳由CH(S)表示，平面点集S的凸壳边界将表示为BCH(S).

定义1 在平面坐标系下，将点集S当中x轴值最小的点即为S的最左点，用PL表示.当S中x轴值最小点由多个时取y轴坐标值最小点作为PL;同理，将点集S当中x轴值最大点即为S的最右点，用PR表示.当S中x轴值最大点拥有不只一个取y轴坐标最大的点作为P[1]R

定义2 平面点集S的凸壳表示为CH(S)，若将凸壳CH(S)上结点度数为2的点剔除后，余下的点所构成凸多边形被称之为点集S的子凸壳，用SCH(S)表示[2].

定义3 子凸壳SCH(S)外面的点被称之为子凸壳SCH(S)外点;子凸壳SCH(S)内部的点被称之称为子凸壳SCH(S)内点[2].

定理1 平面点集S中的任意取三点p，q，r，三点坐标分别是(px，py)，(qx，qy)，(rx，ry)，则[3]

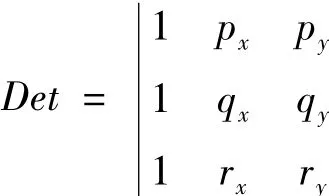
则存在下面点线位置关系

(1)当Det＞0时，点r将位于有向线段p→q的左侧.

(2)当Det＜0时，点r将位于有向线段p→q的右侧.

(3)当 Det=0 时，点 r，p，q共线.

2 金字塔算法的描述与并行算法概述

金字塔凸壳算法是以点集S中最左点PL和最右点PR的有向线段PL→PR为界，把点集S划分为上下两个子集，分别构成相应的子凸壳，再将两者子凸壳合并生成凸壳.具体实施步骤:首先寻找点集 S中的最顶左点PL和最右顶点PR，之后在分别沿着顺时针找出斜率最大点和按逆时针找出斜率最小点，查询确定的这两点必是凸壳顶点，然后再以重复上述步骤逐级寻找其他凸壳顶点，就像搭建金字塔一样一层层构建点集S的二维凸壳边界BCH(S).

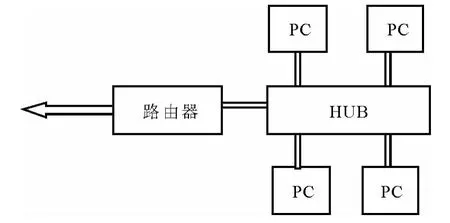
图1 COW系统示意图

并行算法程序实现方法有别于串行算法程序实现方法，并行程序与串行程序的主要区别是串行算法程序实现是通过单线程的方式完成事务变化发展，由于在任何事务之间总存在着某种因果联系，为此应将相关的事务当成一个不可分割的整体.在实际事务的理解和认识上，以往结构化程序实现方法，将一个完整系统视为由众多彼此相互关联的实体构建而成.可是在实现方法仅看到复杂事务表层行为和静态结构关系，不能从事务的深层行为与动态结构关系分解和认识事务.所以从事务实现方式的根本上看，各实体相互之间无法实现并发操作可能，因此也就不存在同时发生相互影响相互作用的并发行为.并行算法程序实现方法的则是将一个纷繁复杂事务行为是由许多个子事务相互作用的结果，子事务之间相互独立可同时运行实现.这造成程序设计实现观念的转变，这种程序设计思想指导的并行算法程序实现方法，核心部分的内容是将复杂事务进行并行划分和算法映射，并行计算模型是其的理论基础.由于并行计算模型决定了程序设计将要采用并行语义，而并行语义将进一步决定程序并行执行的准则，进而确定了并行划分的原则和并行算法程序设计.

3 系统硬件环境

算法实现所用实验的并行计算机是机群系统(COW系统).COW系统拥有编程方便、投资风险小、性价比高、系统结构灵活、能充分将分散在各处的计算机资源，更重要是其具有良好的可扩展性等优点，并且同时COW系统从实际工作条件出发利用当前拥有的网络资源与PC机.COW系统是由客户端与网络构成，从程序实现的角度来说，COW系统是利用面向消息传递程序设计方式，也就是不同的客户端都执行同一个计算机程序，但不同的客户端加载数据有所不同，这样实现程序执行的并行计算.并行计算系统的运行过程示意图见图1，客户端就是实际工作中性能各异的PC机，相互连接的网络是使用以太网技术，其网路数据传输速率为100M/s;实际连接的网络拓扑关系一般使用星型结构，其网络中心是交换机，COW系统的最简配置可由HUB与两台PC机来构成.

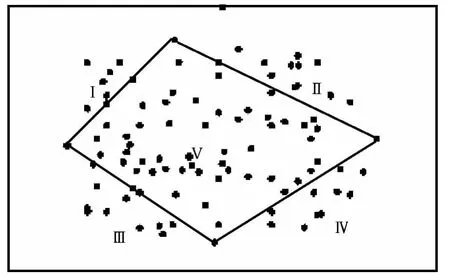
图2 点集区域划分

4 金字塔凸壳算法的并行凸壳新算法

并行算法程序设计的前提条件是将要实现的任务可以在空间与时间上进行分割，达到将不同的计算任务加载到不同终端计算节点上.根据上述对金字塔算法的描述可对平面点集进行划分生成不同的子集，其中子集V所含的点集必定不在凸壳边界上，可先将其中的点删除出去，这样可极大提升算法的执行效率.在图2所示的点集中，子集Ⅰ，Ⅱ，Ⅲ，Ⅳ，Ⅴ都是在自己范围内寻找最左和最右点，可是在这个执行过程中每个子集间没有产生数据交叉，各子集间可同时在不同的终端上运行.因此可将所有点集先在主机中进行分割，划分成不同点子集，不同子集分别使用同步设置通过网络消息传递在同一时间步上发送数据到并行的各个终端计算节点，各终端节点独立查询最左和最右凸壳顶点，各节点定点查询完毕后再各自发送给主机进行汇总处理.通过采用数据划分进行并行计算极好的解决海量数据在串行计算实现中时间效率差的难题.下面是在COW系统上实现金字塔凸壳算法的并行算法步骤:

步骤1:在主机上预先用初始近似凸壳算法对平面点集进行区域划分处理，寻找点集中上下左右四个方向的极值点，将点集划分为五个子点集，剔除明显不能构成凸壳边界的子集V所含点，组件4个并行处理机群.

步骤2:通过并行化处理分别在子机群COWi(1＜i＜4)上对各子集域Si中点进行查询构建各自子凸壳边界顶点.

步骤2－1:在子集Si上用子机群COWi寻找斜率极值点，确定子凸壳边界顶点Qi的并行处理.

步骤2－2:删除左新顶点Qi，L，和右新顶点Qi，r所连成的直线下方的所有点的并行处理.

步骤2－3:对寻找到的子凸壳Qi的所有顶点进行标记处理.

步骤3:凸壳边界的生成.依次将划分的各子集所查询确定的顶点，相互连接构建生成二维点集的凸壳Q.

5 结束语

本文提出的金字塔凸壳算法的并行处理方法，在时间和空间复杂度上不但好于传统的串行算法(格雷厄姆凸壳算法、卷包裹凸壳算法)和并行算法(折半分治凸壳算法)，同时拥有较好的扩展性，可推广到更多机群上实现凸壳并行处理.在当下信息化的背景下，GIS系统得到广泛应用，GIS所处理的数据多为海量数据点，如何快速处理海量数据倍受关注.本文提出的金字塔算法的并行处理正是对这方的一种尝试，取得了很好的执行效果.

[1]金文华，何涛，唐卫清等.简单快速的平面散乱点集凸壳算法[J].北京航天航空大学学报，1999，25(1):73－76.

[2]王杰臣.2维空间数据最小凸包生成算法优化[J].测绘学报，2002，31(1):82－86.

[3]张忠武，吴信才.平面海量散乱点集凸壳算法[J].计算机工程，2009，35(9):43－45，48.