锈后预应力混凝土梁整体性能研究①

谷云秋， 叶文亚， 周雪峰， 彭 卫

(1.宁波市公路管理局，淅江 宁波 315040;2.余姚市公路管理段，浙江 余姚 315400;3.浙江大学宁波理工学院，浙江 宁波 315000)

0 引言

关于结构性能退化方面的研究，最常用的方法是对影响截面承载力的因素进行统计分析[1]，并依照工程经验找到各因素的分布规律[2]，进行截面承载力的敏感性分析，这种分析对于构件来说是合理的[3～4]，但对于结构来说，由于局部退化的速率不同而导致相邻截面的应力重分布是无法考虑的.由于钢筋锈蚀膨胀对周围混凝土应力场的影响，导致混凝土胀裂，截面有效高度改变和钢筋本身截面的损失是截面承载能力下降的主要因素.从结构的角度出发，考虑结构型式的各异和结构构件各截面损伤程度的差别，计算结构的整体性能.

1 分析模型及参数

为了掌握钢筋截面损失和混凝土剥落对超静定结构整体性能的影响，采用实体建模，如采用实桥建模，单元太多，计算时间过长，故选择一3跨试验梁做研究对象.

本文选用文献[5]模型梁，具体参数为:(1)跨径组合:3.1m+3.6m+3.1m，边跨/中跨 =0.86;(2)通长预应力钢筋采用6Φ5钢丝，由Φj15.24钢绞线(7根Φ5的钢丝)抽掉中间一根得到，在粘贴应变片处仍然填入，以保证测得的钢绞线应变的准确性，墩顶短束采用3Φ5钢丝，由同样Φj15.24钢绞线抽掉其中4根得到，试验性能良好;(3)为了对墩顶短束进行锚固，在中支座左右两侧分别设置了锚固块，其内配置防崩钢筋;(4)考虑到墩顶短束张拉不方便，预应力钢丝均采用单端张拉，张拉控制应力均为1395MPa.取半桥有限元网格划分模型的进行分析.

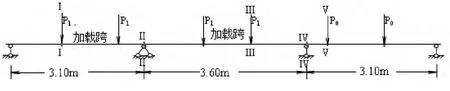
图1 预应力混凝土梁计算模型的尺寸

表1 试验梁参数

图1为荷载作用点位置，P1为作用外载，P0为 荷载补偿时所加力.试验梁参数如表1.

2 退化方式的选择

假定(1)认为钢筋沿长是均匀锈蚀的，钢筋锈蚀对应钢筋面积的减少，没有考虑因为钢筋锈蚀导致钢筋屈服强度的变化;(2)认为钢筋的锈蚀面积的缺损相应得会导致混凝土表层的剥落.(3)普通钢筋锈胀导致混凝土剥落，预应力钢筋锈蚀大都是应力锈蚀引起的，因此只考虑锈蚀后截面面积的减少，而不考虑锈胀对周围混凝土的作用.

钢筋面积的减少率和混凝土剥落量之间的关系还有待大量的统计资料的验证，根据文献[6]统计分析和有限元模拟局部锈胀引起周围应力场分布的研究，拟选择如表2方式退化.

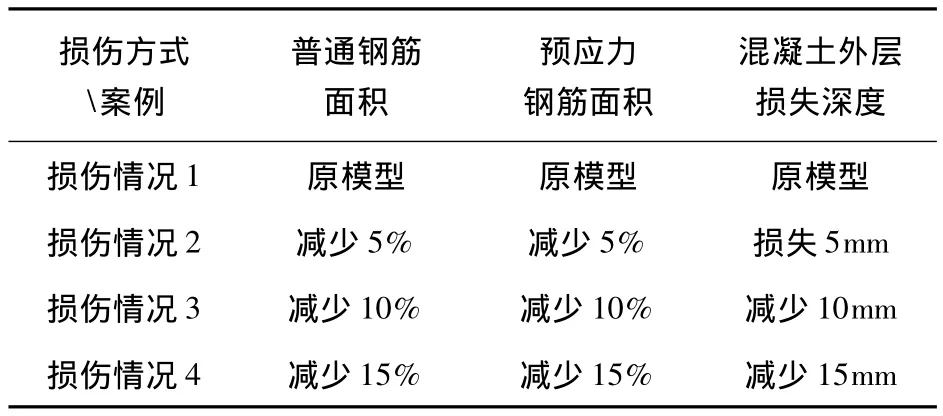
表2 损伤方式的选择

为了表达清晰起见，以下计算成果图中将损伤情况1称为原模型，损伤情况2称为退化5%，损伤情况3称为退化10%，损伤情况3称为退化15%.

3 极限承载力参数敏感性分析

3.1 混凝土性能分析

分析了预应力混凝土连续梁各跨跨中上下缘混凝土主压应力和预应力混凝土连续梁各跨跨中上下缘混凝土主拉应力.如图2～3.

图2 荷载－混凝土应力曲线

分析混凝土上下缘是应力曲线可以看出，混凝土主压应力呈现随外荷载的逐渐增大而增大的规律，而相同位置处的主拉应力随荷载的时程曲线呈现复杂的趋势，原模型在左跨跨中有1.25MPa左右的初始主拉应力，中跨跨中无论那种情况，都是初始主拉应力为零，在裂缝发生前，主拉应力随着外荷载的增加而增加，但裂缝一旦发生，周围混凝土应力场发生应力重分布，而后，继续随着外荷载的增加，混凝土主拉应力呈上升趋势，原模型的主拉应力在极限承载力下达到最大，左跨跨中位置处接近3MPa.

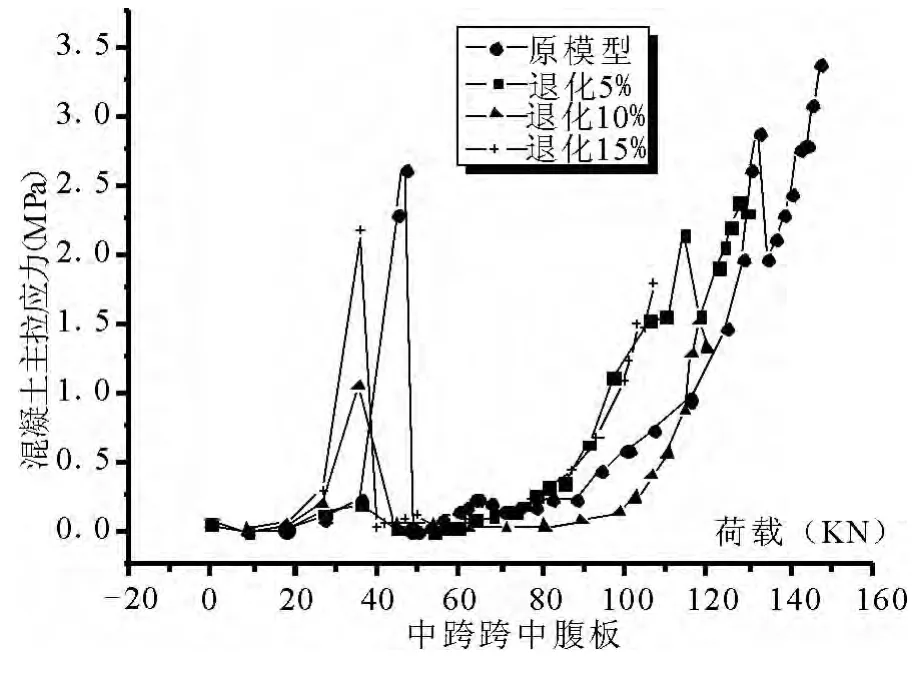
图3 荷载－混凝土应力曲线

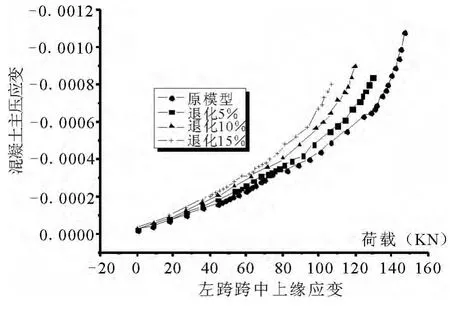
图4 荷载－混凝土应变曲线

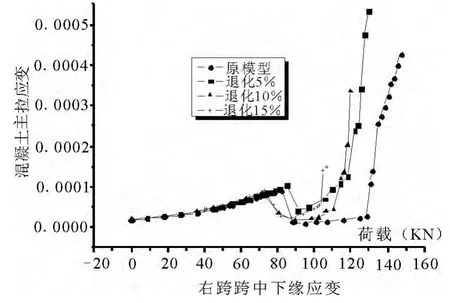
图5 荷载－混凝土应变曲线

分析腹板的荷载－应力曲线，得到腹板处裂缝出现时的外载大于40kN，说明腹板处裂缝出现时间比底板处的混凝土晚.原模型出现主拉应力达到极限强度的外荷载最大，退化越多，极限荷载越小.腹板处主拉应力出现第2个峰值时，表明该处普通钢筋进入屈服，混凝土再次应力重分布.从荷载－应力时程曲线可是清楚得看出混凝土加载过程中的性能演变过程.

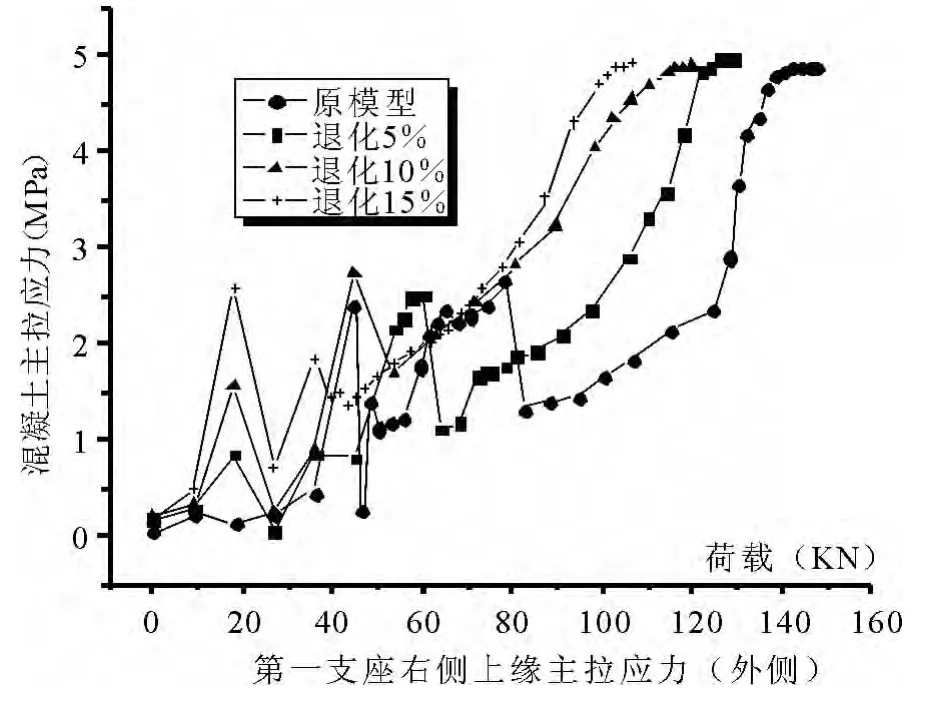
图6 荷载－混凝土主拉应力曲线

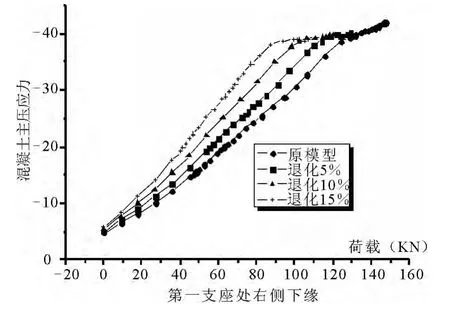
图7 荷载－混凝土主压应力曲线

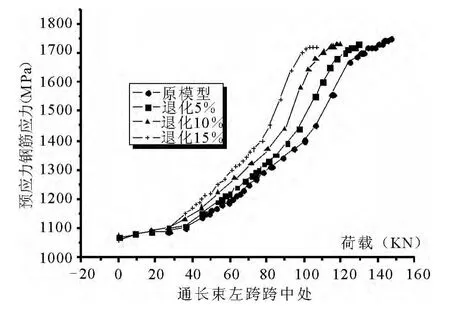
图8 荷载－预应力筋应力值曲线

分析了预应力混凝土连续梁各跨跨中上下缘混凝土主压应变和预应力混凝土连续梁各跨跨中上下缘混凝土主拉应变，如图4～5.

右跨跨中下缘有初始压应变，表明在施工阶段结束后，混凝土梁下缘是受压的，随着在左跨和中跨继续增加外荷载时，右跨下缘混凝土主压应力继续增加.右跨跨中上缘混凝土主拉应力在混凝土开裂前是随外载的增加而增加的，发生开裂后，发生应力重分布，当总体趋势是增大的.

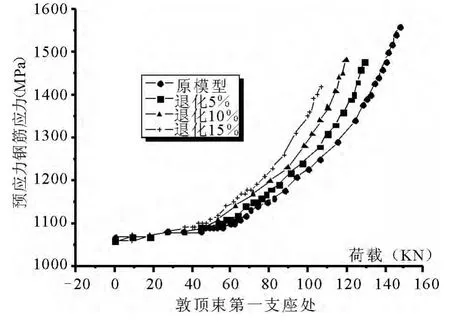
图9 荷载－预应力筋应力值曲线

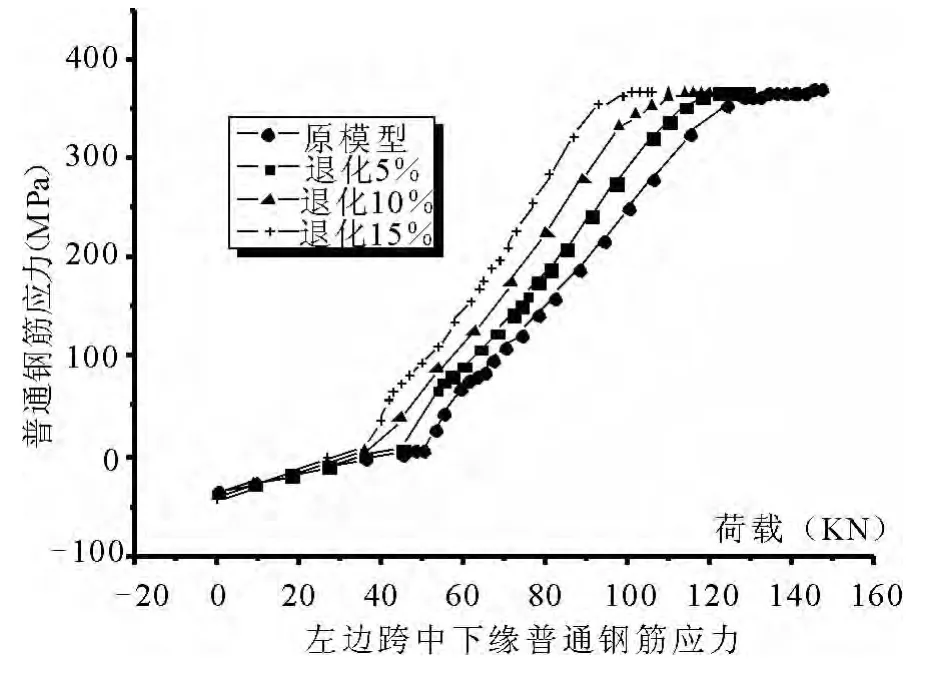
图10 荷载－普通钢筋应力时程曲线

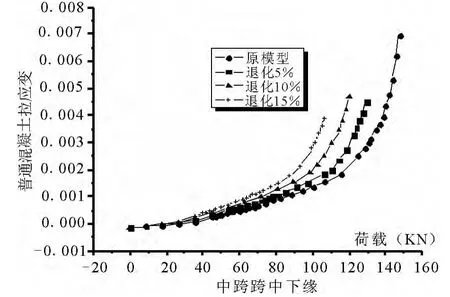
图11 荷载－普通钢筋应力时程曲线

分析了位于支座处的混凝土的应力图，如图6～7.可以看出支座处上缘混凝土裂缝发展较早，经过应力重分布的调整，总的趋势是随外荷载的增加主拉应力增加，最后达到极限抗拉强度.支座处下缘混凝土主压应力在无退化情况下，相同情况下，达到极限抗压强度时的外荷载最大，依据退化程度的增大，达到抗压强度极限的外载相应降低.表明该连续梁是从右侧上缘压溃的.左跨跨中腹板中轴线处的主拉应力不大，均在正常范围.腹板处主压应力不算大，时间历程中没有达到设计极限抗压强度.

3.2 预应力性能分析

分析了通长束位于左跨跨中、左跨1/4、中跨跨中及敦顶束在第一支座处的荷载－预应力应力值曲线.预应力筋在不同部位的应力分布如图8～9.通长束在左跨跨中处达到极限强度，可以看到当混凝土未开裂时，预应力钢筋的应力值是相同的，当裂缝出现后，梁体刚度出现变化，当外载继续增加时，从图中可以看出曲线曲率的突变，梁体刚度继续减少，最后达到屈服.

可以看出通长束只有在左跨跨中达到屈服，其他位置都没有达到屈服，但在极限外载下，左跨跨中预应力钢束的应力达到了1600～1700MPa;左跨1/4处预应力钢束的应力达1400～1500MPa;敦顶处的预应力钢束的应力为1400～1600MPa;没有达到屈服的预应力钢筋在没有退化的情况下，达到的应力最大.从某种意义上来说，材料利用得更合理、更充分.通长束右跨跨中处(无太大变化)，右跨1/4处有很大的增长，但没有达到屈服强度.

3.3 普通钢筋性能分析

分析了预应力混凝土连续梁左跨跨中下缘、中跨跨中下缘普通钢筋的应力和应变时间历程变化.看到左跨跨中和中跨跨中的普通钢筋在极限承载力作用下均已经达到屈服，只是屈服时的荷载值不同.退化越多，越早出现屈服.如图10～11.

归纳荷载－钢筋应力应变曲线图、原模型及各种退化模型混凝土裂缝荷载和钢筋屈服荷载，左跨跨中裂缝开始出现的荷载分别为原模型50.12kN、44.75kN、35.8kN、35.8kN.而中跨开始出现裂缝的荷载都是35.8kN.在同一荷载作用下，退化越多，普通钢筋应力应变越大，最后都达到屈服.

4 结论

耐久性损伤对寿命期预应力混凝土连续梁的极限承载能力有重要影响，计算结果表明，随着损伤的加大，极限承载力下降，根据梁中控制截面处混凝土、普通钢筋及预应力的荷载－应力应变曲线可以清楚地看出，相同的外载作用下相应位置处的寿命期应力应变演变过程.本文考虑纵向均匀损伤的情况下，退化前后，极限承载力破坏位置基本不变.因此为了更好地了解预应力混凝土桥梁的性能退化规律，有必要在施工初期预埋耐久性检测或监测设备，可以获取即时或定时的耐久性损伤数据，为确定该桥的整体性能提供定量的数据.准确得计算服役期桥梁的力学性能.根据监测到的耐久性数据，可以归纳总结出材料的退化规律，进而指导桥梁全寿命设计.

[1]Aruz Petcherdchoo，Maintaining Condition and Safety of Deteriorating Bridges by Probabilistic Models and Optimization，University of Colorado，Department of Civil，Environmental and Architectural Engineering，2004.3.

[2]Frangopol，D.M.，Kong，J.S.，and Gharaibeh，.E.S.，Reliability－ based Life－cycle Management of Highway Bridges，Journal of Computing in Civil Engineering，ASCE，2001，15(1):27－34.

[3]M.Dekoster，F.Buyle－Bodin，O.Maurel.Modeling of the Flexural Behaviour of RC Beams Subjected to Localised and Uniform Corrosion Engineering Structures，2003，Vol.25(10):1333－1341.

[4]Roberto Capozucca，M.Nilde Cerri.Influence of Reinforcement Corrosion－in the Compressive Zone－on the Behaviour of RC Beams Engineering Structures，2003，Vol.25(13):1575－1583.

[5]冷金荣.预应力混凝土连续梁抗弯承载力试验研究[D].上海:同济大学，2006.3.

[6]叶文亚.预应力混凝土桥梁全寿命整体性能研究[D].上海:同济大学，2007.9.