对角切片高阶累积量干扰检测技术研究

范广伟，路瑜亮，晁 磊

(1.河北省卫星导航技术与装备工程技术研究中心，河北石家庄050081;2.总装北京军代局驻石家庄地区军代室，河北石家庄050081)

0 引言

由于GNSS系统导航信号较为微弱，即使微弱的干扰也有可能对GNSS接收机的精度和稳定性造成影响，因此有必要对卫星导航频段内的干扰信号进行检测，确定是否有干扰信号对卫星导航系统造成影响，排除干扰对卫星导航系统的影响。

卫星导航系统的干扰检测由于不知道信号的类型、相位和幅度等特征，检测起来难度相对较高。能量检测［1－3］是最常见的频谱感知方法，无需知道信号先验知识，计算一段时间内接收到的信号能量并与事先设置的门限值进行比较，从而判断有无信号存在;计算复杂度低，实现也相对简单，因此比较适于引入到缺乏先验知识的干扰检测［4］当中。然而这种检测方法弱点是受未知噪声影响严重，将直接导致检测性能下降，甚至检测结果不可信。高阶统计量方法因其对多种噪声都有很好的抑制作用逐渐成为信号处理的新热点，是近年来发展较快的现代信号处理方法之一［5，6］，Nikias［7］最早提出可以利用信号高阶累积量进行信号检测。由于高斯过程的三阶及以上累积量为零［8］，使得高阶累积量在高斯色噪声处理中具有先天的优势，因此基于高阶累积量的方法在处理受高斯噪声污染的过程时，能够极大地提高干噪比。

对此提出了基于高阶累积量对角切片的干扰信号能量检测算法，并与时域及频域的能量检测算法进行了对比，采用了递推算法获得高阶累积量对角切片，减小了计算量。通过仿真验证了算法的有效性。

1 能量检测

信号的能量检测法是一种有效的信号检测方法，早在1967年 H.Urkowitz研究了未知确定信号的能量检测算法［9］。所谓能量检测法是指计算信号在特定时间内的能量，与预先设定的门限值进行比较，做出判决，获得检测结果。

1.1 时域能量检测

能量检测器模型如图1所示，由带通滤波器、数模转换器件、平方律器件和比较判决器组成。为了有效测量接收信号的能量，将接收信号x(t)先经带通滤波器滤波，再经过一个数模转换器，把模拟信号离散化，然后进行平方求和，最后经过判决器与判决门限λ比较做出判决。

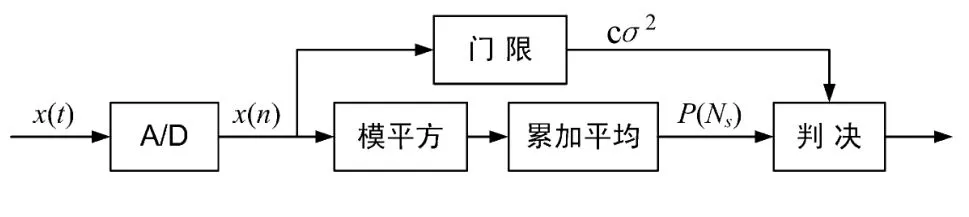
图1 时域能量检测原理

图1中，Ns与检测时间有关，Ns越大，能量检测精度越高，但检测时间也越长。判决门限为cσ2，c为常数因子，σ2为接收输入端的噪声功率。

经过采样后，信号检测面临的是这样一个假设检验的问题，即

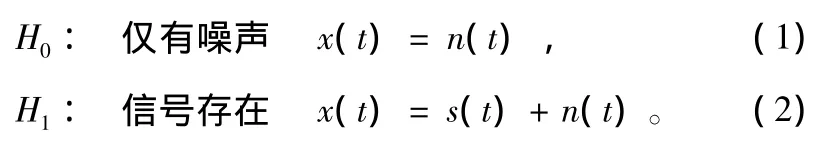
若噪声和干扰信号为高斯分布的平稳随机过程，则要处理的信号模型为高斯噪声背景下高斯信号的最佳检测问题。将接收信号x(t)离散表示为x1，x2，…，xn，根据奈曼—皮尔逊准则在虚警概率小于某一事先给定值的情况下，使检测概率最大，可以推导出在这种情况下的最佳检测器为:

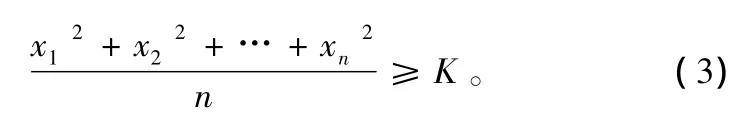
这种检测器称为能量检测器，把输入的n个样本值平方之后再求平均，然后与某一阈值比较。这个系统的增益为GT=5(lgT－lgτ^)，T为积分时间，τ^为噪声等效相关半径。从理论上说，积分时间越长，系统的时间增益就越大，但增益的提高并不是没有限制的，因为当观测时间太长时，噪声的平稳性就无法保证了，在应用中要根据情况决定积分时间。

1.2 频域能量检测

能量检测算法也可在频域上实现，具体实现与谱分析仪类似，如图2所示。

图2 频域能量检测原理

FFT运算后，可以在若干频点上进行平均，以获得系统感兴趣的频率范围内的干扰功率P( Ns)，频域的能量检测算法常应用于检测具体的干扰频点位置。时域和频域上的计算是完全等效的。

1.3 性能仿真

下面对时域和频域能量检测算法的性能进行仿真，取常见的BPSK、ASK、MSK、单频信号和线性调频信号作为常见的干扰信号类型进行对比仿真，仿真结果如图3和图4所示。

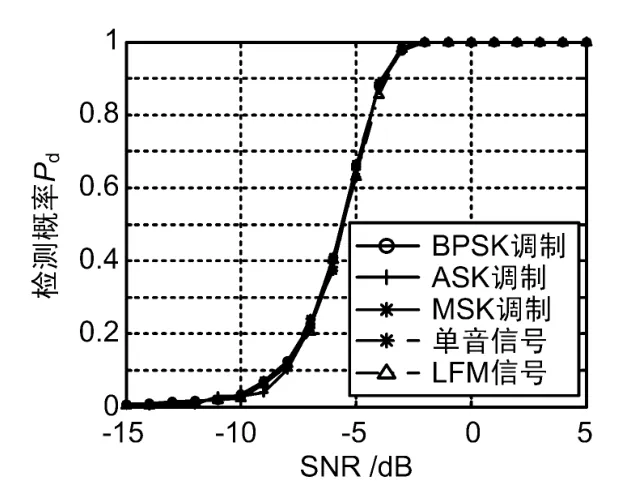
图3 时域能量检测

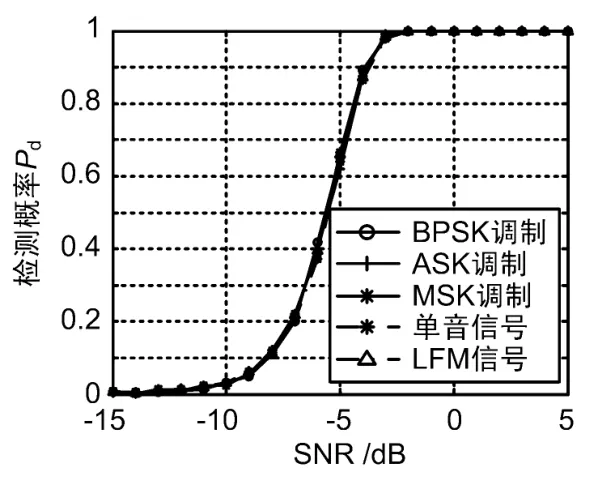
图4 频域能量检测

图3为不同调制方式信号的时域能量检测算法，图4为不同调制方式信号的频域能量检测算法，采样点数都是1 000个数据点、虚警概率都是0.001条件下的检测概率随信噪比变化的曲线。从图3和图4中可以看出:时域能量检测算法和频域能量检测算法的检测性能大体相同，并且能量检测算法的检测性能和信号的调制方式基本无关;但是基于时域的干扰检测只能够判定一个频段中是否存在干扰，并不能准确地判定具体干扰频点位置，而频域上的能量检测可以在检测干扰的同时判断出干扰频段的确切位置。缺点是外界未知的干扰和噪声非常敏感，即使自适应的设置检测门限，任何带内干扰都有可能造成检测结果的偏差，并且对微弱信号的检测性能较差。

2 三阶对角切片累积量检测

由于高斯噪声的三阶及三阶以上的累积量为零，所以高阶累积量对高斯过程不敏感，能有效地抑制高斯噪声，可从高斯过程中检测出非高斯信号。因此将高阶统计量应用到卫星导航干扰检测中可获得好的性能。

2.1 高阶累积量定义

k阶平稳过程x()t的k阶累积量定义为:

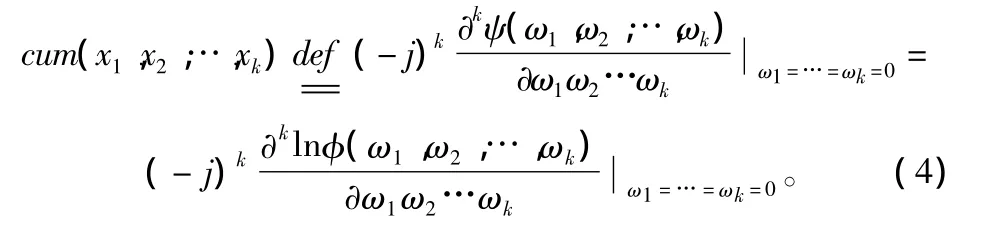
通常把最常见的k阶矩和k阶累积量分别记为:

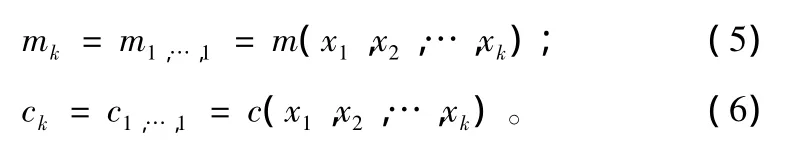
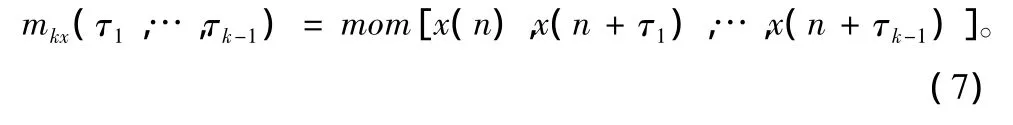
而 k 阶累积量 ckx(τ1，…，τk－1)定义为:

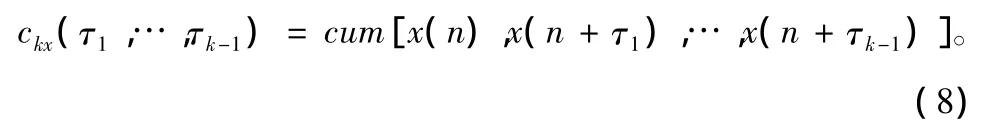
比较上式可知，平稳随机过程 x(n{ })的k阶矩和k阶累积量实质就是取x1=x(n)，x2=x(n+τ1)，…，xk=x(n+τk－1)之后的随机向量的 k阶矩和k阶累积量。由于 x(n{ })是k阶平稳的，故其k阶矩和k阶累积量均只有k－1个独立的变元。它们仅仅是滞后 τ1，…，τk－1的函数，而与时间 n无关。

2.2 递推对角切片的三阶累积量

对于零均值的平稳随机过程，其三阶累积量可由M-C公式直接得到。对于零均值的局部平稳随机过程x(n)，其二阶累积量为:

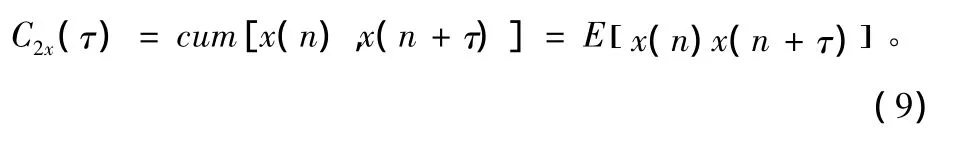
三阶累积量为:

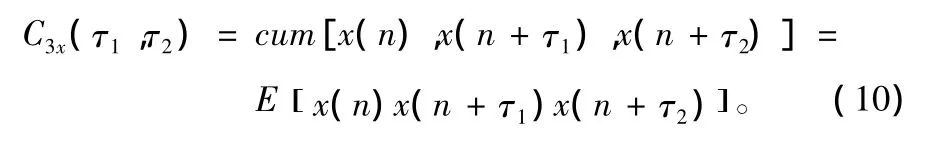
三阶累积量对角切片为:

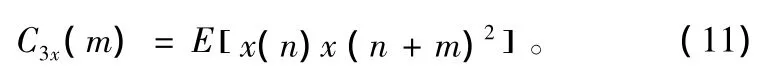
在计算高阶累积量时使用递推的方法，可以结合更多数据进行计算而不会加大计算量，并节省了存储空间，便于实时处理数据。

二阶累积量递推估计公式为:

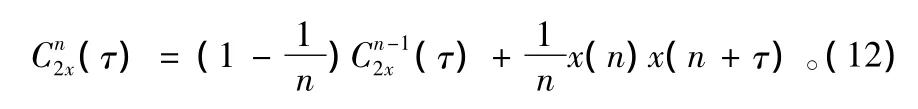
三阶累积量递推估计公式为:

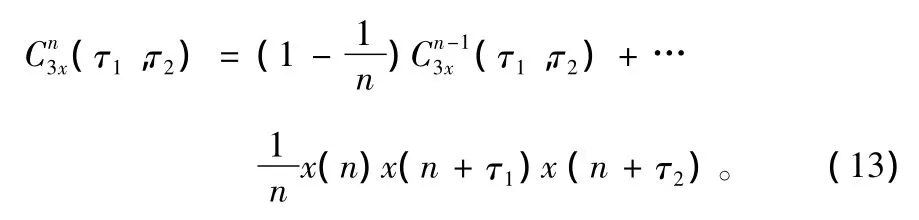
理论上高斯噪声的高阶累积量为零，因此可以使用高阶累积量检测高斯噪声背景下的非高斯信号，但由于需要足够的数据而导致计算量庞大而无法实时处理。高阶累积量对角切片包含了干扰概率分布的非高斯性信息，而高斯噪声的对角切片为零，因此仅计算对角切片，在抑制高斯噪声的同时可极大地减小运算量。采用递推高阶累积量对角切片在实时处理数据时可以将更多数据结合起来进行计算，使计算结果更加精确，逼近其统计特性。

对干扰数据进行检测，得到三阶累积量对角切片C3x(m)，其模平方和的平均为:

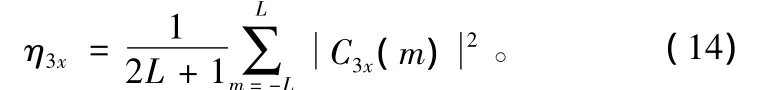
为检验统计量，L为采样点最大延迟，将检验统计量与门限比较得出判决结果，检测模型如图5所示。

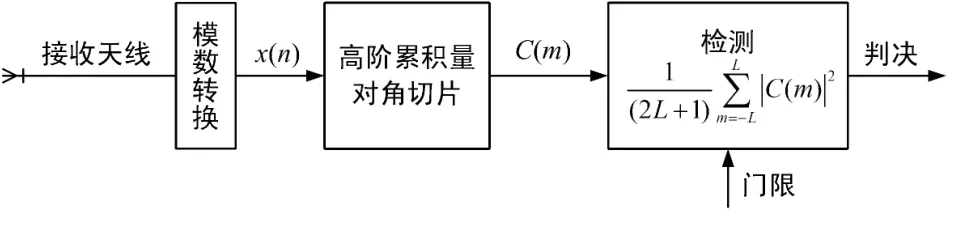
图5 三阶对角切片检测模型

2.3 性能仿真

下面仿真验证本文提出算法的检测性能，同样取上面几种信号进行对比仿真，仿真结果如图6所示。

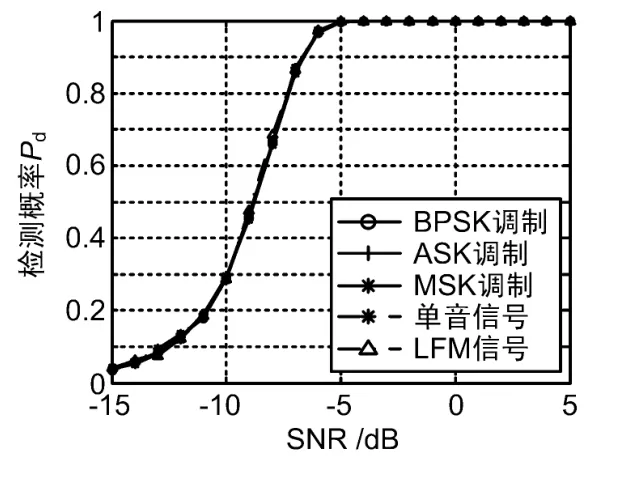
图6 三阶对角切片检测

图6为不同调制方式信号的递推三阶对角切片能量检测算法，在采样点数1 000个数据点、采样点最大延迟为100、虚警概率都是0.001条件下的检测概率随干噪比变化的曲线。从图中可以看出，该算法对干扰的类型不敏感，对不同的干扰类型均具有较好的检测概率。

3 性能比较

下面分别仿真在高斯白噪声信道下基于递推对角切片的能量检测算法的性能。信噪比从－15 dB变化到5 dB，采用零中频的线性调频信号作为干扰信号，带宽为20 MHz，采样频率46 MHz，与时域及频域能量检测算法进行对比，蒙特卡洛仿真试验的次数取1 000次。

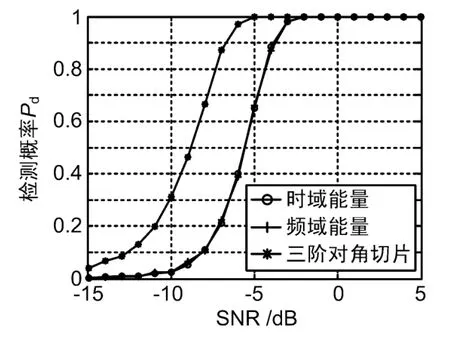
图7 检测性能对比

时域、频域和三阶对角切片累积量算法在不同干噪比下的检测性能曲线如图7所示。从图7中可以看出，时域和频域能量检测算法性能近似，在0.001的虚警概率下，干噪比为 －2 dB时能达到100%检测概率，而基于递推的三阶对角切片的累积量算法在－5 dB时就能达到100%检测概率，说明本文算法有更好的微弱信号检测性能。

4 结束语

在高斯白噪声的环境下，利用三阶累积量切片对高斯噪声的自然盲性和对高斯色噪声的良好抑制性能，给出了一种递推的对角切片的高阶累积量的能量检测算法，在高斯背景噪声下能有效地检测到各种微弱的干扰，相比时域和频域的能量检测算法，具有抗噪性能好和检测门限低等特点，具有良好的工程应用前景。

［1］KOSTYLEVV.Energy Detection of a Signal with Random Amplitude［J］.IEEE Int.Conf.Commun.，2002，3(4):1 606－1 610.

［2］WU J B，LUO T，YUE G X.An Energy Detection Algorithm Based on Double-Threshold in Cognitive Radio Systems［C］∥2009 1stInternational Conference.Information Science and Engineering.Nanjing，CN:IEEE Press，2009:493－496.

［3］ANDREA MARIANI，ANDREA GIORGETTI，MARCO CHIANI.Effects of Noise Power Estimation on Energy Detection for Cognitive Radio Applications［J］.IEEE Transactions on Wireless Communications，2011，12(12):3 410－3 420.

［4］薛 峰，张 军.GPS接收机自主干扰检测方法研究［J］.无线电工程，2009，39(7):14 －16.

［5］HINICH M J.Detecting a Transient Signal by Bispectral Analysis Acoustics，Speech，and Signal Processing［J］.IEEE Transactions on，1990，38(7):1 277 －1 283.

［6］HINICHM J，WILSON G R.Detection of Non-Gaussian Signals in Non-Gaussian Noise Using the Bispectrum［J］.IEEE Transactions on，1990，38(7):1 126 －1 131.

［7］CHRYSOSTOMOS L N，JERRY M.Tutorial on Higerorder Statistics(spectra)in Signal Processing and System Theory［J］.Theoretical Results and Some Applications.IEEE Proc.，1991，3(79):278 －305.

［8］张贤达.时间序列分析——高阶统计量方法［J］.北京:清华大学出版社，1996.

［9］URKOW ITZ H.Energy Detection of Unknown Deterministic Signals［J］.Proc IEEE，1967，55(4):523－531.