自复位钢筋混凝土框架振动台试验的数值模拟

高文俊吕西林

（同济大学结构工程与防灾研究所，上海200092）

自复位钢筋混凝土框架振动台试验的数值模拟

高文俊*吕西林

（同济大学结构工程与防灾研究所，上海200092）

为了对自复位钢筋混凝土框架结构的抗震性能进行研究，同济大学土木工程防灾国家重点实验室根据相似关系设计与制作了一大比例自复位钢筋混凝土框架，并进行了模拟地震振动台试验。振动台试验模型为单跨两层两榀框架，采用了自复位形式的柱脚节点与梁柱节点，由后张拉无黏结预应力筋提供恢复力。试验选取了El Centro波和汶川波作为单向（X方向）激励输入，研究了结构在多遇地震、基本地震和罕遇地震下的抗震性能。本文主要采用OpenSEES有限元软件对试验模型框架进行数值模拟，并对梁柱节点与柱脚节点提出有效的模拟方法。此外，对该框架进行弹塑性时程分析并与试验实测结果进行对比，对比结果表明本文所提的数值模拟方案能较好地反映试验模型结构的振动特性。

自复位钢筋混凝土框架，数值模拟，OpenSEES，振动台试验

1 引 言

自复位钢筋混凝土框架结构是一种新型抗震结构，它与传统的钢筋混凝土框架的区别［1］在于：①放松了柱脚与基础之间的约束，使得上部结构与基础交界面之间可以传递压力，但不能传递拉力，并且在水平倾覆力矩的作用下，允许上部结构在基础交界面处发生一定的抬升；②放松了构件间的约束，允许框架梁的转动使结构发生摇摆；③在梁柱构件中设置后张拉无黏结预应力筋，预应力筋在结构发生摇摆的过程中提供恢复力，在震后使结构回复到原有位置，从而减小结构的残余变形。

自复位的概念来源于对预制无黏结预应力混凝土框架的研究。Cheok等［2］和Priestley等［3］先后对设置有无黏结预应力筋的混凝土梁柱节点进行了试验研究，El-Sheikh等［4］对设有无黏结预应力筋的混凝土框架进行抗震分析，分析结果表明这类框架的力学性能在设计地震（DBE）下呈非线性弹性，而且结构几乎没有受到损坏，即使在大震（MCE）的作用下，也不会发生倒塌，结构具有良好的抗震性能。刘兢兢等［5］设计制作了一大比例自复位钢筋混凝土框架，并进行了模拟地震振动台试验。首先，本文将对该缩尺框架进行简要的回顾；然后重点分析自复位节点在水平侧向力作用下的特点；最后，采用OpenSEES有限元软件对试验框架结构进行了非线性仿真模拟。

2 试验概况

2.1 试验模型概况

如图1所示，模型结构为单跨两层两榀框架，平面尺寸为3.0 m×1.5 m。X向（振动方向）框架梁内设有无黏结预应力筋，梁柱节点处增设有顶底角钢连接构造；Y向框架梁与柱固接。每层框架的层高均为1.5 m，在层高处不设楼板，在每一层放置4.8吨的质量块。试验模型制作采用细石混凝土分两次浇筑并预留标准试块：一层混凝土立方体抗压强度试验值为42.4 MPa（试块尺寸150 mm× 150 mm×150mm），弹性模量3.24×104MPa（试块尺寸100 mm×100 mm×300 mm）；二层混凝土立方体抗压强度试验值为54.4 MPa，弹性模量4.13 ×104MPa。框架梁柱构件配筋见图2。

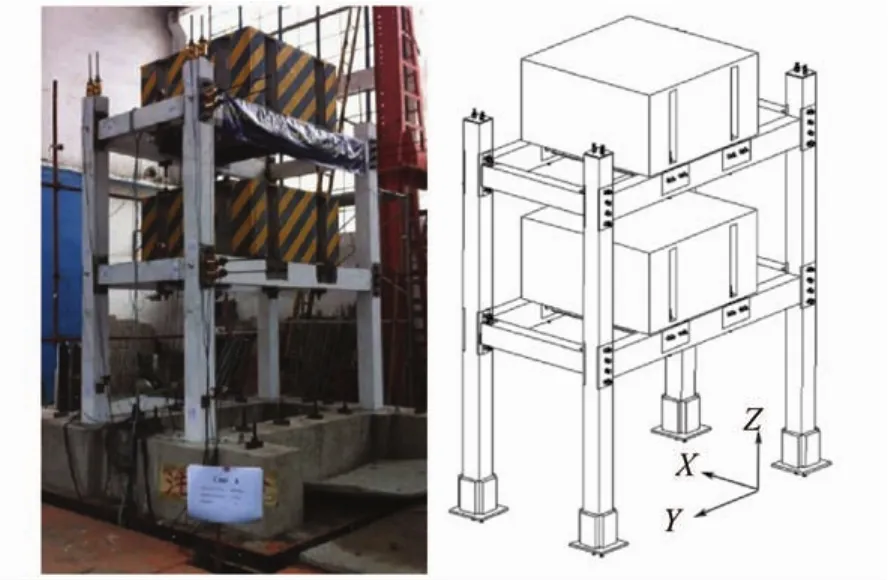
图1 试验结构模型Fig.1 The structuralmodel of the test

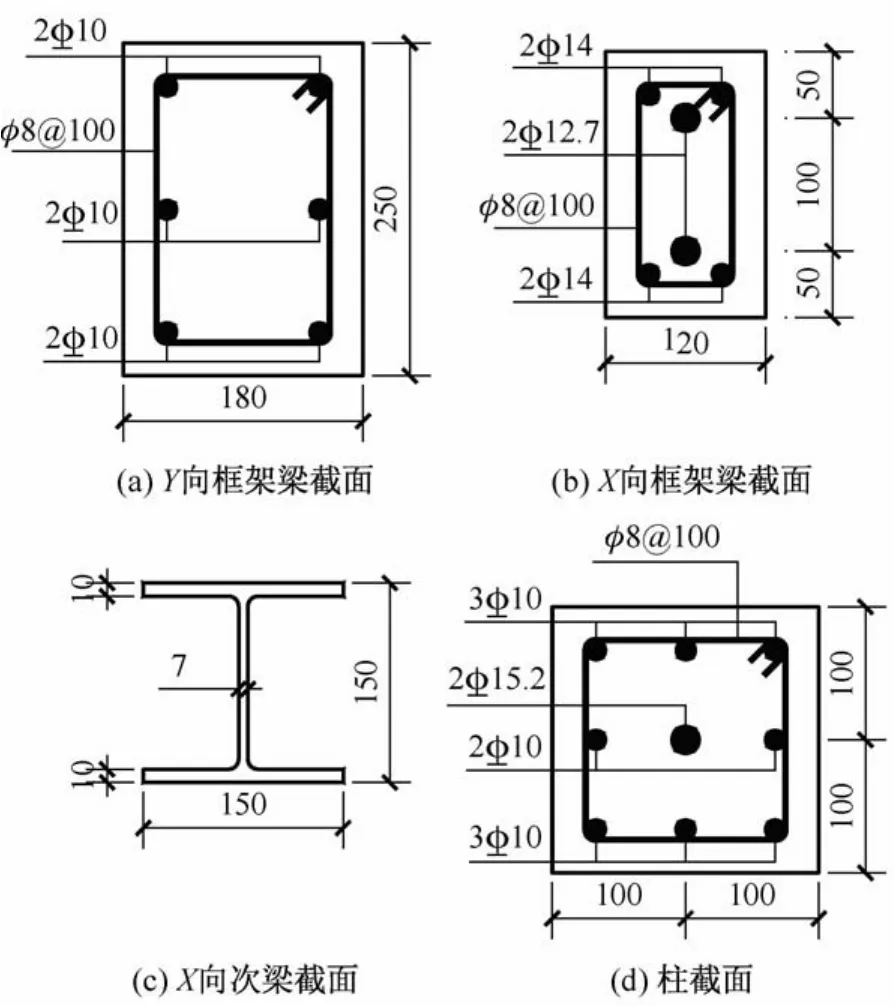
图2 框架梁柱构件配筋Fig.2 Reinforcement of specimens

2.2 自复位柱脚节点

柱脚节点如图3所示，柱内张拉有无黏结预应力筋柱插入基础300 mm，柱内的预应力筋分别锚于柱顶和埋置于基础中的钢板。柱底嵌有20 mm厚钢板。基础杯口与柱身之间50 mm的间隙，间隙内放置橡胶块。橡胶块厚度为50 mm，国际硬度为60，弹性模量为4.45 N／mm2。柱内的预应力筋是两束钢绞线，每束的公称直径为15.2 mm，截面面积为140 mm2，屈服强度fy＝1 581 N／mm2，极限强度fu＝1 860 N／mm2，弹性模量为1.95×105MPa。柱中非预应力筋焊于柱底的钢板，不与基础接触，钢筋型号为HRB335，屈服强度为335 MPa，弹性模量为2.0×105MPa。

图3 自复位柱脚节点Fig.3 Self-centering column-base joint

2.3 自复位柱梁节点

自复位梁柱节点构造如图4所示，梁中的无黏结预应力钢筋锚于框架柱的外侧。梁内的预应力筋采用的是钢绞线，共两束，每束的公称直径是12.7 mm，截面面积为98.7 mm2，屈服强度fy＝1 673.7 N／mm2，极限强度fu＝1 860 N／mm2，弹性模量为1.95×105MPa。梁内纵向非预应力钢筋的型号为HRB335，屈服强度为335 MPa，弹性模量为2.0×105MPa。梁端与柱身两侧均设有厚度为20 mm的钢板。梁端还设有顶底角钢与柱连接，角钢的钢材为Q235，屈服强度为235 MPa。

图4 自复位柱梁节点Fig.4 Self-centering beam-column joint

3 有限元数值模型

本文选用OpenSEES［6］有限元软件进行数值模拟，梁柱构件采用的是基于力法的纤维单元。模拟的难点在于反映结构振动过程中自复位梁柱节点的打开（opening），以及结构在摇摆过程中柱脚的抬升（uplift）。

3.1 自复位柱脚节点数值模型

如图5所示，柱脚的变形模式由两部分构成：①柱身绕柱底截面转动中心的转动；②悬臂柱的弯曲。在柱脚抬升出现前，由于预应力筋的张拉，柱底截面上的纤维均受压。此时柱的受力性能与普通固接的悬臂柱没有任何区别。随着水平荷载的不断增加，柱底钢板与基础钢板之间将出现抬升的临界状态，称为消压状态［4］（decompression limit state），即由竖向力和预应力引起的截面边缘混凝土的压应力首次被由倾覆弯矩引起的拉应力抵消。柱脚抬升的出现表明节点刚度开始进入非线性阶段。随着柱脚的逐渐抬升，柱底截面转动中心开始从柱底截面的中部逐渐向柱最外层纤维靠近，同时柱底与基础之间的接触面积逐渐减小。目前，利用纤维模型模拟构件端部打开的模拟方式主要有两种［7］：①Kurama建议忽略柱内非预应力钢筋的受拉性能，不考虑混凝土纤维本构中的受拉部分，从而将发生于构件端部的打开变形等效为弥散于整个构件受拉一侧的变形；②葛继平等认为在用纤维模型模拟节段拼装桥墩性能时，应采用与接缝等高的素混凝土柱来模拟接缝，但同时指出该素混凝土的材料本构选取是难点。

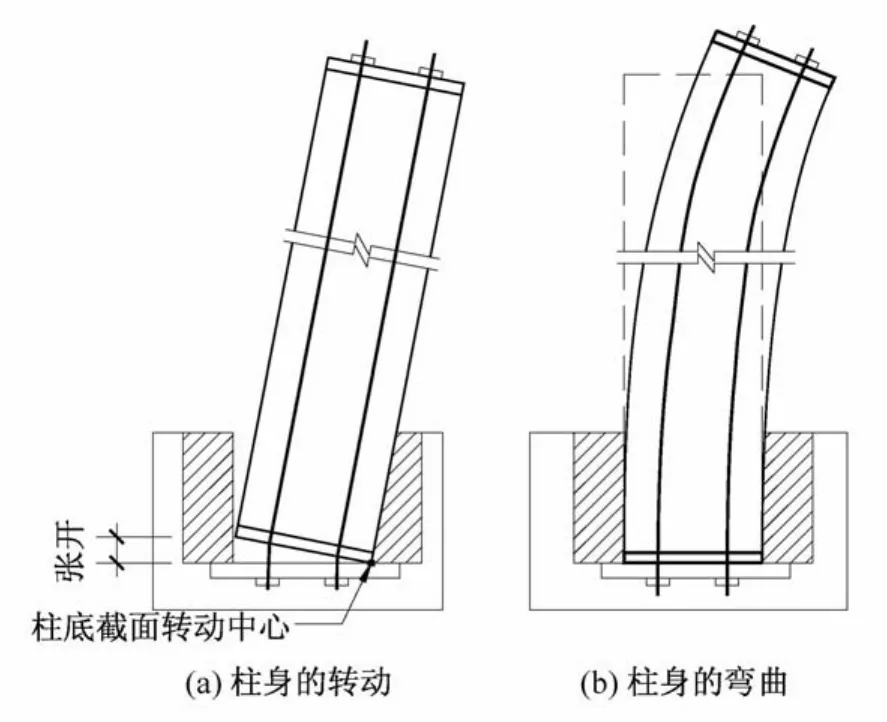
图5 自复位柱脚节点的变形模式Fig.5 Deformation pattern of self-centering column-beam joint

本文参考Zhao Jian［8］提出的模拟方法，采用ZeroLengthSection单元来反映柱脚抬升这种集中变形，ZeroLengthSection单元的截面纤维本构为单压材料本构（uniaxialMaterial ENT），以模拟柱脚与基础之间的单压特性，受压弹性模量取值为柱身混凝土材料弹模的104倍。这样处理使得ZeroLengthSection单元实际上成为只传递压力的弹性薄膜。柱脚节点的柱身由于使用的是纤维单元，强制使用了平截面假定，这样会导致弯曲构件的端部外层纤维产生巨大的应变。

如图5（b）所示，由于橡胶块位于柱脚，在柱脚处由于柱身的弯曲变形对橡胶块造成的挤压非常小，可以忽略不计。如图5（a）所示，当柱身绕柱底截面转动中心发生转动时，柱身与基础凹糟内一侧的橡胶块脱开，同时柱身开始挤压另一侧的橡胶块。由于混凝土的弹性模量远大于橡胶块，在柱身与橡胶块相互接触挤压的时候，假定柱身为刚体不发生变形，那么如图6所示，橡胶块的压缩变形可以简化为沿接触面的线性分布。类似Eluer梁的横截面变形分析（这里忽略橡胶垫块的剪切变形），橡胶块的压缩变形可以分解为轴向的压缩与绕中和轴的弯曲。因此，如图6所示可以将橡胶块离散为沿着drub方向的纤维。虽然橡胶接近完全不可压缩材料，本构关系十分复杂，但是在一定变形范围内可认为是理想线弹性材料。因此，在本文的计算分析中假定橡胶块的弹性模量为常数。此外，柱底的抗剪由柱底钢板与基础钢板之间的静摩擦力以及橡胶垫块的轴向压缩引起的反力来提供，在计算分析时假定柱底与基础之间不发生滑移。综上所述，采用如图7所示的自复位柱脚节点有限元模型。

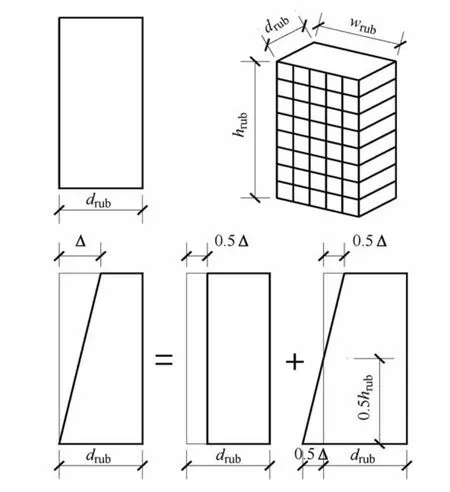
图6 橡胶块变形模式Fig.6 Deformation pattern of rubber block

3.2 梁柱节点数值模型

在梁端打开前，由于预应力筋的张拉，自复位梁端截面上的纤维均受压。自复位梁柱节点的受力性能与固接的梁柱节点没有任何区别。当梁端打开后，如图8所示，自复位梁柱节点变形可概括为：①梁绕转动中心的转动；②角钢的变形；③预应力筋的拉伸。由于预应力筋锚固于柱身，当节点打开后，梁端弯矩取决于角钢所能提供的拉力。由于顶底角钢所能提供的拉力十分有限，特别是当角钢屈服以后，因此在节点打开后，梁的受力特点更加趋近于轴压构件，这与传统框架梁的受力特点有明显的不同。此外，自复位梁柱节点的打开会导致框架的扩张（expand）。［9］框架的扩张，使得柱中线间的距离大于未扩张前柱中线间的距离。然而，由于梁内的预应力筋锚固于柱身的外侧框架的扩张又受到一定的约束。这样柱的变形将带有一定的几何非线性，几何非线性的程度与框架梁的高度有关。

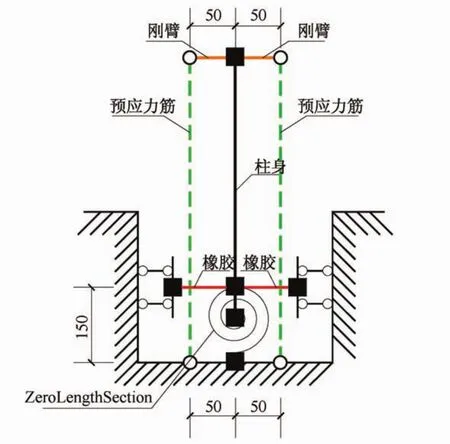
图7 自复位柱脚节点有限元模型（单位：mm）Fig.7 Finite elementmodel of the column foot（unit：mm）

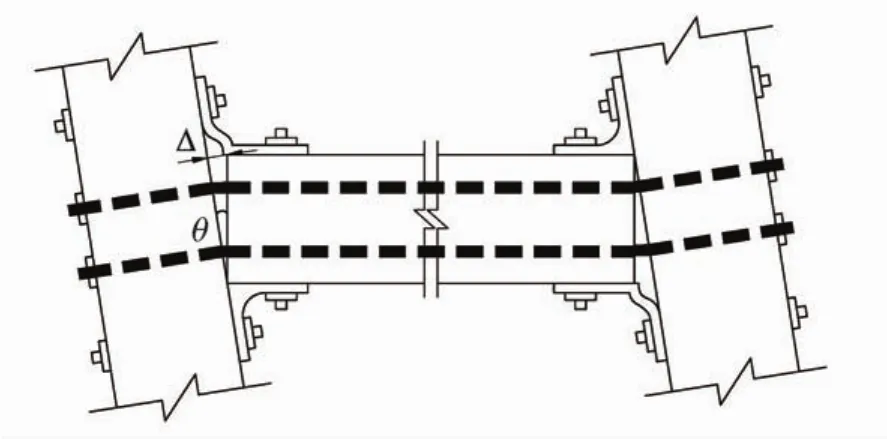
图8 自复位柱梁节点变形模式Fig.8 Deformation pattern of self-centerilg column-beam

梁柱有限元模型如图9所示，由于角钢对梁端的转动约束与梁高有关，因此梁端结点通过刚臂与角钢连接，用以考虑梁高的影响。使用Zero-LengthSection单元连接梁端与柱身。与自复位柱脚节点的模拟方法相同，ZeroLengthSection单元中截面的纤维本构采用的也是ENT Material，并将其受压弹性模量设置为混凝土弹性模量的104倍。目的在于使得梁端与柱身之间只能传递压力。

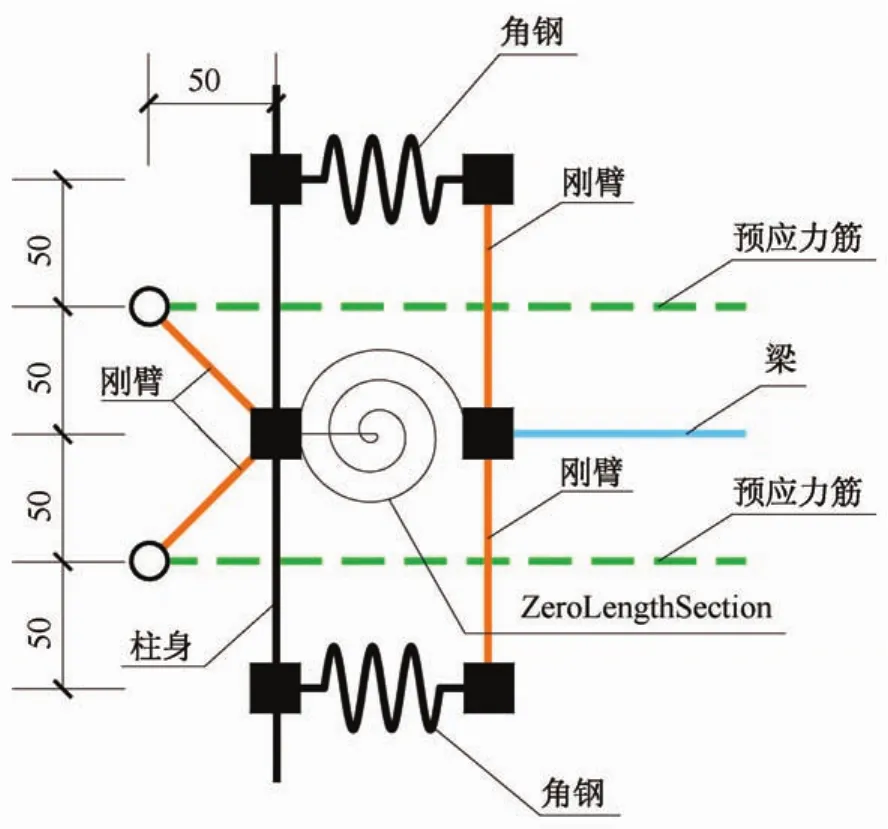
图9 自复位柱梁节点有限元模型（单位：mm）Fig.9 Finite elementmodel of self-centerilg column-beam joint（unit：mm）

本文采用OpenSEES中的ZeroLength单元来模拟角钢。角钢的本构关系采用的是Shen等［10］提出的顶底角钢拉压滞回模型。该角钢模型描述的是角钢肢跟与柱身之间的距离Δ（图8）与作用于角钢梁肢上拉力P的关系，见图10。计算分析中，ZeroLength单元的变形量就等于角钢肢跟与柱身之间的距离Δ。

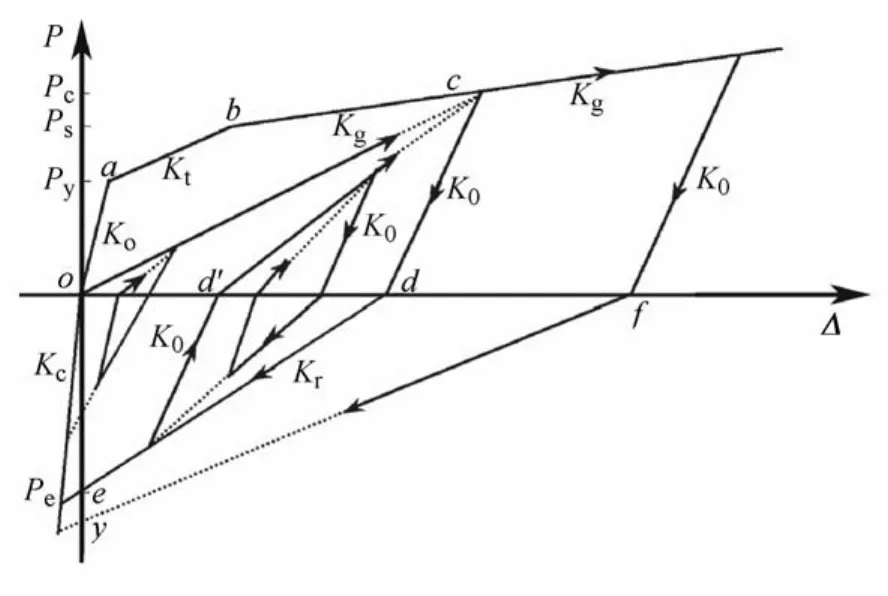
图10 角钢本构关系［10］Fig.10 Constitutive law of angle［10］

3.3 预应力筋的模拟

梁柱构件中的预应力筋为无黏结后张拉的形式，因此预应力筋并不在梁柱单元的截面中予以考虑。本文采用truss单元模拟预应力筋的轴向受力特性，每一束钢绞线只用一个truss单元模拟。预应力筋的本构采用OpenSees中的Steel02 Material。注意到Steel02 Material是可以考虑受压特性的而实际的无黏结预应力筋只能受拉。因此在进行有限元分析时，应在结果中检查truss单元是否出现了压力。本文的数值分析中，truss单元始终保持弹性受拉状态，故采用Steel02 Material是可行的。

4 振动台试验的数值模拟

本文对试验［5］的16工况和29工况进行了模拟，工况信息见表1。选择与试验相同的地震波（El Centro NS波、汶川卧龙地震台的NS波）作为地震激励输入，激励方向为X方向（坐标系见图1）。动力时程分析计算时，采用经典的Rayleigh阻尼，阻尼比设置为0.05。Rayleigh阻尼是假设阻尼与质量矩阵和刚度矩阵的组合成比例。由于在建模过程中，自复位节点处一些材料的弹性模量被设置为较大的值（如ENT Material），所以在设置阻尼时应只将Rayleigh阻尼赋予梁柱构件，否则在自复位节点处的阻尼将被不恰当地放大。

表1 工况信息Table 1 Test program g

依据上述模拟方法建立三维有限元数值模型。数值模型计算所得结构在弹性阶段前两阶频率分别为4.42 Hz与11.31 Hz。试验模型在地震波输入前使用白噪声进行扫频，实测第一阶频率为4.00 Hz，第二阶频率为11.25 Hz。对比周期可知，模拟结果中第一阶频率略有偏差，第二阶频率吻合较好。试验过程中，在动力作用下预应力筋的锚具存在一定程度的松动，每个工况后梁柱内预应力筋的内力都会下降。试验中设置力传感器监测预应力筋内力的变化，力传感器的布置如图11所示。16工况与29工况中，预应力筋的初始内力值作为时程计算分析所需的参数列于表2。

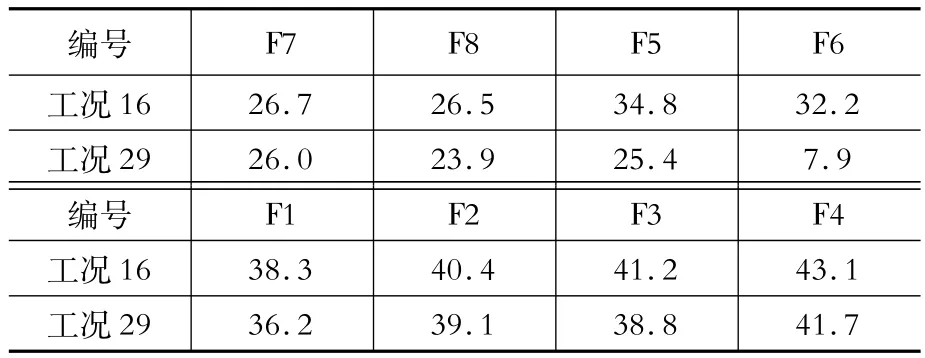
表2 预应力筋的初始内力Table 2 Initial tendon forces kN

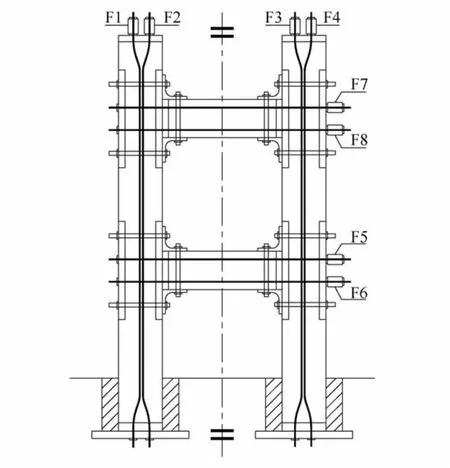
图11 力传感器位置示意图Fig.11 The location of force cell

地震动的数值模拟结果如图12—图14所示，可见数值模型对结构的位移响应，加速度响应以及柱底的抬升能够做出较为准确的预测。但是，由于使用truss单元，因此无法反映结构在动力作用下预应力筋锚具的松动引起的预应力损失。

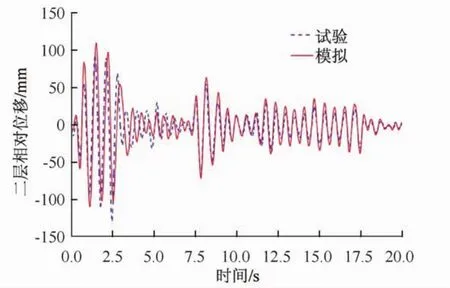
图12 工况16二层位移时程对比Fig.12 Comparison of displacement under Case 16

5 结 语

本文简要介绍了同济大学土木工程防灾国家重点实验室设计制作的自复位钢筋混凝土框架振动台试验，分析了自复位钢筋混凝土框架在地震作用下受力特点及变形模式，并介绍了自复位节点的数值模拟分析方法。通过与已有试验结果的对比，验证了数值模拟方法的可靠性。试验与模拟结果均表明，在罕遇地震下结构发生较大变形但不破坏，震后结构能够回复到初始位置，残余变形非常小。

图13 工况16二层绝对加速度时程对比Fig.13 Comparison of accelation under Case 16

图14 工况16柱底抬升时程对比Fig.14 Comparison of uplift under Case 16

图15 工况16柱预应力筋内力（F1）时程对比Fig.15 Comparison of PT force under Case 16

［1］ 周颖，吕西林.摇摆结构及自复位结构研究综述［J］.建筑结构学报，2011，32（9）：1-10.Zhou Ying，Lu Xilin.State-of-the-art on rocking and self-centering structures［J］.Journal of Building Structures，2011，32（9）：1-10.（in Chinese）

［2］ Cheok G，Lew H.Model precast concrete beam-to column connections subject to cyclic loading［J］.PCI Journal，1993，38（4）：80-92.

［3］ Priestley M J N，MACRASE G A.Seismic tests of precast beam-to-column joint subassemblageswith unbonded tendons［J］.PCI journal，1996，41（1）：64-81.

［4］ El-Sheikh M T，Sause R，Pessiki S，et al.Seismic behavior and design of unbonded post-tensioned precast concrete frames［J］.PCI journal，1999，44（3）：54-71.

［5］ 刘兢兢，吕西林，周颖，等.大比例自复位钢筋混凝土框架结构振动台模型设计与制作［J］.中国科技论文在线精品论文，2013，6（14）：1325-1332.Liu Jingjing，Lu Xilin.Zhou Ying，et al.Design and construction for a large-scale seismic model of selfcentering reinforced concrete frame［J］.Highlights of Sciencepaper Online，2013，6（14）：1325-1332.（in Chinene）

［6］ Mazzoni S，McKenna F，Fenves G.L.Open System for Earthquake Engineering Simulation（OpenSEES） User Manual.Pacific Earthquake Engineering Research Center，University of California，Berkeley，Ver.2.4.2，2013.

［7］ 吴浩，吕西林.无粘结后张拉预制剪力墙抗震性能模拟分析［J］.振动与冲击，2013，32（19）：176-181.Wu Hao，Lu Xilin.Numerical simulation on seismic performance of unbonded post-tensioned precast shear walls［J］.Journal of Vibration and Shock，2013，32（19）：176-181.（in Chinene）

［8］ Zhao J，Sritharan.S.Modeling of strain penetration effects in fiber-based analysis of reinforced concrete structures［J］.ACI Structural Journal，2007，104（2）：133-141.

［9］ Garlock M M，Sause R，Ricles JM.Behavior and design of posttensioned steel frame systems［J］.Journal of Structural Engineering，2007，133（3）：389-399.

［10］ Shen J，Astaneh-Asl A.Hysteresismodel of boltedangle connections［J］.Constructional Steel Research，2000，54：317-343.

Numerical Simulation of a Self-centering Reinforced Concrete Frame under Shaking Table Test

GAOWenjun*LU Xilin
（Research Institute of Structural Engineering and Disaster Reduction，Tongji University，Shanghai200092，China）

In order to study the seismic performance of self-centering reinforced concrete frame，a large scale modelwas designed and constructed for shaking table tests in Sate Key Laboratory of Disaster Reduction in Civil Engineering at Tongji University.The self-centering capacity of beam-column joints and column-base joints was achieved by unbonded post-tensioned tendons.Two historical ground motions，El Centro wave（1940，NS）and Wenchuan wave（2008，NS）were selected as input ground motions.Both ground motions were applied only in the X-direction.The experimental phenomena were observed and studied under different earthquake levels.In this paper，the behavior of self-centering joints under lateral load was summarized and the numericalmethod to simulate its performance was introduced.By comparing the result of the experimental results with the simulation，it was indicated that the analytical predictions agreed well with the experimental response.

self-centering reinforced concrete frame，numerical simulation，OpenSEES，shaking table test

2013-11-14

国家自然科学基金资助项目（91315301-4）

*联系作者，Email：781440618＠qq.com