基于椭球约束的载体三维磁场补偿方法

于振涛，吕俊伟，稽绍康

（海军航空工程学院控制工程系，山东烟台264001）

基于椭球约束的载体三维磁场补偿方法

于振涛，吕俊伟，稽绍康

（海军航空工程学院控制工程系，山东烟台264001）

在地磁导航中磁传感器会受到载体自身磁场的影响，为了提高磁场测量精度，需要对观测数据的载体磁场干扰进行精确补偿。在分析载体固有磁场和感应磁场数学模型的基础上，根据椭圆假设磁补偿方法的思路，提出了一种载体三维磁场干扰的补偿方法，并在椭球假设的基础上提出了载体磁场干扰补偿参数求解方法。该方法将载体磁场干扰补偿方法从二维拓展到三维，解除了载体二维运动姿态的限制。实验验证表明：该方法可以有效实现载体自身三维磁场干扰的补偿，从而提高地磁场的测量精度。

地磁导航；磁场补偿；椭球拟合；磁传感器

利用地磁场进行导航定位，具有无源、无辐射、抗干扰、全天时、全天候、体积小、能耗低的优点，因此在飞机、舰船和潜艇等领域得到广泛应用［1-2］。导航载体通过捷联式磁传感器测量空间的磁场信息，这些磁场信息不仅包括导航定位所用的地磁场信息，也包括载体自身的干扰磁场信息［2-3］。高精度的地磁导航过程中需要对磁传感器的观测磁场信息进行处理，实时对载体磁场干扰进行补偿，提高地磁导航精度。载体的自身干扰磁场主要包括载体上硬磁材料产生的固定磁场和软磁材料产生的感应磁场。

目前载体磁场干扰补偿的方法主要有基于Tolles-Lawson方程的磁补偿方法［4］和基于椭圆假设的磁补偿方法［5-7］等。美国学者Gebre E D提出了“二维磁场测量轨迹的椭圆方法”，该方法补偿精度高、算法的鲁棒性好，但计算过程复杂［8-9］。国内张晓明等在Gebre E D等的研究基础上提出了一种新型载体磁场补偿方法，该方法采用带椭圆约束的最小二乘拟合方法实现载体磁场的快速标定和各类误差统一补偿，避免了复杂的非线性参数估计和相应的迭代运算，大大降低了运算量［10］。但以上磁场干扰补偿方法都将载体运动限制在二维空间，随着三轴捷联式磁传感器在地磁导航中的应用，需要将二维的磁补偿方法拓展到三维。

本文首先对载体的固有磁场和感应磁场在载体运动过程中的特性进行分析，然后根据椭圆假设磁补偿方法的思路，提出了一种载体三维磁场干扰的补偿方法。该方法采用带椭球约束的最小二乘拟合方法保证拟合的曲面为椭球，利用磁传感器实验测量数据求取载体磁场干扰补偿参数，随后利用补偿参数对测量数据进行载体磁场干扰补偿，以消除载体自身磁场对磁观测的影响。该方法将载体磁场补偿方法从二维椭圆拟合拓展到三维椭球体拟合，解除了载体在数据拟合和补偿过程中要求水平面内运动的限制，提出了载体磁场干扰补偿参数求解方法，降低了补偿方法的运算量。

1 载体干扰磁场分析

载体在运动过程中，由于自身材料磁化和切割磁感线，进而引起诸多干扰磁场的产生，如载体固有磁场、感应磁场和涡流磁场等，其中载体的固有磁场和感应磁场对磁传感器测量的影响最大。

载体的固有磁场是由载体的硬磁材料受外磁场磁化后而产生的磁场，由于硬磁材料具有高矫顽力和剩磁值，所以一经磁化可以保留较长时间不易消失。由于磁传感器和硬磁材料都是固连在载体上的，所以不论载体姿态怎样变化，固有磁场在磁传感器3个轴上的分量是恒定的。载体的感应磁场是由载体的软磁材料被外磁场感应磁化产生的，由于软磁材料具有较低的矫顽力和较窄的磁滞回线，所以当外磁场改变时感应磁场也随之变化。感应磁场的大小及方向与载体的姿态和位置有关。以载体上捷联式磁传感器的三轴为空间直角坐标系的x、y、z轴建立载体坐标系，则固有磁场在载体坐标系中可以表示为Hh＝（Hhx，Hhy，Hhz）。根据泊松方程载体的感应磁场Hs＝（Hsx，Hsy，Hsz）可以表示为

式中：He＝（Hex，Hey，Hez）为载体坐标系中的地磁场矢量；K为载体软磁材料感应磁场系数。

综合分析载体的固有磁场和感应磁场干扰，磁传感器地磁场观测值的表达式为

地磁场进而可以表示为

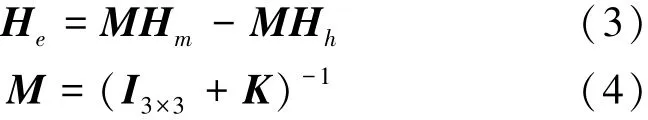
式（3）为载体磁场干扰补偿算法公式，式中载体感应磁场系数K和固有磁场Hh可以作为载体磁场干扰补偿参数。

2 载体三维磁场干扰补偿方法

2.1 地磁场测量的椭球体假设

载体在地磁场变化较小的地域内运动时，可将地磁矢量模值视为常量，即（He）THe＝const，具体表示为

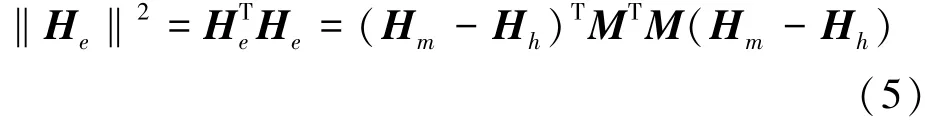
设矩阵A＝MTM／‖He‖2，则上式可表示为

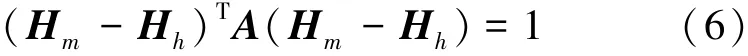
矩阵A为一个对称矩阵，可以设为

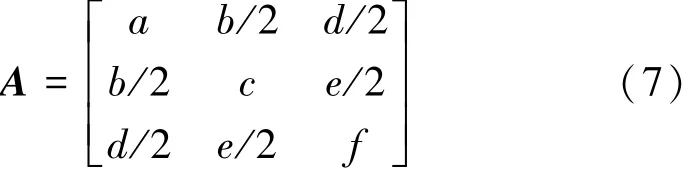
式（6）为一个椭球方程，这表明磁传感器的观测值（Hmx，Hmy，Hmz）在一个椭球面上，如图1所示。椭球的中心坐标为载体的固有磁场Hh＝（Hhx，Hhy，Hhz）。

图1 磁传感器三维观测值的椭球分布Fig.1 Ellipsoidal distribution of magnetometer 3D measured values

2.2 载体磁场干扰补偿参数求取方法

根据椭球体假设，当载体在地磁场变化较小的地域内运动时，磁传感器的地磁场观测值分布在一个三维椭球面上，设三维椭球曲面的方程为

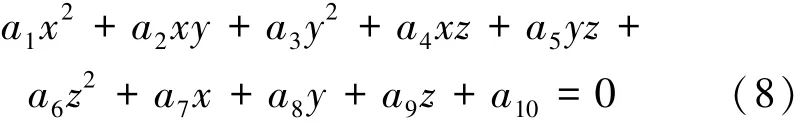
文献［10］中采用椭圆约束的最小二乘法进行椭圆拟合求取椭圆方程参数，然后通过椭圆方程参数求取载体磁场干扰补偿参数，二维椭圆方程为

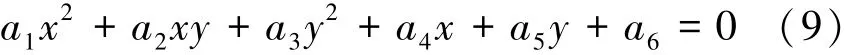
由式（8）和（9）可知，将载体干扰补偿方法由二维椭圆拟合拓展到三维椭球拟合后，方程参数由6个变为10个，如果根据文献［10］提出的方法对方程参数进行最小二乘拟合，会大大增加计算量和求解误差。本文在地磁场测量值椭球假设的基础上，提出了载体磁场干扰补偿参数载体固有磁场Hh和感应磁场系数K的求解方法，该方法首先直接利用实验观测值求取载体固有磁场Hh，然后利用最小二乘法估计剩余6个与感应磁场系数K有关的椭球方程参数。该方法将需要最小二乘估计的方程参数由10个减为6个，从而降低了计算量和提高了补偿参数求解的准确性。

2.2.1 载体固有磁场Hh计算方法

由地磁场测量的椭球假设可知，载体的固有磁场为椭球的中心坐标，因此利用关于椭球中心对称的n组观测值｛Hmi1，Hmi2｝可以求取载体固有磁场Hh，计算公式如下：

另外当观测采样点均匀分布时，可以对观测数据求平均值估计椭球中心坐标：

2.2.2 载体感应磁场系数K计算方法

椭球中心坐标Hh求出以后，设X＝Hm-Hh＝x，y，z[]T，则式（6）变为

代入对称矩阵A的表达式（7），X的三分量（x，y，z）满足以下关系式：

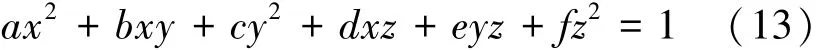
式中：a、b、c、d、e、f为互不影响的参数值。

给出n个磁传感器的观测值Hmi，可得到n个Xi。根据式（12）、（13），可得到n个线性方程组：

式中：X′＝[x2xy y2xz yz z2-1]，ξ＝[a b c d e f 1]T，矩阵A的求解可以转化为约束条件下的极值求解问题。即：

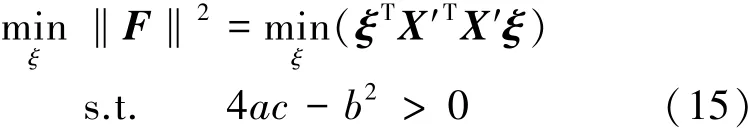
根据最小二乘估计法得到估计值ξ＾，进而求出矩阵A。对称矩阵A可以表示为A＝UTSAU，其中U为正交矩阵，SA为A的特征值组成的对角阵。因此根据A的表达式A＝MTM／‖He‖2和载体感应磁场系数K与M的关系式（4）可得K的计算公式为

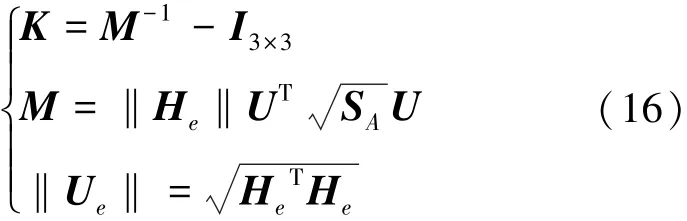
以上为载体磁场干扰补偿参数载体固有磁场Hh和感应磁场系数K的求取方法，在通过实验数据求出补偿参数Hh和K后，将补偿参数Hh和K代入载体磁场干扰补偿算法式（3），对地磁场的测量值Hm进行载体磁场干扰补偿，得到干扰补偿后的地磁场He。

3 实验

根据本文提出的基于椭球约束的载体三维磁场补偿方法，对载体磁场干扰进行补偿实验。实验分为2步：1）利用载体特定姿态的地磁场测量值求取干扰补偿参数Hh和K。2）利用补偿参数Hh和K对载体任意姿态下的地磁场测量值进行载体磁场干扰补偿，得到补偿后的地磁场值。通过载体磁场干扰补偿前后的地磁场值与真实地磁场值的比较验证本文载体三维磁场补偿方法的有效性。

3.1 补偿参数的计算

为了验证补偿方法的有效性，选取了一个空旷地域，将高精度三轴磁通门磁力仪固定在小型手动三轴无磁转台上，让磁力仪的三轴与转台的三轴重合，并以磁力仪的三轴为空间直角坐标系的x、y、z轴建立载体坐标系，以z、x、y轴旋转的角度分别为ϕ，γ，θ[]。

实验首先测量得到三轴旋转角度ϕ，γ，θ[]为［0°，0°，0°］时，地磁场的观测值为（-40 721 nT，20 085 nT，22 387 nT）。由地磁场的观测值通过计算可知：

转台三轴旋转角度ϕ，γ，θ[]为［-26.3°，0°，-153.7°］时，地磁场与x轴正方向重合。

转台三轴旋转角度ϕ，γ，θ[]为［-26.3°，0°，26.3°］时，地磁场与x轴负方向重合。

转台三轴旋转角度ϕ，γ，θ[]为［63.8°，26.3°，0°］时，地磁场与y轴正方向重合。

转台三轴旋转角度ϕ，γ，θ[]为［63.8°，-153.7°，0°］时，地磁场与y轴负方向重合。

转台三轴旋转角度ϕ，γ，θ[]为［63.8°，-63.8°，0°］时，地磁场与z轴正方向重合。

转台三轴旋转角度ϕ，γ，θ[]为［63.8°，116.2°，0°］时，地磁场与z轴负方向重合。

然后在转台上加装软硬磁材料模拟载体平台的固定磁场和感应磁场，通过实验测量以上6个特定姿态时的地磁场测量值如表1所示。

表1 载体磁场干扰下6个姿态的地磁场测量值Table 1 Six posture measured values in vehicle magnetic interferencenT

根据本文提出的载体磁场干扰补偿参数求取方法，利用表1特定姿态的地磁场测量值，载体的固有磁场Hh根据式（10）计算得到

利用表1的地磁场测量值进行最小二乘椭球拟合求取方程参数A后，再利用式（16）求出的载体感应磁场系数K为

3.2 载体磁场干扰补偿

利用载体磁场干扰补偿参数Hh和K，根据载体磁场干扰补偿公式（3），可以实现载体任意姿态下的地磁场测量值的载体磁场干扰补偿。实验测量值和干扰补偿结果如表2所示。

表2中的真实地磁场为不加装软硬磁材料的地磁场测量值。由实验结果可知，本文提出的载体三维磁场干扰补偿方法可以有效降低载体的自身磁场干扰。

表2 载体三维磁场干扰补偿实验结果Table 2 Experiment results of vehicle 3-D magnetic interference compensation nT

4 结束语

载体自身干扰磁场的实时补偿是提高磁传感器测量精度的关键技术。本文根据椭圆假设磁补偿方法的思路，提出了一种载体三维磁场干扰的补偿方法，实验表明该方法有效降低了载体的自身磁场干扰。该方法将载体磁场补偿方法由二维椭圆拟合拓展到三维椭球体拟合，解除了载体在数据拟合和补偿过程中要求水平面内运动的限制；对于由此增加的参数求取复杂难度，本文提出了干扰补偿参数求解方法，减小了运算量并提高了补偿参数求取精度。

［1］MOHAMMAD N F.Nanosatellite navigation with the WMM2005 geomagnetic field mode［J］.Turkish Journal of Environmental Sciences，2006，30（1）：43-45.

［2］周军，葛致磊，施桂国，等.地磁导航发展与关键技术［J］.宇航学报，2008，29（5）：1467-1472.ZHOU Jun，GE Zhilei，SHI Guiguo，et al.Key technique and development for geomagnetic navigation［J］.Journal of Astronautics，2008，29（5）：1467-1472.

［3］杨云涛，石志勇，关贞珍，等.地磁场在导航定位系统中的应用［J］.中国惯性技术学报，2007，15（6）：686-692.YANG Yuntao，SHI Zhiyong，GUAN Zhenzhen，et al.A magnetic disturbance compensation method based on magnetic dipole magnetic field distributing theory［J］.Aeta Armamentarii，2008，29（12）：1485-1491.

［4］TOLLES W E，MINEOLA N Y.Magnetic field compensation system：USA，2706801［P］.1955-04-19.

［5］杨新勇，黄圣国.磁航向测量系统误差修正方法研究［J］.仪器仪表学报，2004，25（4）：466-469.YANG Xinyong，HUANG Shengguo.Study of error compensation method for magnetic heading measurement system［J］.Chinese Journal of Scientific Instrument，2004，25（4）：466-469.

［6］陈棣湘，潘孟春，罗飞路.三维磁敏传感器的设计及误差分析［J］.传感技术学报，2006，19（3）：642-644.CHEN Dixiang，PAN Mengchun，LUO Feilu.Design and error analyses of 3D magnetic sensor［J］.Chinese Journal of Sensors and Actuators，2006，19（3）：642-644.

［7］FITZGIBBON A W，PILU M，FISHER R B.Direct least square fitting of ellipses［J］.IEEE Transactions on Pattern Analysis and Machine Intelligence，1999，21（5）：476-480.［8］GEBRE E D.Magnetometer autocalibration leveraging measurement locus constraints［J］.Journal of Aircraft，2007，44（4）：1361-1368.

［9］GEBRE E D，ELKAIM G H，POWELL J D，et al.Calibration of strap down magnetometers in magnetic field domain［J］.Journal of Aerospace Engineering，2006，19（2）：87-102.

［10］张晓明，赵剡.基于椭圆约束的新型载体磁场标定及补偿技术［J］.仪器仪表学报，2009，30（11）：2438-2443.ZHANG Xiaoming，ZHAO Yan.New auto-calibration and compensation method for vehicle magnetic field based on ellipse restriction［J］.Chinese Journal of Scientific Instrument，2009，30（11）：2438-2443.

A compensation method for the vehicle 3-D magnetic field based on ellipsoid constraint

YU Zhentao，LYU Junwei，JI Shaokang
（Department of Control Engineering，Naval Aeronautical and Astronautical University，Yantai 264001，China）

It is an unavoidable fact that the geomagnetic field measurement is disturbed by the magnetic field of the vehicle in geomagnetic navigation.In order to improve the measurement accuracy of the geomagnetic field，the vehicle＇s magnetic field disturbance of the observation data must be precisely compensated.Based on the induced and connatural magnetic field model of the vehicle and the compensation method under the assumed ellipse fitting，a new 3-D magnetic interference compensation method was proposed.And the calculation of the compensation parameters was put forward based on the ellipsoid hypothesis.The proposed method improves the magnetic interference compensation from the 2-D ellipse fitting to the 3-D ellipsoid fitting，and relieves the restriction on the 2-D motion of the vehicles.Finally，the experimental results show that the proposed method can compensate for the 3-D magnetic interference of the vehicle efficiently and improve the measurement accuracy of the geomagnetic field.

geomagnetic navigation；magnetic field compensation；ellipsoid fitting；magnetic sensor

10.3969／j.issn.1006-7043.201302013

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201302013.html

V241.62

A

1006-7043（2014）06-0731-04

2013-02-22.网络出版时间：2014-05-14 15：51：12.

国家863计划资助项目（2010AAJ211）.

于振涛（1984-），男，博士研究生；吕俊伟（1962-），男，教授，博士生导师.

于振涛，E-mail：shouguangyzt＠163.com.