基于模型预测控制的动力定位过驱动控制设计

梁海志，李芦钰，欧进萍，3

（1.大连理工大学运载工程与力学学部，辽宁大连116024；2.大连理工大学建设工程学部，辽宁大连116024；3.哈尔滨工业大学土木工程学院，黑龙江哈尔滨150090）

基于模型预测控制的动力定位过驱动控制设计

梁海志1，李芦钰2，欧进萍2，3

（1.大连理工大学运载工程与力学学部，辽宁大连116024；2.大连理工大学建设工程学部，辽宁大连116024；3.哈尔滨工业大学土木工程学院，黑龙江哈尔滨150090）

半潜式平台动力定位系统仅能控制纵荡、横荡和艏摇的低频运动，而整个系统安装的推力器个数大于被控自由度个数，因此整个定位系统为过驱动系统。针对该系统，采用模型预测控制，将虚拟控制力计算和推力分配实现一体化设计。控制力由推力器推力显式表达，充分考虑了推力器物理性能，以推力器推力变化率为控制参数。设计中，首先利用当前运动状态预测环境扰动，通过最小二乘法实现环境扰动的初次分配，然后再进行标准模型预测控制，充分考虑了桨-桨干扰造成的推力损失问题，通过设置上下游推力器间推力夹角，有效地避免了推力损失。最后给出数值算例验证了该方法。

半潜式平台；动力定位；过驱动系统；模型预测控制；扰动补偿；约束控制；推力分配；推力损失

随着海洋工程向深海发展，传统的锚泊定位由于经济成本和铺设难度增加等原因，不再适用于深水海洋平台。取而代之，动力定位系统逐渐在深水海洋工程中得到广泛采用。动力定位系统于20世纪60年代提出，最开始主要应用于钻井船等对定位要求较高的浮式结构物中，而后逐渐在其他深水浮式结构物中得到广泛采用。为了降低系统能耗和避免推力器不必要的磨损［1］，动力定位系统仅对浮体水平面内3个自由度（纵荡、横荡和首摇）的大幅慢漂响应进行控制。

动力定位系统按功能，一般分为3个部分［2-3］：上层导航系统，中间层控制力和推力分配系统和底层推力器控制系统，在设计过程中分别针对各个部分进行模块化设计。针对系统中的各个部分，已有大量文献分别对其进行了研究。在对控制力研究中，最早提出的是PID控制，该方法简单易行，但是对其控制参数的调节较为困难，并且鲁棒性不强。随着状态空间的出现，现代控制算法LQG［4］等被广泛采用。除此以外，滑模控制［5］、反步法［6］等非线性控制算法也有研究。针对推力分配法，主要方法有伪逆法［7］、二次规划法［8］等。

采用模块化设计虚拟控制力时，若不考虑推力器性能，在推力分配时虚拟控制力常会超出推力器允许范围，使推力分配时无法准确分配控制力，进而使整个系统达不到理想设计状态。本文综合考虑动力定位系统中的控制系统与分配系统，将其视为过驱动系统，充分考虑定位能力和定位精度，即控制输入和状态受约束情况。已有大量文献［9］针对过驱动系统受约束问题展开研究，主要有抗积分饱和法（anti wind-up）和模型预测控制等。模型预测控制由于受计算硬件限制计算效率较低，在动态响应较慢的化工领域内可使用在线控制［10］，而响应较快的问题则需事先进行离线计算、然后进行在线控制；但随着计算硬件水平大幅提高，逐渐在航空［11-12］、船舶［13-16］等领域的在线控制中得到应用。

本文采用模型预测控制，将虚拟控制力直接由推力器推力显式表达，并将模型预测性能指标中的控制力指标等效为推力器能量消耗，基于推力分配计算控制力。在标准的模型预测控制中，无法考虑扰动项，因此需提前补偿外部扰动，本文采用文献［14］提出的方法，利用当前运动状态预测环境扰动，并充分考虑推力器物理性能和推力损失，同步实现推力计算和推力分配。

1 半潜式平台动力方程

在随船坐标下，根据牛顿第二定律水平面内零航速线性化低频运动方程为［1］

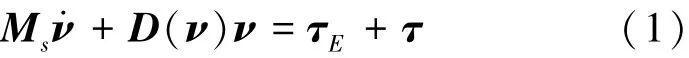
式中：ν为速度向量，ν＝[vxvyvψ]T；Ms为平台质量矩阵（含转动惯量），由自身质量和低频附加质量构成，Ms＝M+Ma；D为低频阻尼系数矩阵；τE为环境载荷；τ为控制力（含控制弯矩），τ＝[τxτyτrz]T。在定位模式下，由于平台的速度近似为零，因此可认为矩阵Ms和D中的水动力系数为常数：

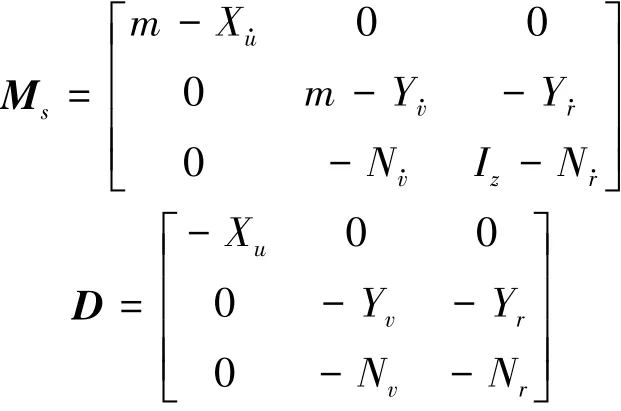
式中：m为平台质量，Iz为转动惯量。

在半潜式平台中，动力定位系统一般采用全回转推力器，该推力器可以360°全方位出力。在推力分配算法中［3］，一般以推力器出力角α和推力幅值Ti作为优化变量，本文为了使控制力可由推力器推力显式表达，在笛卡尔坐标系下将推力Ti分解为Tix和Tiy，如图1所示，则控制力表达为

式中：Fth为推力器推力向量；BCA为推力重构矩阵。若推力系统由N个推力器构成，则Fth＝与此对应的BCA＝推力器布置如图2所示，(Lxi，Lyi)为第i号推力器位置坐标。

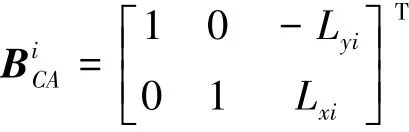
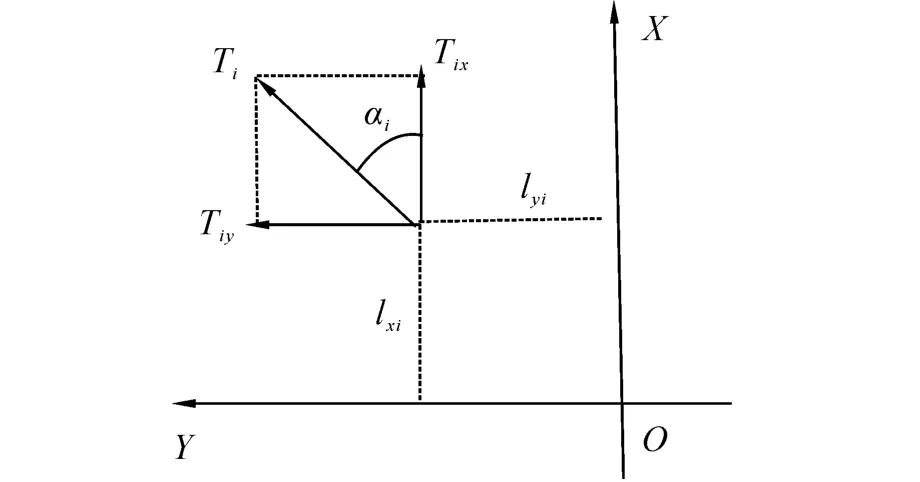
图1 推力器推力示意图Fig.1 Diagram of axial thrust

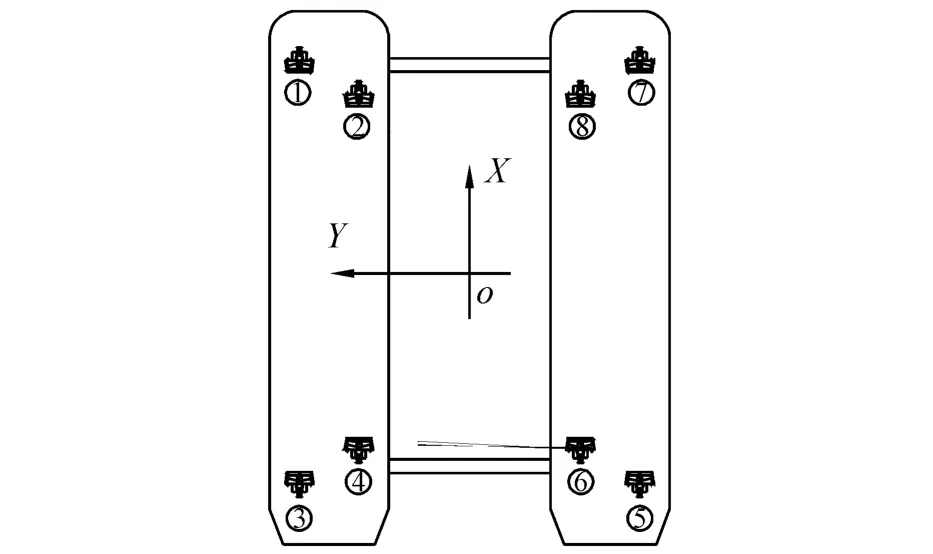
图2 推力器布置Fig.2 Propellers′arrangement

将式（2）代入式（1），并将其改写为状态方程后得

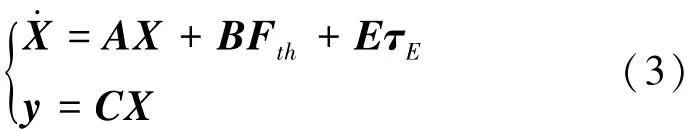
3 动力定位系统模型预测控制

标准模型预测控制问题的离散控制系统为

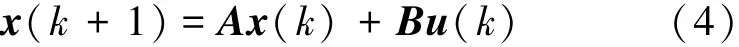
式中：x为状态向量，u为控制向量。

对于动力定位系统，若仍按式（4）的标准模型预测进行控制时，如果系统（式（4））受到扰动，得到的控制力将违背状态约束条件Xlb＜Cx( k+j+1|k )＜Xub。本文采用文献［14］中提出的方法，首先补偿环境扰动，将式（3）转化为标准模型预测控制。在补偿环境载荷时，通过k时刻运动状态预测k-1时刻的环境扰动，即

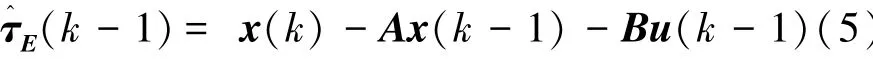
式中：x（k）、x（k-1）分别为k和k-1时刻的状态，在预测中认为，采样时间足够短，则k时刻的环境载荷τ＾

E（k）可由k-1时刻的τ＾E（k-1）在误差允许的范围内近似。

由式（5）得到的环境载荷，通过优化方法，实现载荷初次分配。在分配过程中，首先需考虑推力器间相互影响引起的推力损失问题。将处于同一浮箱上彼此距离较近的2个推力器分为一组，如图2所示，1号和2号分为一组，其余的以此类推。当下游推力器处于上游推力器的尾流中时（如图3所示），若此时2个推力器的推力方向平行，则从Dang等［17］总结的桨-桨干扰推力损失模式经验公式中可看出，该情况中下游推力器的推力损失最严重。固定桨间距，考虑相对夹角变化时的推力损失经验公式：

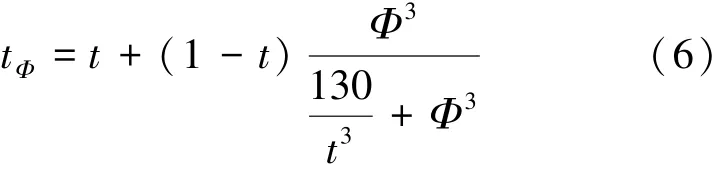
式中：Φ为2螺旋桨之间的相对夹角，t为固定螺旋桨桨间距，Φ＝0时的推力减额系数［17］。从式（6）中可看出，当发生推力损失时，为了降低该不利影响，可设置推力夹角。当推力器1（或2）的推力方向处于阴影中时，如图4所示，相应的下游推力器2（或1）则完全处于尾流中。在推力分配中，以推力器是否处于该区域为依据，判断是否发生推力损失，若发生，则设置推力器间的夹角为其次，为了减少推力器磨损并充分考虑推力器物理性能，在分配过程中，以推力幅值变化Δu为控制参数，对其施加约束后，得

式中：du-为Δu约束上限，Δui＝。除此以外，还需对推力角变化率Δα-进行约束，即Δαi≤Δα-。综上要求，对载荷进行初次分配时以Δu为优化参数，控制系统转化为以下优化问题：

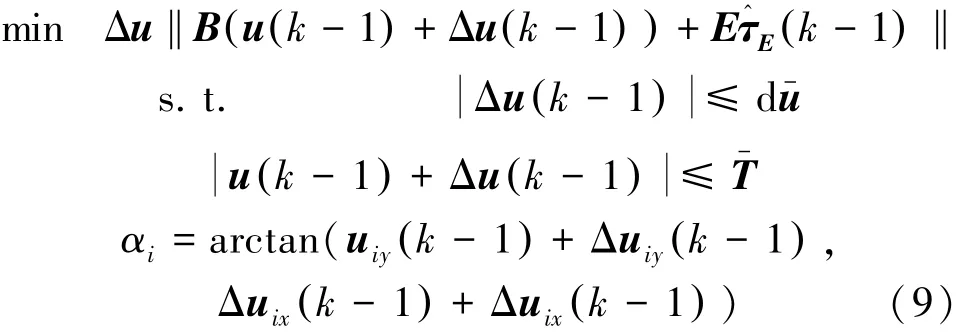
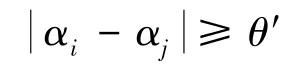
式中；i、j为发生推力损失时对应组中的推力器编号；θ′为最小推力夹角，可根据系统定位和能耗要求，通过式（6）取值。

对环境载荷进行补偿后，式（3）转为标准的模型预测控制问题，优化目标为

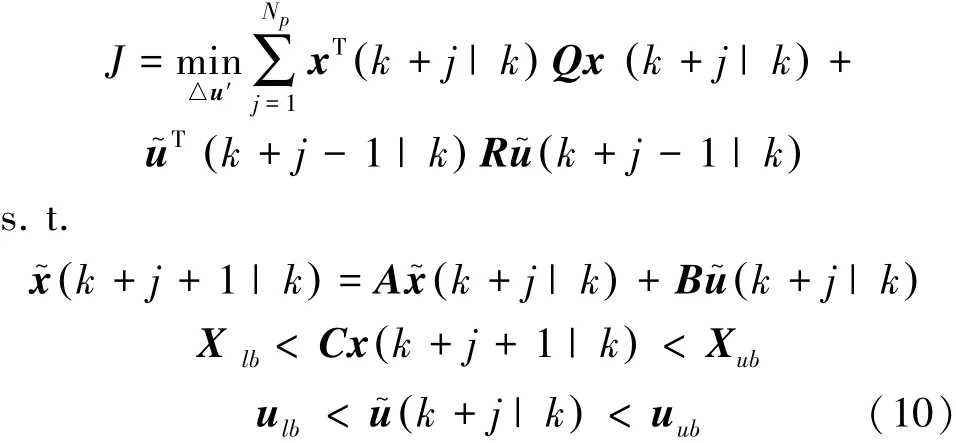
式中：Xlb和Xub分别为状态约束；ulb和uub为控制力约束；u～为控制力输入；Q和R分别为状态和控制力的权值矩阵。对于控制力输入，由于推力器首先补偿了环境载荷，并且在执行控制时，采用滚动时域法仅执行第一步控制力，因此在模型预测控制中控制力约束需对控制力约束修正为

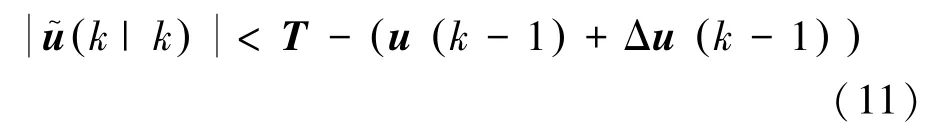
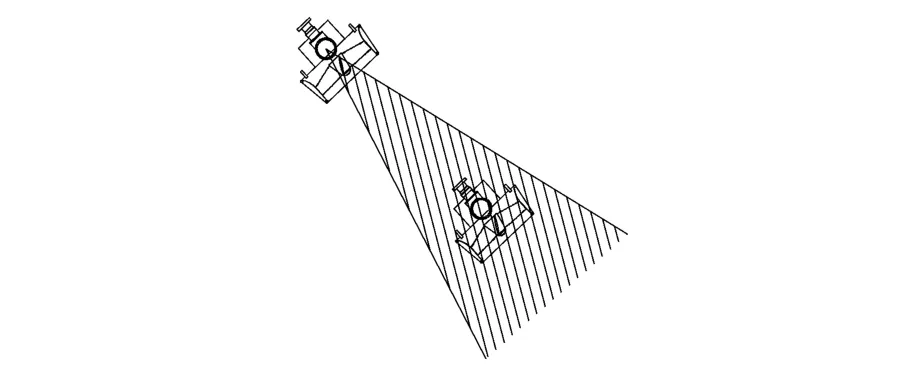
图3 桨桨干扰推力损失示意图Fig.3 Diagram of thrust loss between propellers

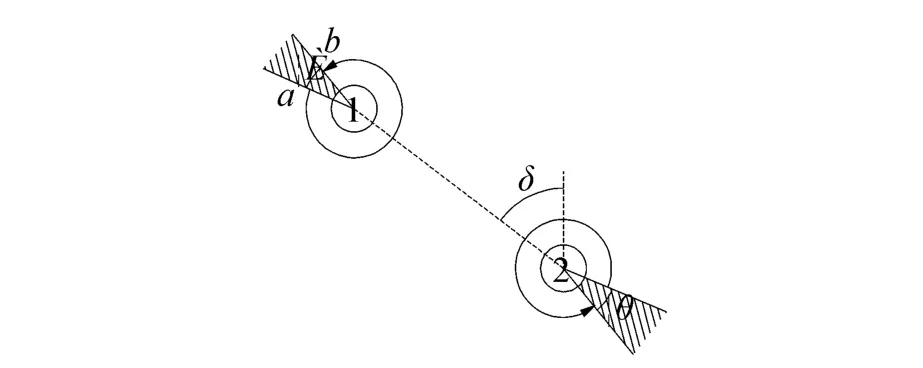
图4 推力器出力角示意图Fig.4 Propellers’thrust direction zone

4 数值仿真

本文以HYSY-981半潜式平台为研究对象，该平台最大作业水深为3 000 m，由2个浮箱、4根立柱、上甲板及其它建筑物构成。该平台设计为水深在1 500 m内时采用锚泊定位，当水深大于1 500 m时采用动力定位，本文选择的设计水深为1 500 m。

对于深海平台受到的环境载荷为风、浪和流，对于风载荷一般采用前馈控制［4］，因此本文只考虑波浪和海流载荷，但须注意的是推力器需为风载荷留出推力余量。本文采用的动力方程仅针对低频运动，因此波浪力中只包含了引起大幅慢漂低频运动的二阶波浪力。海流载荷采用模块法进行计算。波浪载荷采用JONSWAP谱，有义波高为6.0 m，谱峰周期为11.2 s，峰形系数为2.0，波浪力入射方向为45°。海流速度为1 m／s，与波浪入射方向相同。

选择W-B4-70导管螺旋桨作为推力器，考虑推力冗余度设Tmax＝550 kN，Tmin＝0 kN，螺旋桨转速变化率为±0.2 s-2，则推力变化率范围为ΔT＝±3.0 kN／s。推力器推力角转动速率为±1（°）／s［18］。为了降低推力损失，本文通过采用错位布置增加推力器间距，如图2所示。当相邻推力器间的出力夹角θ′设为18°，下游推力器推力减额系数由式（6）计算得到为0.882 5，若继续增加θ′并不能大幅提高减额系数，因此本文将θ′设为18°。

在模型预测控制中，预测步长Np＝8，优化权值设为Q＝diag（100，100，100），R＝diag（1 000）1×16。为了保证钻井立管的安全，动力定位系统的定位要求一般为水深的2%～3%，本文为了验证算法的有效性，水平面内的位移约束为1.5 m，艏摇转角为5°。图5给出的是位移时程曲线，图5中实线为平台的真实位移，虚线为名义系统位移。从图中可看出，尽管名义位移满足设定要求，但是平台的真实位移并不满足设定约束。其产生的原因是，动力定位系统的主要功能是提供抵抗环境荷载，由于推力器性能受限，主要包括推力幅值变化量和总的推力幅值受限，造成推力器无法提供足够的控制力来完全抵消环境载荷，由此带来了定位误差。图6给出了控制力时程曲线。

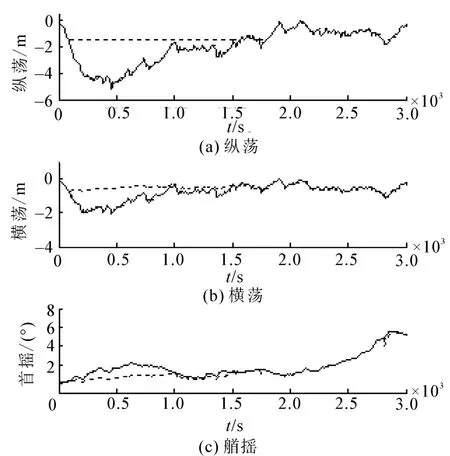
图5 位移时程曲线Fig.5 Time-history of displacements

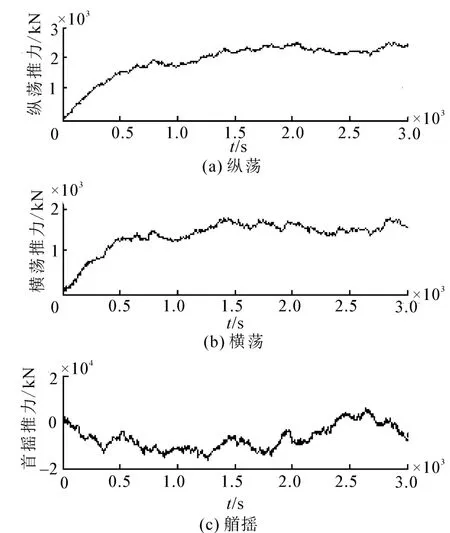
图6 控制力时程曲线Fig.6 Time-history of control forces

图7 为1号推力器推力时程曲线，分别给出了1号推力器x、y方向的推力分量和总的推力幅值T，从图中看出推力器幅值满足推力要求，即未超出设定的最大推力幅值550 kN。图8给出的是1号推力器推力变化量时程曲线，图8（a）为x、y方向的分量，图8（b）为推力增量幅值，其均满足约束条件。从图7中还可看出，尽管推力器最大推力幅值仍比较充裕，但是考虑到推力器的磨损及发电机的负荷，对推力器单位时间内的推力变化量施加约束，使推力器无法实时地提供理想推力，由此造成了图5中纵荡位移超出了预先设定目标。本文为了验证算法对约束的作用，因此设置的位移约束比较保守，从位移时程曲线可看出控制结果满足水深2%～3%的要求。当半潜式平台遭遇恶劣海况或对定位要求较高时，可以适度放宽对推力器推力变化增量的约束，从而使动力定位系统的适用范围更广，并保证钻井平台作业的安全性。

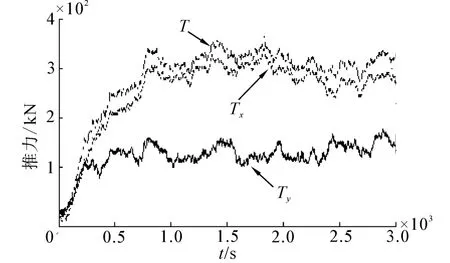
图7 1号推力器推力时程曲线Fig.7 Time-history of thrust of No.1 propeller

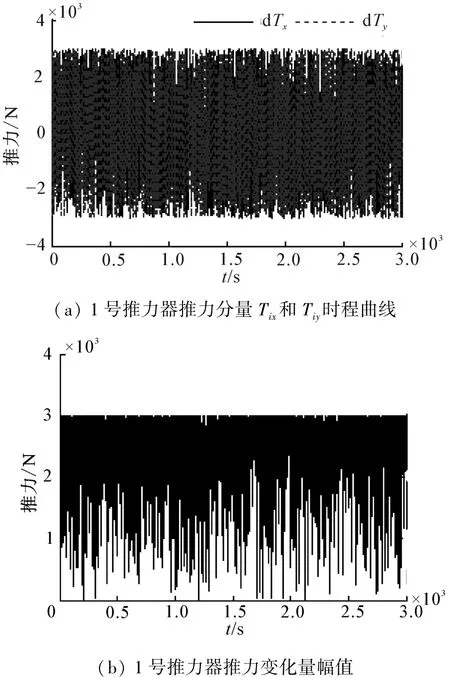
图8 1号推力器推力变化量时程曲线Fig.8 Time-history of No.1 propeller’s thrust

图9 为第1组推力器的推力角时程曲线。当1号推力器的尾流完全覆盖2号推力器时，1号推力器的推力角为55°。为了尽可能的避免下游推力器的推力损失，设置1号推力器造成的2号推力器损失影响域（即图4中1号推力器的阴影部分）为［37.5°，73.5°］。当1号推力器推力角处于该区域时，推力角约束（式（7））发挥作用，以避免2号推力器推力损失。当发生推力损失情况时，推力器1与2间的推力夹角可从图9中明显观察到。从第500 s开始，2号推力器尾流对1号推力器的影响较弱，此时1号与2号出力方向基本一致。换言之，当推力器间不受桨-桨干扰影响时，每组推力器基本以相同方向共同抵抗环境载荷。图10为推力角变化量，可看出在模拟初始阶段，1号和2号推力器为到达理想运行状态，推力器在满足最大推力变化前提下，推力夹角变化量较明显，但随着模拟时间的增加，推力器出力角变化量运行逐渐减小，并达到理想状态。

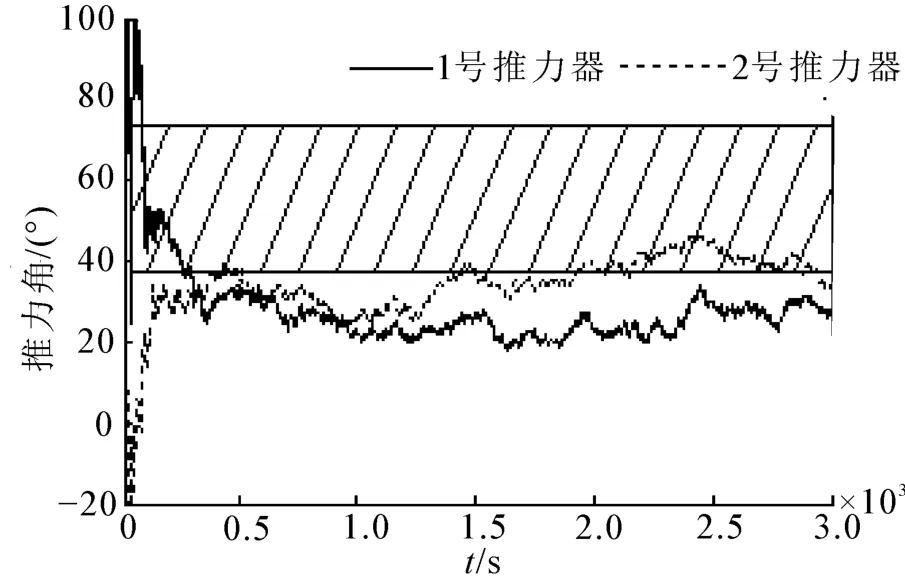
图9 推力器推力角时程曲线Fig.9 Time-history of thrust angles

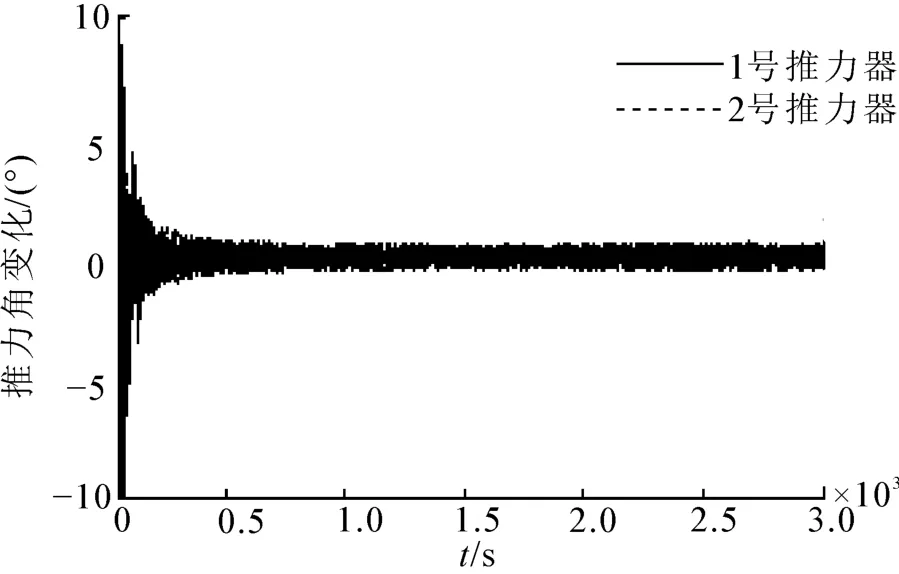
图10 推力器推力角变化量Fig.10 Time-history of thrust angles’change

5 结论

本文基于模型预测控制法，由推力器推力显式表达控制力，将动力定位系统考虑为过驱动系统，实现控制力计算和分配一体化，得到以下结论：

1）采用模型预测控制，对平台的运动状态和控制输入施加约束，采用当前运动状态预测环境载荷，使原问题转化为标准模型预测控制；

2）将控制力由推力器推力显式表达，实现控制力和推力分配同时在线计算，较传统的级联模块化设计，可避免由于受推力器性能的限制，推力分配算法无法精确分配控制力而造成的平台定位失位情况，尤其是对于开环控制器；

3）在控制力计算中，充分考虑推力器间因桨-桨干扰造成的推力损失问题，定义了发生推力损失时的推力角区间，通过设置推力夹角，一方面可有效地避免推力损失，另一方面可避免传统推力分配法中存在的可行域非凸问题。

［1］FOSSEN T I.Guidance and control of ocean vehicles［M］.Hoboken：Wiley，1994：307-321.

［2］FOSSEN T I，JOHANSEN T A.A survey of control allocation methods for ships and underwater vehicles［C］／／14th Mediterranean Conference on Control and Automation.Ancona，Italy，2006：1-6.

［3］JOHANSEN T A，FOSSEN T I，BERGE S P.Constrained nonlinear control allocation with singularity avoidance using sequential quadratic programming［J］.Control Systems Technology，2004，12（1），211-216.

［4］SØRENSEN A J，SAGATUN S I，FOSSEN，T I.Design of a dynamic positioning system using model-based control［J］.Control Engineering Practice，1996，4（3）：359-368.

［5］TANNURI E A，AGOSTINHO A C，MORISHITA H M，et al.Dynamic positioning systems：an experimental analysis of sliding mode control［J］.Control Engineering Practice，2010，18（10）：1121-1132.

［6］FOSSEN T I，GRØVLEN A.Nonlinear output feedback control of dynamically positioned ships using vectorial observer backstepping［J］.IEEE Transactions on Control Systems Technology，1998，6（1）：121-128.

［7］SHI J，ZHANG W，LI G.et al.Research on allocation efficiency of the redistributed pseudo inverse algorithm［J］.Science China Information Sciences，2010，53：271-277.

［8］HÄRKEGÅRD O.Dynamic control allocation using constrained quadratic programming［J］.J Guidance，Control and Dynamics，2004，27：1028-1034.

［9］MAYNE D Q，RAWLINGS J B，RAO C V，et al.Constrained model predictive control：stability and optimality［J］.Automatica，2000，36：789-814.

［10］YANG W，STEPHEN B.Fast model predictive control using online optimization［J］.Control Systems Technology，2010，18（2）：267-278.

［11］ALEXIS K，NIKOLAKOPOULOS G，TZES A.Switching model predictive attitude control for a quadrotor helicopter subject to atmospheric disturbances［J］.Control Engineering Practice，2011，19：1195-1207.

［12］LIU Cunjia，CHEN Wenhua，ANDREWS J.Tracking control of small-scale helicopter using explicit nonlinear MPC augmented with disturbance observers［J］.Control Engineering Practice，2012，20：258-268.

［13］王元慧，施小成，边信黔.基于模型预测控制的船舶动力定位约束控制［J］.船海工程，2007，29（3）：22-25.WANG Yuanhui，SHI Xiaocheng，BIAN Xinqian.Restriction control of marine dynamic positioning system based on model predictive control［J］.Ship Engineering，2007，29（3）：22-25.

［14］LI Zhen，SUN Jing.Disturbance compensating model predictive control with application to ship heading control［J］.Control Systems Technology，2012，20（1）：257-265.

［15］CHEN Hongli，WAN Lei，WANG Fang，et al.Model predictive controller design for the dynamic positioning system of a semi-submersible platform［J］.Journal of Marine Science and Application，2012，11：361-367.

［16］王元慧，隋玉峰，吴静.基于非线性模型预测的船舶动力定位控制器设计［J］.哈尔滨工程大学学报，2013，34（1）：110-115.WANG Yuanhui，SUI Yufeng，WU Jing.Marine dynamic position system based on nonlinear model predictive control［J］.Journal of Harbin Engineering University，2013，34（1）：110-115.

［17］DANG J，LAHEIJ H.Hydrodynamic aspects of steerable thrusters［C］／／Dynamic Positioning Conference.Houston，USA，2004.

［18］吴显法，王言英.动力定位系统的推力分配策略研究［J］.船海工程，2008，37（3）：92-96.WU Xianfa，WANG Yanying.Design of the thrust allocation for the dynamic positioning system［J］.Ship and O-cean Engineering，2008，37（3）：92-96.

Over-actuated controller design for dynamic positioning system based on model predictive control

LIANG Haizhi1，LI Luyu2，OU Jinping2，3
（1 Faculty of Vehicle Engineering and Mechanics，Dalian University of Technology，Dalian 116024，China；2.Faculty of Infrastructure Engineering，Dalian University of Technology，Dalian 116024，China；3 School of Civil Engineering，Harbin Institute of Technology，Harbin 150090，China）

The dynamic positioning system（DPS）of the deepwater semi-submersible platform can only control lowfrequency motions of surge，sway and yaw.DPS can be considered as an over-actuated system，because the number of propellers is more than the horizontal plane degrees of freedom.Model predictive control（MPC）which integrates the virtual control force calculation and thrust allocation was adopted.The control forces were explicitly expressed by the propellers＇thrust forces，which fully considered the propellers′physical performance，and the thrust change rate was considered as the control parameters.In the design，the environment disturbance was predicted firstly based on the current dynamic states，achieving the initial distribution of environmental perturbations by using the least squares method.And then the standard model predictive control was done，which takes full consideration of the thrust loss due to thrust-thrust interaction problems.It effectively avoided thrust loss by setting the thrust angle between the upstream and downstream thrusters.Based on these designs，while the virtual control forces are gotten，they are allocated directly.Finally the effectiveness of the algorithm is verified.

semi-submersible platform；dynamic positioning；over-actuated system；model predictive control；disturbance compensator；constrained control；thrust allocation；thrust loss

10.3969／j.issn.1006-7043.201305031

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201305031.html

U661.1

A

1006-7043（2014）06-0701-06

2013-05-10.网络出版时间：2014-05-14 15：50：15.

国家973计划资助项目（2011CB013702；2011CB013703）；创新研究群体科学基金资助项目（51221961）.

梁海志（1984-），男，博士研究生；欧进萍（1959-），男，教授，博士生导师，院士.

梁海志，E-mail：mr_liangok＠163.com.