EMD与样本熵在往复压缩机气阀故障诊断中的应用

张思阳，徐敏强，王日新，高晶波

（1.哈尔滨工业大学航天学院，黑龙江哈尔滨150001；2.中国石油哈尔滨石化分公司，黑龙江哈尔滨150056）

EMD与样本熵在往复压缩机气阀故障诊断中的应用

张思阳1，2，徐敏强1，王日新1，高晶波1

（1.哈尔滨工业大学航天学院，黑龙江哈尔滨150001；2.中国石油哈尔滨石化分公司，黑龙江哈尔滨150056）

针对往复压缩机气阀故障信号冲击性、非连续性特点，采用EMD方法分解提取各频率故障信号。然后通过对数据重新筛选、提出主要振动信息对分解波形进行了重构。并对往复压缩机故障信号分解及重构数据进行了分析，提取了故障信息。针对正常与故障信号分解结果复杂度不一致的特点，对EMD分解后包含的故障信息主要分量进一步通过样本熵进行量化识别。最后通过对正常、阀片缺口、弹簧失效的实测信号进行EMD分解、重构和样本熵分析，精确提取了故障信息，验证了方法的有效性。

往复压缩机；压缩机气阀；经验模态分解；气阀故障；信息重构；量化分析；样本熵

往复压缩机大多数故障都属于气阀故障。由于往复压缩机气阀故障信号非连续性、冲击性及不具备全局性的特点，采用传统的傅里叶变换、基于时频的故障分析往往难于找到故障特征。因此局部信号分析方法得到广泛开展，如针对气阀早期故障，魏中青、李刚等［1-2］采用最大似然估计及双演化遗传聚类算法等方法提取故障特征。Fengshou Gu等［3］提出用改进的双频谱来提纯信号，防止信号干扰用来诊断气阀的泄漏问题。M.H.El-Ghamry［4］等根据不同的统计特征和识别模式采用不同时间窗对声发射信号进行分析。Zhigang Chen［5］等提出采用信息熵作为特征提取参数，提取小波包熵作为输入载体，并基于支持向量机（SVM），提出了新的向量机方法较传统BP算法得到了极大改进。李月［6］等针对混叠噪声提出采用结合余弦信号2次EMD［7］处理方式，对地震信号进行了探究。由于往复压缩机气阀信号的复杂性、混乱性和数据量的巨大，使得通过往复压缩机气阀原始信号进行故障诊断难度较大。为了能够去除噪声干扰，需要对数据进一步的处理，使信号故障特征明显。文章通过采用经验模态分解方法［7-8］（empirical mode decomposition，EMD）把信号数据分频段分析，通过提取不同频段内的故障振动特征，突出某一频段的故障。并进一步收集必要信息，对数据进行重构，形成新的振动波形。为了进一步定量分析往复压缩机故障，从EMD分解的IMF分量中选取包含故障主要信息的前几个内蕴模式分量的样本熵［9-10］对机组故障进行量化分析。

1 经验模态分解方法

首先对往复压缩机的基本结构进行分析，从中得出故障类型。通过对故障类型及采集的信号特点阐述，并根据EMD自身的多频率段分解特点，选取EMD作为此类问题的分析工具。通过对机组故障信息进行分析，阐述此类故障适合EMD分析。

分析流程见图1。

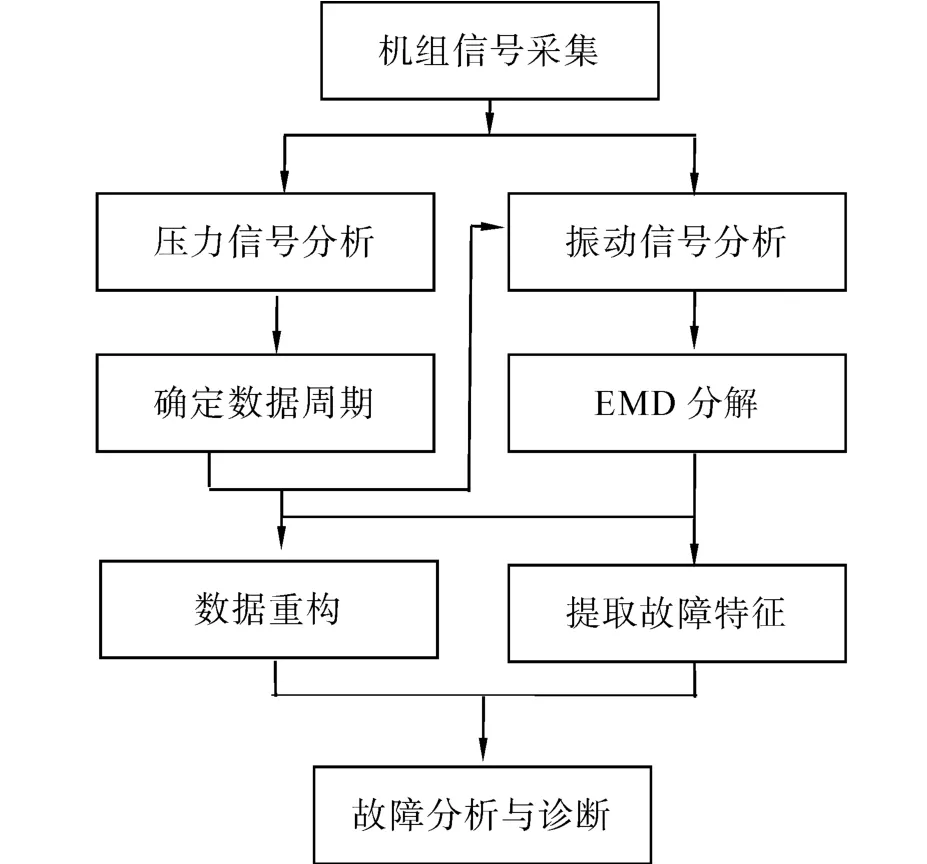
图1 分析流程图Fig.1 Analysis tree

EMD方法是把一个复杂的非平稳振动信号分解为有限个基本模式分量（IMF）之和。其中任何一个基本模式分量在整个数据段内极值点的个数和零交叉点的个数相等或相差不超过1个；在任一点，由局部极大值点形成的包络线和由局部极小值点形成的包络线平均值为零。选取往复压缩机的振动信号x（t）进行分解。基本步骤如下：

1）确定实际振动信号x（t）各局部极值点；

2）采用三次样条曲线构造x（t）的极大值点和极小值点，并建立极大值点包络线lmax和极小值点包络线lmin；

3）计算上、下包络线的平均值包络线lm；

4）用原数据x（t）减去平均包络线的值得到去掉低频成分的新数据序列：h（t）＝x（t）-lm，重复步骤1）～4），直到h（t）满足停止条件，即取得的平均包络趋向于零，得到了第1个IMF分量c1（t），表示信号的最高频成分。

5）然后用x（t）减去c1（t）得到一组新的序列r1（t）。再重复上述步骤得到一系列的ci（t）和最后一个不可再分的rn（t）。

则得到：

由于每一个IMF的信号包含了从高到低的不同频率段的成分，并且ci（t）为平稳信号。

EMD是一种对非平稳信号进行自适应分解的方法，通过将信号按不同尺度的波动或趋势进行逐级分解，产生一系列具有不同特征尺度的数据序列，每一个序列称为一个固有的模态函数IMF。EMD的基本实现过程是用“筛分”的方法把一个复杂信号分解为有限个本征模函数之和。

2 往复压缩机气阀故障分析

2D12-70／0.1-13型往复对称双缸压缩机布置见图2。针对2D-12型往复式压缩机正常工况、阀缺口故障、阀弹簧故障情况下采集的振动数据进行分析，利用EMD分析找到不同频段的故障特征，查找机组运行中存在的问题，量化故障，拾取有价值信号进行重构，降低信号噪声影响，提高故障分析的准确性。

图2 一、二级阀的布置图Fig.2 First and second valve structure picture

图2 中定义空间坐标方向如下：x为活塞轴线方向由二级缸指向一级缸，y为曲轴轴线方向由外指向内，z方向为垂直于地面向上方向。测点序号后面的x、y、z代表传感器安装方向。12个振动测点为加速度传感器，分别布置在缸盖及缸头上。设置故障为二级排气4 g阀中间阀片有2个缺口，二级排气3 g阀少弹簧。同步采集数据包括多通道振动加速度相信号等。为了保证数据具有可比性，测点均选在二级盖侧近排气阀位置。

选取一个完整周期的振动信号绘制原始波形图，如图3所示。

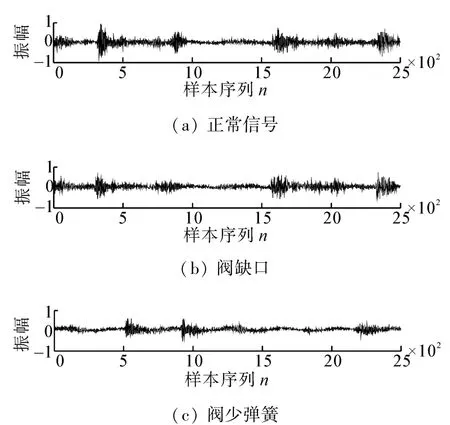
图3 原始信号波形Fig.3 The original signal wave form

由于该波形含有各种干扰及噪声信号，如气流脉动及如图2中十字头、齿轮箱部件、电机运行等振动干扰。由于电机及齿轮箱部件转速高于往复压缩机的活塞往复次数，十字头则表现为在方向发生变化时出现脉冲振动于是存在着干扰信号与故障信号时频的不同。根据EMD分解信号的特点，可以提取不同时频段的振动信息，适合分析此类故障。

针对原始信号多种频率混叠及噪声干扰的情况，采用EMD对图3（a）、（b）、（c）3种信号进行分解，结果见图4～6。

图4 正常状态下EMD变换Fig.4 The EMD transform of normal signal

图5 阀缺口状态下EMD变换Fig.5 The EMD transform of valve gap

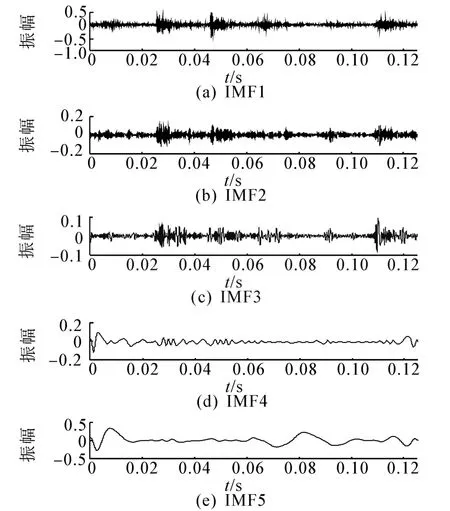
图6 阀少弹簧状态下EMD变换Fig.6 The EMD transform of valve less spring

如图3（a）是正常全周期信号的原始振动波形，数据与图5中的一个周期数据对应。由于噪声及干扰信号的存在，造成信号相关信息度降低，影响测试精度及分析。图3（b）阀缺口故障，与图6（a）正常运行状态的原始振动波形相比未发现明显故障特征。图3（c）为阀少弹簧故障，与图6（a）相比，波形比较散乱，吸排气阀打开及闭合信息完全被淹没在低频信号中。无法确认整个运行过程中，吸、排气阀的开启与闭合状态。

图4～6中，每个IMF的3个图分别对应阀正常状态、阀缺口故障、阀少弹簧故障EMD分解结果。根据选取的往复压缩机故障信号特征，仅取前5个包含故障信息较多的分量进行分析。IMF1～IMF5分别表示特征频率由高到低的EMD分解分量，纵轴表示相对振动幅值。

根据故障分解情况，IMF6以后的波形失真严重，且振动相对幅值的数量级明显下降（分解结果略）。为了进一步确认分解后波形的降噪及故障特征提取能力，选择故障信息较多的IMF1～IMF5的数据进行振动波形重构，重构结果见图7。

虽然原始波形比较混乱，但经过EMD分解后从IMF分量可以识别各级频率的振动特点，如高频冲击，低频扰动现象。通过信号重构图形中可以看出，经过重构后信号信息更为丰富，机组故障信息表达更加清楚。

下面对3种状态进一步具体分析。

1）正常运行状态的振动波形经分解后吸气阀打开时冲击最大，振动主要集中在高频IMF1、IMF2阶段，IMF3以后振动幅值显著降低。

2）阀片缺口故障状态下由于排气阀漏气，膨胀及吸气时由于出口气体重新漏回到气缸内造成吸气阀吸入的气量较少，由于气缸内压力下降较慢，造成了吸气阀打开较正常时间延长、同时由于在吸气阶段排气阀继续漏气，造成气缸内气体压力上升较快，吸气阀吸气时间缩短，关闭提前且振动幅值较小。因此IMF分量低频幅值高于正常状态，吸气阀打开滞后，关闭提前。

3）排气阀少弹簧故障，在未进行EMD分解及重构时，吸、排气阀打开与关闭的冲击及低频扰动现象均不明显，从各级分解结果上看，在高频阶段，吸、排气阀冲击明显，表现出了吸、排气阀的打开与关闭现象。同时低频幅值明显上升，说明低频扰动情况严重，从重构结果及IMF4、IMF5发现少弹簧故障阀片低频扰动特征比较明显。

图7 重构信号波形Fig.7 Reconstruction of signal wave forms

3 样本熵分析

样本熵是一种与近似熵相类似但精度更高的复杂性度量方法，通过样本熵可以对数据的复杂度进行量化分析。

一般地，对于由N个数据组成的时间序列{x（n）}＝x（1），x（2），..，x（N），样本熵（sample entropy）的基本定义为

式中：m表示组成的时间序列向量的维数值，r表示样本熵距离阈值，N表示数据总数。根据数据特点，取m＝2，r＝0.15 sd，sd表示原始数据的标准差。计算3种状态IMF1～IMF5分量样本熵，具体样本熵量化结果见表1及图8。

表1 样本熵量化结果Table 1 The quantity results of SE

图8 IMF样本熵Fig.8 SE of IMF

经过将EMD分解后的数据通过样本熵量化可以识别出不同故障特征。正常状态相对于故障状态样本熵值较高，说明正常状态信号复杂度高。正常状态各级EMD分解总体的样本熵值逐渐下降，说明频域高的信号复杂度高。阀缺口及阀少弹簧2种故障存在不同的复杂度升高现象，反映出不同故障表现的频域不同。

4 结束语

由于传统时频域分析方法对非平稳信号可调能力较差，信号经处理后故障特征表现不清晰。针对此种信号特点，通过EMD变换，进一步结合样本熵分析，对往复压缩机采集的正常信号及2种故障振动信号分析。通过正常数据及故障数据的各IMF对比，表明在不同频域可以表现出不同的故障特征，并采用含信息量较大的数据重构波形。重构后的振动波形相比于原始信号，故障特征清晰。通过IMF分解、信号重构及样本熵方法的综合分析为往复机组的气阀故障诊断提供了可靠的信息。经采用上述方法后准确识别出了往复压缩机气阀缺口、阀少弹簧故障。

［1］魏中青，马波，窦远，等.基于MLE阈值规则的小波特征提取技术在气阀故障诊断中的应用［J］.振动与冲击，2011，30（1）：237-241.WEI Zhongqing，MA Bo，DOU Yuan，et al.Wavelet feature extracting technique based on maximum likelihood estimation threshold rule and its application in fault diagnosis of a gas valve［J］.Journal of Vibraton and Shock，2011，30（1）：237-241.

［2］李刚，庄健，侯洪宁，等.往复压缩机气阀早期故障的双演化遗传聚类检测［J］.振动、测试与诊断，2010，30（4）：384-388.LI Gang，ZHUANG Jian，HOU Hongnin，et al.The double action genetic algorithm clustering on the initial failure of reciprocating valve［J］.Journal of Vibraton Measurement and Diagnosis，2010，30（4）：384-388.

［3］GU Fengshou，SHAO Yimin.Motor current signal analysis using a modified bispectrum for machine fault diagnosis［C］／／ICROS-SICE International Joint Conference.Fukuoka，Japan，2009：4890-4895.

［4］EL-GHAMRY M H，REUBEN R L，STEEL J A.The development of automated pattern recognition and statistical feature isolation techniques for the diagnosis of reciprocating machinery faults using acoustic emission［J］.Mechanical Systems and Signal Processing，2003，17（4）：805-823.

［5］CHEN Zhigang，LIAN Xiangjiao.Fault diagnosis for valves of compressors based on support vector machine［C］／／Chinese Control and Decision Conference.Xuzhou，China，2010：1235-1238.

［6］李月，彭蛟龙，马海涛，等.过渡内蕴模态函数对经验模态分解去噪结果的影响研究及改进算法［J］.地球物理学报，2013，56（2）：626-634.LI Yue，PENG Jiaolong，MA Haitao，et al.Study of the influnce of transition IMF on EMD denoising and the improved algorithm［J］.Chinse J Geophys，2013，56（2）：626-634.

［7］HUANG N E.The empirical mode decomposition and the Hilbert spectrum for nonlinear and nonstationary time series analysis［C］／／Proc R Soc Lond A.Greenbelt，USA，1998，454（4）：903-955.

［8］YANG J N，LEI Y，LIN S，et al.Hilbert-Huang based approach for structural damage detection［J］.Journal of Engineering Mechanics，2004，1：85-95.

［9］苏文胜，王奉涛，朱泓，等.基于小波包样本熵的滚动轴承故障特征提取［J］.振动、测试与诊断，2011，31（2）：162-166.SU Wenshen，WANG Fengtao，ZHU Hong，et al.Feature extraction of rolling element bearing fault using wavelet packet sample entropy［J］.Journal of Vibration，Measurement and Diagnosis，2011，31（2）：162-166.

［10］赵志宏，杨绍普.一种基于样本熵的轴承故障诊断方法［J］.振动与冲击，2012，31（6）：136-140，154.ZHAO Zhihong，YANG Shaopu.Sample entropy-based roller bearing fault diagnosis method.［J］.Journal of Vibration and Shock，2012，31（6）：136-140，154.

Application of EMD and SampEn to the fault diagnosis of reciprocating compressor valves

ZHANG Siyang1，2，XU Minqiang1，WANG Rixin1，GAO Jingbo1
（1.School of Astronautics，Harbin Institute of Technology，Harbin 150001，China；2.PetroChina Harbin petrochemical Company，Harbin 150056，China）

Aiming at the characteristics of fault signals of for a reciprocating compressor valve：shock and discontinuity，the EMD method was taken to decompose and extract the fault signal of every frequency，which was reconstructed through screening the data and finding the main vibration information.The decomposition results and reconstruction data of the reciprocating compressor fault signals were analyzed，and the fault information was extracted.For the complexity of decomposition results of the normal and fault signal，the sample entropy（SampEn）method was used to quantitatively analyze the fault information of every main IMF.EMD combined with reconstruction，and SampEn methods were applied to analyze the vibration signals of three kinds of conditions：normal state，valve gap，and valve less spring.The practical application abstracted the fault information exactly and proved the feasibility of the proposed method.

reciprocating compressor；compressor value；empirical model decomposition（EMD）；valve faults；information reconstruction；quantitative analysis；sample entropy（SampEn）

10.3969／j.issn.1006-7043.201308008

http：／／www.cnki.net／kcms／doi／10.3969／j.issn.1006-7043.201308008.html

TH457；TP206.3

A

1006-7043（2014）06-0696-05

2013-08-03.网络出版时间：2014-05-14 15：53：27.

国家自然科学基金资助项目（10772061）.

张思阳（1971-），男，高级工程师；徐敏强（1965-），男，教授，博士生导师.

张思阳，E-mail：z90sy＠163.com.