快速反演算法在汽轮机蒸汽湿度测量中的应用

刘芳艳，黄竹青，2*，曹小玲，蔡 成，杨 颖

（1.长沙理工大学能源与动力工程学院，长沙410114；2.湖南有色金属职业技术学院，株洲412006）

快速反演算法在汽轮机蒸汽湿度测量中的应用

刘芳艳1，黄竹青1，2*，曹小玲1，蔡 成1，杨 颖1

（1.长沙理工大学能源与动力工程学院，长沙410114；2.湖南有色金属职业技术学院，株洲412006）

为了解决汽轮机通流部分蒸汽湿度的在线测量问题，提出了一种基于散射相函数的半经验公式快速反演散射光强分布的计算方法。该算法采用MATLAB自带的cftool进行相函数的双高斯拟合，拟合误差低，且拟合函数可以快速得到Mie散射理论的近似解析解，即从散射光强分布到水滴质量中间半径的快速反演。结果表明，在约束水滴粒径范围内，得到了颗粒大小与散射比之间的半经验模型，对比实验测得散射比，吻合良好，且由半经验模型反演得到水滴质量中间半径为1.1μm。在一定条件下，可以有效解决蒸汽湿度的在线测量问题。

散射；水滴质量中间半径；双高斯拟合；汽轮机

引 言

汽轮机低压缸常期在湿蒸气状态下运行，在湿蒸气流过叶片时，会造成腐蚀，影响机组经济、安全运行，降低汽轮机级效率。而对水滴粒径的在线测量，对于实现汽轮机蒸汽湿度测量，以适时调整汽轮机组蒸汽进口参量，提高机组运行的安全性和经济性具有重要意义。

自20世纪70年代以来，流动蒸汽湿度的测量技术才取得了较大进展。随着激光技术、光电技术及计算机技术的迅速发展和广泛应用，基于激光散射法测量颗粒粒径分布［1］的技术得到了广泛应用。由于激光散射法［2-4］具有适用性广、粒径测量范围宽、测量准确、精度高、重复性好、测量速度快、所需知道的被测颗粒及分散介质的物理参量少、仪器的自动化及智能化程度高、可实现在线测量等优点，同样被应用于汽轮机水滴粒径的测量中［5-6］。

传统的水滴粒径的测量方法是基于Mie散射理论，通过对测量得到的前向小角度散射光强分布进行反演［7］实现的。然而经典Mie散射理论计算量大，且要经过大量迭代，非常耗时，不能满足实时测量的要求。因此，本文中提出了一种基于散射相函数的半经验公式快速反演散射光强分布的算法，并采用MATLAB内置命令cftool对水滴群散射相函数进行双高斯拟合，得到散射相函数近似的半经验公式，从而建立起水滴粒径分布与散射光强之间的快捷桥梁，为测量汽轮机低压缸的蒸汽湿度，提供了快速可行的方案。采用参考文献［8］中的实验图像，分析得到与散射光强分布关联的实验散射比，验证了数值模拟结果。

1 M ie理论与MATLAB数值模拟

在经典Mie散射理论的基础上，运用参考文献［8］中的改进算法，充分利用MATLAB的内置命令与函数集，可以实现散射系数、消光系数、散射相函数在任意较宽颗粒粒径范围内的快速计算。非偏振光情形下，散射光强表示式为［8］：

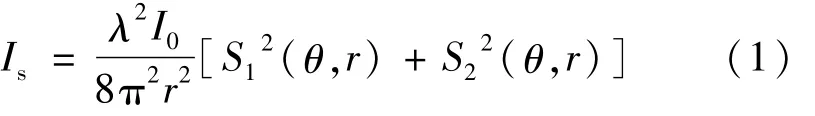
式中，Is为总散射光强，I0为入射光强，λ为激光波长，r为颗粒半径，S1（θ）和S2（θ）为振幅函数。

将水滴质量中间半径代入（1）式可数值模拟散射光强值的分布情况。但其逆向解，即实验测得散射光无法应用文献方法求得水滴质量中间半径。在汽轮机通流部分蒸汽湿度在线测量要求下，需寻求Mie散射理论解可替代近似公式。

2 相函数的双高斯拟合

Mie氏理论在已知散射光强条件下，反演颗粒粒径分布时，其矩阵为变态矩阵，没有解析解。因此，为了获得散射光强的逆向解，这里将水滴的散射相函数作双高斯拟合，得到拟合公式——半经验公式。其中，散射相函数是散射光强随散射角度变化的函数。

［9］中的改进Mie计算方法下，得出散射相函数计算式。当入射光为非偏振光时，其表达式为：

式中，p（θ，r）为散射相函数，θ为散射角，r为颗粒尺寸半径，m为两相介质相对折射率（因两相介质相对稳定，这里不做讨论为激光波数，Qsca（r，m）为散射系数，rmax和rmin为水滴半径的最大值及最小值，f（r）为水滴尺寸分布概率密度函数。f（r）服从罗辛-拉姆勒（Rosin-Rammler，R-R）分布，该分布函数特别适合于描述喷雾形成的液滴群，在一定范围内是可靠的，其表达式为：

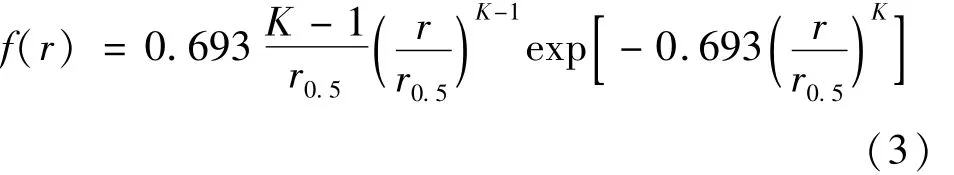
式中，r0.5为水滴质量中间半径，K为水滴分布的宽度参量。

采用MATALB编程，分别计算了不同波长、水滴质量中间半径下散射相函数图像随角度变化关系曲线，如图1和图2所示。从图中可知：（1）波长越短，散射现像越明显，且主要集中在前向小角度；（2）水滴质量中间半径越大，散射现象越明显，在前向小角度集中分布，且在较大角度处振荡明显。

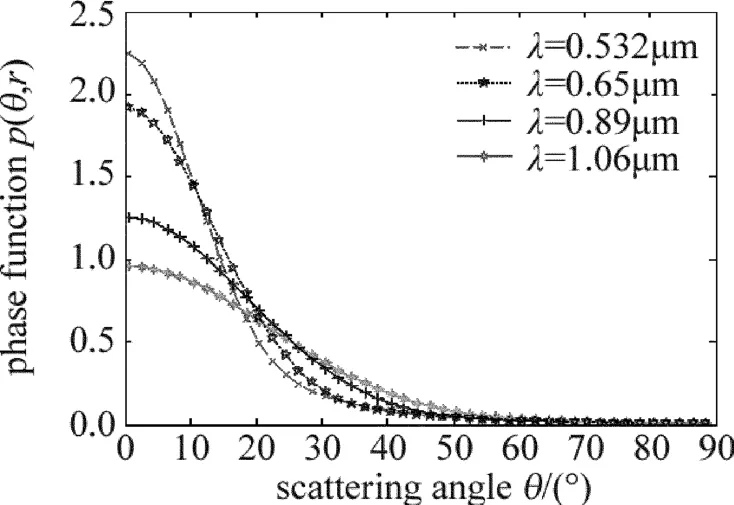
Fig.1 Phase function under differentwave length of scattering

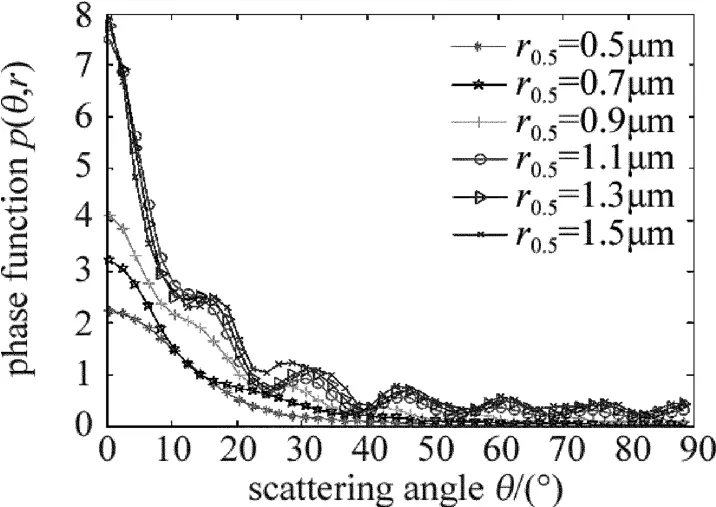
Fig.2 Phase function under differentwater qualitymiddle radius

可见，影响散射光强分布的因素很多，且水滴质量中间半径是影响蒸汽湿度测量的关键因素。在汽轮机低压缸中，一次水滴粒径范围在0.1μm～2μm之间，取水滴质量中间半径范围为0.5μm～1.5μm，假定其它参量为定值，如λ＝0.532μm，K＝5，结合（2）式数值模拟r0.5＝0.5μm时散射相函数图像，如图3所示，同时采用MATLAB内置命令cftool及函数集在同一图像上进行高斯拟合及双高斯（double Gaussian）拟合。拟合结果显示，采用双高斯函数拟合结果更为理想。

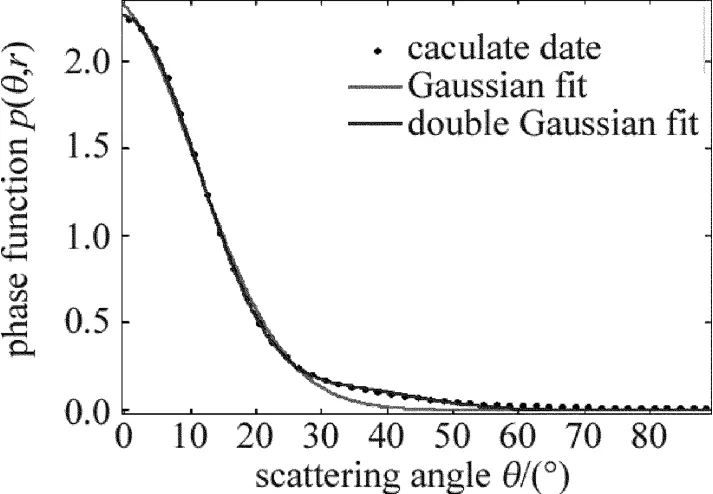
Fig.3 Gaussian fitting and double Gaussian results for phase function

经MATALB内置命令cftool及编程所得双高斯拟表达式，即相函数近似半经验公式：

式中，α1，β1，γ1，α2，β2和γ2均为拟合待定参量，p′（θ，r，λ）拟合散射相函数。显然参量与激光波长、水滴质量中间半径r0.5等因素有关。当λ取0.532μm，0.65μm，0.89μm，1.06μm时，得到的拟合特定参量与波长相关关系如图4所示，由于实验条件及波长的可控因素，仅对λ＝0.532μm进行分析。r0.5在0.5μm～1.5μm范围内时，拟合参量与半径相关关系如图5所示。

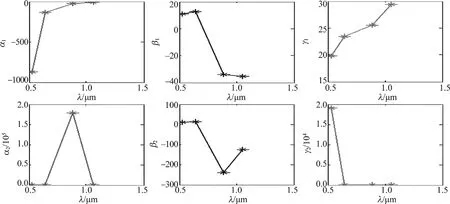
Fig.4 Double Gaussian fitting parameters changing with the laserwavelength

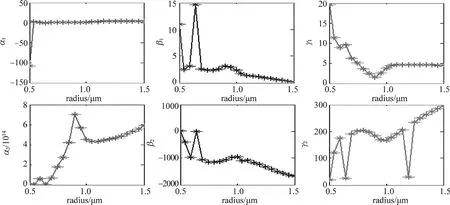
Fig.5 Double Gaussian fitting parameters changing with water qualitymiddle radius

假设散射角为θ时，散射光强为I（θ），拟合散射相函数为p′（θ，r，λ）；散射角为θ0时，散射光强为I（θ0），拟合散射相函数为p′（θ0，r，λ）。可得如下散射比Ks关系式：

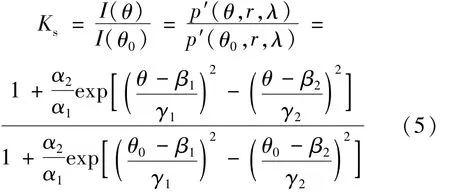
在实验测得散射光强灰度图像条件下，经转化得不同散射角θ＝3.4°～5.6°，θ0＝3.2°下，散射光强比值，根据半经验公式（4）式，应用图4中双高斯拟合参量随水滴质量中间半径变化关系，便可计算得到水滴质量中间半径r0.5。以此半径代入经典Mie散射理论，数值模拟得散射光强值

3 散射比结果分析

在MATLAB开发环境下，为了检测cftool自带双高斯函数反演方法的可靠性，用参考文献［10］中对模拟汽轮机低压缸平台实验所摄CCD灰度图像进行分析，并提取灰度曲线，如图6所示。实验结果表明，在散射角θ＝3.2°时，灰度值最强，随后灰度值迅速下降。

Fig.6 Forward small angle scattering intensity distribution and the axial grayscale

实验中测得散射比以后，利用相函数半经验公式推导出的散射比关系（5）式及相函数拟合参量点进行反演［10］，计算在背压为0.50MPa下，可得湿蒸气的水滴质量中间半径为1.1μm。将水滴质量中间半径代入（1）式，经Mie理论数值模拟得理论散射比，结果如表1所示。

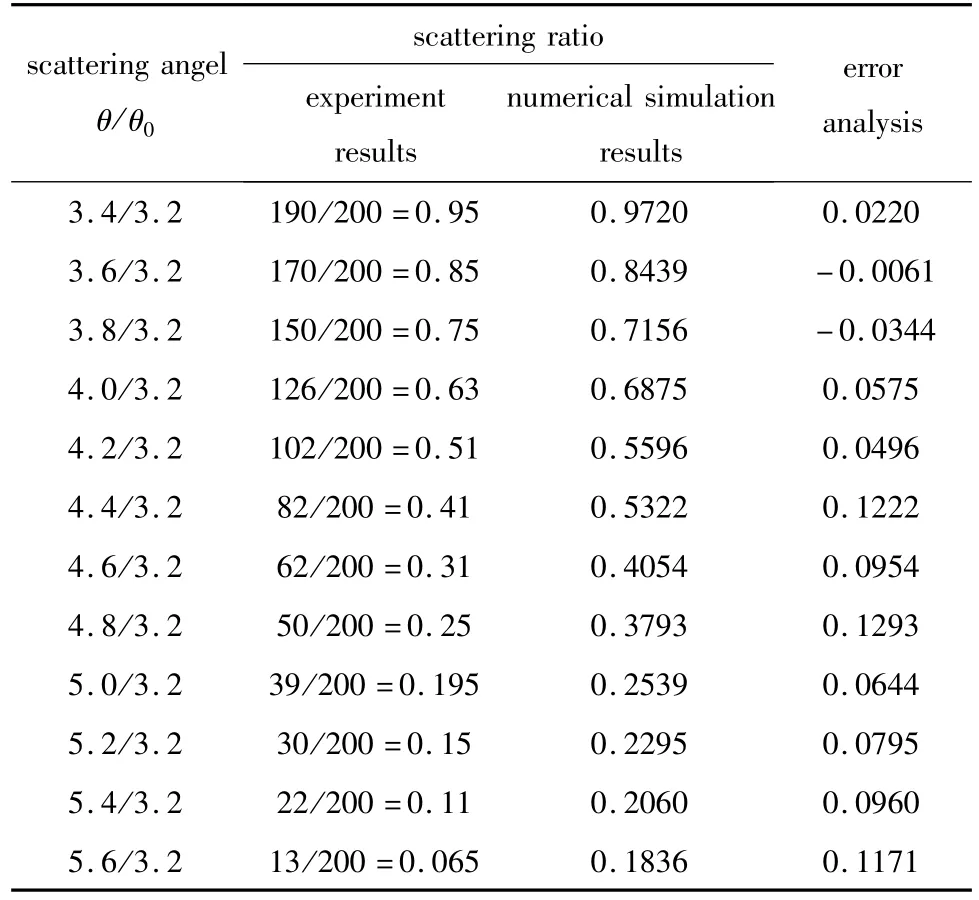
Table1 Under different scattering angle，the scattering ratio results between the experiment and Gaussian fitting

从表1可以看出，由于受大角度孔径光阑的限制及环境和测量误差等因素的影响，在散射比为时，实验值较理论值要小。但总的来说，经半经验公式反演简化后，数值模拟散射比结果与实验测得结果吻合良好。

实验测得多组散射比，代入（5）式，求出拟合参数值，由拟合参量与水滴质量中间半径关系，可求得水滴质量中间半径为r0.5＝1.1μm，采用半经验公式数值模拟结果与参考文献［11］中用经典Mie散射理论计算结果相近，说明该方法有效。将反演r0.5＝1.1μm代入以下两式，便可对汽轮机通流部分蒸汽湿度Y进行计算［8］：

式中，Vm为单位体积内的水滴总容量，n（r）为尺寸分布函数；vm是饱和水的比容，vs是饱和汽的比容，均可通过查表获取。

4 结 论

针对经典Mie散射理论测量颗粒粒度大小时没有严格解析解情形，这里用MATLAB自带cftool对相函数进行双高斯拟合，得出相函数半经验公式，使Mie理论解变得简单、快速可解。实验中测得散射比，经半经验公式反演得到水滴质量中间半径为1.1μm，再用于散射相函数数值模拟，计算得散射比。

可以说所求得半径即为模拟汽轮机低压缸内水滴颗粒质量中间半径。

与其它算法相比，其优点表现在：（1）计算简单，数值模拟结果与实验结果吻合较好；（2）可以实现汽轮机通流部分蒸汽湿度在线测量问题；（3）具有一定的理论意义和工程实际应用价值。

参考文献

［1］ KADONO T，ARAKAWA M，KOUCHIC A.Size distributions of chondrules and dispersed droplets caused by liquid breakup：An application to shock wave conditions in the solar nebula［J］.Icarus，2008，197（2）：621-626.

［2］ SIGEL R.Light scattering near and from interfaces using evanescentwave and ellipsometric light scattering［J］.Colloid＆Interface Science，2009，14（6）：426-437.

［3］ GOGOIA，BURAGOHAIN A K，CHOUDHURY A，et al.Laboratorymeasurements of light scattering by tropical fresh water diatoms［J］.Journal of Quantitative Spectroscopy＆Radiative Transfer，2009，110（14／16）：1566-1578.

［4］ SHCHERBAKOV A A，TISHCHENKO A V.Light scattering in plane dielectric layers：modeling in the 2-D reciprocal space［J］.Journal of Quantitative Spectroscopy＆Radiative Transfer，2012，113（18）：2424-2430.

［5］ WUW，QIN Sh Q，HUANG Zh Q.A fast inversionmethod forwater droplet size determination in scattering lightmeasurement［J］.Journal of Optics，2011，31（7）：1-5（in Chinese）.

［6］ HUANG Zh Q，YANG JM，SUN Ch Sh.Application of the laser scattering theory for monitoring steam wetness and droplet size in steam turbines［J］.Journal of Power Engineering，2006，26（2）：241-244（in Chinese）.

［7］ CAIW W，ZHAO Y，MA L.Direct recursion of the ratio of Bessel functionswith applications to Mie scattering calculations［J］.Journal of Quantitative Spectroscopy＆Radiative Transfer，2008，109（16）：2673-2678.

［8］ HUANG Zh Q，QIN Sh Q.Investigation of exhaustwetnessmeasurementmethod in steam turbine based on mie scattering of laser［D］.Changsha：Graduate Schoolof National University of Defense Technology，2010：1-118（in Chinese）.

［9］ ZHANG H Y，ZHAOW J，REN D M，et al.Improved algorithm of Mie scattering parameter based on MATLAB［J］.Journal of Light Scattering，2008，20（2）：102-110（in Chinese）.

［10］ GODDEERIS C，CUPPO F，REYNAERS H，et al.Light scatteringmeasurementsonmicroemulsions：estimation ofdroplet sizes［J］.International Journal of Pharmaceutics，2006，312（1／2）：187-195.

［11］ HUANG Zh Q，CAO X L，YANG JM，et al.Application of CCD in measuring steam moisture and droplet size［J］.Opto-Electronic Engineering，2010，37（4）：39-43（in Chinese）.

Application of fast inversion algorithm in measurement of steam hum idity of steam turbine

LIU Fangyan1，HUANG Zhuqing1，2，CAO Xiaoling1，CAICheng1，YANG Ying1
（1.School of Energy and Power Engineering，Changsha University of Science＆Technology，Changsha 410114，China；2.Hunan Nonferrous Metals Vocational and Technical College，Zhuzhou 412006，China）

In order to solve the problem confronted with the online steam humiditymeasurementof turbine flow pass，a semi-empirical formula of phase function computingmethod was proposed to improve the inversion algorithm on scattering light distribution.Phase function of double Gaussian fitting by using MATLAB with cftool was adopted in this algorithm.The fitting result shows that the relative error is in small，and the approximate analytic solution of the Mie scattering theory could be got by the fitting function，which means that a rapid inversion from the scattering light intensity distribution to water quality radius.According to the results，with the restriction of the range of the droplet size，the approximation of the theory between the droplet size and scattering ratio was got.Contrast experiment showed themeasured scattering ratio was similar with the simulated scattering ratio.Based on the semi-empirical model，the water quality of middle radius was 1.1μm.Thefast inversion algorithm can well resolve the onlinemeasurement of steam humidity.

scattering；water qualitymiddle radius；double Gaussian fitting；turbine

O436.2

A

10.7510／jgjs.issn.1001-3806.2014.03.023

1001-3806（2014）03-0389-05

湖南省自然科学基金资助项目（12JJ2031）；湖南省科技厅重点资助项目（2011GK4005）

刘芳艳（1987-），女，硕士研究生，主要研究方向为光学测量中实验数据处理及分析。

*通讯联系人。E-mail：huangzhuqing＠aliyun.com

2013-05-27；

2013-06-21