框架墩式码头结构绕流数值模拟
2014-06-09吕启兵刘明维李鹏浩
吕启兵,杨 斌,刘明维,李鹏浩
(1.中交第二航务工程勘察设计院有限公司,湖北 武汉 430071;2.重庆交通大学 河海学院,重庆400074;3.温州港集团有限公司,浙江 温州 325100)
框架墩式码头结构绕流数值模拟
吕启兵1,杨 斌2,刘明维2,李鹏浩3
(1.中交第二航务工程勘察设计院有限公司,湖北 武汉 430071;2.重庆交通大学 河海学院,重庆400074;3.温州港集团有限公司,浙江 温州 325100)
基于FLUENT软件,针对不同方柱排列组合进行绕流数值模拟,得到不同间距比时各方柱水流阻力系数及三维流场情况,探寻框架墩式结构水流力分布规律。计算结果表明,简单的双方柱串、并联时,方柱阻力变化较有规律;双排并列三方柱绕流时,第一排方柱阻水作用显著,处于尖角位置的方柱绕流参数呈现对称现象,各方柱阻力明显增大,但阻力变化已无规律可循;当上下横撑间距为3倍横撑直径时,相互间影响已经较小;处于上游第一排横撑的水流阻力系数与单方柱时基本相同,第二排横撑所受水流阻力明显减小,与水流方向一致的纵撑其水流阻力可忽略不计。
码头;水流力;方柱;阻力系数;数值模拟
方柱绕流包含丰富的物理现象,如剪切层的转捩,流体与方柱壁面的分离,方柱上涡的周期性脱落,以及尾涡的形成与演变等,并广泛存在于各种工程实际中,研究方柱的绕流具有重要的工程实际意义与应用价值。
三峡水库蓄水发电以后,库区水位发生巨大变化,在库区河段季节性暴雨等极端天气情况下,三峡水库上游码头将经受高水位、大流速的特殊水文条件考验,水流作用势必会对码头产生重要影响。以方柱为主要结构型式的框架墩式码头,自身设有多层横纵联系撑,方柱结构体型间相互作用,结构受水流影响复杂,多层连续排架码头结构所受水流荷载目前仍无法准确计算。
目前,圆柱组合绕流模拟的研究较多[1-3],方柱组合绕流在此类实际工程中研究相对较少。A.Agrawal等[4]运用LBM算法对并列双方柱绕流进行模拟,研究了间距比分别为0.7与2.5情况下双方柱柱后尾流结构特性;唐浩俊等[5]做了串列方形双塔的风荷载及间距比的影响研究,得到间距比为3时,两柱阻力之和最小,大于3时,可忽略下游柱对上游柱产生的干扰;陈素琴等[6]采用改进的标志网格(MAC)方法,对不同间距下两串列方柱的气动力及相互干扰特性进行了模拟,计算结果表明,当达到临界间距时,两串列方柱的阻力系数不再随间距比的变化而改变。饶勇等[7]对不同间距下并列双方柱进行绕流数值模拟,得到相应流线图、方柱升力图及阻力图,并对其进行了分析探讨。综上所述,简单排列的方柱绕流数值模拟研究不少,但较复杂排列的二维三维数值模拟研究并不多见。
为准确了解框架墩式码头结构所受水流力问题,探究码头排架结构所受水流荷载规律,本文模拟不同方柱排列情况下的相互影响关系,探究此类码头水流荷载计算问题,对码头结构更加明确的受力分析、结构优化以及降低工程造价等方面有着重大的实际意义。
本文基于FLUENT流体计算软件,参照某内河框架墩式码头结构型式,建立二维与三维计算模型,逐步从简单的两方柱绕流和多方柱绕流,再到带横纵联系撑的三维方柱绕流模拟。
1 数值模型与计算验证
1.1 控制方程
对于不可压缩黏性流体,在直角坐标系下,流体的运动可用Navier-Stokes方程[8]与动量方程描述:

模拟计算采用RNG k-ε模型,该模型是由Yakhot和Orzag提出,模型是从瞬态N-S方程中推出的,通过大尺度运动和修正后的黏度项体现小尺度的影响,而使这些小尺度运动有系统地从控制方程中去除,所得到的k方程和ε方程与标准k-ε模型非常相似:
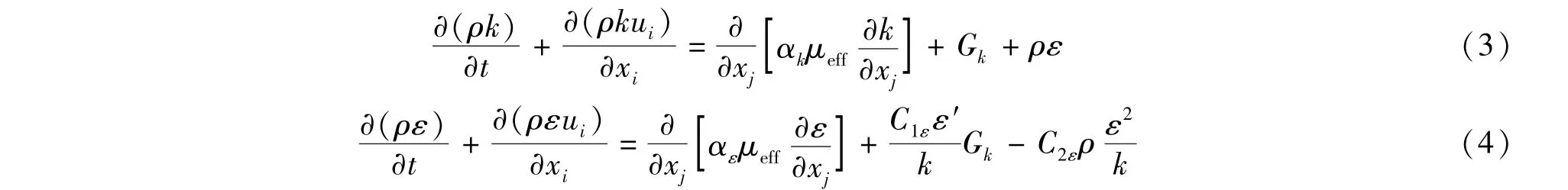
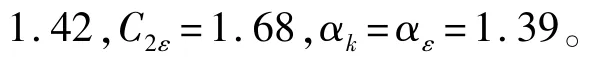
RNG k-ε模型来源于严格的统计技术,是对标准k-ε模型的重要改进。RNG模型在ε方程中加入了一个Rε条件,从而反映了主流的时均应变率Eij,这样该模型中的产生项不仅与流动情况有关,而且在同一问题中仍然是空间坐标的函数,从而可以更好地处理高应变率及流线弯曲程度较大的流动[9]。
1.2 二维及三维计算模型
依据框架墩式码头的桩柱排列形式,设定不同排列形式下方柱的间距比,串联双方柱时L/D (D为方柱边长)=1,2,3,4;并列双方柱时L/D= 2,2.5,3;并列三方柱时L/D=1,2,3,4,双排并列三方柱时L/D=1.5,2,2.5,3,L′/D=2,2.5,3,如图1所示。
图2为三维单横撑、双横撑以及横纵撑模型设置,考虑工程实际,上下横撑间距设置为3d(d为横撑直径)。

图1 二维方柱绕流布置Fig.1 Arrangement of two dimensional flow around square column

图2 三维带横撑方柱绕流布置Fig.2 Arrangement of square column flowing around three-dimensional cross section
1.3 数值算法
二维计算区域网格经对比试算采用非结构化网格,三维网格运用size function减少网格数。方柱周围流动较复杂,应适当网格加密。利用有限体积法(FVM)对方程进行离散,选择压力基求解器与压力二阶离散格式,动量、湍动能和湍动耗散率选项全部为二阶迎风格式,计算选用RNG k-ε模型、PISO算法,计算过程中残差精度设定为10-5[10]。
1.4 边界条件
考虑工程实际及水流雷诺数,计算中取边界进口流速U=1 m/s,出口为自由出流,方柱表面为壁面的无滑移边界条件。方柱边长D=1.5 m,二维方柱距入口边界10D,上下边界与方柱距离10D,与出口距离15D。三维模型布置与二维模型基本相同,在保证计算精度与耗时前提下,三维模型进行了一定调整。三维情况时长方体流域除进口、出口与二维基本相同外,其余边界设置为对称边界,横撑直径d=0.8D=1.2 m。由于方柱在Re>1 000时水流阻力系数变化较小[11],并且考虑内河水流条件、计算机能力以及方柱绕流对雷诺数的敏感程度等因素,本文设定Re=UD/υ=22 000[12](U为来流流速,D为方柱边长,υ为流体运动黏度,取0.681 8×10-6m2/s)。
1.5 模型验算
验算以单方柱绕流的3个重要参数与相关文献对比分析。表1给出了本模型验证成果与其他相关数值模拟、模型试验结果的对比。各参数定义如下:Cd=Fd/(0.5ρu2D),Cl=Fl/(0.5ρu2D),St=fD/u,其中:Fd为绕流阻力;Fl为绕流升力;u为来流流速;D为方柱边长;f为涡街脱落频率,即方柱上涡街的脱落频率。本文中Cd为平均阻力系数,Cl为升力的最大值。单方柱结构化网格划分如图3所示。
从表1可以看出,本文模拟计算Re=22 000时,单方柱绕流的平均阻力系数基本约2.08,升力系数约1.34,斯特劳哈数St基本保持0.135不变,与Luo等模拟计算结果基本接近,且计算结果在Lyn试验的范围内;图4为验证模拟计算升、阻力系数曲线,模拟曲线较好符合单方柱绕流特征。验证表明,本计算模型能较好地模拟方柱的绕流及水力特性,分析方法用于实际码头方柱绕流阻力具有可靠性。

表1 单方柱绕流模拟计算结果比较Tab.1 Comparison between simulated results of flow around a single square column

图3 方柱结构化网格划分Fig.3 Structured grid division on a single square column
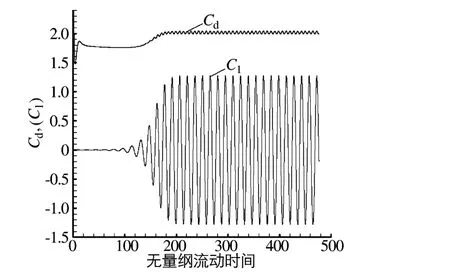
图4 单方柱的升、阻力系数曲线Fig.4 Lift and drag coefficients of a single square column
2 二维方柱绕流计算成果分析
2.1 串并列方柱的绕流
计算得到各方柱阻力系数见表2。结果显示,串联双方柱时上游方柱对下游方柱遮流影响明显,上游方柱的阻力基本保持不变,下游方柱的阻力在间距较小时甚至会出现负值的情况(L/D>2时,下游方柱阻力才出现正值)。两方柱并列时,各算例方柱的阻力系数基本相同,但随着间距的增大而逐渐减小。并列三方柱的水流阻力大于并列双方柱时的情况,表明其阻水作用较并列双方柱时有所增大。
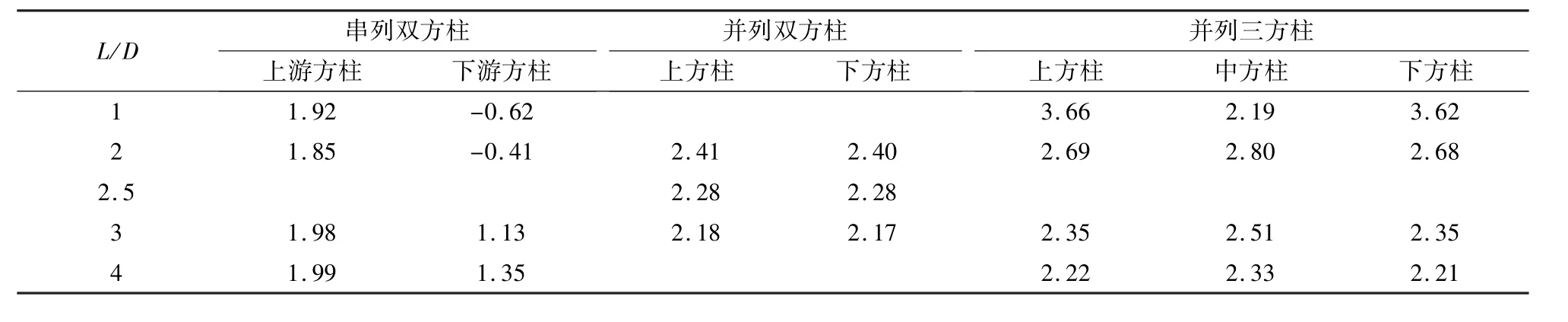
表2 串并列双方柱与并列三方柱阻力系数Tab.2 Drag coefficients of two square columns in series arranged side by side and three square columns side by side

图5 二维阻力系数Fig.5 Two-dimensional drag coefficient
图5为二维串并列时的阻力系数,串联时,间距的增大对上游方柱水流力几乎无影响,下游方柱水流力逐渐变大,遮流影响效果逐渐减弱;并列时,横向影响作用随间距的增加而减小,均趋于单柱时的情形。
2.2 双排并列三方柱的绕流
双排并列三方柱绕流计算结果见表3。此时各方柱的阻力系数较简单串并列时有一定的增大,尤其是上游第一排处于尖角位置的a方柱与e方柱,在L/D=1.5或2时,出现了阻力系数大于3的情况,所受水流阻力明显增大。
由于方柱前后的遮流影响存在,简单串、并联的遮流影响规律在此已不再适用。在L′/D=2时并没有出现下游方柱水流阻力为负值的情况,且甚至出现前方柱阻力小于后方柱阻力的情形,如表3中L/D=2.5的c,d方柱与L/D=3时的a,b与e,f方柱。但在间距较小(如: L/D=1.5与L/D=2)时,遮流影响仍比较明显。从表中可以看出:a,b与e,f方柱的数据基本呈对称现象,中间c方柱的阻力相对边柱有一定减小,其下游的d方柱阻力系数在L′/D=2与L′/D=2.5时变化并不大,只是在L′/D=3有小幅减小。
数据显示,随着横向间距的增加,前排三方柱的阻力值趋于接近,但对于下游并列的b,d与f方柱,其阻力与间距的变化并不一致,已较难观测其变化规律。
由图6可见,随着纵向间距的增加,处于上游尖角位置的a与e方柱阻力系数出现一定的增大,与串联两方柱绕流时上游方柱阻力几乎无变化有一定区别。纵向间距不变时,横向间距的增加,在纵向2D图中各阻力系数变化无明显规律,在纵向2.5D与3D图中仍有一定各方柱的水流阻力仍表现出随间距的增大而减小的趋势。可以发现,间距仍然是引起多方柱绕流前后压差变化导致方柱水流力改变的主要因素。

图6 双排并列三方柱纵向阻力系数Fig.6 Lengthways drag coefficient of three square columns of two lines and side by side
总体来说,由于双排并列三方柱的绕流已表现出群桩阻水的现象,与简单串、并排列情形相比已显得较为复杂,水流阻力并没有明显的规律可循,尤其是下游的方柱,其水流力在流经上游方柱水流的相互作用下已很难确定。

表3 双排并列三方柱阻力系数计算结果Tab.3 Drag coefficient calculation results of three square columns of two lines and side by side
3 三维方柱绕流计算结果及分析
3.1 单横撑的绕流
图7给出了单横撑时横撑的水流阻力系数监测曲线,其值基本在2.0附近波动,此时与横撑相连的方柱水流阻力系数与二维同等间距下的计算结果一致,仍为2.4。
图8为单横撑时的流线图与压力云图,压力较大面为迎水面,柱体后方的背水面压力较小,与实际情况相符。从流线图中可以看出,由于方柱间横撑的存在,在横撑后方水流流线显得较为杂乱无序,并形成一定的回流区,与二维计算时的流线图有较大区别,水流流动的三维特性明显。
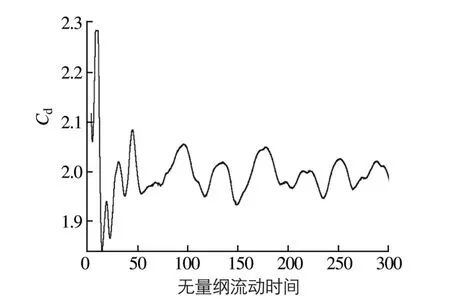
图7 单横撑的水流阻力系数Fig.7 Drag coefficient of a single cross

图8 流线图与压力云图(单位:Pa)Fig.8 Streamline chart and stress nephogram(unit:Pa)
3.2 双横撑的绕流
图9为双横撑时上下横撑的水流阻力系数监测曲线,由图可见,两条曲线非常接近,上下横撑的水流阻力系数都基本在2.0左右,与单横撑时的水流阻力系数基本相同,表明一般实际工程中上下横撑间距为3d及以上时,相互间影响已经较小,此时横撑的水流阻力可按2.0的水流阻力系数进行计算。
图10为双横撑流线图与压力云图,方柱后方水流流态更加紊乱,水流经方柱后流动更为复杂,影响程度较单横撑时明显加强。图11为双横撑时的x方向速度云图,模型的顶层面与底层面流速分布与二维并列双方柱绕流时的流速分布基本相似,逐渐靠近横撑时的流速分布改变越明显,由于横撑的阻挡作用,横撑后方明显存在两个流动较弱的空间区域。

图9 上下横撑阻力系数变化Fig.9 Drag coefficient of up and down crosses

图10 流线图与压力云图Fig.10 Streamline chart and stress nephogram

图11 x方向流速截面云图(单位:m/s)Fig.11 Velocity section contours of x direction(unit:m/s)
3.3 单层横纵撑的绕流
图12为单层横纵撑时下游横撑的水流阻力系数监测曲线图,从图中显示,由于上游横撑与方柱的存在,下游横撑的水流阻力系数已经明显减小,其阻力系数稳定后基本维持在0.5左右;纵撑的阻力系数计算得到约为0.009,因此,在计算码头水流力荷载时,几乎可不考虑沿水流方向的纵撑水流力。图13为单层横纵撑的流线图与压力云图,此时水流通过构筑物时流线已杂乱无章,尤其是在联系撑的周围;方柱后方水流回流明显。图14为各方向速度截图。图中x方向截面图显示,构筑物后方仍然存在流速减小区域,y方向截面图反映出方柱侧后方流速与流速分布区间均较大(可达约1.5 m/s),与二维较为相似,z方向截面图显示横撑上下面的流速较大,流经第一排横撑后流速明显减小,流经第二排横撑流速进一步减小,甚至出现负值(-0.6 m/s)的流速,此时构筑物外围流场情况与二维模拟时同样基本类似。

图12 下游横撑绕流阻力系数变化Fig.12 Drag coefficient of downstream cross
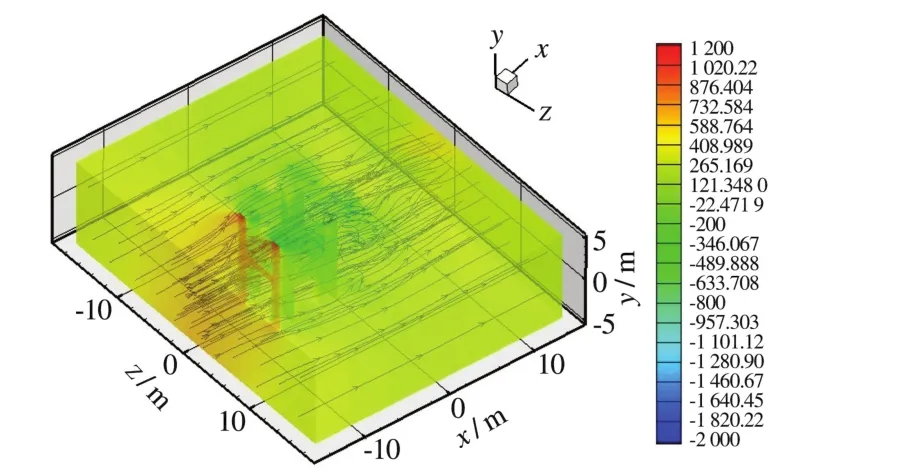
图13 流线图与压力云图(单位:Pa)Fig.13 Streamline chart and stress nephogram(unit:Pa)

图14 各方向流速截面图(单位:m/s)Fig.14 Velocity section drawing of three directions(unit:m/s)
4 结 语
本文基于FLUENT软件,针对不同方柱排列组合进行绕流数值模拟,得到二维串并联两方柱、单排与双排并列三方柱以及三维带单、双层横撑与单层横纵撑相关构筑物的阻力系数,并得到相应流场的情况。主要结论如下:
(1)与简单排列的方柱绕流对比发现,多方柱情形时,相互影响已非常复杂,简单地只考虑遮流与横向影响计算水流力已显不足。
(2)库区环境下方柱间距仍是影响其水流力的主要因素,间距的变化对其水流力影响较大,多方柱串并联时的方柱水流力已较难预测。
(3)在不考虑贴岸条件情况下,类似水流条件的码头水流力计算可参考表3。对于上游第一排横撑水流阻力系数可按2.0考虑,其下游第二排横撑阻力系数减小到0.5左右,码头中纵撑的水流力可不予考虑。
(4)三维模拟时尾流的三维特性明显。方柱侧方或侧后方水流流速均变化较大,横撑后方均存在回流空间区域,尾流对下游柱的干扰作用显著。
[1]刘松,符松.串列双圆柱绕流问题的数值模拟[J].计算力学学报,2000,17(3):260-266.(LIU Song,FU Song. Numerical simulation of flow past two cylinder in tandem arrangement[J].Chinese Journal of Computational Mechanics,2000, 17(3):260-266.(in Chinese))
[2]楼小峰,曹丰产,林志兴.串列钝体绕流的数值计算[J].同济大学学报,2002,30(5):604-608.(LOU Xiao-feng,CAO Feng-chan,LIN Zhi-xing.Numerical simulation of flows around two bluff bodies in tandem arrangement[J].Journal of Tongji University,2002,30(5):604-608.(in Chinese))
[3]HUERA-HUARTE F J,BRARMAN P W.DPIV in the wake of a tandem arrangement of two flexible circular cylinders[J]. Journal of Visualization,2010,13(3):195-202.
[4]AGRAWAL A,DJENIDI L,ANTONIA R A.Investigation of flow around a pair of side-by-side square cylinders using the lattice Boltzmann method[J].Computers&Fluids,2006,35:1093-1107.
[5]唐浩俊,李永乐,胡朋.串列双塔柱凤荷载及涡振性能研究[J].工程力学,2013,30(1):378-383.(TANG Hao-jun,LI Yong-le,HU Peng.Wind loads and vortex-induced vibration of two tower columns in tandem arrangement[J].Engineering Mechanics,2013,30(1):378-383.(in Chinese))
[6]陈素琴,黄自萍,沈剑华,等.两串列方柱绕流的干扰数值研究[J].同济大学学报:自然科学版,2001,29(3):320-325.(CHEN Su-qing,HUANG Zi-ping,SHEN Jian-hua,et al.Numerical computation of the flow around two square cylinders in tandem arrangement[J].Journal of Tongji University(Natural Science),2001,29(3):320-325.(in Chinese))
[7]饶勇,倪玉山,刘超峰.并列双方柱绕流的Lattice Boltzmann模拟分析[J].应用力学学报,2008,25(2):192-197. (RAO Yong,NI Yu-shan,LIU Chao-feng.Lattice Boltzmann simulation of flow round two square cylinders arranged side by side [J].Chinese Journal of Applied Mechanics,2008,25(2):192-197.(in Chinese))
[8]张远君.流体力学大全[M].王平,译.北京:北京航空航天大学出版社,1991.(ZHANG Yuan-jun.Fluid mechanics [M].Translated by WANG Ping.Beijing:Beihang University Press,1991.(in Chinese))
[9]王福军.计算流体动力学分析-CFD软件原理与应用[M].北京:清华大学出版社,2004.(WANG Fu-jun.Computational fluid dynamics analysis-CFD software principle and application[M].Beijing:Tsinghua University Press,2004.(in Chinese))
[10]谢志刚,许春晓,崔桂香,等.方柱绕流大涡模拟[J].计算物理,2007,24(2):171-180.(XIE Zhi-gang,XU Chunxiao,CUI Gui-xiang,et al.Numerical large eddy simulation of flow around square cylinder[J].Chinese Journal of Computational Physics,2007,24(2):171-180.(in Chinese))
[11]毕继红,余化军,任洪鹏.静止方柱和圆柱绕流的二维数值分析[J].三峡大学学报:自然科学版,2012,34(1):41-45.(BI Ji-hong,YU Hua-jun,REN Hong-peng.Two dimensional numerical simulation of flow over a static square cylinder and a static circular cylinder[J].Journal of China Three Gorges University(Natural Sciences),2012,34(1):41-45.(in Chinese))
[12]王远成,吴文权.基于RNG湍流模型钝体绕流的数值模拟[J].上海理工大学学报,2004,26(6):519-523.(WANG Yuan-cheng,WU Wen-quan.Numerical simulation of flow around blunt bodies using RNG turbulence model[J].Journal of University of Shanghai for Science and Technology,2004,26(6):519-523.(in Chinese))
[13]LUO S C,YAZDANI M G,CHEW Y T,et al.Effects of incidence and afterbody shape on flow past bluff cylinders[J].Journal of Wind Engineering and Industrial Aerodynamics,1994,53(3):375-399.
[14]VIKERY B J.Fluctuating lift and drag on a long cylinder of square across section in a smooth and in a turbulent stream[J]. Journal of Fluid Mechanics,1966,25(3):481-494.
[15]YU D,KAREEM A.Numerical simulation of flow around rectangular prism[J].Journal of Wind Engineering and Industrial Aerodynamics,1997(67/68):195-208.
[16]张伟,葛耀君.不方柱绕流粒子图像测速试验与数值模拟[J].同济大学学报:自然科学版,2009,37(7):858-861. (ZHANG Wei,GE Yao-jun.Particle image velocimetry study and numerical simulation of turbulent near wake of square cylinder[J].Journal of Tongji University(Natural Science),2009,37(7):858-861.(in Chinese))
[17]LYN D A,EINAV S,RODI W,et al.A laser-Doppler velocimetry study of ensemble-averaged characteristics of the turbulent near wake of a square cylinder[J].Journal of Fluid Mechanics,1995(304):285-319.
Numerical simulation of flow around frame dolphin pier structure
LV Qi-bing1,YANG Bin2,LIU Ming-wei2,LI Peng-hao3
(1.CCCC Second Harbor Consultants Co.,Ltd.,Wuhan 430071,China;2.School of River&Ocean Engineering,Chongqing Jiaotong University,Chongqing 400074,China;3.Wenzhou Port Group Co.,Ltd., Wenzhou 325100,China)
Based on the FLUENT software,different permutations and combinations of square cylinders are used to simulate the flow around frame dolphin pier structure,and get the resistance coefficients and the three dimensional flow field of each square column with different spacing ratios,and explore the law of the flow force distribution on the structure.The calculation results show that the square column resistance changes regularly in series and tied for simply two columns.When two rows of three square columns are used,the first row of the square columns blocks the water remarkably.The parameters of the flow around the square columns in the sharp corners position are symmetric,the resistance of each square column increases obviously,but haphazard.When the fluctuation cross arm spacing is 3 d,it has a little effect on each other.The resistance coefficient of lateral cross arm is basically the same in the first row at the upstream,and the flow resistance of lateral cross arm of the second row decreases obviously.The flow resistance of the vertical support can be neglected.The flow resistance of the vertical cross arm can be ignored with the flow in the same direction.
wharf;flow force;square column;drag coefficient;numerical simulation
TV135.6;U656.1+22
A
1009-640X(2014)06-0022-08
2014-05-20
“十二五”国家科技支撑计划资助项目(2012BAB05B00)
吕启兵(1986-),男,重庆人,硕士研究生,主要从事港口海岸工程结构与基础方面的研究。E-mail:lvqb1986@163.com
