抑制式模糊C－均值聚类研究综述

范九伦

（西安邮电大学 通信与信息工程学院，陕西 西安710121）

计算机技术和网络技术的飞速发展，使得人们面对的数据类型越来越多，数据维数越来越高，数据量越来越大，目前世界已进入大数据时代。大数据时代对人类的数据驾驭能力提出了新的挑战，也为人们获得更为深刻、全面的洞察能力提供了前所未有的空间与潜力。作为数据分析的基本工具，模式识别的内涵在不断的扩大，模式识别的方法在不断的推新。鉴于现实的数据很多是没办法事先进行分类的，因此无监督模式识别方法越来越受到重视，而聚类分析是无监督模式识别的主要方式，因此国际上对聚类分析的理论、方法、算法的研究一直没有间断，这些年大有上涨趋势，各种有关聚类分析及应用的文章和著作层出不穷。

在众多的聚类算法中，经典的硬C－均值（HCM）聚类算法是一个被人们经常使用的著名算法，其显著优点是原理简单直观、运行速度快，其明显缺点是数据的“硬划分”导致数据的分类不够理想。鉴于此，早在上世纪七八十年代，人们就开始考虑将数据的“硬划分”改为“软划分”（即：模糊划分），从而提出了著名的并被经常使用的模糊C－均值（FCM）聚类算法［1－3］。由于隶属函数的引入，使得目标函数可表示的内容更为宽泛，这使得模糊聚类不仅能够处理团状数据，也能够处理线状数据、面状数据、壳状数据等众多的数据类型。此外，人们也对模糊聚类的各种拓展进行了研究，如可能性聚类、可能性－模糊混合聚类、模糊C－均值聚类的各种广义表达形式［4－9］。

FCM聚类相比HCM聚类的视野更为宽泛、内容更为丰富，但FCM聚类的一个不容忽视的缺点是运行速度远比HCM聚类慢得多，使其应用于大数据分析面临诸多困难。为了提高FCM聚类的运行速度，研究者们也做了各种各样的努力，但均没有明显的受益。鉴于一个好的聚类算法应该对现实应用系统中经常出现的大数据有好的分类性能，为了给出一种能体现HCM聚类和FCM聚类各自优点且分类性能良好的算法，我们提出了抑制式模糊C－均值（S－FCM）聚类算法［10］，该算法在数据分类时引入“抑制式竞争学习”机制，通过对每个样本的最大隶属度进行奖励的同时抑制其它隶属度的方式，在运行速度和分类性能两个方面均比FCM聚类算法有显著提高。该算法的另一个优点是将HCM聚类和FCM聚类融为一体，通过抑制率α（0≤α≤1）的不同取值可分别得到 HCM 聚类和FCM聚类，即α＝0时为 HCM 聚类；α＝1时为FCM 聚类，0＜α＜1为S－FCM聚类。

1 S－FCM聚类算法

对于ℝq空间上的数据集X＝｛x1，x2，…，xn｝，通过聚类将数据划分成c个类，每类的样本中心记为vi（i＝1，2，…，c），uij表示样本xj到第i个类vi的隶属度，d2ij＝‖xj－vi‖2表示样本xj到第i个类vi的距离，m表示模糊C－均值聚类算法中的模糊因子，通常取为2。

模糊聚类问题可表述为数学规划

使得

这里U＝｛uij｝是一个c×n矩阵，V＝［v1，v2，…，vc］是一个q×c矩阵。该数学规划问题可如下求解［1］。

初始化 初始中心V（0），令k＝0，选择ε＞0。

步骤1 用（2a）和（2b）计算U（k）。

如果 ∀j，r，dij（k）＞0，那么

如果存在j，r使得dij（k）＝0，那么令

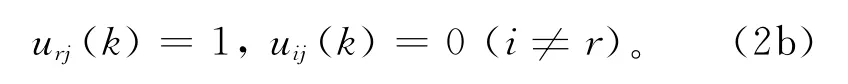
步骤2 用（2c）计算V（k＋1）。

步骤3 如果 ‖V（k）－V（k＋1）‖ ＜ε，停止；否则令k＝k＋1回到步骤1。

上述算法也可用U（0）作为初始化。这里要求m≥1，当m＝1时上述算法退化为HCM聚类算法。

FCM聚类算法具有很好的适应性，但运行速度难以满足现实需求。另外，模糊因子m的选择对算法性能有一定影响。鉴于此，我们基于“竞争学习机制”的思想，提出了抑制式模糊C－均值（S－FCM）聚类算法［10］，具体如下。

在步骤2之前插入一个对uij的修改过程。

步骤1＊对每一个样本xj，记

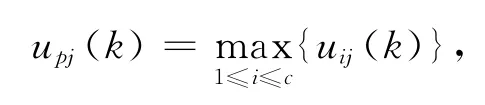
那么

这里0≤α≤1是一个抑制因子，用于控制抑制的程度。上述修改算法称为抑制式模糊C－均值（SFCM）聚类算法。可以看到，当α＝0时S－FCM变为HCM聚类；α＝1时S－FCM变为FCM聚类。抑制率α的引入，从另一个途径建立起FCM和HCM之间的桥梁。大量的实例表明，S－FCM的分类性能优于FCM。

S－FCM聚类算法的思想非常简单。模糊聚类的目的是为了分类，在计算过程中获得的隶属度，已经显现出样本的分类趋势。自然的我们希望隶属度越大的样本拥有竞争优势，对最终分类的话语权越大。当xj到某一个类中心的隶属度具有竞争优势时，应该对这种竞争态势予以奖励。换句话说，应该对该样本到其它类的隶属度值进行抑制，抑制的程度取决于抑制率α，而把抑制的累加值奖励给竞争中的获胜者。

2 S－FCM聚类算法研究现状

自从S－FCM聚类算法提出后，国际上很多学者对该算法给予关注，如罗马尼亚学者、匈牙利学者、土耳其学者、印度学者、台湾学者、韩国学者、以色列学者、孟加拉国学者、澳大利亚学者、英国学者、我国学者。国际上很多学者也对该算法本身及其应用进行了深入研究。

针对S－FCM聚类，目前的研究大致上可分为以下6个部分。

（1）S－FCM 聚类算法的理论分析

有关S－FCM 聚类算法的理论问题包括：SFCM聚类算法的竞争学习机理是什么？S－FCM聚类算法是否收敛？

罗马尼亚和匈牙利学者们从理论的角度研究了S－FCM 聚类算法［11－18］，尤其是LászlóSzilágyi专门以S－FCM聚类算法为主要研究内容完成了博士论文（L.Szilágyi，Novel image processing methods based on fuzzy logic，PhD Thesis，BUTE Budapest，2008）［18］。

为了分析S－FCM聚类算法的竞争学习行为，LászlóSzilágyi等人分析了抑制率α的作用，通过引入Quasi Learning Rate（QLR）来定性分析抑制效果，得到非获胜者的抑制率在数学上等价于获胜者与给定的样本之间距离的“虚拟”缩短。其结论是S－FCM聚类算法具有伪竞争性。

为了分析S－FCM 聚类算法的收敛性，László Szilágyi等人提出了S－FCM聚类算法的优化版本Optimally Suppressed FCM（OS－FCM）并给出可收敛的迭代算法，通过分析计算和数值模拟表明这两个算法的性能基本相当，这从另一个侧面表明SFCM聚类算法具有收敛行为，尽管从理论上目前还没有好的办法证明其收敛性。

（2）抑制率α的固定选择

在算法运行前经验选择一个固定的α值，该值与迭代次数无关。抑制率α的固定选择是在原始SFCM中提出的，作为一种折中，建议取α＝0.5以便既保持FCM优良的分类性能又体现HCM运行速度快的优点。实验结果表明，S－FCM 在不降低FCM分类性能的同时运行速度有明显提高。此外，S－FCM对模糊因子m不太敏感。

（3）抑制率α的不固定选择

即抑制率α是变化的，换句话说抑制率是迭代次数的函数。这一思路改变了原始S－FCM的初衷，其目的不在于提高速度而是更多的关注更加优越的分类性能。

国际模糊工程领域著名专家、台湾中原大学杨敏生教授及其学生们对抑制率α的确定进行了深刻研究，他们基于原型驱动学习的思想给出抑制率α的指数型选择公式［19］和相应的算法 MS－FCM，通过在核磁共振成像（MRI）图像上的大量实验指出“MS－FCM clustering algorithm is more efficient and is strongly recommended as an MRI segmentation technique”。此外，人们还提出了一些抑制率α的其它选择方法，如台湾学者［20］给出柯西型选择公式、韩国学者［21］给出含有模糊因子m的指数型选择公式、国内学者［22］给出采用模糊偏差的指数型选择公式、孟加拉国学者［23］引入清晰度来选取更为细致的抑制率。

（4）在核聚类算法中引入抑制式思想

台湾中原大学杨敏生教授及其学生们在其提出的核聚类算法中嵌入了抑制式竞争学习机制，并将其应用于MRI图像的分割，获得了满意的效果［24－26］。

除此之外我国学者［27－28］、孟加拉国学者 M.A.Ali及其澳大利亚和英国合作者也对S－FCM聚类算法进行了相关探讨［29－30］。

（5）将抑制式思想应用于相关领域

如抑制式竞争学习机制应用于聚类神经网络［31－33］，抑制式竞争学习机制应用于学习矢量量化［34］，抑制式竞争学习机制应用于支持矢量机［35］，抑制式竞争学习机制应用于粗糙－模糊聚类［36－37］。

（6）用抑制式思想解释已有算法

S.Krinidis和 V.Chatzis于2010年提出了FLICM算法［38］，最近LászlóSzilágyi［39］分 析了FLICM算法的理论基础及其存在的错误，并用SFCM的思想解释了该算法的细节处理过程，以进一步修正错误明辨是非。

经过近10年的研究，S－FCM聚类算法所体现的抑制式竞争学习机制的思想逐渐得到国内外研究者们的普遍认可。正如孟加拉国学者 M.A.Ali及其澳大利亚和英国合作者在其综述文章中所评价的［40］，抑制式模糊C－均值聚类算法已成为与模糊C－均值聚类算法、可能性C－均值聚类算法一样的很受欢迎和广泛使用的模糊聚类算法。印度学者R.Ravindraiah和K.Tejaswini在其综述文章中也建议采用抑制式竞争学习机制来加速相关模糊聚类算法［41］。

3 后期研究的一些建议

尽管对S－FCM的研究已经取得了一些成果，但仍有很多问题值得进一步探讨，下面列举几个问题供大家研究时参考。

（1）抑制率α的固定选择问题。如何根据数据结构选择合适的α值，目前还没有进一步的报道。

（2）抑制率α的不固定选择问题。目前已经有一些抑制率α随迭代次数变化的选择办法，但这些办法并非惟一的办法，仍可给出一些其它选择途径。

（3）在相关学习算法中嵌入抑制式竞争学习机制。前述的一些学习算法已经嵌入了抑制式竞争学习思想并获得成功，这为进一步在很多学习算法中嵌入抑制式思想提供了借鉴依据，这方面仍有很多工作可做。

（4）依据伪学习率的广义抑制式模糊C－均值聚类算法。最近，通过改变伪学习率而非直接选择抑制率的方式，L.Szilágyi和S.M.Szilágyi提出了一系列广义形式的抑制式模糊C－均值聚类算法［17］，这为深入探讨开辟了新的途径，这方面的研究刚刚开始，可做的工作还很多。

［1］Bezdek J C.Pattern Recognition with fuzzy objective function algorithms ［M］.New York： Plenum Press，1981.

［2］Bezdek J C，Keller J，Krishnapuram R，et al.Fuzzy models and algorithms for pattern recognition and image processing［M］.New York：Springer，1999.

［3］Yang M S.A survey of fuzzy clustering［J］.Math Comput Model，1993，18：1－16.

［4］Krishnapuram R，Keller J.A possibilistic approach to clustering［J］.IEEE Trans Fuzzy Syst，1993，1（2）：98－110.

［5］Pal N R，Pal K，Keller J M，et al.A possibilistic fuzzy c－means clustering algorithm［J］.IEEE Trans Fuzzy Systems，2005，13（4）：517－530.

［6］Yu J，Yang M S.Optimality test for generalized FCM and its application to parameter selection［J］.IEEE Trans Fuzzy Systems，2005，13（1）：164－176.

［7］Jian Yu，General C－means clustering model［J］.IEEE Trans PAMI，2005，27（8）：1197－1211.

［8］Yang Z，Chung F－L，Wang S.Robust fuzzy clustering－based image segmentation［J］.Applied Soft Computing，2009，9：80－84.

［9］Zhu L，Chung F－L，Wang S.Generalized fuzzy C－means clustering algorithm with improved fuzzy partitions［J］.IEEE Trans.SMC－PartB，2009，9（3）：578－591.

［10］Fan J L，Zhen W Z，Xie W X.Suppressed fuzzy C－means clustering algorithm［J］.Pattern Recognition Letters，2003，24（9／10）：1607－1612.

［11］Szilágyi L，Szilágyi S M，Benyo Z.A thorough analysis of the suppressed fuzzy C－means algorithm［J］.Progress in Pattern Recognition，Image Analysis and Applications，Lecture Notes in Computer Science，2008，5197：203－210.

［12］Szilágyi L，Szilágyi S M，Benyo Z.Analytical and numerical evaluation of the suppressed fuzzy c－means algorithm［J］.Lecture Notes in Computer Science，2008，5285：146－157.

［13］Szilágyi L，Szilágyi S M，Benyo Z.A unified approach to c－means clustering models［C］／／IEEE International Conference on Fuzzy Systems，2009：456－461.

［14］Szilágyi L，Iclanzan D，Szilágyi S M，et al.A generalized C－means clustering model using optimized via evolutionary computation［C］／／IEEE International Conference on Fuzzy Systems，2009：451－455.

［15］Szilágyi L，Szilágyi S M，Kiss C.A generalized approach to the suppressed fuzzy c－means algorithm［J］.Modeling Decisions for Artificial Intelligence，Lecture Notes in Computer Science，2010，6408：140－151.

［16］Szilágyi L，Szilágyi S M，Benyo Z.Analytical and numerical evaluation of the suppressed fuzzy c－means algorithm：a study on the competition in c－means clustering models［J］.Soft Comput，2010，14：495－505.

［17］Szilágyi L，Szilágyi S M.Generalization rules for the suppressed fuzzy c－means clustering algorithm［J／OL］.Neurocomputing.（2014－04－13）［2014－04－26］.http：／／www.sciencedirect.com／science／article／pii／S0925231214004263.

［18］Szilágyi L.Novel image processing methods based on fuzzy logic［D］.BUTE Budapest，2008.

［19］Hung W L，Yang M S，Chen D H.Parameter selec－tion for suppressed fuzzy C－means with an application to MRI segmentation［J］.Pattern Recognition Letters，2006，27：424－438.

［20］Hung W L，Chang Y C.A modified fuzzy C－means algorithm for differentiation in MRI of ophthalmology［J］.Modeling Decisions for Artificial Intelligence，Lecture Notes in Computer Science，2006，3885：340－350.

［21］Nyma A，Kang M，Kwon Y－K，et al.A hybrid technique for medical image segmentation［J］.Journal of Biomedicine and Biotechnology，2012E－location.DOI：10.1155／2012／830252.

［22］Li Y，Li G.Fast fuzzy c－means clustering algorithm with spatial constraints for image segmentation［J］.Advances in Neural Network Research and Applications，Lecture Notes in Electrical Engineering，2010，67：431－438.

［23］Saad M F，Alimi A M.Improved modified suppressed fuzzy C－means［C］／／2nd International Conference on Image Processing Theory，Tools and Applications（IPTA），2010：313－318.

［24］Hung W L，Yang M S，Chen D H.Segmentation in MRI of ophthalmology using a robust－type clustering algorithm ［C］／／IEEE International Conference on Fuzzy Systems，2009：427－430.

［25］Hung W L，Yang M S，Chen D H.Color image segmentation using cauchy－type fuzzy c－means algorithm［C］／／Fourth International Conference on Fuzzy Systems and Knowledge Discovery，2007：24－27.

［26］Tsai H S，Hung W L，Yang M S.A robust kernelbased fuzzy C－means algorithm by incorporating suppressed and magnified membership for MRI image segmentation［J］.Artificial Intelligence and Computational Intelligence，Lecture Notes in Computer Science，2012，7530：744－754.

［27］黄建军，谢维信.半抑制式模糊C－均值聚类算法［J］.中国体视学与图像分析，2004，9（2）：109－113.

［28］Zhao F，Fan J L，Liu H Q.Optimal－selection－based suppressed fuzzy c－means clustering algorithm with self－tuning non local spatial information for image segmentation［J］.Expert Systems with Applications，2014，41（9）：4083－4093.

［29］Ali M A.Karmakar G C，Dooley L S.Fuzzy image segmentation using suppressed fuzzy C－means clustering（SFCM）［C］／／International Conference on Computer and Information Technology（ICCIT 04），2004：363－368.

［30］Ali M A.Laurence S D，Gour C K.Automatic feature set selection for merging image segmentation results using fuzzy clustering［C］／／8th International Conference on Computer and Information Technology （ICCIT’05），2005：28－30.

［31］Liu D，Tang Y，Guan X.Texture segmentation using intensified fuzzy Kohonen clustering Network［C］／／Wang L，Chen K，Ong Y S.ICNC 2005，LNCS 3611，2005：75－80.

［32］Yang M S，Hung W L，Chen D H.Self－organizing map for symbolic data［J］.Fuzzy Sets and Systems，2012，203：49－73.

［33］Chen D H，Hung W L，Yang M S.A batch version of the SOM for symbolic data［C］／／2010Sixth International Conference on Natural Computation（ICNC 2010），2010：1－5.

［34］Hung W L，Chen D H，Yang M S.Suppressed fuzzy－soft learning vector quantization for MRI segmentation［J］.Artificial Intelligence in Medicine，2011，52：33－43.

［35］Zhao Q H，Ha M H，Peng G B，et al.Support vector machine based on half－suppressed fuzzy C－means clustering［C］／／Proceedings of the Eighth International Conference on Machine Learning and Cybernetics.Baoding：IEEE，2009：1236－1240.

［36］Srivastava A，Asati A，Bhattacharya M.A fast and noiseadaptive rough－fuzzy hybrid algorithm for medical image segmentation［C］／／IEEE International Conference on Bioinformatics and Biomedicine，2010：416－421.

［37］Srivastava A，Asati A，Bhattacharya M.Fast hybrid rough－set theoretic fuzzy clustering technique with application to multispectral image segmentation［C］／／Proceedings of the First International Conference on Intelligent Interactive Technologies and Multimedia，2010，126－129.

［38］Krinidis S，Chatzis V.A robust fuzzy local information c－means clustering algorithm［J］.IEEE Trans Image Proc，2010，19（5）：1328－1337.

［39］Szilágyi L.Lessons to learn from a mistaken optimization［J］.Pattern Recognition Letters，2014，36（15）：29－35.

［40］Ali M A，Karmakar C C and Dooley S L.Review on Fuzzy Clustering Algorithms［J］.Journal of Advanced Computations，2008，2（3）：169－181.

［41］Ravindraiah R，Tejaswini K.A survey of image segmentation algorithma based on fuzzy clustering［J］.International Journal of Computer Science and Mobile Computing，2013，2（7）：200－206.