相位梯度自聚焦在FFBP聚束SAR处理中的应用
2014-06-09李浩林陈露露邢孟道
李浩林,陈露露,张 磊,邢孟道,保 铮
(西安电子科技大学 雷 达信号处理国家重点实验室,陕西 西 安 710071)
后向投影(Back-Projection,BP)[1-2]的本质是天线相位阵列沿特定方向的波束形成[3].后向投影算法不但适用于线性或非线性航迹,而且重构的图像不存在波前弯曲和几何形变.快速分解后向投影(Fast Factorized Back-Projection,FFBP)算法[4-5]是后向投影算法的快速实现,除了具备上述优势之外,快速分解后向投影算法最显著的特点就是大幅降低了运算量.然而在存在运动误差的情况下,这种通过积分实现方位聚焦的方式会导致后向投影算法和快速分解后向投影算法无法结合自聚焦进行运动补偿[6],原因如下:运动误差引起的图像散焦不沿方位向图像域和距离压缩相位历程域(以下简称相位历程域)之间的傅里叶变换对(Fourier Transform Pairs,FTP)关系不存在.因此,如何使用快速分解后向投影算法进行自聚焦处理是目前亟待解决的问题.
文献[6]使用波束形成(等价于后向投影)在距离-正弦角网格上重建图像,指出在小角域条件下正弦角域与方位时域近似为傅里叶变换对关系,并验证了该方法结合相位梯度自聚焦(Phase Gradient Autofocus,PGA)恢复图像的可能性.然而该方法并未从根本上解决运动误差较大时的图像快速重建问题.文献[7]提出了虚拟极坐标系(距离-正弦角域)的概念,仿真说明了快速分解后向投影算法使用虚拟极坐标系进行图像重构不影响聚焦质量.文献[8]巧妙结合快速分解后向投影算法多孔径递归融合和多孔径图像偏移(Multiple Aperture Mapdrift,MAM)多孔径相位估计的特点,提出了嵌套多孔径图像偏移的快速分解后向投影算法.该方法是基于运动误差的多项式模型提出的,在对高频相位误差进行估计时其性能下降.文献[9-10]以最大图像锐度为优化指标,通过求解聚焦性能代价函数估计运动误差.然而该方法涉及高维参数优化搜索,不具有图像快速重建能力,其实用性受到限制.
笔者提出了一种嵌套相位梯度自聚焦的改进快速分解后向投影算法.首先使用虚拟坐标系作为图像融合平面,并沿视线方向建立局部极坐标系,为相位梯度自聚焦提供图像域与相位历程域之间的傅里叶变换对关系以及最优相位估计方向.其次,充分考虑到改进快速分解后向投影算法角域分辨力由低到高的变化规律,提出了角域低分辨的运动补偿控制角域高分辨的图像散焦的运动补偿思路;通过建立全新的重叠子孔径构型,将相位梯度自聚焦自然地嵌入到改进快速分解后向投影算法的不同阶段.
1 后向投影信号模型
如图1所示,雷达波束始终指向场景中心C,平台以速度v沿x方向匀速直线运动,形成一个长度为L的合成孔径.令t为慢时间,则天线相位中心坐标X =vt.以O为原点建立虚拟极坐标系,P点位于(rp,Θp),其中,Θp=sinθp,则天线到P点的瞬时斜距为
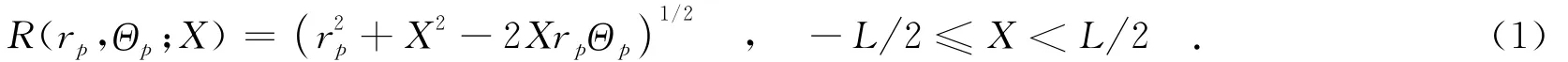
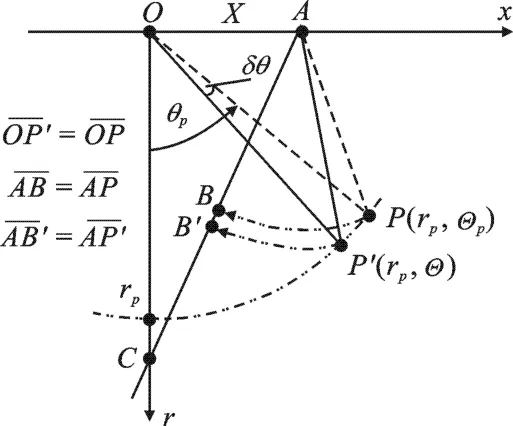
图1 极坐标系下角域位置误差示意图
将P点的回波信号变换到基带并进行距离脉冲压缩,则
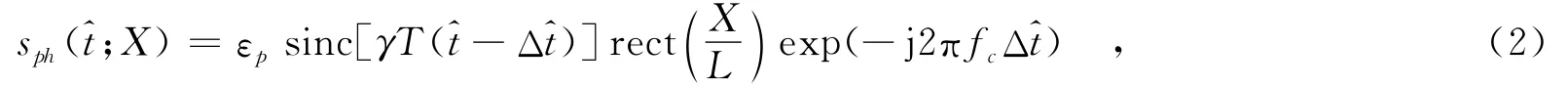
其中,εp为P点的常值复反射系数,rect(·)为窗函数,γ为信号调频率,T为脉冲持续时间为快时间,fc为中心频率,回波延时Δt=2R(rp,Θp;X)c.
由于平台在实际飞行过程中出现偏航和姿态变化,导致P点在虚拟极坐标系(r-Θ 坐 标系,其中Θ=sinθ)下存在距离位置误差和角域位置误差.假设距离位置误差可以由全球定位系统或者惯性测量单元得到有效补偿,且残余的距离位置误差没有超过一个距离单元,因此在下面的分析中只考虑角域位置误差对图像聚焦的影响.如图1所示,理想斜距= R(rp,Θp;X),运动误差使P点的角域位置由Θp变为Θ,则真实斜距=R(rp,Θ;X).由于忽略了距离位置误差,P′点在距离脉冲压缩后仍位于rp距离单元.
下面通过后向投影算法完成sph(t;X)沿斜距历程R(rp,Θ;X)的相干积累,得到(rp,Θ)处的脉冲响应为

其中,λ为波长,ΔR(rp,Θ;X)为斜距误差(见图1的BB′).ε′p为受运动误差调制的复反射系数,表示成

其中,φ为相位误差,是X或t的函数,也是下面需要用自聚焦算法估计的相位.
假设雷达工作在远场,结合式(1)对ΔR(rp,Θ;X)进行关于X的二阶泰勒级数展开,即

其中,X和X2项分别等效为运动误差引起的距离走动和距离弯曲.
若式(5)可以忽略X2项,则式(3)可简化为
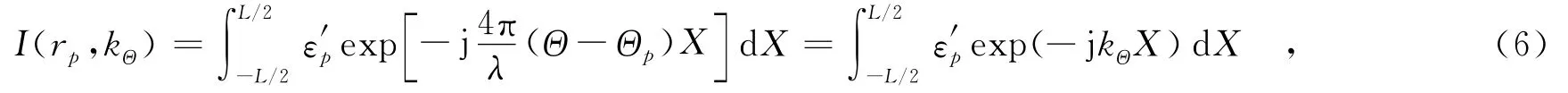
其中,kΘ=4π(Θ-Θp)λ,对应方位波数.式(6)直观地反映了受运动误差破坏的距离压缩数据ε′p可以关于X进行傅里叶变换得到脉冲响应I(rp,kΘ),即建立了图像域与相位历程域之间的傅里叶变换对关系.由于傅里叶变换对关系是相位梯度自聚焦的必要条件,下面将推导傅里叶变换对关系成立的约束条件.
根据文献[2],当运动误差引起的距离走动量不超过一个距离分辨单元时,可以忽略距离弯曲量.由于孔径两端对应最大的距离走动量,则

其中,ρr= c ( 2B),ρr为距离分辨率,B为信号带宽.
令θ=θp+δθ,其中δθ为角域位置误差.假设δθ足够小,使得sinδθ与δθ近似相等,则
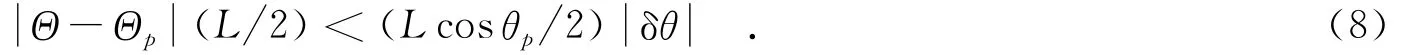
联合式(7)和式(8),则

其中,Q=fcB,为中心频率带宽比;ρθ=λ ( 2Lcosθp),为角域分辨率[1].
由于角域位置误差δθ可正可负,存在双边特性,则

即角域位置误差引起的散焦小于4Q个角域分辨单元时,可以忽略式(5)中X2项,得到如式(6)所示的图像域与相位历程域之间的傅里叶变换对关系.以中心频率为10GHz、信号带宽为1GHz的X波段正侧视聚束合成孔径雷达为例,其中心频率带宽比为10.若使用相位梯度自聚焦对该数据进行相位估计,则虚拟极坐标系下的图像散焦必须小于40个角域分辨单元才能保证傅里叶变换对关系成立.然而对于角域分辨力极高的聚束合成孔径雷达来说,图像散焦可能超过几百个角域分辨单元,这显然违背了式(10)的约束.根据式(9),角域分辨力越低,可容忍的图像散焦越大.考虑到快速分解后向投影算法角域分辨力随图像递归融合由低到高的变化规律,当图像的角域分辨力低时,一定存在图像散焦小于4Q个方位分辨单元的情况;如果该图像被重建在虚拟极坐标系上,那么快速分解后向投影算法下的自聚焦处理的问题将迎刃而解.
2 改进快速分解后向投影算法
笔者在快速分解后向投影算法的基础上进行改进,提出了使用虚拟极坐标系进行图像融合的改进快速分解后向投影算法.由于没有改变快速分解后向投影算法孔径分解、波束形成和图像递归融合的基本框架,改进快速分解后向投影算法也具有角域分辨力随图像递归融合由低到高的变化规律.在满足约束条件的情况下,虚拟极坐标系的使用又可以提供相位梯度自聚焦所需的图像域与相位历程域之间的傅里叶变换对关系,为改进快速分解后向投影算法与相位梯度自聚焦的有效结合奠定了基础.改进快速分解后向投影算法将后向投影算法在全孔径上的积分分割成有限、等长孔径上的分步、分段积分,因此第1节关于相位梯度自聚焦所需的傅里叶变换对关系及约束条件的推导在改进快速分解后向投影算法中仍然成立.
改进快速分解后向投影算法使用虚拟极坐标系代替快速分解后向投影算法的极坐标系,即使用Θ(Θ=sinθ)轴作为虚拟极坐标系的横轴.根据瞬时多普勒fd=2vΘλ知,fd与Θ仅存在常数倍的差异.因此,使用虚拟极坐标系不但具有明确的物理意义,而且在小角域范围内重构的图像可以近似认为位于距离-多普勒域.令角域带宽为Bd,则角域范围为
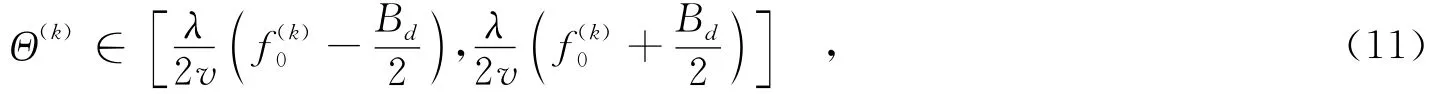
为了满足相位梯度自聚焦的相位估计需求,改进快速分解后向投影算法还对坐标系的建立方式进行了改进,创新地沿子孔径中心到场景中心的视线方向建立局部虚拟极坐标系.如图2所示,第i处理阶段第k(k为偶数)个孔径的中心为,到场景中心的视线角为,而第k-1个孔径的中心为,到场景中心的视线角为,虚拟极坐标系如扇形区域所示.若改进快速分解后向投影算法进行基2图像融合,则第i+1处理阶段第k 2个孔径的中心为,到场景中心的视线角为.图2直观地展示了坐标系a和坐标系b向坐标系c的融合过程,而本质上实现了和方向的波束在方向的波束形成.
以第i处理阶段第k个子孔径为例.假设孔径中心为A(k),孔径长度

图2 图像融合前后虚拟极坐标系的变化
为d,孔径位置个数为Ns,则孔径中心时刻为=A(k)v,孔径时间Ts=NsFPR,数据域的孔径时间范围为

其中,t(k)的离散时间间隔为1 FPR,FPR为脉冲重复频率.
使用改进快速分解后向投影算法对上述子孔径数据进行聚焦,得到子图像为
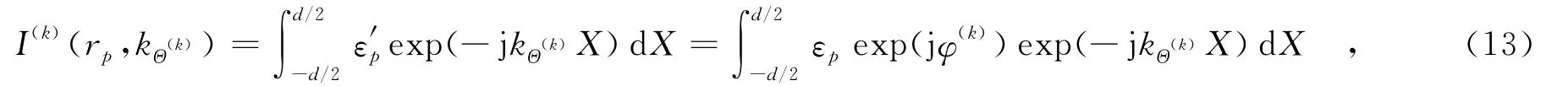
其中,kΘ(k)为第i处理阶段第k个子孔径对应的方位波数,φ(k)为相位误差.
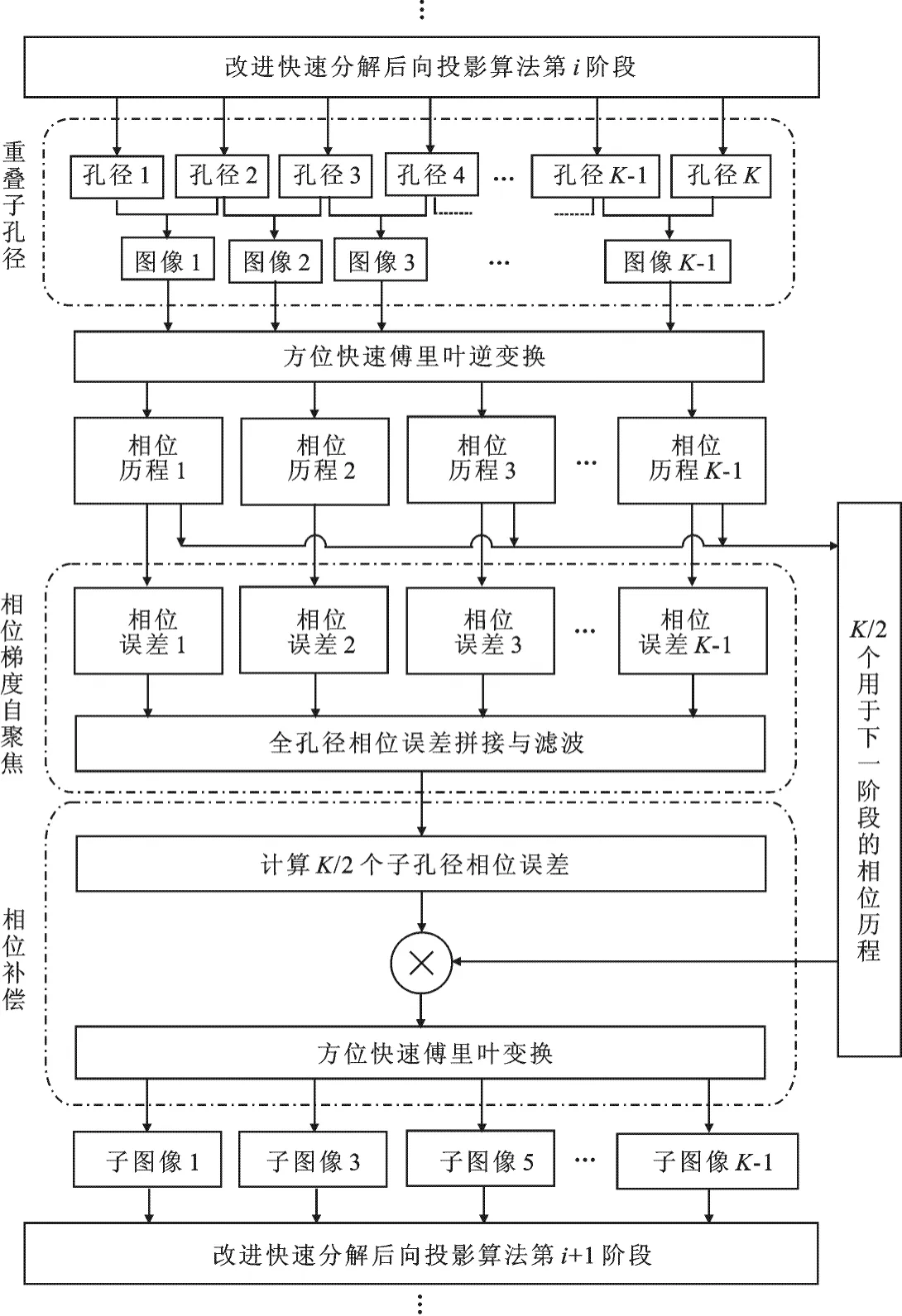
图3 嵌套多孔径相位梯度自聚焦的改进快速分解后向投影算法自聚焦处理流程
3 改进快速分解后向投影算法自聚焦处理
相位梯度自聚焦是合成孔径雷达成像运动补偿中最常用的自聚焦方法之一,具有很高的精度和鲁棒性[11-12].虽然相位梯度自聚焦循环移位操作消除了相位误差的线性分量,但是相邻子孔径间仍存在线性相位差异.如果使用子孔径相位误差直接对子图像进行相位补偿,相邻孔径间存在的线性相位差异势必会引起子图像间的相对偏移,即引入了角域位置误差,从而不利于相位梯度自聚焦的收敛和图像质量的逐步提高.为了避免该情况的发生,首先要根据子孔径相位误差获得全孔径相位误差函数,然后根据各子孔径中心时刻重新解算出子孔径相位误差,从而消除了子孔径相位误差之间的线性相位分量,避免了图像偏移.然而,要获得全孔径相位误差函数,需要相邻孔径间存在重叠的相位历程.
重叠子孔径最早结合极坐标算法(PFA)用于校正聚束合成孔径雷达空变的波前弯曲效应[13],之后被广泛用于相位估计[14].考虑到改进快速分解后向投影算法的结构特点,笔者提出了一种适用于改进快速分解后向投影算法的全新的重叠子孔径构型建立方法,较好地衔接了改进快速分解后向投影算法和相位梯度自聚焦相位估计,如图3所示.
(1)在初始阶段按照一定系数将全孔径分解为若干较短的子孔径,孔径和数据均不存在重叠.
(2)在处理阶段进行重叠子孔径操作.假设第i处理阶段有K(K为偶数)个子孔径,任意相邻的两个孔径进行图像融合可以得到K-1幅子图像,其中K2幅用于改进快速分解后向投影算法下一阶段的图像融合.此后继续按照该方式建立重叠子孔径构型,孔径重叠率始终为1/2.
(3)最后两个孔径不进行重叠子孔径操作,通过图像融合直接得到一幅角域全分辨图像,然后使用相位梯度自聚焦直接进行相位估计和补偿.
利用重叠子孔径进行相位估计的基本操作有:全孔径划分为重叠子孔径、子孔径相位误差估计、孔径间线性相位消除、全孔径相位误差拼接以及全孔径相位误差补偿.如图3所示,第i阶段的重叠子孔径构型可得到K-1幅子图像,其中有K2幅用于下一阶段的图像融合.使用相位梯度自聚焦对K - 1幅子图像进行估计,可得到,…等 K - 1个子孔径相位误差.使用重叠子孔径可以消除相邻孔径重叠部分的线性相位差异,实现相位误差的连续拼接和滤波[15],最终得到全孔径相位误差,如图4所示.由于全孔径相位误差是方位时间t的函数,根据每幅子图像的孔径中心时刻t0(k),可计算出K2个子孔径相位误差函数.

图4 全孔径相位误差拼接示意图
4 实验分析与验证
为了验证上述方法的有效性,下面使用X波段聚束合成孔径雷达数据进行处理,其中心频率带宽比Q=6,详细参数如表1所示.在进行数据处理时,使用的距离采样点数为4 096,可忽略距离空变性.根据表1参数,距离分辨率为0.13m,方位分辨率为0.28m.

表1 X波段雷达参数

图5 自聚焦处理前后的成像结果对比
在改进快速分解后向投影算法的初始阶段,子孔径的方位脉冲数为128个.在处理阶段的初期,由于角域分辨力较低,图像散焦小于6个方位分辨单元,而该数据允许的相位梯度自聚焦估计的最大图像散焦为24,因此6个方位分辨单元的图像散焦满足相位梯度自聚焦的约束条件.随着递归融合的进行,之后处理阶段的图像散焦始终小于10个方位分辨单元,因此相位梯度自聚焦进行相位估计的窗宽只需略大于10,非常有利于相位估计的快速收敛,这与频域算法自聚焦处理相比具有显著优势.图5(a)为使用改进快速分解后向投影算法未进行运动补偿的成像结果,图5(b)为使用笔者提出的方法处理得到的成像结果.为了获得良好的视觉效果,沿距离向进行二视处理,使二维分辨率接近.由图5(a)可以发现,改进快速分解后向投影算法不结合自聚焦处理进行运动补偿的图像存在严重的方位散焦.图5(b)的图像得到了良好的聚焦,运动误差基本得到了校正.由于图5(b)的熵值小于图5(a)的熵值,说明笔者提出的方法对图像质量的改善效果明显.将不同阶段相位梯度自聚焦估计的相位误差相加,得到最终的相位误差,将其换算为斜距误差,得到如图6所示的结果.虽然斜距误差变化范围仅有0.3m,但在高分辨、长CPI的情况下,即使如此小的运动误差也足以引起图像的严重散焦和几何失真.而且这么小的斜距误差已经超出现阶段大多数运动测量系统的精度,从而有力地说明基于数据的自聚焦处理在高分辨合成孔径雷达成像中的必要性.
图7中的图像分别对应图5(a)和图5(b)中方框所示区域的局部放大结果.利用图7中椭圆框内的特显点进行方位响应分析,得到方位剖面如图8所示,虚线为使用改进快速分解后向投影算法未进行运动补偿的方位响应,实线为使用笔者提出的方法的方位响应.显然,使用笔者提出的方法的方位响应不但非常接近“sinc”形式,而且具有较好的旁瓣性能.
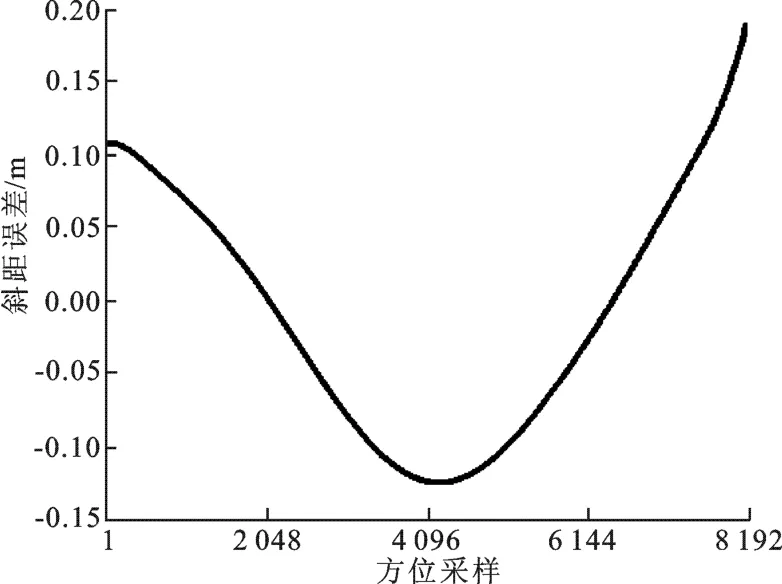
图6 笔者提出的方法估计的斜距误差
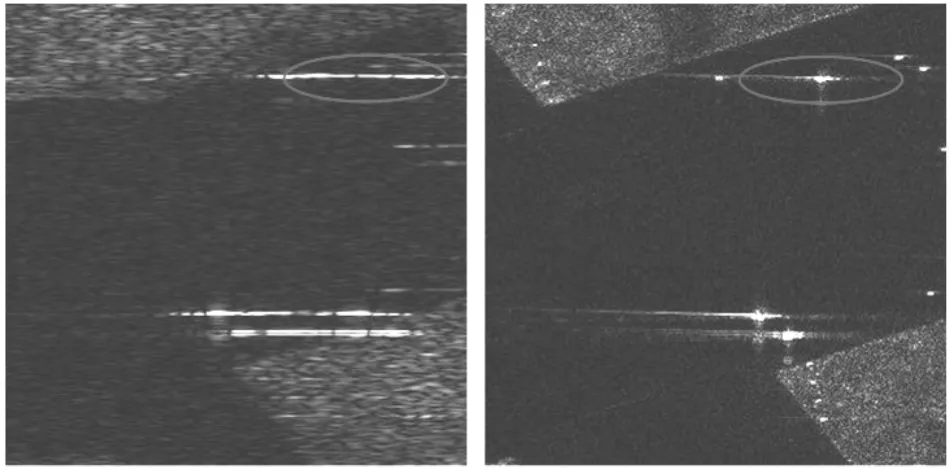
图7 局部放大结果
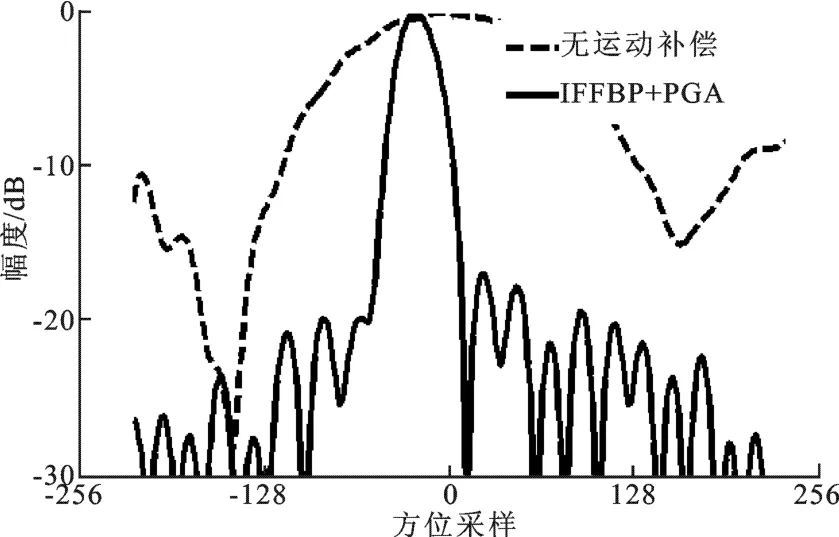
图8 点目标方位剖面
5 结束语
笔者将虚拟极坐标系作为子孔径递归融合平面,为相位梯度自聚焦提供了图像域与相位历程域之间傅里叶变换对关系;创新地沿视线方向建立虚拟极坐标系,为相位梯度自聚焦提供了最优的相位估计方向.建立了全新的重叠子孔径框架,巧妙地衔接了改进快速分解后向投影算法和多孔径相位梯度自聚焦,将相位梯度自聚焦嵌套到改进快速分解后向投影算法递归融合的不同阶段.最后,通过实测数据的处理结果和图像质量的定量分析验证了笔者提出方法的可行性.
[1] Munson D C Jr,O'Bruen J D,Jenkins W K.A Tomographic Formulation of Spotlight-mode Synthetic Aperture Radar[J].Proceedings of the IEEE,1983,17(8):917-925.
[2] Desai M D,Jenkins W K.Convolution Backprojection Image Reconstruction for Spotlight Mode Synthetic Aperture Radar[J].IEEE Transactions on Image Processing,1992,1(4):505-517.
[3] Jakowatz C V Jr,Wahl D E,Yocky D A.Beamforming as a Foundation for Spotlight-mode SAR Image Formation by Backprojection[C]//Proceedings of SPIE:6970.Bellingham:SPIE,2008:69700Q.
[4] Ulander L M H,Hellsten H,Stenström G.Synthetic-aperture Radar Processing Using Fast Factorized Back-projection[J].IEEE Transactions on Aerospace and Electronic Systems,2003,39(3):760-776.
[5] 李杨寰,宋千,王鹏宇,等.多级多分辨快速后向投影成像算法 [J].电子学报,2011,39(3):518-524.Li Yanghuan,Song Qian,Wang Pengyu,et al.Multi-stage Multi-resolution Fast Back-projection Imaging Algorithm[J].Acta Electronica Sinica,2011,39(3):518-524.
[6] Jakowatz C V Jr,Wahl D E.Considerations for Autofocus of Spotlight-mode SAR Imagery Created Using a Beamforming Algorithm [C]//Proceedings of SPIE:7337.Bellingham:SPIE,2008:73370A.
[7] 李浩林,张磊,杨磊,等.一种改进的快速分解后向投影SAR成像算法 [J].电子与信息学报,2013,35(6):1435-1441.
Li Haolin,Zhang Lei,Yang Lei,et al.A Novel Fast Factorized Back-projection Algorithm for Synthetic Aperture Radar Imagery[J].Journal of Electronics &Information Technology,2013,35(6):1435-1441.
[8] 张磊,李浩林,邢孟道,等.快速后向投影合成孔径雷达成像的自聚焦方法 [J].西安电子科技大学学报,2014,41(1):87-94.
Zhang Lei,Li Haolin,Xing Mengdao,et al.Autofocusing Synthetic Aperture Radar Imagery with Fast Back-projection Algorithm [J].Journal of Xidian University,2014,41(1):87-94.
[9] Hellsten H,Dammert P,Åhlander A.Autofocus in Fast Factorized Backprojection for Processing of SAR Images When Geometry Parameters Are Unknown [C]//Proceedings of the IEEE Radar Conference.Piscataway:IEEE,2010:603-608.
[10] Ash J N.An Autofocus Method for Backprojection Imagery in Synthetic Aperture Radar[J].IEEE Geoscience and Remote Sensing Letters,2012,9(1):104-108.
[11] Wahl D E,Eichel P H,Ghiglia D C,et al.Phase Gradient Autofocus—a Robust Tool for High Resolution Phase Correction[J].IEEE Transactions on Aerospace and Electronic Systems,1994,30(3):827-835.
[12] Carrara W G,Goodman R S,Majewski R M.Spotlight Synthetic Aperture Radar:Signal Processing Algorithm [M].Boston:Artech House,1995.
[13] Burns B L,Cordaro J T.A SAR Image-formation Algorithm that Compensates for the Spatially-variant Effects of Antenna Motion[C]//Proceedings of SPIE.Bellingham:SPIE,1994:14-24.
[14] Zhu Daiyin,Jiang Rui,Mao Xinhua,et al.Multi-subaperture PGA for SAR Autofocusing[J].IEEE Transactions on Aerospace and Electronic Systems,2013,49(1):468-488.
[15] 张磊.高分辨SAR/ISAR成像及误差补偿技术研究 [D].西安:西安电子科技大学,2012.
