典型管节点的疲劳寿命评估

徐小燕，胡芳，赖芳，王庆丰

(1.江苏科技大学船舶与海洋工程学院，江苏镇江212003;2.沪东中华造船集团有限公司，上海 200129; 3.大连船舶重工集团有限公司，辽宁大连 116000)

典型管节点的疲劳寿命评估

徐小燕1，胡芳2，赖芳3，王庆丰1

(1.江苏科技大学船舶与海洋工程学院，江苏镇江212003;2.沪东中华造船集团有限公司，上海 200129; 3.大连船舶重工集团有限公司，辽宁大连 116000)

针对大型焊接结构在复杂的应力应变场中，结构应力集中的地方往往会萌生裂纹，裂纹扩展损伤积累到一定的程度就会很容易酿成灾难性事故的问题，提出了一种运用权函数法求解典型管节点的应力强度因子，采用单一裂纹扩展率曲线模型预估管节点的疲劳寿命。通过与经验公式的结果对比，发现权函数的方法在计算寿命的时候和经验公式的结果拟合度很好，而且寿命要比经验公式偏小，更有利于对寿命的保守估计。该方法简单方便，具有很强的操作性和可行性。

疲劳断裂;疲劳曲线;应力强度因子;权函数

0 引言

近年来，随着我国经济的高速发展，船舶运输量也急剧增加，与此同时，水上安全生产形势也面临严峻的考验。由于船舶和海洋平台都是大型的焊接结构，海洋平台结构庞大，在海洋中受力复杂，所以长期处于波浪力、风力、潮流力等交变载荷的作用下［1］。结构应力集中的地方往往会萌生裂纹，裂纹扩展损伤积累到一定的程度就很容易酿成灾难性的事故，以往就存在着许多脆性破坏和疲劳断裂引起的海洋平台以及船体事故，影响了经济效益，造成坏的社会影响。

1 典型节点疲劳寿命的研究现状及意义

船舶及海洋工程结构物长期处在循环载荷作用下容易产生疲劳裂纹，随着裂纹的扩展将导致其断裂或失效，会带来灾难性事故［1］。目前国内外关于疲劳已经有很多的研究方法，主要包括理论计算法、数值仿真法、试验方法，其中主要的又有S－N曲线方法和断裂力学法。

确定疲劳裂纹扩展率曲线是基于断裂力学预测疲劳寿命的关键。关于裂纹扩展率模型的研究已经有了不少成果，近年来以Paris公式为基础，将应力比、裂纹尖端闭合效应、载荷次序效应和应力强度因子门槛值考虑在内，许多学者提出了自己的模型。而Forman公式和Walker公式又提出了应力比影响的修正公式，目前，对载荷迟滞效应的研究主要有Wheeler模型和Willenborg模型。而应力强度因子是在裂纹扩展率模型确定的情况下影响疲劳寿命的预估准确性的主要因素。简单结构形式的应力强度因子的求解，已经有许多的学者提出了比较成熟的方法，应力强度因子的经验公式最具代表性的是在Newman-Raju(1979)拉弯应力作用下表面裂纹应力强度因子计算公式，它计算精度高，适用范围广。对于复杂结构的应力强度因子的求解，也有一些学者采用不同的方法进行研究，例如运用有限元方法对裂纹体建模，应用交互J积分方法和位移外推插值法直接估算应力强度因子，再运用断裂力学方法预测它的疲劳寿命。但这些方法需要对裂纹体建模而且对网格的划分也有很高的要求，耗费了大量的工作时间，可操作性低［2］。

基于国内外对应力强度因子的研究现状，本文提出了把运用权函数方法求解得到的应力强度因子用于预估典型管节点的疲劳寿命，以T型管节点为对象开展研究。

2 裂纹的扩展和寿命评估的计算

2.1 疲劳裂纹的扩展速率

疲劳裂纹的扩展率是指在疲劳裂纹的缓慢扩展阶段内每一次应力循环裂纹所扩展的距离，该速率用Δa/ΔN(mm/周)表示。其中，Δa表示为应力循环ΔN次后裂纹扩展的长度，用微分da/dN表示。

在断裂力学中，应力强度因子和裂纹长度的关系表达式为:

式中:K为应力强度因子;a为裂纹长度;σ为对应的应力;Y为结构形式有关的参数。若将上述概念用于疲劳，则有:

式中:Kmax为最大循环应力所对应的应力强度因子; Kmin为最小循环应力所对应的应力强度因子;ΔK为裂纹前沿应力场强度因子幅。

在一定循环应力条件下，已知一定裂纹扩展长度，就可以求出和它相对应的裂纹扩展速率da/dN，而同时也能求出在一定循环应力条件下的裂纹尖端的应力场强度因子幅ΔK。

而第二阶段也是最主要的阶段，它是疲劳裂纹扩展寿命的主要组成部分。一般认为，在数学坐标系中da/dN与ΔK呈线性的关系是一条直线(也可用2条直线来描述)，其中Paris公式是其中运用得最为广泛的一种，表示为:

式中:C和m一般通过实验测得，是有关实验条件如环境、频率、温度、应力比等的材料参数。

基于断裂力学理论，本文选取黄小平提出的单一裂纹扩展率曲线模型，建立应力强度因子幅值与疲劳裂纹扩展速率的函数关系表达式，根据材料的断裂韧性预测T型管节点的疲劳寿命，并将结果与手册中的K用于预估的疲劳寿命结果相比较。

式中:ΔKcqo、ΔKtho分别是当应力比R=0时的等效应力强度因子幅和应力强度因子幅门槛值;C是Paris系数;m是与裂纹扩展有关的指数。

式中:MR是载荷比的修正因子;Mp是载荷次序的修正因子。

MR在wake模型的基础上修正了载荷比R效应的模型:

式中:β、β1为形状系数;aOL是过载时的裂纹半长;ry是裂纹尖端塑性区大小;rOL是过载时裂纹尖端塑性区大小;rΔ是低载-过载引起的裂纹尖端塑性区大小的增量。

船海结构物在服役过程中受到的外力是不断变化的，因而R也是不断变化的。通过对MR的计算证明，该模型能更好地描述不同应力比下的裂纹扩展数据［3］。

2.2 裂纹的扩展和寿命评估的计算

本文基于有限元软件ANSYS和权函数结合的方法对典型管节点结构的裂纹扩展路径进行数值模拟，具体计算过程如下:

(1)运用有限元软件对典型节点进行结构建模，并施加边界条件和载荷，确定结构的应力集中区域。

(2)在典型结构的应力集中区域进行定义裂纹初始长度a0的扩展路径，通过第一主应力原则，映射第一主应力的分布到路径上，得到裂纹厚度方向的应力分布，通过函数拟合求出假想裂纹处在无裂纹情况下沿裂纹方向的应力分布函数σx，带入权函数公式算出。

(3)在裂纹长度a0的基础上，增加一个大小为a1的裂纹，通过相同的方法计算出K1I的值。

(4)重复(3)的过程，直至其应力强度因子小于断裂韧性K1C。

(5)拟合得到的数据，代入计算疲劳寿命。

由于应力强度因子K与裂纹长度的关系为:

式中:F为施加的载荷。

3 典型节点的疲劳寿命估算

3.1 材料和有关参数的确定

本文选取Q235钢作为管节点的材料，16 mm＜板厚≤40 mm，屈服强度为225 MPa，断裂韧性KIC=;参数的选择使用BS7910的平均曲线，得到C=9.58×10－9，m=2.74，R=0.9，ΔKth0= 3.2［5］，根据计算得到的应力强度因子。本文用单一曲线模型在不考虑载荷次序效应和残余应力的情况下得到给定裂纹长度下的扩展率，分别对裂纹扩展率公式进行拟合。

3.2 T型管节点的寿命估算

3.3.1 求解应力强度因子幅值

应用权函数法求解应力强度因子首先要求解假想裂纹表面应力分布函数σx。通过有限元软件ANSYS建模，得到T型管节点的应力分布，发现最大应力值为154 MPa，并没有超过材料屈服极限225 MPa。通过提取沿裂纹扩展方向的第一主应力，经数值软件进行数值拟合，可得到沿裂纹扩展方向的节点表面的第一主应力分布函数σx。

3.3.2 疲劳裂纹扩展寿命计算

已知初始裂纹长度，通过模拟裂纹的扩展路径拟合第一主应力的分布函数σx，代入权函数计算它的应力强度因子。下面通过Origin软件拟合得到裂纹扩展深度与应力强度因子的关系见图1和图2。

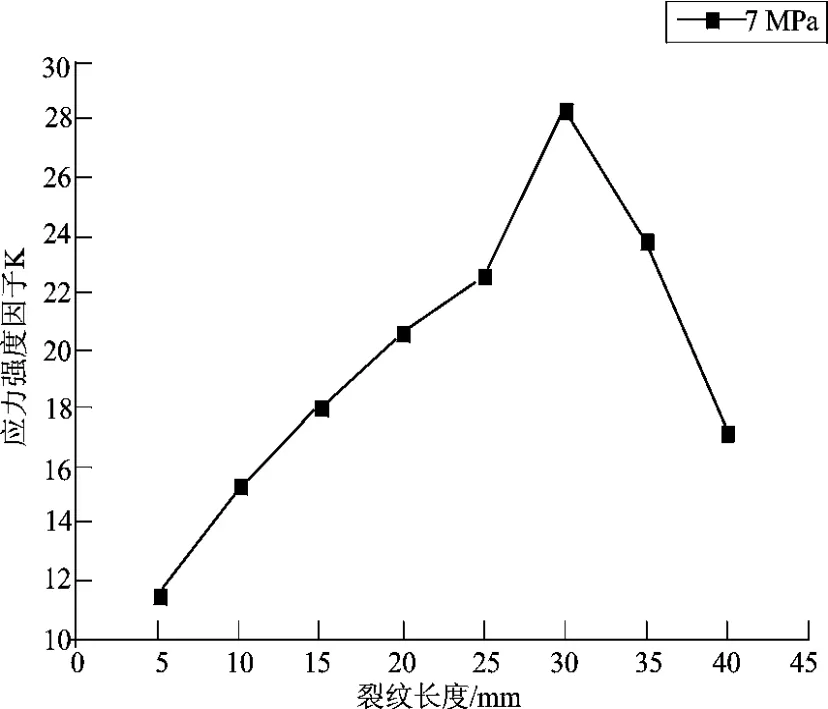
图1 裂纹长度和应力强度因子曲线(7 MPa)

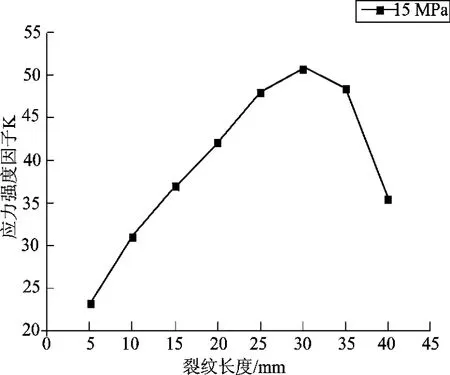
图2 裂纹长度和应力强度因子曲线(15 MPa)

已知裂纹的初始尺寸，通过计算得到裂纹尖端的应力强度因子K，然后判断应力强度因子是否满足脆性断裂K准则，如果小于断裂韧性则需要求解下一个裂纹增量所对应的应力强度因子K。通过叠加增量得到新的裂纹尺寸，计算出新的应力强度因子。重复上述的步骤直到裂纹尖端应力强度因子满足脆性断裂K准则，则计算结束，分别得到在两种载荷下的疲劳寿命，如图3、图4所示。

图3 管节点的寿命评估(15 MPa)

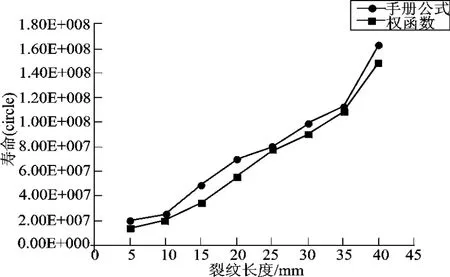
图4 管节点的寿命评估(7 MPa)

4 结语

本文提出了一种将权函数方法用于计算典型管节点的应力强度因子，以典型的T型管节点为例进行有限元建模，简化了它在复杂应力场中的应力分布，提取了裂纹最深处的一条第一主应力分布，通过数值拟合应力分布函数代入权函数计算得到它的应力强度因子，将计算出来的应力强度因子幅带入疲劳扩展寿命计算模型预估它的疲劳寿命。通过比较发现，权函数的方法在计算寿命的时候和经验公式的结果拟合度很好，而且寿命要比经验公式偏小，更有利于对寿命的保守估计。

［1］金伟良，龚顺风，朱俊民.海洋平台结构管节点强度可靠性分析［J］.科技通报，2002，9(5):349－354.

［2］赵邦杰.基于权函数法的焊接结构疲劳裂纹扩展寿命计算［D］.大连:大连理工大学，2013.

［3］Huang X P，Moan T.Improved modeling of the effect of R-ratio on crack growth rate［J］.Int.J Fatigue，2007，29:591－602.

［4］赵章焰，吕运冰，孙国正.J积分法测量低碳钢Q235的断裂韧性KIC［J］.武汉理工大学学报，2002，24(4):111－112.

［5］赵邦杰.基于权函数法的焊接结劳裂纹扩展寿命计算［D］.大连:大连理工大学，2013.

U661.4

A

2013-12-28

徐小燕(1988－)，女，硕士研究生，研究方向为船舶结构设计及强度;胡芳(1974－)，女，高级工程师，研究方向为船体设计;赖芳(1974－)，女，工程师，研究方向为船舶制造及管理;王庆丰(1976－)，男，副教授，硕士生导师，主要研究方向为船舶结构设计及强度、船舶制造工艺力学。