一种直边缘物体宽度的图像测量法

张铁英，白福忠，宋小燕，武建新，甘世明

（内蒙古工业大学机械学院，内蒙古呼和浩特010051）

一种直边缘物体宽度的图像测量法

张铁英，白福忠，宋小燕，武建新，甘世明

（内蒙古工业大学机械学院，内蒙古呼和浩特010051）

提出一种基于方向功率谱与投影梯度的直边缘物体宽度测量方法，通过对目标图像功率谱进行极坐标变换得到方向功率谱，并由此计算出直边缘物体的伸展方向；然后对原始图像按照该伸展方向进行灰度投影，并由投影梯度结果得到待测宽度。该方法无需对目标图像进行边缘检测、阈值分割等预处理操作，因而测量结果更加准确、可靠，且计算量较小、测量效率高。数值模拟与实验结果表明，本文所提方法能够保证1像素的测量精度，且物体长度方向的几何尺寸不影响宽度测量结果。

宽度测量；方向功率谱；投影梯度

1 引 言

在工程实际中存在着大量的直边缘物体，如板材、方槽、纸张以及一些矩形精密零件，并且均需要对其宽度进行精确测量。对于传统接触式测量方法，主要存在测量精度不高、测量过程繁琐等缺陷，且不适用于精密零件以及柔性物体的测量［1］。近年来，随着机器视觉理论与计算机技术的发展，视觉测量技术已成为非接触测量领域最具发展潜力的新技术，由于具有非接触、高速率、动态范围大、结果可靠等优点，非常适合于传统方法难以适用的场合［2］。

目前，基于机器视觉的直边缘物体宽度测量方法，需要对目标图像进行边缘检测与细化处理，得到1像素宽的轮廓图像，然后利用Hough变换进行直线检测，进而得到图像中物体宽度，如文献［3］～［5］中的方法均利用了该方案；该方法处理步骤较多，计算量大，测量效率不高，实用性差；另外，处理过程中用到阈值处理，当阈值选取不当时将导致边缘检测不准确，测量可靠性与精度受到影响。基于灰度投影积分法的直线检测方法［6］，避免了传统测量方法中阈值处理问题，但是需要对图像按照不同角度进行方向投影，计算量大；并且投影时选取的角度步长对测量精度与速度有很大影响。

本文基于方向功率谱与投影梯度理论，提出一种直边缘物体宽度的图像测量法，首先对图像功率谱进行极坐标变换得到方向功率谱，计算出直边缘物体的伸展方向，即直边缘与水平方向之间的夹角；然后对原始图像在该伸展方向上进行灰度投影，并根据投影梯度结果计算出物体宽度。

2 方法原理

本文所提方法主要包括下面两个技术步骤。

2.1 基于方向功率谱的直边缘物体伸展方向计算

2.1.1 二维离散傅里叶变换的位移性和旋转性

一幅M×N像素的数字图像f（x，y）的二维离散傅里叶变换（DFT）以及功率谱分别表示为：

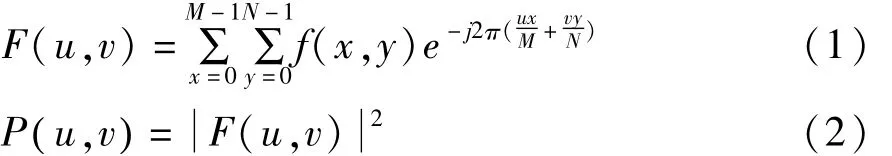
二维DFT的位移性表明，空域图像产生位移时，仅会导致频域中相位发生变化，而位移前后图像具有相同的功率谱，并且功率谱的零频总会位于功率谱图像的中心位置。其次，二维DFT的旋转性表明，空域图像旋转某一角度，其功率谱旋转相同的角度［7］。同时，对于直边缘物体，其空域图像中直边缘的法线方向对应于功率谱中局部最大能量的延伸方向。基于以上讨论，可以根据下面引入的方向功率谱来计算直边缘物体的伸展方向。

2.1.2 方向功率谱以及物体伸展方向计算

为了从功率谱中计算出对应直边缘物体的伸展方向，需要以功率谱图像中心为原点，对每一给定大小扇角内的能量进行累加求和，以寻找局部最大能量的延伸方向。为了简化求解过程，将笛卡尔坐标系下表示的功率谱转化到极坐标系中，变换公式表示为［8］：

式中，u，v和r，φ分别表示笛卡尔坐标系和极坐标系下的坐标变量。r的物理意义是指笛卡尔坐标系中某一点u，()v相对于原点所形成矢量的幅值；φ表示该矢量的幅角，当φ≥180°时，φ＝φ－180。二维DFT的共轭对称性说明功率谱相对于原点对称；因此，φ的取值位于0°～179°。通过极坐标变换将笛卡尔坐标系中相对于原点的旋转量转化为极坐标系中沿φ轴的平移量［9］。

如图1所示功率谱极坐标变换示意图中，笛卡尔坐标系中一点对应于极坐标系中一点，二者的位置关系由公式（3）所决定；笛卡尔坐标系中的圆（圆心位于坐标原点）映射为极坐标系中沿φ轴的直线（水平线）；笛卡尔坐标系中经过原点的斜线映射为极坐标系中沿r轴的直线（纵向线）［10］。

图1 功率谱极坐标变换示意图

将极坐标系下的功率谱按纵向进行累加，得到：

E(φ)表示每一幅角方向上的能量分布，即方向功率谱；而方向功率谱最大值Emax对应的φ值则对应于直边缘的法线方向，将其减去90°即可得到直边缘物体的伸展方向。

2.2 基于灰度投影梯度的直边缘物体宽度测量

数字图像f（x，y）在某一方向上的灰度投影公式表示为：

式中，x′＝x cosα－y sinα，y′＝x sinα＋y cosα，α为投影方向与x轴之间的夹角；当α＝0°和90°时，分别表示水平投影和垂直投影。于是，水平投影的表达式为：

水平投影与方向投影示意图如图2所示，图中f（x，y）表示原始图像，R0为水平投影，Rα为沿x′轴方向的投影。

由于图像中目标与背景的灰度存在明显差异，反映在方向投影曲线中将出现较大阶跃变化，这种变化可以通过梯度运算来检测。方向投影Rα的梯度由一阶导数（即差分）来得到：

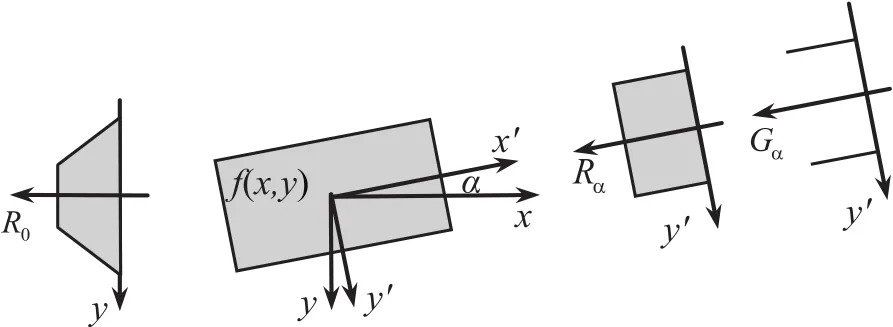
图2 灰度投影及其梯度示意图

图2 右图中Gα为方向投影Rα的梯度，由图可见，投影梯度曲线中出现明显的峰值，同时峰值点位置与直边缘相对应；而峰值点位置之差即为待测直边缘物体的宽度。

3 方法精度分析

通过计算机仿真设计一系列大小为128×128像素的图像，图像中均包含一个大小为30×90像素的矩形图案。第一幅图像中矩形图案水平放置，即矩形图案的长边沿水平方向；之后每一幅图像中的矩形图案依次顺时针旋转5°，旋转范围为0°～175°。然后按照2.1节介绍的方法计算每一幅图像的方向功率谱，其中一幅矩形图案旋转角度为5°的仿真图像及其功率谱、功率谱极坐标变换结果与方向功率谱如图3所示。

进一步确定每一幅仿真图像对应方向功率谱的最大值出现的位置，从而计算出相应图像中所含矩形图案的伸展方向。例如，图3（d）所示方向功率谱中最大值Emax所对应的φ值等于94.91°；将其减去90°后的结果为4.91°，该数值即为图3（a）所含矩形图案的伸展方向。计算结果与给定的理论旋转角度之差表示伸展方向计算误差，结果如图4所示。图4显示，伸展方向的最大计算误差等于0.2°。该数值仿真过程给出了方向功率谱法的计算精度。

图3 仿真图像及其方向功率谱计算图示

图4 伸展角度计算误差

根据计算出的伸展角度，对原始仿真图像进行方向投影并计算投影梯度，由此可以得到仿真图像中矩形图案的宽度值。其中，图3（a）所示仿真图像的方向投影与投影梯度如图5所示。根据投影梯度法测量出所有仿真图像所含矩形图案的宽度均等于30像素，该测量结果与给定理论数据完全吻合。

图5 图3（a）所示仿真图像的方向投影与投影梯度

此外，我们设计了三种不同长度的矩形图案，其大小分别为30×60像素、30×150像素和30×210像素，生成的仿真图像大小均为256×256像素；矩形图案的理论旋转角度均设为－25°；在伸展方向计算误差为0.2°的情况下，计算仿真图像的灰度投影梯度，以验证直边缘物体长度对灰度投影梯度法的影响。经过计算，长度不同的三个矩形图案的宽度测量结果均等于30像素。

上述精度分析结果说明，本文所提方法的伸展方向计算误差为0.2°、能够保证1像素的尺寸测量精度，并且待测直边缘物体几何尺寸不影响宽度测量结果。

4 直边缘物体宽度测量实验

实验中对一个槽型物体进行宽度测量，为了体现测量方法的有效性，专门将槽型物体与x轴方向保持一个倾斜角度，实验图像如图6（a）所示。由图6（b）所示实验图像的方向功率谱计算出的物体伸展方向等于－13.3°。图6（c）和图6（d）分别表示实验图像的方向投影与投影梯度，由投影梯度曲线的两个峰值所对应的位置计算出槽型物体宽度等于125像素。

图6 槽型物体宽度实验测量结果

使用圆形标定板以及文献［11］所提出的视觉系统自标定方法对光学系统进行标定，标定结果为0.110 mm／像素。于是，该物体宽度等于13.750 mm。另外，使用千分尺对该槽型物体的宽度进行测量，10次测量结果的算术平均值等于13.770 mm。

5 结 论

本文基于方向功率谱与投影梯度理论，提出一种直边缘物体宽度的图像测量法，并对其原理与精度进行详细分析。理论分析结果表明，本文所提方法能够保证1像素的测量精度，且物体长度方向的几何尺寸不影响宽度测量结果。同时，对该方法的测量精度与有效性进行实验验证，实验结果同样表明本方法在测量准确性与可靠性方面具有很好的优势。

［1］ Cheng Zhihui.Research on algorithm of 2－D measurement for geometry rule mechanical parts based on hough transform［D］.Wuhan：Hubei University of Technology，2009：2－4.（in Chinese）程志辉.基于Hough变换的几何规则零件二维尺寸测量的算法研究［D］.武汉：湖北工业大学，2009：2－4.

［2］ Chen Xiangwei，Wang Longshan，Liu Qingmin.Application of CCD image technology on measuring size ofmicro part［J］.Tool technology，2005，39（8）：86－87.（in Chinese）陈相伟，王龙山，刘庆民.图像技术在微小零件几何尺寸测量中的应用［J］.工具技术，2005，39（8）：86－87.

［3］ Zhao Hongliang.Modified hough transform for line detection and location［J］.Laser＆Infrared，2009，39（9）：1009－1011.（in Chinese）赵洪亮.基于Hough变换改进的直线检测与定位［J］.激光与红外，2009，39（9）：1009－1011.

［4］ Zhang Xiaoyu，Wang Changsong，Yue Shifeng.Photoelectric steel plate lengthmeasurementsystem［J］.Metallurgical Industry Automation，2005，38（1）：46－49.（in Chinese）张小宇，王长松，岳士峰.常化炉前钢板光电测长方案［J］.冶金自动化，2005，38（1）：46－49.

［5］ Dai Na.Study on themeasurement of small rules based on machine vision［D］.Wuhan：Hubei University of Technology，2008：1－72.（in Chinese）代娜.基于机器视觉的小型规则零件二维尺寸测量研究［D］.武汉：湖北工业大学，2008：1－72.

［6］ Zhang Wenzeng，Chen Qiang，Du Dong，et al.Gray projecting integral method for line detection［J］.Journal of Tsinghua University，2005，45（11）：1446－1449.（in Chinese）张文增，陈强，都东，等.直线检测的灰度投影积分法［J］.清华大学学报，2005，45（11）：1446－1449.

［7］ Meng Fanwen，Wu Lushen.Study on 2－D Fourier transform based on FTP［J］.Laser＆Infrared，2008，38（9）：956－957.（in Chinese）孟凡文，吴禄慎.基于FTP的二维傅里叶变换的研究［J］.激光与红外，2008，38（9）：956－957.

［8］ Li Jinju，Ma Zhifeng，Wu Qiongzhi，Du Juan.Image denoise based on the stationary wavelet translation with rotation，shift and scale invariance［J］.Laser＆Infrared，2010，40（11）：1264－1265.（in Chinese）李晋炬，马志峰，吴琼之，杜鹃.基于旋转、平移和尺度不变的平稳小波图像去噪［J］.激光与红外，2010，40（11）：1264－1265.

［9］ Gan Houji，Hua Wenshen.Post processing technique for correlation results based on Fourier－polar transformation［J］.Applied Optics，2010，31（6）：939－942.（in Chinese）甘厚吉，华文深.基于傅里叶－极坐标变换的相关结果后处理技术［J］.应用光学，2010，31（6）：939－942.

［10］Ren Linghui，Liu Kai，Zhang Haiyan，et al.Rectangle detection of gray projection integral extreme value method［J］.Computer Engineering，2012，38（8）：159－163.（in Chinese）任玲辉，刘凯，张海燕，等.灰度投影积分极值法的矩形检测［J］.计算机工程，2012，38（8）：159－163.

［11］Song Xuhui，Zhao Hui，Liu Weiwen.New self calibration method in computer visionmeasurement system［J］.Electronic Measurement Technology，2009，34（3）：34－35.（in Chinese）宋旭辉，赵辉，刘伟文.一种新的视觉检测系统自标定方法［J］.电子计量技术，2009，34（3）：34－35.

Imagemeasuring method for w idth of straight-edge object

ZHANG Tie-ying，BAIFu-zhong，SONG Xiao-yan，WU Jian-xin，GAN Shi-ming
（College of Mechanical Engineering，Inner Mongolia University of Technology，Hohhot010051，China）

A method tomeasure the width of straight－edge object is presented，which is based on directional power spectrum and projection gradient.The directional power spectrum is obtained through polar transformation to power spectrum of the target image，and thus the extending direction of the straight－edge object is calculated.Then the gray projection of the original image is executed along the extending direction，and thewidth value is obtained according to the projection gradient.The proposed method does not require some preprocessing operations such as edge detection and threshold segmentation，and hence itsmeasuring result ismore accurate and reliable.In addition，the proposed method holds low calculation and high measuring efficiency.The results of numerical simulation and experiment show that the proposedmethod can ensure themeasurement precision with one pixel and the length dimension of the object to bemeasured has no effect on the width measuring result.

width measurement；directional power spectrum；projection gradient

TP391.41

A

10.3969／j.issn.1001-5078.2014.02.0

1001-5078（2014）02-0222-05

国家自然科学基金（No.61108038）；内蒙古自然科学基金（No.2011BW0701）；教育部“春晖计划”科研项目（No.Z2011069）资助。

张铁英（1989－），女，硕士研究生，主要从事机器视觉及信号处理方面的研究。E-mail：zhangtieying52＠126.com

2013-09-23；

2013-10-17