人工鱼群算法在基因调控网络中的应用研究
2014-06-07田旺兰李加升
田旺兰,李加升
(湖南城市学院通信与电子工程学院,湖南益阳413000)
人工鱼群算法在基因调控网络中的应用研究
田旺兰,李加升
(湖南城市学院通信与电子工程学院,湖南益阳413000)
在分析基因调控网络现状及优缺点的基础上,提出利用人工鱼群算法对阈值布尔网络模型构建下的基因调控网络进行研究。将阈值布尔网络模型应用于花发育形态模型,构建基于预定义吸引子和极限环的综合网络。比较人工鱼群算法与模拟退火算法在基因调控网络中的应用情况,分析网络节点更新机制变化时布尔网络保留吸引子的能力,发现在极限环长度为2和特定网络拓扑下网络才具有鲁棒性。实验结果表明,与模拟退火算法相比,人工鱼群算法在网络发现、鲁棒性方面具有更好的性能,因此利用人工鱼群算法学习布尔网络结构是有效可行的。关键词:人工鱼群算法;模拟退火算法;布尔网络;吸引子;极限环;花发育形态模型
1 概述
近年来,基因调控网络 (Gene Regulatory Network,GRN)已经引起了机器学习界的广泛关注。研究人员对GRN的不同数学模型进行了研究,分别提出了布尔网络[1]、概率布尔网络[2]、Petri网[3]、贝叶斯网络[4]、递归神经网络[5]等。文献[6]利用蜂群算法(Bees Algorithm,BA)、文献[7-10]利用模拟退火(Simulated Annealing,SA)分别从不同方面对GRN进行了研究,证明了利用群体智能算法研究GRN的可行性,同时表明算法的网络发现频率和网络节点更新序列数量之间存在幂律关系,但是网络发现率不太高、鲁棒性不太好。
人工鱼群算法[11](Artificial Fish Swarm Algorithm,AFSA)是一种较新的群体智能优化算法,文献[12]等提出了一种双域模型人工鱼群算法;文献[13]等用人工鱼群算法对支持型QoS单播路由机制进行了研究,另有学者从不同方面对人工鱼群算法进行了优化和改进,如文献[14]借鉴模拟退火算法中的Metropolis判别准则和利用模拟退火算子改进了人工鱼群的觅食行为,提出了利用模拟退火算法来改进的人工鱼群算法;文献[15]提出了利用高斯变异算子加差分进化变异算子的改进人工鱼群算法;文献[16]提出了基于遗传算法的人工鱼群优化算法,但目前无人将人工鱼群算法用于研究GRN网络。
目前,GRN构建中具有代表性的布尔网络已经广泛应用于酵母细胞周期表达、果蝇体节极性网络、哺乳动物细胞周期表达、花发育形态表达等不同生物的基因调控网络的研究[17]中。本文将人工鱼群算法应用到阈值布尔网络构建的花发育形态模型中,可获得较好的鲁棒性和网络发现频率。
2 人工鱼群算法
2.1 布尔网络
1969年,Kauffuman[1]提出了著名的布尔网络模型,用于研究基因调控网络和细胞分化过程。
设A为关于n的有限集,A={a1,a2,…,an},ai属于{0,1},i=1,2,…,n。一个布尔网络就是一个(G,F)对,这里G=(V,E)为有限有向图,V是n个节点的集合,E是边的集合。F是布尔函数,F:{0,1}n({0,1}由n个局部函数fi:{0,1}n组成,且每个局部函数仅依赖属于邻域Vi={j∈V|(j,i)∈E}的变量。
节点定期更新,根据网络收敛的动力学特性,吸引子分为固定吸引子和极限环,定义为:
固定吸引子:

极限环:

其中,p为极限环,是大于等于1的正整数。
因此,每个节点在t+1时刻的状态可以写为:

其中,wji∈{-1,0,1},是从节点j到节点i的权值,对于所有的节点i,θi=0。这种模型就叫做阈值布尔网络。
对于用阈值布尔网络构建的基因调控网络的边和权值,需要用到一个邻接矩阵M,边表示基因间的相互作用,权值表示基因间的激励或抑制关系。初始矩阵Mi,i=1,2,…,ns在人工鱼群算法里是随机生成的,如图1所示,但该矩阵严格服从节点入度R等的约束。

图1 随机初始矩阵M及其对应布尔网络
网络初始化后,网络节点的更新有很多种方法,人们最感兴趣的有以下2种[6]:
(1)并行或同步模式:每个节点同时更新。
(2)串行模式:在每个时间步长节点按预定义顺序更新。
2.2 算法介绍
2.2.1 适应度函数的定义
布尔网络B的适应度函数即为人工鱼群算法的食物浓度,定义为为每个节点i的网络输出oi和每个节点i的目标值ci间的方差,计算公式为:
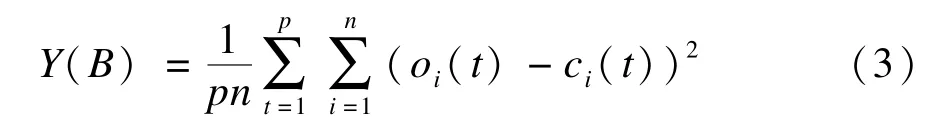
其中,n为网络节点个数;p为吸引子环长度。
2.2.2 人工鱼群算法及算法步骤
人工鱼群算法作为一种有效的智能群体寻优算法,通过模拟鱼类的觅食、聚群、追尾和随机等行为在搜索域内进行寻优,是利用群体智能思想解决优化问题的一个具体应用。
如图2所示,用Pcurr表示人工鱼虚拟实体的当前位置,Visual为其视野范围,Pvisu为其在某时刻的视点所在位置,如果该位置的食物浓度优于当前位置,则可往该方向游进Step,即到达Pnext,Step为其可移动的最大步长。如果位置Pvisu不比当前位置Pcurr更优,则继续巡视视野内的其他位置。巡视次数越多,则对视野内的状态了解越全面,从而对周围的环境有一个全方位的立体认知,这有助于人工鱼群做出相应的判断和决策[18]。Pn1,Pn2,Pn3为视野范围内鱼的位置。

图2 人工鱼的视野域和最大移动步长
位置Pcurr=(p1,p2,…,pn),位置Pvisu=(,,…,),则从Pcurr到达Pvisu的过程可以表示为:

其中,rand为区间[-1,1]内的随机数。
人工鱼群算法中用到的参数如表1所示。

表1 人工鱼群算法输入输出参数
算法伪代码如下:
输入N,Visual,Step,trynum,λ,maxgen
输出 最优解

2.2.3 模拟退火算法
模拟退火源于固体加热至一定温度呈液态后,接着再对其慢慢冷却、降温到预期稳定状态的过程。后来用于解决可以描述为退火过程的最优化问题,固体状态表示可行的最优解,状态能量表示解的客观函数值,最小能量值就是问题的优化解[7]。为了用退火过程来解决现有问题,给出以下4个定义:
(1)解决方案:同人工鱼群算法。
(2)适应度函数的定义:同人工鱼群算法。
(3)搜索策略:同人工鱼群算法,但模拟退火中m的每次迭代,邻域数ngh的减少遵循下式:

其中,ΔE是当前值与新产生的候选解之差。如果ngh<1,则将ngh置1。
(4)冷却进度表:参考标准几何学冷却规则,温度T为:

其中,λ为冷却率常数,λ<1。本文中温度不会在每次迭代后下降,而是每10次迭代才运用此公式一次。
3 人工鱼群算法在基因调控网络中的应用
人工鱼群算法是一种新的不同于传统优化模式的问题解决办法,它只使用目标函数值,对搜索空间具有一定的自适应能力,算法对初值无要求,系统初始化为一随机解,对各参数的选择也不敏感。而对布尔网络的研究,通常是给出节点的初始化矩阵,然后通过计算节点关联的布尔函数,得出节点间的相互关系,这正好与基因调控网络中基因间的激励与抑制关系相对应,所以将人工鱼群算法用于研究布尔网络构建的基因调控网络是可行的。将人工鱼群算法用于花发育形态模型,该模型由EMF1,TFL1, LEF,AP1,CAL,LUG,UFO,BFU,AG,AP3,PI和SUP等基因组成[19],这12个基因即为网络中的12个节点,也就是人工鱼群算法中的鱼群规模。算法行为如下:
(1)觅食行为
设人工鱼即花发育形态网络中的某节点当前状态值为Pi,在其感知域中随机选择一个状态Pj,食物浓度用Y表示,在最大值问题求解中,若食物浓度Yi<Yj(最小值问题求解中Yi>Yj,与此类似),则向该方向游进一步;否则,再重新随机选择状态Pj,判断是否满足前进条件。如此反复尝试trynum次后,如果仍不满足前进条件,则随机移动一步。觅食过程如图3所示。

图3 觅食行为流程
(2)聚群行为
设人工鱼即花发育形态网络中的某节点当前状态为Pi,搜索当前感知域内(即Di,j<Visual)的伙伴数hf和中心位置Pc,如果Yc/hf>λYi(λ为拥挤度),说明伙伴中心位置的食物浓度较大且不太拥挤,则朝伙伴中心位置方向游进一步;否则执行觅食行为。聚群过程如图4所示。

图4 聚群行为流程
(3)追尾行为
设人工鱼即花发育形态网络中的某节点当前状态为Pi,搜索当前感知域内(即Di,j<Visual)的伙伴数hf和这群伙伴中Yj为最大的伙伴Pj,如Yj/hf>λYi,表明该伙伴Pj的周围不太拥挤,且具有较高的食物浓度,则朝伙伴Pj游进一步;反之执行觅食行为。追尾过程如图5所示。

图5 追尾行为流程
(4)随机行为
随机行为的实现较为简单,就是当某人工鱼即花发育形态网络中的某节点状态在最优值附近徘徊时,在视野范围随机选择一个状态,并向该方向游进,这也就是觅食行为的缺省状态,即Pi的下一个位置Pi|next为:

其中,rand为区间[-1,1]内的随机数;Visual为感知域范围。
在算法实现过程中,设立一个公告板来记录最优的网络节点状态。每次寻优后就将节点自身状态与公告板记录进行比较,若优于公告板,则将公告板记录更新为自身状态。
4 实验与结果分析
布尔网络的状态分为暂态和吸引子,吸引子又分为固定吸引子和极限环,本文从吸引子和极限环2个方面评估运用人工鱼群算法所研究的GRN的性能,同时与模拟退火算法在基因调控网络中的应用进行了比较。
4.1 基于固定吸引子的实验
本文实例中,人工鱼群算法用预定义的固定吸引子来研究阈值布尔网络,用到的6个吸引子数据源于文献[19],分别是(0110 0000 1000,1000 0001 1110,0001 0000 0100,0001 1001 0110,1100 0000 0001,0100 0001 0110)。人工鱼群算法、模拟退火分别运行500次并记下每次运行记录以核实它们是否有能力来研究6个固定吸引子。2个算法的参数是在多次运行后根据网络研究和执行时间的有效性根据经验来确定的。设人工鱼群的规模N=12、每条人工鱼的可视范围Visual=3、最大步长Step=1、每次随机移动可尝试的最大次数trynum=5、拥挤度因子λ=0.65,最大迭代次数maxgen=50,对于模拟退火,m=1000,ngh=11,λ=0.7,初始温度T(0)=100。
用于研究阈值布尔网络的6个吸引子实际由42 bit组成(6个吸引子×7个节点)。人工鱼群算法和模拟退火算法运行500次后的结果如图6所示。从图6可看出,当错误位数分别为1,2,3,4,5时,人工鱼群算法发现网络的频率都明显比模拟退火算法要低。

图6 算法运行500次后的结果
4.2 基于极限环的实验
当一个运行在并行更新模式下的网络更新为串行更新模式时,极限环会发生什么变化,极限环会保留还是会破坏,网络拓扑(入度R)会影响输出,为解答以上问题,所以,本实例主要研究网络的鲁棒性。
给定网络节点数为6,预定义的极限环为p=2, 3,4和5,入度R=1,2,3,4,5和6,式(3)中的候选解输出采用并行更新模式。对每一对(p,R),每个网络都有100个不同的极限环被研究,极限环是随机产生且各不相同的常量。然后,当此能够研究极限环的网络更新模式变为串行时(所有可能状态数为6!=720),能保留极限环的网络就会被记录。人工鱼群算法的参数设置如前,模拟退火的为:m= 500,ngh=5,λ=0.7,初始温度T(0)=100。
4.2.1 极限环为2时的实验
图7为极限环p=2时的结果,P/S表示更新机制由并行变为串行时仍能保留极限环的网络,从图7可看出,当节点入度为3和5时,发现的网络才具有保留极限环的能力。图8为入度为3时利用人工鱼群算法得到的布尔网络,网络在并行更新模式下拥有极限环(100101,011010),并且当它从并行变为串行时,串行更新顺序为6-3-5-1-2-4。图9为入度为5时利用人工鱼群算法得到的布尔网络,网络在并行和串行更新模式下的极限环为(110010,001101),顺序为4-1-6-5-3-2。
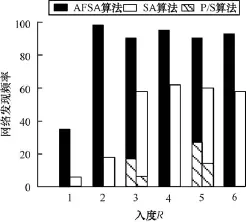
图7 极限环p=2时算法的网络发现频率

图8 R=3时利用人工鱼群算法得到的布尔网络

图9 R=5时利用人工鱼群算法得到的布尔网络
4.2.2 极限环为3,4,5时的实验
为了更进一步说明人工鱼群算法的优越性,以下对极限环p=3,4,5时进行了实验,结果显示,更新模式由并行变为串行时没有网络能保留极限环,结果如图10~图12所示。

图10 极限环p=3时算法发现网络的频率

图11 极限环p=4时算法的网络发现频率

图12 极限环p=5时算法的网络发现频率
综上,由4.1节和4.2节可见,人工鱼群算法在利用预定义吸引子研究阈值布尔网络时要优于模拟退火算法。两者都使用了相同的解决方案、局部搜索策略及适应度函数,而人工鱼群算法得到了显著好的结果。在4.1节中,人工鱼群算法得到的平均入度要低于模拟退火,意味着使用人工鱼群算法比模拟退火仅需较少的边就可以得到更为紧凑的效果。这也表明,利用智能人工鱼群算法搜索解,在每一次迭代中得到的结果比模拟退火方法在每一次迭代时仅用一个候选解要好。
在4.2节中,P/S网络仅出现在p=2时,R=3, 5的情况下,且P/S网络的数量小于网络总数的35%。从图7、图10~图12也可以清楚地看出,随着p的增大,发现网络的频率则减小。当p>2,R= 1时,2种算法都很难发现网络。事实上,当p=3时,模拟退火根本不能发现网络,而人工鱼群算法也仅发现了极少的网络。
5 结束语
本文提出利用人工鱼群算法来研究阈值布尔网络模型构建的GRN,介绍了鱼群算法在基因调控网络中的应用。与模拟退火算法的比较结果表明,鱼群算法利用群体智能算法研究GRN在网络发现和鲁棒性方面具有更好的能力。在以后的研究中,可考虑其他群体智能算法在GRN中的应用,或者改进鱼群算法,因为人工鱼在可见邻域内如果搜索不到比自身状态更优的人工鱼个体,则说明它达到了局部最优值。在觅食行为中,人工鱼会选择随机移动。随机移动的步长大小对最优值的稳定有很大的影响;太大可能会导致人工鱼个体在最优值的附近徘徊,不利于结果的收敛与稳定。为此,可考虑引入随机移动因子来减慢随机移动速度,以得到更快更优的算法。
[1] Kauffman S A.Metabolic Stability and Epigenesist in Randomly Constructed Genetic Nets[J].Journal of Theoretical Biology,1969,22(3):437-467.
[2] Shmulevich I,Dougherty E R.Probabilistic Boolean Networks:The Modeling and Control of Gene Regulatory Networks[M].Philadelphia,USA:SIAMSociety for Industrial and Applied Mathematics,2009.
[3] Steggles L J,Banks R,WipatA.Modelling and Analyzing Genetic Networks:From Boolean Networks to Petri Nets[C]//Proc.of CMSB’06.[S.1.]:IEEE Press,2006:127-141.
[4] Yu J,Smith V A,Wang P P,et al.Advances to Bayesian Network Inference for Generating Causal Networks from Observational Biological Data[J].Bioinformatics,2004, 20(1):3594-3603.
[5] Lee W,Yang K.Applying IntelligentComputing Techniques to Modeling BiologicalNetworksfrom Expression Data[J].Genomics,Proteomics & Bioinformatics,2006,6(2):111-120.
[6] EricGoles G R.LearningGeneRegulatory Networks Using the Bees Algorithm[J].Neural Comput&Applic, 2013,22(1):63-70.
[7] Kirkpatrick S,Gelatt C D,Vecchi M P.Optimization by Simulated Annealing[J].Science,1983,220(4598): 671-680.
[8] Liu G,Feng W,Wang H,et al.Reconstruction of Gene Regulatory Networks Based on Two-stage Bayesian Network Structure Learning Algorithm[J].Journal of Bionic Engineering,2009,6(1):86-92.
[9] Tomshine J,Kaznessis Y N.Optimization of Astochastically Simulated Gene Network Model via Simulate Dannealing [J].Biophys Journal,2006,91(1):3196-3205.
[10] Ruz G A,Goles E.Learning Gene Regulatory Networks with Predefined AttractorsforSequentialUpdating Schemes Using Simulated Annealing[C]//Proceedings of the 9th IEEE International Conference on Machine Learning and Applications.[S.1.]:IEEE Press,2010: 889-894.
[11] 李晓磊.一种新型的智能优化算法——人工鱼群算法[D].杭州:浙江大学,2003.
[12] 马 炫,刘 庆.基于人工鱼群算法的多播树演化寻优[J].通信学报,2012,33(9):1-7.
[13] 王兴伟,秦培玉,黄 敏.基于人工鱼群的ABC支持型QoS单播路由机制[J].计算机学报,2010,33(4): 718-725.
[14] 刘 佳,刘丽娜,李 靖,等.基于模拟退火算法的改进人工鱼群算法研究[J].计算机仿真,2011,28(10): 195-198.
[15] 曲良东,何登旭.混合变异算子的人工鱼群算法[J].计算机工程与应用,2008,44(35):50-52.
[16] 刘 白,周永权.基于遗传算法的人工鱼群优化算法[J].计算机工程与设计,2008,29(22):5827-5829.
[17] 王向红,王 欣,刘莉莉,等.布尔网络动态行为研究[J].浙江师范大学学报:自然科学版,2012,35(1): 47-52.
[18] 王宗利,刘希玉,王文平.一种改进的人工鱼群算法[J].信息技术与信息化,2010,(3):46-49.
[19] Mendoza L,Alvarez-BuyllaE R.Dynamicsofthe Genetic Regulatory Network for Arabidopsis Thaliana Flower Morphogenesis[J].JournalofTheoretical Biology,1998,193(2):307-319.
编辑 索书志
Research on Application of Artificial Fish Swarm Algorithm in Gene Regulatory Network
TIAN Wang-lan,LI Jia-sheng
(College of Communication and Electronic Engineering,Hunan City University,Yiyang 413000,China)
Based on the analysis of the advantages and disadvantages of the current appliance of swarm intelligence algorithm into Gene Regulatory Network(GRN),this paper studies the gene regulatory network constructed under Boolean network model using Artificial Fish Swarm Algorithm(AFSA).Especially,the comprehensive network of predefined attractors and limit cycle is formulated by applying Boolean network model into flower growth morphogenesis. After comparing AFSA with Simulated Annealing(SA)and analyzing the ability of the networks to preserve the attractors when the updating schemes is changed from parallel to sequential,the paper finds the network has robustness within the limit cycle length equal to two and specific network topologies.Experimental results show that the intelligence algorithm outperforms simulated annealing in network discovery and robustness.Therefore,it is feasible to learn Boolean network using AFSA.
Artificial Fish Swarm Algorithm(AFSA);Simulated Annealing(SA)algorithm;Boolean network;
1000-3428(2014)10-0204-06
A
TP18
10.3969/j.issn.1000-3428.2014.10.038
湖南省科技计划基金资助项目(2012FJ3025)。
田旺兰(1977-),女,讲师、硕士,主研方向:网络通信;李加升,教授。
2014-03-20
2014-06-20E-mail:angletw@sohu.com
中文引用格式:田旺兰,李加升.人工鱼群算法在基因调控网络中的应用研究[J].计算机工程,2014,40(10):204-209.
英文引用格式:Tian Wanglan,Li Jiasheng.Research on Application of Artificial Fish Swarm Algorithm in Gene Regulatory Network[J].Computer Engineering,2014,40(10):204-209.
attractor;limit circle;flower growth morphogenesis model
