基于PCA的高维多目标优化可视化方法

刘 广,陈自郁

(重庆大学计算机学院,重庆400044)

基于PCA的高维多目标优化可视化方法

刘 广,陈自郁

(重庆大学计算机学院,重庆400044)

高维多目标优化问题的高维解集由于目标和解的个数众多,对其可视化较为困难。针对上述问题,结合降维和非降维数据分析技术,提出一种高维多目标优化的可视化方法。该方法对高维多目标算法运行后的一组解集进行预处理,运用主成分分析方法分析数据特征,获取转换后的数据及其对应的贡献率。按照贡献率由大到小的顺序调整转换后的数据列顺序;利用主成分贡献率求解转换后数据的行间距离,运行分级聚类算法并对转换后的数据按行排序,重新组织数据,将最终的结果用热图显示。实验结果表明,该方法既能使用户明确转换后每个目标所占的贡献率,又能取得较满意的视觉效果,便于用户理解数据的整体分布并做出决策。

主成分分析;热图;高维多目标优化;可视化;分级聚类;降维

1 概述

多目标优化问题是使多个目标在给定的区域内尽可能达到最佳的优化问题,其在工程应用等非常复杂的实际问题中的应用非常普遍,因此解决多目标优化问题具有重要的实际和科研价值[1]。

当多目标优化问题的目标个数少于3个时,已经有一系列非常有效且成熟的多目标优化算法。当多目标的个数增加到4个及以上时,通常被称为高维多目标优化问题,目标个数的增加对多目标优化算法带来了极大的困难。主要表现在:(1)目标个数的增加使得种群中非支配解的个数指数级增加,极大地削弱了基于Pareto支配进行排序与选择的效果[2];(2)增加了多目标算法的计算复杂度和难度; (3)高维多目标的最优解集为其可视化制造了困难,影响决策者的最终决策。

对于高维多目标的可视化问题,由于人类认知能力的局限性,不能直接观察出来数据之间的冲突和冗余信息,因此需要采用可视化技术,找出数据之间的关系及特征,并对其进行显示。可视化技术为决策者观察分析和理解数据及做出最终的决策,提供了极大的方便。高维多目标可视化技术分为两部分:数据分析和数据显示。

数据显示是指根据数据分析后的结果,采用合适的显示工具,将数据呈现给决策者。目前数据显示的工具非常多,如热图[3]、平行坐标系[4-7]、面向像素技术、Chernoff-face图标显示技术等。其中,平行坐标系方法简单易用,对较少数据,效果较好,但当数据量大、数据维度很高时,会使折线重叠,影响显示效果,干扰决策者的决策。

相比之下,热图的显示方式,直观准确,显示的数据量大,但显示的效果要依赖于事先对数据的良好组织。而面向像素的技术将每一个数据项的数值对应于一个带颜色的屏幕像素,每个属性的所有数据在一个独立的窗口显示。与热图类似,其主要问题是在屏幕上怎样排列这些像素点。还有一种很独特的显示技术Chernoff-face图标显示技术,将一个数据条(包含所有属性)所有的维映射在一张脸上,脸上每个器官代表每个属性,其充分地利用了脸的丰富表情特征,但是能表示的数据集大小却很有限。

数据分析是对数据中的某些特征进行分析和挖掘,找出数据间的规律和特征,从而为数据的显示做准备。数据分析方法包括基于降维的数据分析和基于非降维的数据分析。其中,基于降维的数据分析方法通过分析数据之间的特征,将数据从高维降低或者映射到低维,这样既保留数据的主要特征,又能为分析数据和显示数据带来方便。目前基于降维的数据分析方法包括主成分分析(Principal Component Analysis,PCA)、投影寻踪(Project Pursuit,PP)、多维尺度[8](Multi-Dimensional Scaling,MDS)、自组织映射SOM[9](Self-organizing Mapping,SOM)、局部线性嵌入(LLE)以及基于神经网络和基于分形的降维方法等。文献[10]提出一种结合PCA和平行坐标的数据可视化方法,先利用PCA方法对高维数据进行有效的降维处理,将降维后的数据进行平行坐标可视化展示。该方法能有效地揭示高维数据之间的关系。而文献[11]结合SOM的降维映射技术对大数据进行分类,然后利用平行坐标系进行显示,取得了很好的效果。基于降维的数据分析技术,虽然可以保留高维数据的主要特征,降低维度,为数据的显示带来方便,但是会损失部分原有数据所携带的信息,最终的数据准确与否及显示的效果的好坏,与原数据的特点以及选取的降维方法有直接的关系,并且最终会影响决策者的决策。

而基于非降维的数据分析方法则通过分析高维数据的特征如维与维之间的相关度和距离等,并利用这些特征,指导数据的重新组织排列。与基于降维的数据分析方法相比,其最大的区别是基于非降维的数据分析方法只会根据数据本身分析出来的特征,对数据进行重新调整与组织,而不用减少数据的维度,保持原有数据所携带的信息的完整性。文献[12]针对高维多目标优化结果的显示问题,首先将数据序列化,然后采用非降维的数据分析技术,引导数据集的行和列的重新排列组合,将相关度高的行和列放在一起,最后采用热图将最终结果进行显示,取得了很好的显示效果。尽管非降维的数据分析方法有种种优点,但其缺点也是明显的。首先其对于数据的分析不够深入,不能有效挖掘出数据的内在特征。另外,若高维数据中存在冗余数据,其可能会干扰数据的分析,影响数据维之间的相关度和距离等特征。

本文针对数据分析方法的优缺点,提出一种新的结合降维和非降维的可视化方法,即采用基于降维的数据分析方法,获取数据的特征,并以此来引导数据的重新排列和组织,而无需减少数据的维度,损失信息。

2 相关理论

2.1 多目标优化问题

对于一个具有M维目标的最小化函数,可以记为:

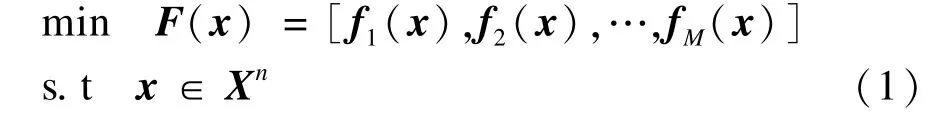
其中,F(x)(x)为M维的目标函数向量;fi(x)为第i维的目标函数;x为n维决策向量;Xn为决策空间,当函数的目标个数M≥4时,称其为高维多目标优化问题。

2.2 主成分分析

主成分分析(PCA)是采取一种数学降维的方法,找出几个综合变量来代替原来众多的变量,使这些综合变量尽可能多地反映原来变量的信息量,而且彼此之间相互独立。通常数学上的处理方法就是将原来的变量做线性组合,适当调整组合系数,使新的变量指标之间相互独立且代表性最好。

对于一组数据矩阵X由M个变量X1,X2,…, XM,Xi=(x1i,x2i,…,xni)T和n个样本组成,其中:

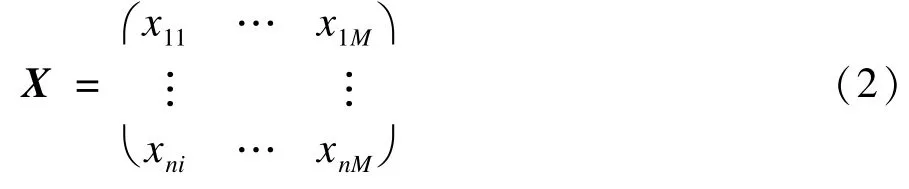
新的综合变量为F,F用以下矩阵表示:

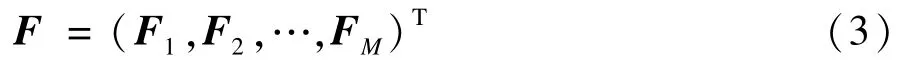
主成分分析就是要找出一个系数矩阵A,A用以下矩阵表示:

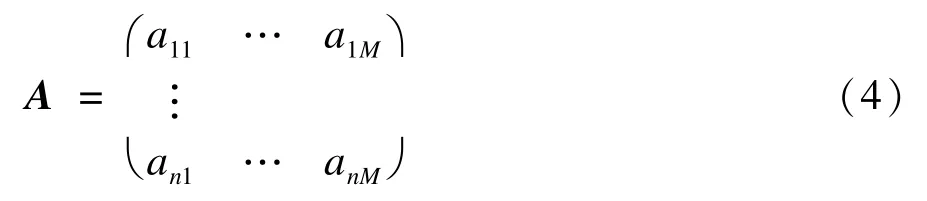
使得F为X中所有列的线性组合:

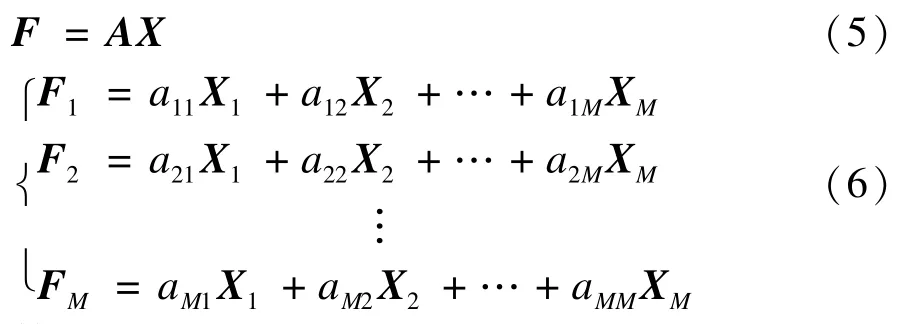
简写为:

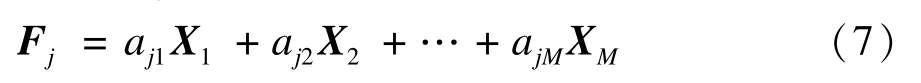
其中,j=1,2,…,M。

系数矩阵由以下原则决定:

(1)Fi,Fj互不相关(i≠j,i,j=1,2,…,M)。

(2)F1,F2,…,FM的方差满足。Var(F1)≥Var(F2)≥…≥Var(FM)。

由以上分析可看出F1,F2,…,FM互不相关,F1的方差Var(F1)最大,则F1包含的信息越多,故称F1为第一主成分,F2为第二主成分,依此类推。可根据实际情况选取F中前几个变量,代替原来所有的变量。

2.3 热图

热图是一种常见的可视化方法,其可以将多维的数据以二维的方式完全直观地呈现出来,并用颜色深浅表示数值的大小。对于数据(200行9列),其热图可视化如图1所示,图中行列分别代表数据的行列,每个数据的大小用颜色的深浅表示。与一些降维可视化方法相比,热图可以同时表示大量的数据,而不损失信息。

图1 热图模型

3 基于PCA的热图可视化方法

3.1 基于PCA的热图可视化方法具体步骤

对于高维多目标算法求得的前沿数据集F,表示为如下:

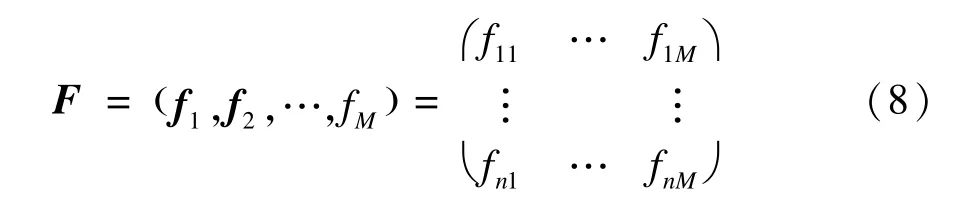
其中,n＞M,n为解的个数,M为目标个数。

本文可视化方法有5个步骤构成:数据预处理→PCA处理→排序→分级聚类→热图显示。

(1)数据预处理

数据标准化预处理。将原数据集F标准化处理,使其变为方差为0,标准差为1的矩阵Z,其计算公式如下:

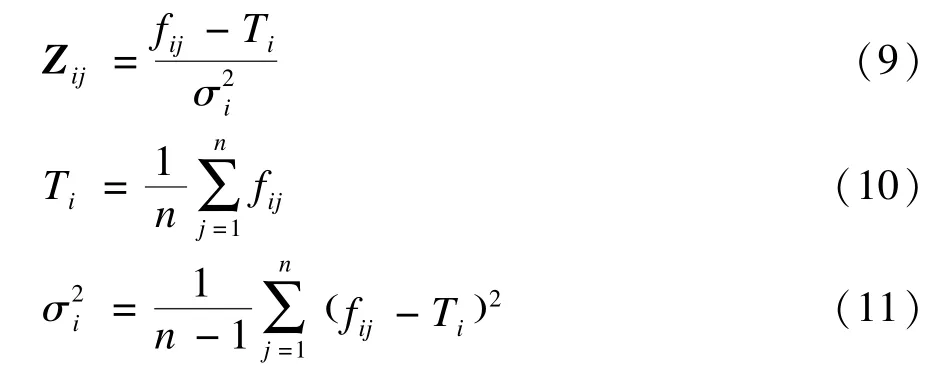
其中,1≤i≤n;1≤j≤M;fij为原数据F中第i行第j列数据;Ti为F中第i行的均值;σi为第i行的标准差。

(2)PCA处理

对于上一步求得矩阵Z,计算相关的协方差矩阵B后,求出协方差矩阵的所有特征值组成的向量A,及其对应的特征向量组成的矩阵C(M行M列),公式如下:

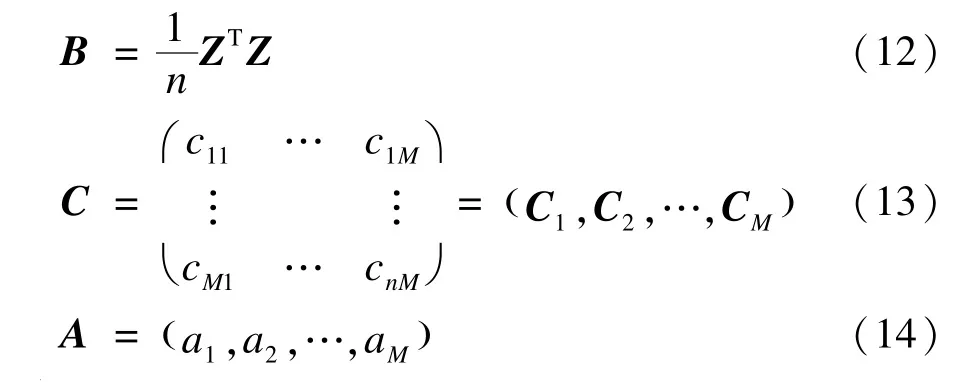
其中,a1,a2,…,aM为协方差的特征值;C1,C2,…,CM为特征值对应的特征向量。

根据特征值,计算转换后的数据矩阵Y,计算方法如下:

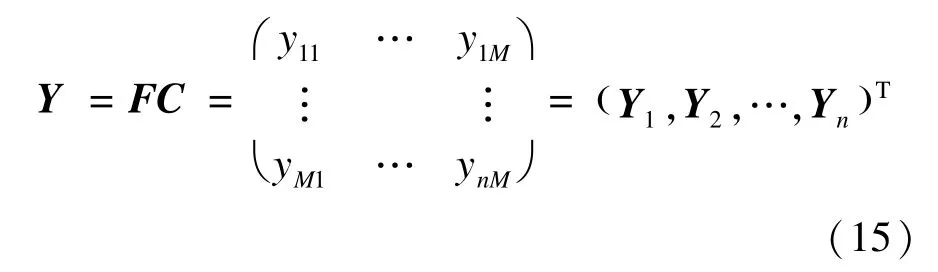
根据式(13)计算出Y中每一列对应的贡献率组成矩阵λ,λ=(λ1,λ2,…,λi,…,λM),其中,1≤i≤M。

(3)排序

对贡献率λi按照从大到小的顺序排列,并相应的调整其对应在Y中列的顺序,假设调整顺序后的矩阵为Y′,其中:

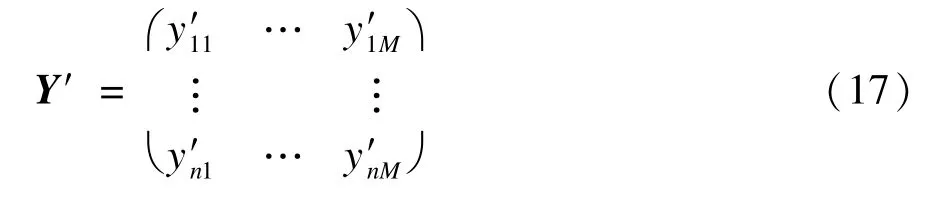
贡献率越大,Y中数据列在Y′中对应的数据列排序越靠前,即此列主成分所占比重越大,在热图中显示顺序越靠前。

(4)分级聚类

为达到满意的可视化效果,还需要对Y′继续处理,即按行间的相似度,进行重新移动排序,重新组织行的顺序,将相关度大的行尽量挪到一起,方便决策者的同时,达到最好的显示效果。

在本文中,将采用分级聚类算法[13],对Y′进行处理。由于此时采用的分级聚类算法是根据距离来判断数据之间的相近度,因此对距离计算方法加以改进,在计算距离时加入了主成分贡献率因素,具体如下:

对于由式(17)得到的数据矩阵Y′,由式(16)可知,Y′每一列的权重大小也就是其贡献率,为λ= (λ1,λ2,…,λM),首先Y′每一列与对应的贡献率相乘,得:

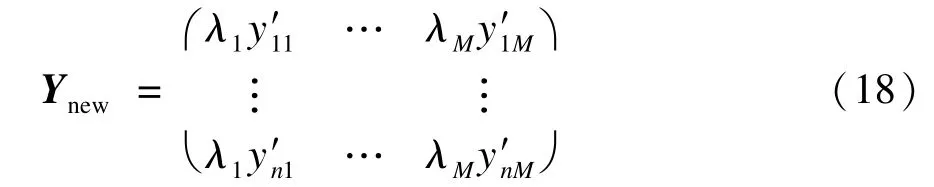
利用以下公式计算λnew中任意两行i,j之间的距离:

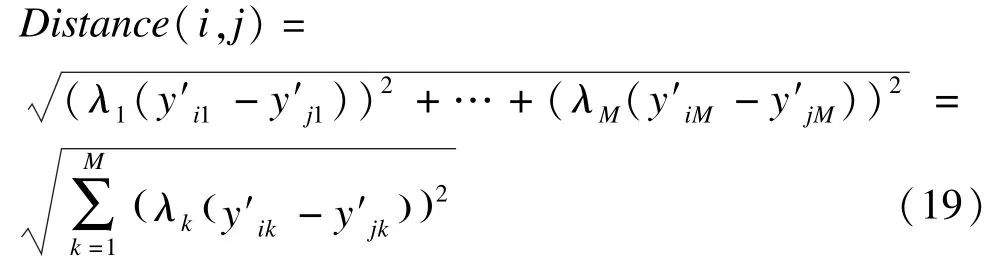
最后分级聚类算法以公式计算行之间的距离,来判断数据间的相似度,设经过处理后得到的数据为Y",Y"也是n行M列的矩阵。

(5)热图显示

经过以上处理后,利用热图对最终得到的结果Y"进行显示。

3.2 方法证明

由以上步骤可知,热图最终显示的是经过处理后的数据,而不是原始数据。原数据经过PCA处理后得到转换后的数据,利用分级聚类算法对转换后数据的所有行进行计算时,采用了基于贡献率的距离计算方法。那么加入了贡献率因素相比于没有加入贡献率因素的距离计算方法,分级聚类结果是否受到影响,从而影响最终的显示效果。

以上过程相当于已知原数据F,经PCA处理转换后的数据为Y,转换矩阵为C,Y中每一列对应的贡献率组成向量λ,λ=(λ1,λ2,…,λi,…,λM),证明加入贡献率因素,即λ中每一个值作为对应Y中每一列的权重,然后计算每列之间的距离,此距离与不加贡献率因素相比,对分级聚类算法处理没有影响,对最终热图显示结果没有影响。

证明如下:

根据式(15)可知,PCA处理转换后的数据为Y,计算公式如下:

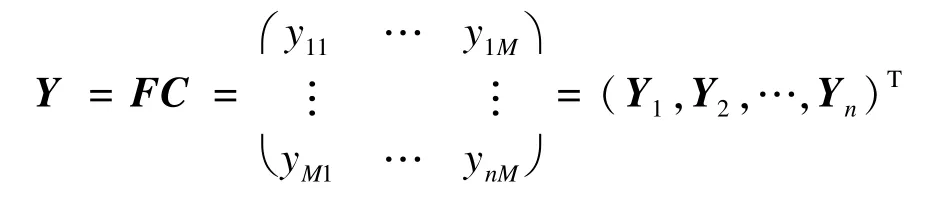
由式(13)可求出C-1=(C1,C2,…,CM),则原数据F满足:

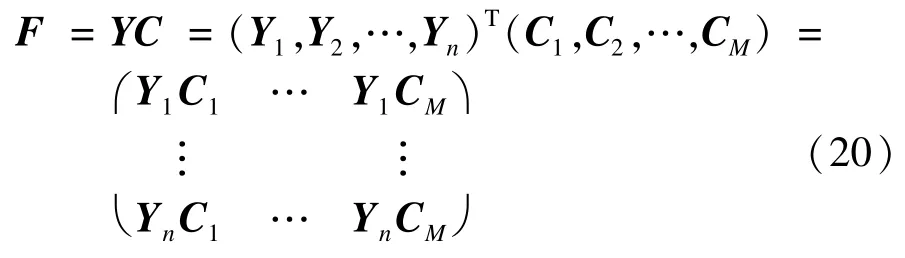
加入贡献率因素λ=(λ1,λ2,…,λM),F中每一列与相应的贡献率相乘,得到新的数据Fnew。

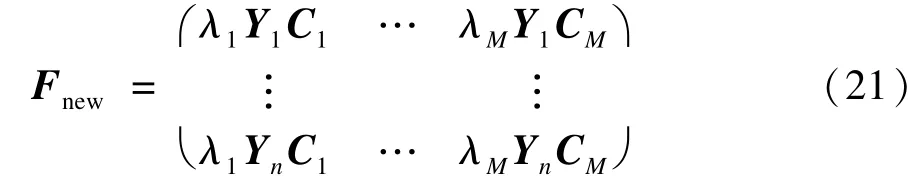
任意两行i与j的距离Distance(i,j)为:

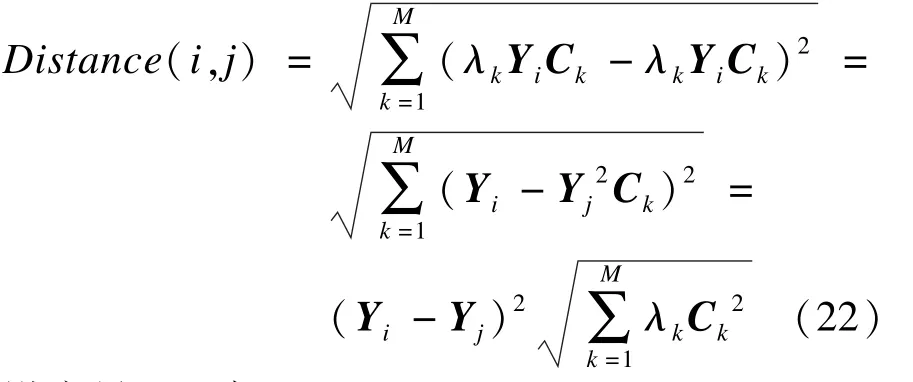
设变量H,则:

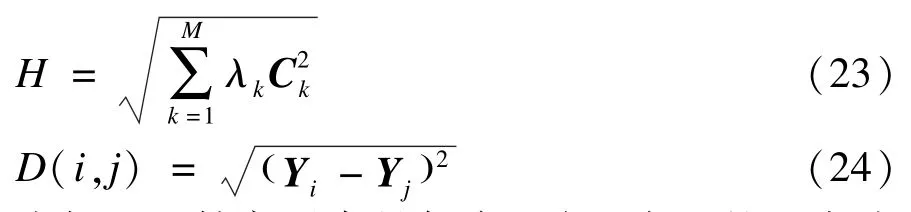
未加入贡献率因素是任意两行i与j的距离为D(i,j):

则最终加入贡献率因素的距离公式可写为:

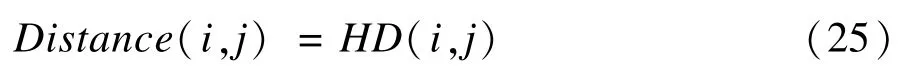
由式(24)和式(25)可知,加入贡献率因素转换后数据行之间的距离相比于不加贡献率因素数据行之间的距离,其只跟常数因素H有关。它们之间的距离会按照相同的比例H增大或缩小,并不会对分级聚类算法判断距离产生影响,对最终的热图显示效果没有影响,原命题得到证明。

4 实验结果与分析

分别利用6目标和8目标的DTLZ2问题,得到2组高维解集,其中,DTLZ2_6D数据由254个解、6个目标组成,DTLZ2_8D数据由380样本、8个目标组成。

对于原始数据DTLZ2_6D,由图2处理过程中得到的3张热图的变化(图2(a)→图2(b)→图2(c))可知:(1)原始数据在未经处理,在热图中显示效果不理想如图2(a),只能知道数值大小,不能有效获知数据之间的关系;(2)经PCA处理后,能得到转换后的数据,和对应的贡献率表,如表1所示。此时得到的热图图2(b)相比于热图图2(a),在整体显示效果上相当,但通过图2(b)能直接获知转换后每个目标的贡献率;(3)数据在经过改进的分级聚类算法处理后,得到最终显示图2(c)。图2(c)相比图2(b),改变了数据行之间的顺序,其显示效果得到极大的提高,在列的维度上,知道每个目标的的主成分的贡献程度,在行的维度上,知道解的相近程度,彼此越靠近,反映在如图上就是一大片色块颜色越相近;(4)用户在最终的图上能方便地挑选需要的解,作出最终决策。如果要求第3目标数值较大,而其他尽量小,则可以在图2(c)中选择第2列最靠下位置的几组解。

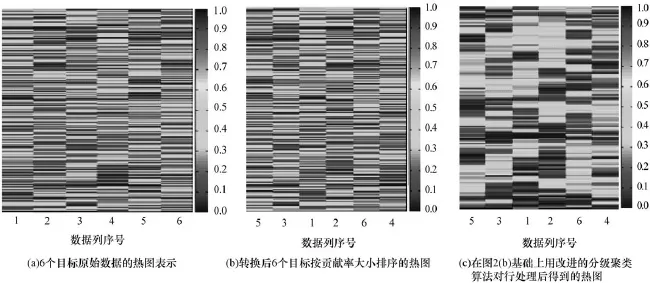
图2 热图变化1

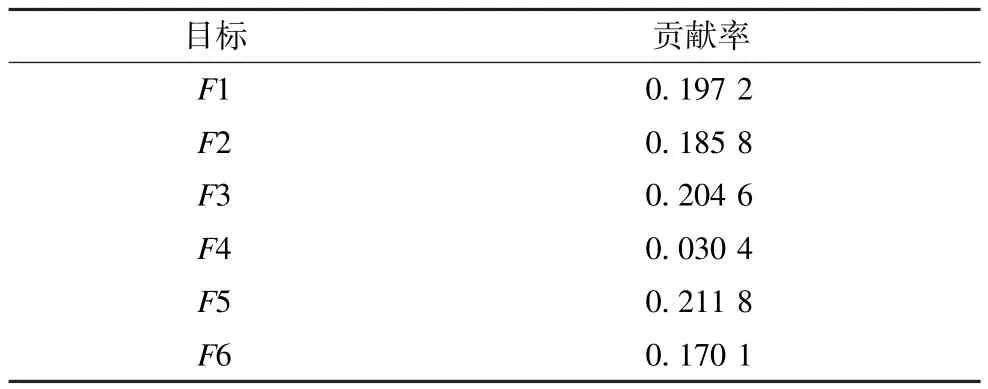
表1 DTLZ2_6D 6个目标对应的贡献率

而对于原始DTLZ2_8D,经过与DTLZ2_6D相同的处理,也得到3张热图和一个贡献率表。从图3的变化过程图3(a)→图3(b)→图3(c),也可与DTLZ2_6D得到类似的结论,显示效果逐渐提高,热图提供的信息递增。从最终结果能够直观地获取目标的贡献率,解之间的相关度,方便用户挑选满意的解。DTLZ2_8D 8个目标对应的贡献率如表2所示。

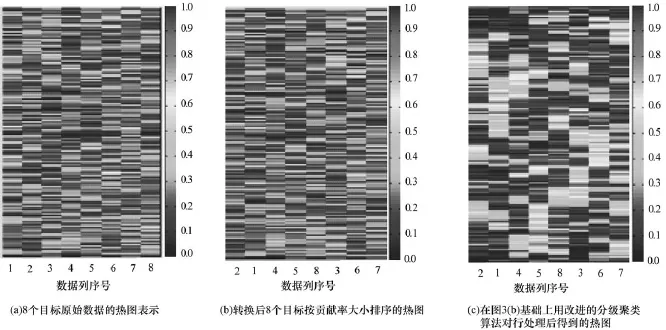
图3 热图变化2

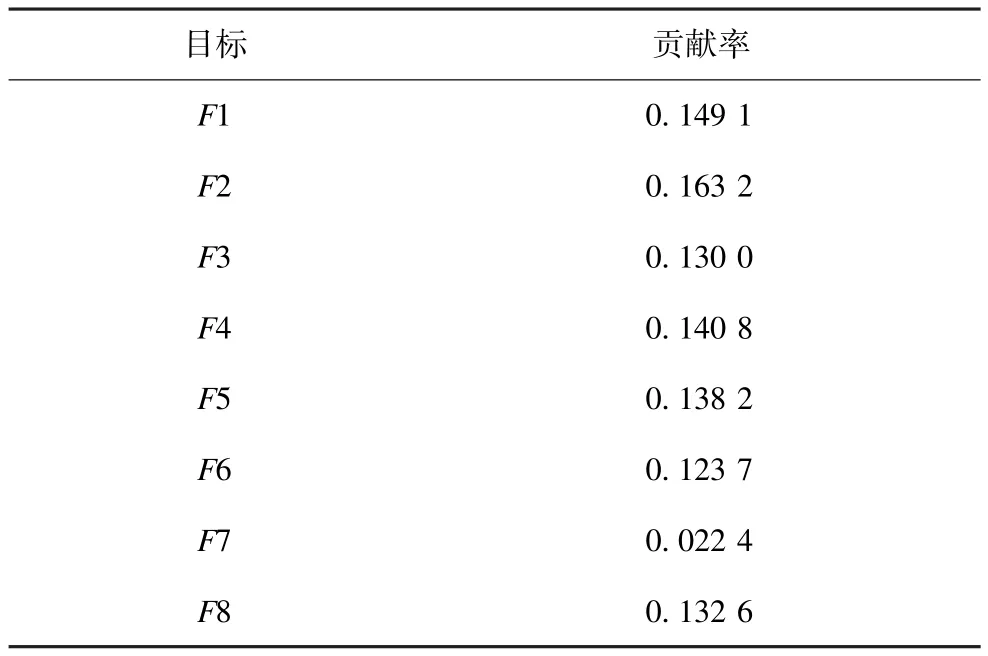
表2 DTLZ2_8D 8个目标对应的贡献率

从以上2组实验可以看出,本文提出的可视化方法既能使用户知道转换后每个目标所占的贡献率,又能取得较满意的视觉效果,方便用户理解数据的整体分布并作出决策。

5 结束语

本文结合基于降维和非降维的数据分析技术,提出一种新的高维多目标优化的可视化方法。该方法能够有效地揭示数据特征,且获得较好的显示效果,最终能够快速地帮助决策者进行决策。然而当高维多目标优化解集中目标之间相关性较差或彼此独立时,该方法不能取得较满意效果。今后的研究将继续完善该方法,针对拥有独特特征的高维多目标优化解集采用不同的数据分析方法和显示工具,并且改进分级聚类算法,优化显示效果,从而更加方便有效地帮助决策者分析和理解数据并进行最终的决策。

[1] 苏勇彦.单目标、多目标优化进化算法及其应用[D].武汉:武汉理工大学,2007.

[2] 孔维健,丁进良,柴天佑.高维多目标优化问题的研究概述[J].控制与决策,2010,25(3):321-326.

[3] Pryke A,Mostaghim S,Nazemi A.Heatmap Visualization of Population Based Multi Objective Algorithms[C]// Proc.of EMO’06.Matsushima,Japan:[s.n.],2006: 361-375.

[4] Xu Yonghong,Hong Wenxue,Chen Na,et al.Parallel Filter:A Visual Classifier Based on Parallel Coordinates and Multivariate Data Analysis[C]//Proc.of International Conferenceon IntelligentComputing.Qingdao,China: [s.n.]:2007:1172-1183.

[5] 洪文学.基于多元统计图表示原理的信息融合和模式识别技术[M].北京:国防工业出版社,2008.

[6] Inselberg A,Dimsdale B.Parallel Coordinates:A Tool for Visualizing Multi-dimensionalGeometry[C]// Proc.of the 1st IEEE Conference on Visualization.San Francisco,USA:[s.n.],1990:361-371.

[7] Johansson J, Treloar R, Jern M.Integration of Unsupervised Clustering, Interaction and Parallel Coordinates for the Exploration of Large Multivariate Data[C]//Proc.of IEEE Symposium on Information Visualization.[S.1.]:IEEE Press,2004:215-222.

[8] Gabriel T R.Rule Visualization Based on Multidimensional Scaling[C]//Proc.of IEEE International Conferenceon Fuzzy Systems.Vancouver,Canada: IEEE Press,2006:333-345.

[9] Kohonen T.Self-organising Maps[M].Berlin,Germany: Springer,1995.

[10] 雷君虎,杨家红,钟坚成,等.基于PCA和平行坐标的高维数据可视化[J].计算机工程,2011,37(1): 48-50.

[11] Fonseca C M,Fleming P J.Genetic Algorithmsfor Multiobjective Optimization:Formulation,Discussion and Generalization[C]//Proc.of the 5th International Conference on Genetic Algorithms.[S.1.]:Morgan Kauffman Press,1993:416-423.

[12] Walker D J,VersonR M,JonathanE.Visualizing Mutually Nondominating Solution Sets in Manyobjective Optimization[J].IEEE Transactionson Evolutionary Computation,2013,17(2):165-184.

[13] 段明秀.层次聚类算法的研究及应用[D].长沙:中南大学,2009.

编辑 索书志

Visualization Method of High Dimensional Multi-objective Optimization Based on Principal Component Analysis

LIU Guang,CHEN Zi-yu
(College of Computer Science,Chongqing University,Chongqing 400044,China)

It is very difficult to visualize the high dimensional solution set of the multi-objective optimization problem for its large number of objective and solution.To solve the above problems,this paper proposes a new method to visualize the high dimensional solution sets with dimensionality reduction and non-dimensionality reduction techniques of data analysis.This method pretreats the solution set of the multi-objective optimization algorithm,uses Principal Component Analysis(PCA)to analyze the characteristics of the data and get the converted data and its corresponding contribution rate.According to the contribution rate order,it adjusts the the order of columns of the converted data,and calculates the distance between the rows of the converted data with the contribution rate use and runs the hierarchical clustering algorithms based on the row distance to reorder the rows and reorganize the data.It displays the result on heat map.Experimental results show that the method can let the user know the contribution rate of the each converted target, offer satisfactory visual effects,facilitate the understanding of the distribution of the data and make decisions.

Principal Component Analysis(PCA);heat map;high dimensional multi-objective optimization; visualization;hierarchical clustering;dimension reduction

1000-3428(2014)10-0192-06

A

TP18

10.3969/j.issn.1000-3428.2014.10.036

刘 广(1987-),男,硕士研究生,主研方向:多目标优化;陈自郁,讲师、博士。

2013-10-14

2013-12-10E-mail:guangliu.123@163.com

中文引用格式:刘 广,陈自郁.基于PCA的高维多目标优化可视化方法[J].计算机工程,2014,40(10):192-197.

英文引用格式:Liu Guang,Chen Ziyu.Visualization Method of High Dimensional Multi-objective Optimization Based on Principal Component Analysis[J].Computer Engineering,2014,40(10):192-197.