求解高维函数优化问题的交叉熵蝙蝠算法

李国成,肖庆宪

(1.上海理工大学管理学院,上海200093;2.皖西学院金融与数学学院,安徽六安237012)

求解高维函数优化问题的交叉熵蝙蝠算法

李国成1,2,肖庆宪1

(1.上海理工大学管理学院,上海200093;2.皖西学院金融与数学学院,安徽六安237012)

为改善蝙蝠算法求解高维函数优化问题的全局搜索能力,提高其搜索精度,将交叉熵方法和蝙蝠算法相结合,提出一种交叉熵蝙蝠算法。该算法将基于重要度抽样和Kullback-Leibler距离的交叉熵全局随机优化算法应用于蝙蝠算法中,采用自适应平滑技术提高算法的收敛速度,利用交叉熵方法的遍历性、自适应性和鲁棒性,有效抑制蝙蝠算法的早熟收敛现象。对经典测试函数和CEC2005测试函数的仿真结果表明,该算法具有全局搜索能力强、求解精度高和鲁棒性好等特性。

高维函数优化;蝙蝠算法;交叉熵;重要度抽样;自适应平滑;协同演化

1 概述

随着科学技术的快速发展,人们在现实世界中面临着更加复杂多变的系统,如电力系统、蛋白质结构、医学图像匹配以及金融市场等。这些复杂系统的模型参数优化问题常常在高维空间进行,具有许多在低维空间里不曾有过的独特现象和困难,进而为优化领域带来了新的挑战。经典优化方法在处理这类问题时随着维数的增加,其表现不尽如意[1-3]。近年来,智能优化算法的兴起与蓬勃发展为这类问题的求解开辟了新途径,如遗传算法(Genetic Algorithms,GA)[4-5]、粒子群优化(Particle Swarm Optimization,PSO)[6-8]、微 分 进 化 (Differential Evolution,DE)[9]和人工蜂群(Artificial Bee Colony, ABC)算法[10-11]等。这些算法在求解高维函数优化问题上取得了一些进展,但其维数上的突破仍然很有限,维数的增加对其求解精度和收敛速度有着非常大的影响,无法彻底解决。

交叉熵[12](Cross-entropy,CE)方法是Rubinstein在研究复杂随机网络中的小概率事件估计问题时提出的一种全局随机优化方法。该方法以统计视角,采用重要度抽样,引入Kullback-Leibler距离来度量2个概率分布的交叉熵并使之最小,用以求解组合优化、稀有事件估计以及机器学习等问题,具有很好的随机性、自适应性和鲁棒性[13],在复杂网络可靠性分析、组合优化以及工程优化设计和控制等方面取得了很好的应用效果[14-15]。文献[16]将该方法应用到多峰值连续函数优化问题,发现函数维数的增加对其求解精度的影响很小,是求解复杂高维优化问题的新途径。但交叉熵方法如同其他Monte Carlo技术一样,存在样本容量大、收敛速度慢等不足。本文将在保持其优良的高维优化问题求解能力的基础上积极探寻与其他启发式算法进行协同演化以提高其收敛速度。文献[17]于2010年基于仿生学提出的一种新型启发式算法——蝙蝠算法(Bat Algorithm,BA),该算法很好地融合了粒子群优化、和声搜索和模拟退火等算法的优点,在多目标优化、工程优化以及生产调度优化等方面取得了很好的应用效果[18-20]。本文将交叉熵随机优化方法嵌入到蝙蝠算法中来构建一种新型启发式搜索算法,称为交叉熵蝙蝠算法(Cross-entropy Bat Algorithm,CEBA)。

2 标准蝙蝠算法和交叉熵优化方法

2.1 蝙蝠算法

蝙蝠算法[17](Bat Algorithm,BA)是 Yang于2010年基于仿生学提出的一种新型启发式算法。该算法通过模拟蝙蝠在复杂环境中搜寻、定位和捕捉猎物的过程进而形成基于群体的仿生算法。在初始化群体中每个个体在搜寻空间中的位置和速度后,其位置和速度迭代更新规则如下:

其中,fi为蝙蝠i的脉冲频率;β∈[0,1]为均匀分布的随机数;和为其t时刻飞行速度和位置;x*为t时刻群体最佳位置。同时,通过模拟蝙蝠在探寻到猎物后通过逐渐减弱脉冲音强、增大脉冲发射次数来实现精度定位猎物过程来进行局部搜索,具体如下:

蝙蝠仿生算法很好地融合了粒子群优化、和声搜索和模拟退火等算法的优点,在工程优化、生产调度和约束优化等问题上取得了很好的应用效果[15-17]。但该算法存在早熟收敛现象,其寻优精度和收敛速度也有待提高。为此,文献[21]采用Lévy飞行策略来改进BA的寻优精度和全局优化性能,文献[22]通过引入混沌Lévy飞行来提高其收敛速度,并改善求解精度;在收敛性和全局优化方面,文献[23]对BA的收敛性进行了研究,文献[24]通过采用正交拉丁方原理生成蝙蝠群的初始空间位置和模拟蝙蝠的追随、自主、避险和从众行为来构造可全局收敛的BA,并应用于复杂函数和高维函数的优化问题,其研究结果表明BA求解高维函数优化问题的计算成本是非常高的,而且精度不高。此外,在离散优化问题上,文献[25-26]分别提出了二进制蝙蝠算法和元胞蝙蝠算法,极大丰富了BA算法及其应用。

2.2 交叉熵随机优化方法

考虑如下最优化问题:

交叉熵算法将其关联到相关的概率估计问题,根据一族定义在X上的概率密度函数{f(·;v),v∈ν}随机化问题式(7),得到其辅助随机问题:

其中,Eu是期望算子;I为示性函数;γ为自适应更新参数。为了减小样本数量,CE采用重要度抽样法,将式(8)转化为:

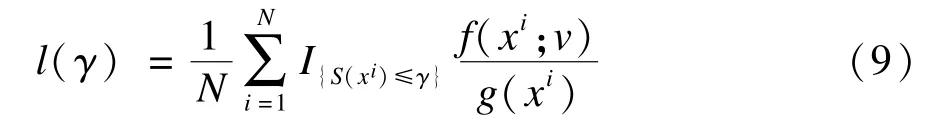
其中,xi为重要度抽样密度g(x)生成的样本。为求得最优的重要度抽样密度,引入Kullback-Leibler距离来度量2个概率分布f(x;v)与g(x)间距离即交叉熵,并最小化交叉熵:

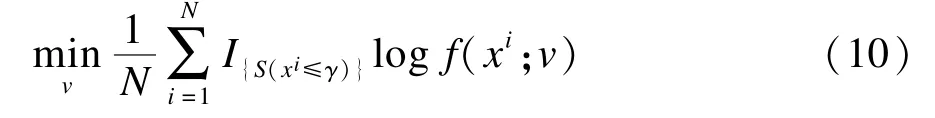
从而得到最优的g*(x)。

CE全局随机优化算法的实施过程为:

Step 1 根据预定义参数的概率密度函数生成候选解集;

Step 2 用引导搜索向全局最优解逼近的精英解集来更新概率密度函数的参数,产生迭代序列,直至满足终止条件。

CE算法具有预定义参数少、迭代操作简单和数值稳定性好等优点,在组合优化和工程优化设计方面有着广泛的应用。

3 交叉熵蝙蝠算法

交叉熵蝙蝠算法是将交叉熵方法嵌入到蝙蝠算法中,通过协同演化共同更新种群,有效增强算法搜索过程中种群的多样性,提高算法的全局优化能力,同时加快了CE中均值和方差的演化速度,降低了抽样成本。

3.1 算法原理

基于模型的交叉熵优化算法的优点在于自适应性和鲁棒性强,具有很好的全局优化能力,不足之处是抽样需要大量样本,计算成本高,收敛速度慢。而源自于仿生学的蝙蝠算法[17]具有很强的局部搜索能力,但也易陷入局部最优解状态,很难得到全局最优解。为此,采用融合技术,将CE嵌入到BA中,形成新的启发式随机搜索算法。新算法CEBA包含BA和CE 2个优化迭代算子,通过协同演化来共同更新种群中每个个体所处的位置,对应着优化问题的候选解,同时又分别利用种群的信息来实现各自迭代过程中相关信息的更新。其中,CE算子利用共同更新后的种群来刷新自己的抽样概率分布的参数,这样利用协同演化的种群来加速CEBA算法的演化进程,大幅减少抽样样本数,进而降低计算成本,同时充分发挥自己的全局优化能力;而BA算子也因协同演化获得更好的个体,极大地丰富了种群的多样性,从而提高了CEBA算法的收敛速度和增强全局优化能力。

3.2 算法步骤和流程描述

基于交叉熵方法和蝙蝠算法所融合而成的新型启发式算法(CEBA)的具体算法步骤如下:

Step 1 确定搜索空间,初始化基本参数。随机生成初始种群。假设在d维搜索空间中,考虑P只蝙蝠,则每只蝙蝠的位置代表优化问题的候选解,初始种群为:

其中,表示初始时刻t=0时蝙蝠i在第n维搜索空间的位置。

Step 2 启动BA优化迭代操作,评估每只蝙蝠的适应度,并更新最优解Xbest和最优值Gbest。

其中,表示蝙蝠i在t时刻的适应度值;fitness(·)为适应度函数,用于评判蝙蝠位置的优劣。

Step 3 按式(1)～式(3)调整每只蝙蝠的频率,更新速度位置和位置。

Step 4 对当前最优解进行扰动操作:若rand1＞ri,则随机游走到某个最优位置的一个紧邻位置;否则保持不动。

Step 5 执行随机飞行操作并按式(4)获得一个新解,若rand2＜ri且f()＜f(x*),接受新解并分别按式(5)和式(6)更新和。

Step 6 启动CE优化迭代操作:

(1)初始化参数,计算种群各维的均值μ^和标准差。

(2)按Y～N(,2)抽取样本Y1,Y2,…,YL。

(3)执行协同演化操作:评估X和Y中所有个体,更新最优解Xbest和最优值Gbest;选取最好的P个个体来更新X及fit,并取其中的最好的Ne个作组成精英群体Xe,计算其均值和标准差。

(4)均值和标准差更新的平滑化,按下式更新抽样概率分布参数:

(5)检查CE迭代终止条件,若满足,则停止CE迭代;否则转向(2)。

Step 7 检查BA迭代终止条件,若满足,则停止,否则转向Step3。

交叉熵蝙蝠算法的流程如图1所示,主要体现在BA和CE的协同演化上,从而在优势互补的同时又强化各自的优势。

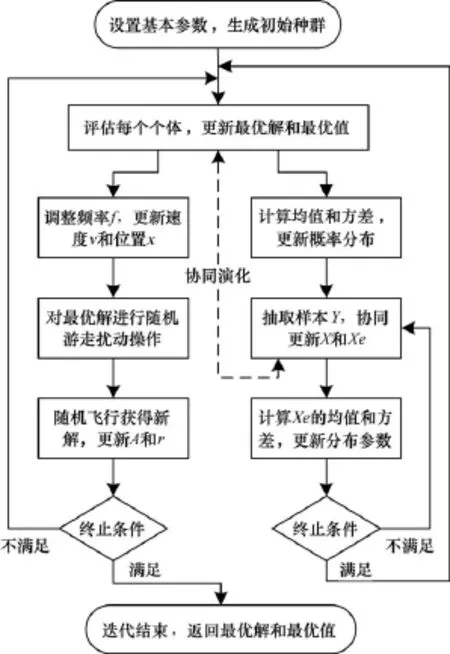
图1 CEBA算法流程

3.3 CEBA算法的优势

如此建立的新型启发式随机搜索算法在局部收敛和全局优化上分别汲取了BA和CE的优势,协同演化的结果不仅促成优势互补,而且增强了各自的优势,形成一些新的特质和优势,具体如下:

(1)寻优精度高、鲁棒性强。基于群体的蝙蝠仿生算法和基于模型的交叉熵全局随机优化算法的有机融合使得新算法在勘探能力和开采能力之间取得了很好的平衡,协同演化技术的应用使得这种平衡得以完美实现,以Schwefel函数(维数为128)为例给出其协同演化过程中最优解的交替更新如图2所示。为BA算子对最优解的更新,其余CE算子为对最优解的更新,可见协同演化技术能被很好地实施,因而新算法具有全局勘探能力强和局部搜索精度高的特质。

图2 协同演化过程中最优解的更新

(2)计算成本低、收敛速度快。相对于BA而言, CE算法参数少,优化过程简单,计算量小;相对于CE算法而言,BA收敛速度过,局部优化能力强。因此将2种算法进行融合既通过BA加快收敛速度、降低CE算法的抽样数,又使得计算成本远小于BA。

(3)适合于求解高维函数优化问题。新算法中的CE具有求解高维函数优化问题的特质,随着解空间维数的增加,其计算成本只涉及概率分布参数中的均值和方差的刷新,不会带来维数灾难,因而适合求解高维函数优化问题,这一点事不同于文献[24]的,而是CE算法的特质。

4 数值仿真

4.1 测试问题与比较对象

为了测试CEBA算法求解高维函数优化问题时的性能,采用与文献[17]相同的标准测试函数及文献[27]提供的经典标准测试函数和文献[28]所提供的CEC2005标准测试函数来进行测试和对比,测试函数的具体描述和特征参见文献[17,27-28]。其中,第1个函数集是用来评估新算法的优化性能,并与标准的BA和CE算法进行对比;第2个函数集是用来对比新算法和经典启发式搜索算法求解连续函数优化问题的优化性能,算法比较对象选取常用的GA和PSO算法;第3个更为复杂的CEC2005函数集是用来验证新算法求解高维函数优化问题的可行性和有效性,本文分别选取文献[23]提出的合作进化策略下自适应邻域搜索微分进化算法(DECC-G)和文献[24]所提出的统计变量互学习策略下的合作粒子群优化算法(CPSO-SL)作为比较对象,具体测试和对比详细情况如表1所示。实验硬件环境为Intel(R)Core (TM)i3 CPU M2.27 GHz,2 GB RAM;软件环境为Windows 7和Matlab 2012b。

表1 测试问题和比较对象

4.2 参数设置与测试结果

测试1的算法相关参数设置为:BA的种群规模为100,其他参数同文献[17];CE样本容量Nc和有效样本数Ne分别为100和30,BA和CE的最大迭代次数为1 550;CEBA中BA算子最大迭代次数为50,其他参数设置同前,其CE算子最大迭代次数为30,其他参数设置同前。3种算法对每个测试函数独立运行25次,每次的函数评价次数均为1.55×105,其测试结果与对比如表2所示,表中第1列为10个测试函数,平均值反映了算法的寻优能力,标准差反映了算法寻优能力的稳定性,其最优值均以粗体标识。

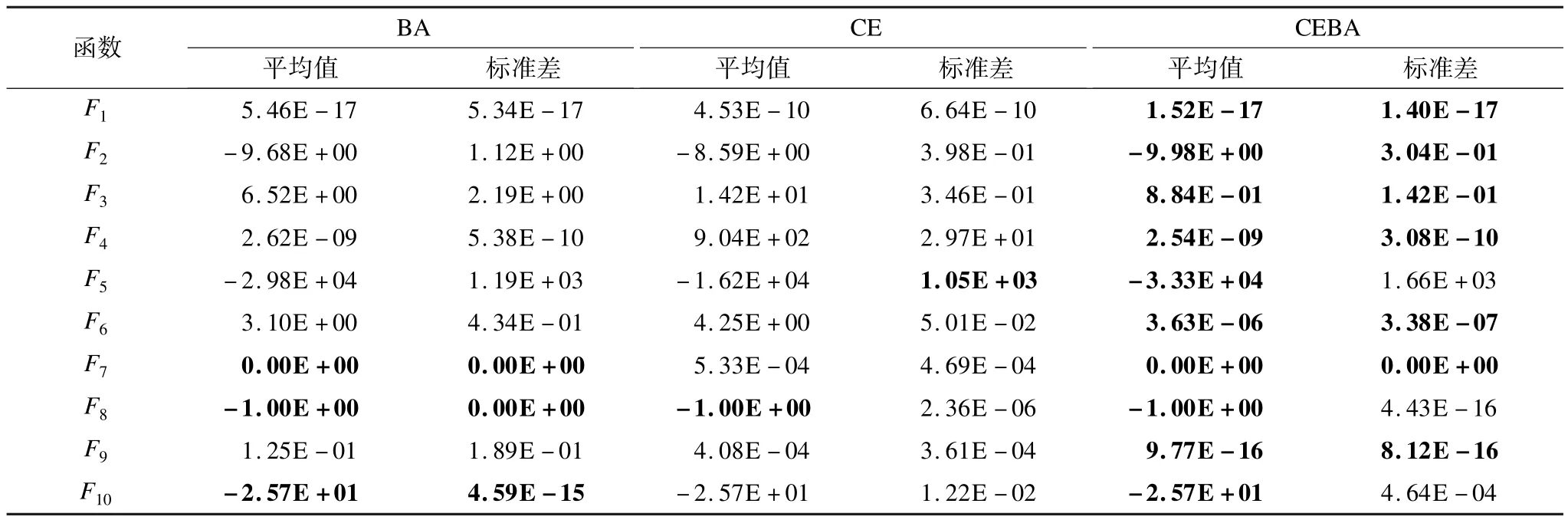
表2 测试1的测试结果与对比

从表2可以看出,与标准的BA相比,在10个测试函数中CEBA胜出7,其余3个寻优结果除在F8和F10的标准差略逊外是一样的;与标准的CE相比, CEBA是完全胜出,即使F8均值是一样,但标准差CEBA算法要好得多。

测试2的算法相关参数设置为:GA和PSO种群规模为100,其中GA的pc和pm分别为0.2和0.8,PSO的加权因子C1=C2=2,加权函数w从0.9线性递减到0.2,最大迭代次数均为1 020,迭代停止标准为达到最大迭代次数;CEBA中BA种群规模为50,最大迭代次数为40,其他参数设置同文献[17]; CE样本容量Nc和有效样本数Ne分别为100和30,最大迭代次数为25。3种算法对每个测试函数独立运行25次,每次的函数评价次数均为1.02×105,测试和对比结果见表3和表4。

测试3中CEBA算法的BA和CE最大迭代次数分别为50和200,其他参数如前文所设,2种维数对应DECC-G算法的函数评价次数分别为2.5×106和5×106;而 CEBA算法的函数评价次数均为1.002 5×106。测试和对比结果如表5所示,为了便于对比,参照文献[29]给出CEBA算法的独立运行25次结果的平均值。

测试4中CEBA算法的BA和CE最大迭代次数分别为50和1 000,其他参数如前文所设;比较对象CPSO-SL的2种维数对应的函数评价次数分别为1.0×108和2.0×108,而CEBA算法的函数评价次数均为5.002 5×106。测试和对比结果如表6所示,为了便于对比,参照文献[30]给出CEBA算法的30次独立运行的平均值。

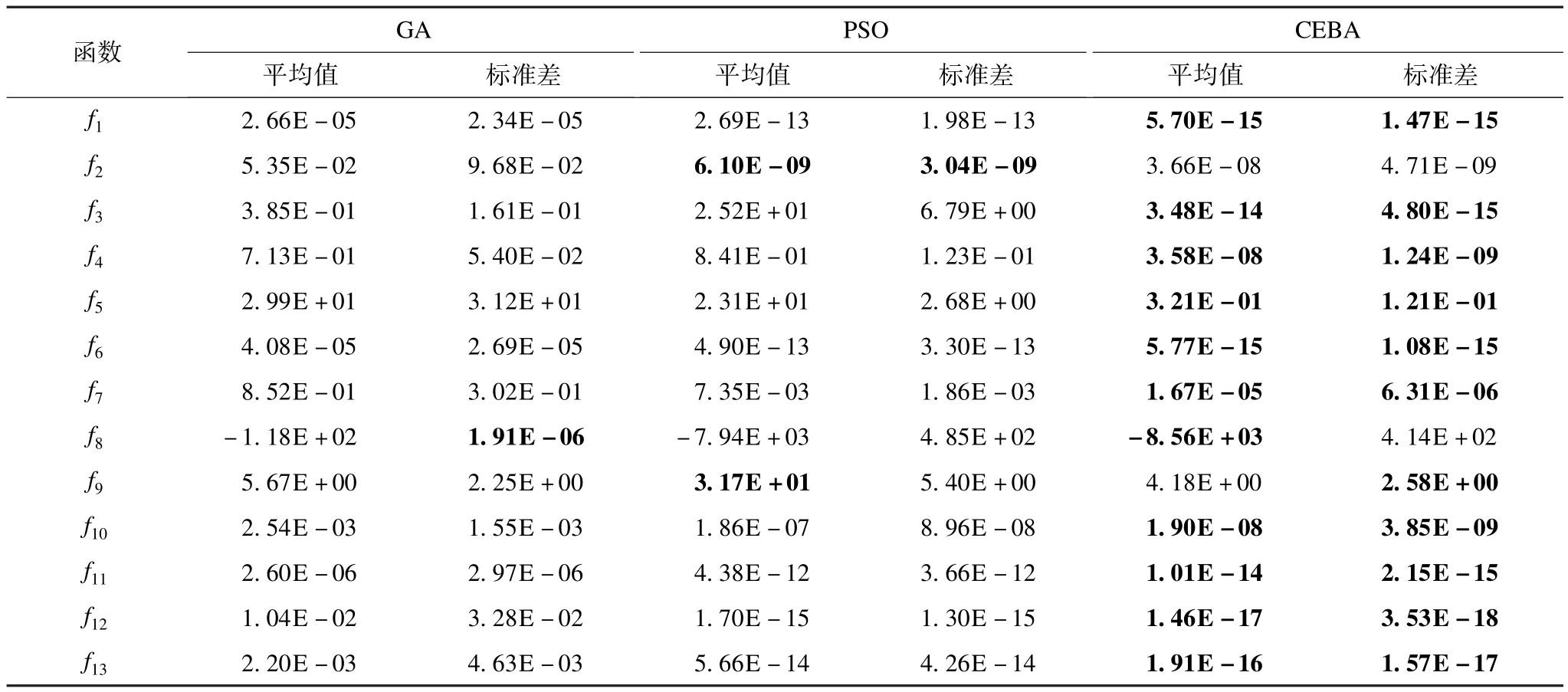
表3 测试2中d=30时的测试结果与对比

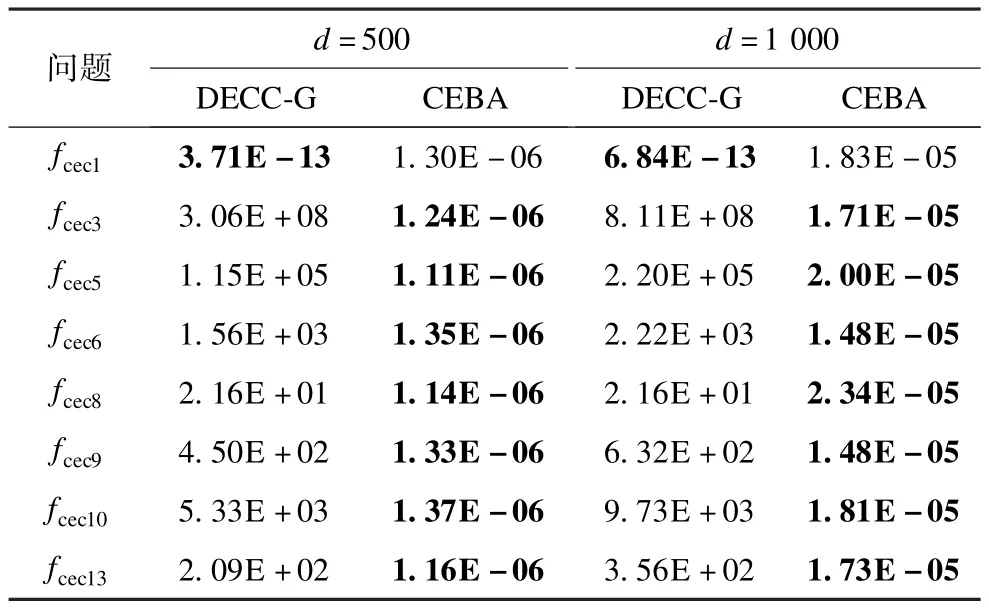
表5 测试3的测试结果与对比

从表3和表4可以看出:(1)13个经典测试函数2种维数取值的测试结果中CEBA算法所求结果中除了d=30时的f2和f9略逊于PSO外全部胜出,表明本文所构建的CEBA算法在求解高维函数优化问题时的表现要明显好于标准的GA和PSO2种算法;(2)CEBA算法的搜索精度是非常高的,标准差都很小,表明该算法稳定性好、鲁棒性强,即使对于非常复杂的函数f5也取得了不错的效果,远好于另外2种算法;(3)随着维数的增加CEBA算法的寻优效能并没有发生明显地减弱,而GA和PSO优化效能却降低很多。

表5中DECC-G算法的求解结果来自文献[23],可以看出除fcec1外,其他7个函数的求解结果CEBA均胜出,而且明显好于DECC-G算法,而2种维数下CEBA的函数评价次数分别不及DECC-G算法的一半和1/4,以很低的求解成本就获得很高的求解精度。

表6中CPSO-SL算法的求解结果来自文献[24],在所测试的10个CEC2005函数中,CEBA有7个胜出,其余3个求解精度略逊于CPSO-SL算法,但也是相当高的,而所有10个函数的求解精度都高于1.0E-09,适用所有10个测试函数,这要明显好于CPSO-SL算法,其优化性能在其中一些函数上表现很好而对另一些的求解结果就远不如CEBA算法。同样求解成本远小于文献[24]。表5和表6都表明CEBA算法收敛速度快,求解精度高,全局优化性能好,具有很好的鲁棒性,其原因在于CEBA算法实现了CE和BA的优势互补,并通过协作演化强化了各自的优势,从而提高了算法的搜索精度,增强了算法的稳定性。

为了研究BA、CE和CEBA3种算法求解精度对维数的敏感性,以Rastrigin函数为例,解空间维数以20为起点、步长为10依次递增到200,如图3给出3种算法25次独立运行求解所得最优函数值的平均值与随维数变化的对应关系与对比,可见CEBA算法的优化效能并不随解空间的维数的增加而发生显著变化,而标准的BA和CE的在求解高维函数优化时(维数大于10),其求解性能就下降很多。此外,在耗时上,CEBA也是最少的。由此可见,改进算法的优化性能的提高是显著的,实际优化效果的改善是明显的。

图3 不同解空间维数下3种算法求解精度对比

为了进一步探讨本文所构建的算法在求解高维函数优化问题时维数的增加对算法寻优效能的影响以及该算法的收敛性征,本文选取标准的 GA和PSO作为比较对象。首先以函数f1为例给出3种算法在解空间维数以10为起始点、步长为10依次递增到200时所求解得到的最优目标函数值变化情况如图4所示。

图4 不同解空间维数下3种算法最优目标函数值变化情况

图4 显示CEBA算法的求解精度随着解空间维数的增加变化不大,表明CEBA算法适合求解高维函数优化问题。维数的增加对算法求解精度影响最大的是PSO算法,维数低于20维时,其求解精度最高,但超过50维时其求解效果很差,GA算法总体上来说,其在求解高维问题时的表现不佳。

其次,以函数f1和f5为例,在d=30时描绘出3种算法的收敛特征曲线如图5和图6所示,其中,x轴为迭代次数n;y轴为每次迭代的最优函数值fmin,且y轴采用对数刻度。

图5 f1的3种算法收敛特征曲线对比

图6 f5的3种算法收敛特征曲线对比

从图5和图6可以看出,CEBA算法的收敛速度明显快于GA和PSO 2种算法,同时其求解精度也是最高的。进一步表明CEBA算法不仅提高搜索精度、增强算法稳定性,同时也改善了算法收敛速度。

5 结束语

针对高维函数优化这一复杂问题,本文构建了一种新的交叉熵蝙蝠协同演化算法,该算法将交叉熵随机优化技术嵌入到蝙蝠算法的迭代过程中,利用交叉熵方法的随机性、自适应性和鲁棒性改善蝙蝠算法的全局寻优能力;同时,利用蝙蝠算法加快交叉熵收敛,实现协同演化,从而保证新算法能快速获得全局最优解。仿真实验结果表明,CEBA与标准的BA和CE算法相比,优化性能得到很大提高,收敛速度更快,求解精度更高,具有比经典的智能算法如GA和PSO更好的寻优性能和稳定性,搜寻精度高和收敛速度快。同时与文献[23]的结果相比较, CEBA求解精度更高且成本更低,与文献[24]的结果相比较,CEBA算法具有更好、更快的全局寻优能力。3个测试和对比结果表明,该算法用于求解复杂的高维函数优化问题是可行性和有效的,即使是超高维问题该算法仍然适用。

[1] Schoen F.GlobalOptimization MethodsforHighdimensionalProblems[J].European Journal of Operational Research,1999,119(2):345-352.

[2] Grosan C,Abraham A.A Novel Global Optimization Technique forHigh DimensionalFunctions[J]. International Journal of Intelligent Systems,2009,24(4): 421-440.

[3] Grosan C,Abraham A,Hassainen A E.A Line Search Approach for High Dimensional Function Optimization [J].Telecommunication Systems,2011,46(3):217-243.

[4] Hedar A,Fouad A.Genetic Algorithm with Population Partitioning and Space Reduction for High Dimensional Problems[C]//Proc.of 2009 International Conference on Computer Engineering and Systems.Cairo,Egypt: IEEE Computer Press,2009:151-156.

[5] 武慧虹,钱淑渠,徐志丹.克隆选择免疫遗传算法对高维0/1背包问题应用[J].计算机应用,2013,33 (3):845-848,870.

[6] Jia D L,Zheng G X,Qu B Y,et al.A Hybrid Particle Swarm Optimization Algorithm for High-dimensional Problems[J].Computers&Industrial Engineering, 2011,61(4):1117-1122.

[7] Martins A A,OluyinkaA A.AnAdaptiveVelocity Particle Swarm Optimization for High-dimensional Function Optimization[C]//Proc.of2013 IEEE Congress on Evolutionary Computation.Cancún,The United States of Mexico:IEEE Computer Press,2013: 2352-2359.

[8] 陈义雄,梁昔明,黄亚飞.一种改进的混沌量子粒子群优化算法[J].计算机工程,2013,39(8):253-256.

[9] Yang Z Y,Tang K,Yao X.Differential Evolution for High-dimensional Function Optimization[C]//Proc.of 2007 IEEE Congress on Evolutionary Computation. Singapore:IEEE Computer Press,2007:3523-3530.

[10] 林志毅,王玲玲.求解高维函数优化问题的混合蜂群算法[J].计算机科学,2013,40(3):279-282.

[11] Ren Y F,Wu Y.An Efficient Algorithm for Highdimensional Function Optimization[J].Soft Computing, 2013,17(6):995-1004.

[12] Rubinstein R Y,Kroese D P.The Cross-entropy Method: A Unified Approach to Combinatorial Optimization, Monte Carlo Simulation and Machine Learning[M]. New York,USA:Springer-Verlag,2004.

[13] Margolin L.On the Convergence of the Cross-Entropy Method[J].Annals of Operations Research,2005, 134(1):201-214.

[14] Kroese D P,Portsky S,Rubinstein R Y.The Cross-entropy Method for Continuous Multi-extremal Optimization[J]. Methodology and Computing in Applied Probability,2006, 8(3):383-407.

[15] 李 洁,柴天佑,宫经宽.基于交叉熵算法的PID控制器设计[J].控制与决策,2011,26(5):794-796,800.

[16] Yildiz T,Yercan F.The Cross-entropy Method for Combinatorial Optimization Problems of Seaport Logistics Terminal[J].Transport,2010,25(4):411-422.

[17] Yang X S.A New Metaheuristic Bat-inspired Algorithm [M].Berlin,Germany:Springer,2010:65-74.

[18] Yang X S.Bat Algorithm for Multi-objective Optimization [J].International Journal Bio-inspired Computation,2011, 3(5):267-274.

[19] Yang X S,Gandomi A H.Bat Algorithm:A Novel Approach for Global Engineering Optimization[J]. Engineering Computation,2012,29(5):267-289.

[20] 刘长平,叶春明,刘满成.来自大自然的寻优策略:像蝙蝠一样感知[J].计算机应用研究,2013,30(5): 1320-1322,1356.

[21] 刘长平,叶春明.具有Lévy飞行特征的蝙蝠算法[J].智能系统学报,2013,8(3):240-246.

[22] Lin J H,Chou C W,Yang C H,et al.A Chaotic Levy FlightBatAlgorithm forParameterEstimation in Nonlinear Dynamic Biological Systems[J].Computer and Information Technology,2012,2(2):56-63.

[23] 李枝勇,马 良,张惠珍.蝙蝠算法收敛性分析[J].数学的实践与认识,2013,43(12):182-190.

[24] 黄光球,赵魏娟,陆秋琴.求解大规模优化问题的可全局收敛蝙蝠算法[J].计算机应用研究,2013,30(5): 1323-1328.

[25] Nakamura R Y M,Pereira L A M,Costa K A,et al. BBA:A Binary Bat Algorithm for Feature Selection [C]//Proc.of the 25th SIBGRAPI Conference on Graphics,Patterns and Images.[S.l.]:IEEE Publication, 2012:291-297.

[26] 李枝勇,马 良,张惠珍.0-1规划问题的元胞蝙蝠算法[J].计算机应用研究,2013,30(10):2903-2906.

[27] Yao X,Liu Y,Lin G M.Evolutionary Programming Made Faster[J].IEEE Transactions on Evolutionary Computation,1999,3(2):82-102.

[28] Suganthan P N,Hansen N,Liang J J,et al.Problem Definitions and Evaluation Criteria for the CEC2005 Special Session on Real-parameter Optimisation[R]. Singapore:Nanyang Technological University,Technical Report:CEC2005005,2005.

[29] Yang Z Y,Tang K,Yao X.Large Scale Evolutionary Optimization Using Cooperative Coevolution[J]. Information Sciences,2008,178(15):2985-2999.

[30] Sun L,Yoshida S,Cheng X C,et al.A Cooperative ParticleSwarm Optimizerwith StatisticalVariable Interdependence Learning[J].Information Sciences, 2012,186(1):20-39.

编辑 索书志

图15 Zernike矩校正前后对比

从图14、图15中可以看出,空间矩和Zernike矩校正后算法检测的边缘信息明显比校正前丰富。而灰度矩校正前后效果不明显,笔者认为实际图像存在较大的噪声,而灰度矩对噪声敏感,导致校正效果不明显。

4 结束语

本文针对矩方法边缘检测存在的原理误差,采用误差校正表校正误差,通过构造理想测试图片生成误差校正表,并利用误差校正表的对称性减小校正表规模。实验结果表明,校正后比校正前检测精度提高了一个数量级。由于校正算法仅进行双线性插值,因此本文算法能够达到实时检测。本文算法仅考虑边缘距离的误差,而并未考虑误差较小的边缘角度误差,因此,针对边缘角度误差的校正算法将是下一步的研究内容。

参考文献

[1] Hueckel M H.An Operator Which Locates Edges in Digitized Pictures[J].Journal of the ACM,1971,18 (1):113-125.

[2] 尚雅层,陈 静,田军委.高斯拟合亚像素边缘检测算法[J].计算机应用,2011,31(1):179-181.

[3] Haralick R M.Digital Step Edges from Zero Crossing of Second Directional Derivatives[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1984,6 (1):58-68.

[4] Zhao Ping,Zhao Wenzhen,Duan Zhenyun,etal. Subpixel-precise Edge Extraction Algorithm Based on FacetModel[C]//Proc.ofthe 4th International Conference on Computational and Information Sciences. [S.l.]:IEEE Press,2012:86-88.

[5] Tabatabai A J,Mitchell O R,Edge Location to Subpixel Values in Digital Imagery[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1984,6(2): 188-201.

[6] Lyvers E P.Subpixel Measurements Using a Moment-based Edge Operator[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1989,11(12):1293-1309.

[7] Ghosal S,Mehrotra R.Orthogonal Moment Operators for Subpixel Edge Detection[J].Pattern Recognition,1993, 26(2):295-306.

[8] 朱遵尚,刘肖琳.基于GPU的实时亚像素Harris角点检测[J].计算机工程,2010,36(12):213-215.

[9] 刘 倩,闫宇壮,黄新生.基于边缘特征的亚像素相关匹配跟踪算法[J].计算机工程,2011,37(8):201-203.

[10] 刘亚威.空间矩亚像素图像测量算法的研究[D].重庆:重庆大学,2003.

[11] Lyvers E P,Mitchell O R.Precision Edge Contrast and Orientation Estimation[J].IEEE Transactions on Pattern Analysis and Machine Intelligence,1988,10(6):927-937.

[12] 贺忠海,廖怡白.理想边缘产生方法的研究[J].光学精密工程,2002,10(1):89-93.

编辑 顾逸斐

Cross-entropy Bat Algorithm for Solving High-dimensional Function Optimization Problem

LI Guo-cheng1,2,XIAO Qing-xian1
(1.Business School,University of Shanghai for Science and Technology,Shanghai 200093,China;
2.School of Finance and Mathematics,West Anhui University,Lu’an 237012,China)

In order to enhance the global search ability of bat algorithm in solving high-dimensional function optimization problems,a Cross-entropy Bat Algorithm(CEBA)is proposed by combining bat algorithm with CE method. The CE global stochastic optimization algorithm which is based on importance sampling and Kullback-Leibler divergence,is embedded into bat algorithm.By using adaptive smoothing technique,CEBA improves the rate of convergence.The improved algorithm fully absorbs the ergodicity,adaptability and robustness of CE,adaptively avoids the stagnancy of population,and enhances the global search ability.Simulated results conducted on classical benchmarks and 10 CEC2005 benchmarks show that the proposed algorithm possesses more powerful global search capacity,higher optimization precision and robustness.

high-dimensional function optimization;Bat Algorithm(BA);Cross-entropy(CE);importance sampling; adaptive smoothing;co-evolution

1000-3428(2014)10-0168-07

A

TP183

10.3969/j.issn.1000-3428.2014.10.032

国家自然科学基金资助项目(11171221);上海市一流学科(系统科学)基金资助项目(XTKX2012)。

李国成(1976-),男,副教授、博士研究生,主研方向:智能计算;肖庆宪,教授、博士生导师。

2013-09-25

2013-11-27E-mail:ligc313@163.com

中文引用格式:李国成,肖庆宪.求解高维函数优化问题的交叉熵蝙蝠算法[J].计算机工程,2014,40(10):168-174,180.

英文引用格式:Li Guocheng,Xiao Qingxian.Cross-entropy Bat Algorithm for Solving High-dimensional Function Optimization Problem[J].Computer Engineering,2014,40(10):168-174,180.