数据库连接池的数学建模与性能分析
2014-06-07霍占强张锦程王志衡
霍占强,张锦程,王志衡
(河南理工大学计算机科学与技术学院,河南焦作454000)
数据库连接池的数学建模与性能分析
霍占强,张锦程,王志衡
(河南理工大学计算机科学与技术学院,河南焦作454000)
为有效地配置数据库连接池中的系统参数,根据数据库连接池管理过程的工作原理,引入离散时间排队论的思想,建立多服务台损失制的Geom/Geom/c/c离散时间排队模型。采用嵌入马尔科夫链方法,分析系统稳态队长的转移概率矩阵及其满足的递推关系式。应用模型的理论分析结果,导出请求阻塞概率、系统平均连接数、系统利用率、系统吞吐量等系统性能指标的数学表达式。通过实验证明了数据库连接池性能指标与系统配置参数之间的依赖关系。
数据库连接池;性能分析;数学建模;离散时间排队论;Geom/Geom/c/c模型;多服务台
1 概述
在软件系统开发过程中,数据库访问是非常重要的环节,特别是在信息管理系统的开发过程中,数据库访问是必不可少的步骤。数据库连接作为一种与数据库交互的关键资源,在应用程序尤其是多用户的网页程序中显得尤为重要。连接的复用能够提高连接的利用率,提高系统对数据库操作的性能,减少系统开销。连接池的核心是连接复用,因此数据库连接池在系统开发中的应用越来越广泛。
文献[1]通过3种不同的数据库访问模式下的性能对比测试,对基于连接池的数据库访问性能的提高给出了一个定量的数据。文献[2]提出基于日志文件记录的数据库连接池的自优化配置方法。文献[3]给出了在J2EE架构下,基于XML的数据库连接池参数配置的详细配置方法。文献[4-6]从数据库连接池技术的具体实现和性能优化的角度进行了研究并取得一些有意义的成果。以上文献要么应用实测数据分析的方法进行研究,要么从数据库连接池实现及优化的角度进行研究,目前尚未发现应用数学模型的方法对数据库连接池技术进行性能分析的文献。
数据库连接池技术性能分析及评价的研究方法可分为3类[7]:实测数据分析方法,仿真研究方法以及数学模型分析方法。其中,数学模型分析方法具有既适用于已有的系统,又适用于尚未存在的系统且分析费用低的特点[8-9]。本文应用数学模型分析方法,为数据库连接池技术建立了离散时间多服务台排队模型。经典离散时间排队模型的分析可见文献[10,11-13]等。
本文根据数据库连接池技术的工作原理,建立多服务台损失制的Geom/Geom/c/c离散时间排队模型,对模型进行了理论分析,并导出请求阻塞概率、系统平均连接数、系统利用率、系统吞吐量等系统性能指标的表达式。
2 数据库连接池的管理过程
连接池的管理是数据库连接池工作原理中的重要组成部分。在数据库连接池中,连接可以分为正在使用的连接(忙碌连接)和未被使用的连接(空闲连接)2种。连接池管理过程如图1所示。

图1 数据库连接池管理过程
连接池管理过程具体如下:
(1)当客户请求数据库连接时,首先查看连接池中是否有空闲连接,如果存在空闲连接,则取出一个空闲连接分配给客户使用,同时将该连接标记为忙碌连接,如图1中①所示。
(2)如果没有空闲连接,则查看当前空闲连接和忙碌连接的总数是否已经达到系统设置的最大连接数,如果没达到就重新创建一个连接给请求的客户,如图1中②所示;如果达到就按设定的最大等待时间进行等待,如果超出最大等待时间,则抛出异常给客户,如图1中③所示。
(3)当客户使用连接结束时,将连接放回连接池中,以提高连接复用率,同时将该连接标记为空闲连接,如图1中④所示。
在数据库连接池的管理过程中,将一个数据库连接看作一个服务台,将一个连接请求看作一个顾客的到达。假设客户请求的到达过程为Bernolli到达过程,一个连接的使用时间服从几何分布,最小连接数等于最大连接数且在没有空闲连接的情况下,连接请求被拒绝,采用先到先服务的策略,可将数据库连接池的管理过程建模为多服务台损失制的Geom/Geom/c/c离散时间排队模型。
3 排队模型的描述和分析
3.1 模型描述
时间轴被分割为固定间隔的小段,称为时隙。到达只能发生在每个时隙的末端t=n-处(n=1, 2,…),称为晚到系统。
为明确定义离散时刻t=n时系统中的顾客数,约定服务开始和结束都发生于t=n处。如果顾客于n-到达,并且在t=n时有顾客离开,则在t=n时可立即开始服务。这样的系统称为有直接入口[12]。顾客到达和离去行为如图2所示。
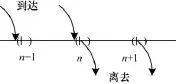
图2 顾客到达与离去行为示意图
每一个时隙末端以概率p发生一个到达,以概率p—=1-p无到达,不同时隙上的到达相互独立。换言之,到达间隔T服从几何分布:

顾客的服务时间S也服从几何分布:

到达间隔与服务时间相互独立。系统中有c个服务台,如果顾客到达遇c个服务台都被占用,并且没有顾客在他到达的时刻离开,该顾客将被拒绝进入系统。
3.2 模型分析
设Ln=L(n+)表示时刻t=n+在系统中的顾客数。按到达和离去行为的约定,t=n-到达的顾客将计入Ln,而时刻t=n离去的顾客不计入在内。{Ln,n≥1}是一个Markov链,有状态空间Ω={0,1,…,c},转移概率矩阵具体如下:

其中:

并且:


设 Markov链的极限分布为 Π,以 Π={π0,π1,…,πc}表示{Ln,n≥0}的极限分布,引入:

由文献[12]中的定理可知,稳态对长概率π0,π1,…,πc满足递推关系平稳分布和正规化条件,可以得到以下关系式:

其中,k=0,1,…,c-2。
3.3 稳态概率分布的求解算法
由式(3)、式(4)可知,π0,π1,…,πc之间具有线性关系,假设πc=1,由πc可以求得πc-1,再由πc和πc-1可以求得πc-2,依次类推,可以一直求得π0。应用正规化条件π0+π1+…+πc=1可得出模型的稳态概率分布π0,π1,…,πc。具体求解算法的流程如图3所示。

图3 稳态概率分布求解算法流程
4 数据库连接池的性能指标分析
数据库连接池的性能指标分析具体如下:
(1)请求阻塞概率,即一个数据库连接请求因系统中没有可用连接而被拒绝的概率,记为pl。请求阻塞概率是衡量一个数据库连接池系统服务质量的重要指标。若请求阻塞概率过高,则应为系统配置更高的最大连接数。为此,可能需要使用性能更好的数据库管理系统。请求阻塞概率的数学表达式为:pl=πcc。
(2)系统平均连接数,即在稳态下数据库连接池建立连接数的均值,记为。系统平均连接数反映了系统运行稳定后系统的实际并发用户数,它为数据库连接池技术配置参数提供了重要理论依据,其数学表达式为:。
(3)系统利用率,即连接用户数与连接池可建立的最大连接数c的比,记为η。系统利用率的高低直接关系系统资源的使用情况,分析系统利用率的影响因素,对数据库连接池技术的参数配置有着重要参考意义,其数学表达式为:。

5 实验与结果分析
为直观地展示数据库连接池性能指标与系统配置参数之间的依赖关系,下文给出了在不同条件下,请求阻塞概率、系统平均连接数、系统利用率及系统吞吐量随请求到达率、最大连接数变化的趋势。将相关参数设置为:每个时隙连接请求到达的概率p设为0.1~0.9,每个时隙连接服务完成的概率μ设为0.03,最大连接数c设为1~32。
图4是当服务率设为0.03,最大连接数分别设为4,8,16和32时,请求阻塞概率随到达率的变化曲线。当服务率μ和最大连接数c一定的条件下,请求阻塞概率随请求到达率p的增大而增大。这是因为伴随连接请求的增多,服务台能够及时处理的连接请求就减少,相应未能处理的连接数就增大,进而请求阻塞概率增大;当连接完成的服务率μ和请求到达率p一定的条件下,请求阻塞概率随着最大连接数c的增大而减小。这是因为当最大连接数增大时,单位时间内能够完成的连接数就增多,相应的未能处理的连接数就减少,即请求阻塞概率就减小。

图4 请求阻塞概率随到达率的变化
图5是当服务率设为0.03,请求到达率分别设为0.2,0.4,0.6和0.8时,请求阻塞概率随最大连接数的变化曲线。当服务率μ和请求到达率p一定的条件下,请求阻塞概率随最大连接数c的增大而减小;当服务率μ和最大连接数c一定的条件下,请求阻塞概率随请求到达率p的增大而增大。

图5 请求阻塞概率随最大连接数的变化
图6是当服务率设为0.03,最大连接数分别设为4,8,16和32时,系统平均连接数随到达率的变化曲线。

图6 系统平均连接数随到达率的变化
当服务率μ和最大连接数c一定的条件下,系统平均连接数随请求到达率p的增大而增大并趋近于定值c。这是因为伴随连接请求的增多,单位时间内建立服务的连接就增多,相应的系统平均连接数就增多,当超过系统负载后,系统平均连接数固定为c;当服务率μ和请求到达率p一定的条件下,系统平均连接数随最大连接数c的增大而增多。这是因为伴随最大连接数的增大,能够建立服务的连接数就增多,相应的系统平均连接数就增多。
图7是当服务率设为0.03,顾客到达率分别设为0.2,0.4,0.6和0.8时,系统平均连接数随最大连接数的变化曲线。当服务率μ和请求到达率p一定的条件下,系统平均连接数随最大连接数c的增大而增大;当服务率μ和最大连接数c一定的条件下,系统平均连接数随请求到达率p的增大而增多。

图7 系统平均连接数随最大连接数的变化
图8是当请求到达率设为0.03,最大连接数分别设为4,8,16和32时,系统利用率随到达率的变化曲线。当服务率μ和最大连接数c一定的条件下,系统利用率随请求到达率p的增大而增大并趋近于1。这是因为伴随连接请求的增多,单位时间内建立服务的连接就增多,相应的系统利用率就增大,直到系统满负载运行;当服务率μ和请求到达率p一定的条件下,系统利用率随最大连接数c的增大而降低。这是因为伴随最大连接数的增大,单位时间内能够完成的连接数增多,相应空闲连接就增多,即系统利用率降低。

图8 系统利用率随到达率的变化
图9是当服务率设为0.03,请求到达率分别设为0.2,0.4,0.6和0.8时,系统利用率随最大连接数的变化曲线。当服务率μ和请求到达率p一定的条件下,系统利用率随最大连接数c的增大而降低;当服务率μ和最大连接数c一定的条件下,系统利用率随请求到达率p的增大而增大。

图9 系统利用率随最大连接数的变化
图10是当请求到达率设为0.03,最大连接数分别设为4,8,16和32时,系统吞吐量随到达率的变化曲线。当服务率μ和最大连接数c一定的条件下,系统吞吐量随请求到达率p的增大而增大,并趋近于定值。这是因为伴随连接请求的增多,单位时间内建立服务的连接就增多,相应的系统吞吐量就增大,直到系统满负载运行;当服务率μ和请求到达率p一定的条件下,系统吞吐量随最大连接数c的增大而增大。这是因为伴随最大连接数的增大,能够建立服务的连接数就增多,相应的系统吞吐量就增大。

图10 系统吞吐量随到达率的变化
图11是当服务率设为0.03,请求到达率分别设为0.2,0.4,0.6和0.8时,系统吞吐量随最大连接数的变化曲线。当服务率μ和请求到达率p一定的条件下,系统吞吐量数随最大连接数c的增大而增大;当服务率μ和最大连接数c一定的条件下,系统吞吐量随请求到达率的增大而增大。

图11 系统吞吐量随最大连接数的变化
6 结束语
本文分析了数据库连接池的工作原理,根据其工作原理建立了多服务台损失制的Geom/Geom/c/ c离散时间排队模型,完成了模型的理论分析,并导出了请求阻塞概率、系统平均连接数、系统利用率及系统吞吐量等系统性能指标的表达式,通过实验讨论了请求到达率和最大连接数对系统性能的影响,该研究成果为数据库连接池技术的参数配置提供了理论依据。下一步工作是为模型增加排队场所等条件约束,对数据库连接池进行更精确的性能分析与评价。
[1] 王宇杰,王 锋,杨文宾.基于数据库连接池的数据库访问性能对比测试研究[J].工业控制计算机, 2010,23(6):92-94.
[2] 李秉璋,吴访升,景征骏,等.NVMS中的自适应数据库连接池技术[J].计算机工程,2008,34(23):41-43.
[3] 朱长生,沈云付.自适应数据库连接池的研究[J].计算机工程与应用,2003,39(36):187-189.
[4] 梁清翰,沈占锋,骆剑承,等.构建LBS系统的数据库连接池技术研究[J].计算机工程,2006,32(12): 39-41.
[5] 孟培超,胡圣波,舒 恒,等.基于ADO数据库连接池优化策略[J].计算机工程与设计,2013,34(5): 1706-1710.
[6] 曾国林,傅秀芬.一种新的数据库连接池模型的研究[J].计算机与数字工程,2011,39(2):163-166.
[7] 吕健波,戴冠中,慕德俊.绝对延迟保证在Web应用服务器数据库连接池中的实现[J].计算机应用研究, 2012,29(5):1838-1841.
[8] Lu Jianbo,Dai Guanzhong,Mu Dejun.Solutions for Supporting Qos in Database in Web Application servers [J].International Journal of Digital Content Technology and Its Applications,2012,6(11):213-222.
[9] Liu Fei.A Method of Design and Optimization of Database Connection Pool[C]//Proc.ofthe 4th International Conference on Intelligent Human-Machine Systems and Cybernetics.Washington D.C.,USA:IEEE Computer Society,2012:272-274.
[10] Takagi H.Queuing Analysis,Vol.3:Discrete-time systems[M].Amsterdam,Holland:[s.n.],1993.
[11] Tian Naishuo,Zhang Z G.Vacation Queuing Models: Theory and Applications[M].[S.l.]:Springer-Verlag,2011.
[12] 田乃硕,徐秀丽,马占友.离散时间排队论[M].北京:科学出版社,2008.
[13] 田乃硕,刘洺辛,马占友,等.Erlang消失系统的离散时间建模分析[J].系统工程与电子技术,2006,26 (6):823-828.
编辑 陆燕菲
Mathematical Modeling and Performance Analysis of Database Connection Pool
HUO Zhan-qiang,ZHANG Jin-cheng,WANG Zhi-heng
(School of Computer Science and Technology,Henan Polytechnic University,Jiaozuo 454000,China)
In order to configure the system parameters of database connection pool effectively,a Geom/Geom/c/c discrete-time queuing model with multi-server is built according to the operation mechanism of its manage process and the thought of discrete-time queuing theory.It uses the embedded Markov chain method,and the matrix of transition probability and matching recursive relations of the stationary queue length are given.The mathematical expressions of system performance measures are derived by the theoretical analysis results of the model,such as request blocking probability,average number of connections,system utilization,and system throughput,etc.Experiments are intuitively given to prove the dependencies between database connection pool performance index and system configuration parameters.
database connection pool;performance analysis;mathematical modeling;discrete-time queueing theory; Geom/Geom/c/c model;multi-server
1000-3428(2014)10-0032-05
A
TP302
10.3969/j.issn.1000-3428.2014.10.007
国家科技部创新方法工作专项基金资助项目(2011IM010300)。
霍占强(1979-),男,副教授、博士,主研方向:网络性能分析,数据库技术;张锦程,硕士研究生;王志衡(通讯作者),副教授、博士。
2013-11-08
2013-12-06E-mail:wzhenry@eyou.com
中文引用格式:霍占强,张锦程,王志衡.数据库连接池的数学建模与性能分析[J].计算机工程,2014,40(10):32-36.
英文引用格式:Huo Zhanqiang,Zhang Jincheng,Wang Zhiheng.Mathematical Modeling and Performance Analysis of Database Connection Pool[J].Computer Engineering,2014,40(10):32-36.
