交流连续调谐滤波器失谐度的无盲区检测方法

邓亚平， 同向前， 鲍 洋， 冯 颖

（西安理工大学自动化与信息工程学院，陕西西安 710048）

交流连续调谐滤波器失谐度的无盲区检测方法

邓亚平， 同向前， 鲍 洋， 冯 颖

（西安理工大学自动化与信息工程学院，陕西西安 710048）

失谐度的在线测量是交流连续调谐电力滤波器中的关键环节之一，其检测精度会影响到滤波器的性能及其运行的稳定性。针对目前调谐滤波器失谐度间接测量方法所存在的检测盲区问题，提出了一种基于滤波电容器和电抗器两端谐波电压幅值的失谐度测量方法，该方法克服了失谐度检测盲区的问题，且实现简单方便；建立了交流连续调谐滤波器的失谐度检测实验系统，实验结果表明该失谐度检测方法是有效准确的。

计量学；调谐滤波器；失谐度；谐波电压

1 引 言

尽管有源滤波器具有优良的性能，然而在高压系统中，调谐滤波器仍然处于无可替代的地位。为了解决调谐滤波器固有的失谐问题［1，2］，目前国内外广泛开展了交流自动连续调谐滤波器的研究［3～10］。失谐度的检测是实现自动连续调谐滤波器的基础，也是影响自动连续调谐滤波器的滤波性能及其运行稳定性的重要因素［9］。

失谐度的直接在线检测非常困难，因此，通常从失谐的原因和后果来探讨失谐度的间接测量方法。文献［11］提出了一种基于滤波支路谐波无功功率的失谐度间接测量方法，利用滤波支路谐波无功功率的正负和大小反映滤波器的失谐程度。然而，滤波支路谐波无功功率的大小与滤波器母线谐波电压、滤波支路谐波电流及电网谐波阻抗均有关系，且其数值与失谐度之间也不存在确定的对应关系，应用起来较为困难。文献［12］提出了一种基于滤波器谐波相位的失谐度间接测量方法，滤波器的谐波相位易于测量［13］，可以反映滤波器的失谐程度，且其数值变化范围是确定的，与失谐度之间也存在确定的直接对应关系。

无论是基于谐波功率还是基于谐波相位的失谐度检测方法，均要检测滤波器的母线谐波电压，但是，在滤波器完全调谐时，母线谐波电压趋于零，导致出现检测盲区或精度低的问题。本文提出了一种基于滤波元件谐波电压的滤波器失谐度检测新方法，既可满足滤波器失谐度的测量值与理论失谐度之间存在确定对应关系的要求，又可有效避免滤波器完全谐振时出现的检测盲区。

2 失谐度的无盲区检测新方法

图1给出了无源单调谐滤波器的结构示意图，它是由滤波电感、滤波电容和等值电阻串联而成，兼备特定h次谐波抑制和无功功率补偿的双重作用，图2给出了无源滤波系统相对应的h次谐波等值电路。

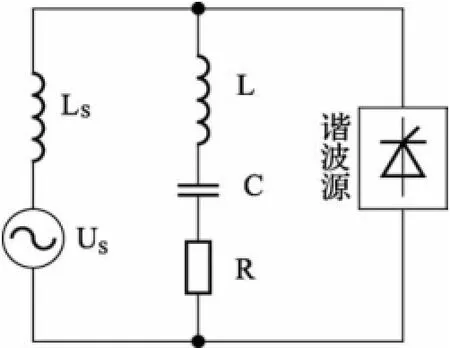
图1 无源单调谐滤波器结构图

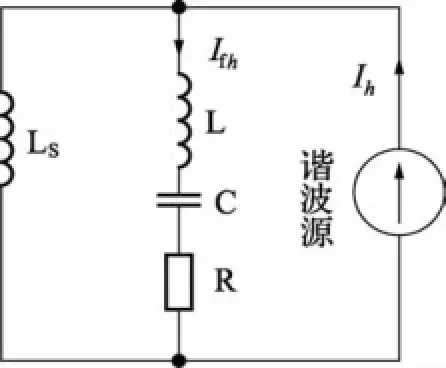
图2h次谐波等值电路

设滤波器中滤波电感与电容分别为L、C，滤波器的实际谐振角频率为ωr，则存在以下关系

设电网h次谐波角频率为ωh，按照失谐度的定义［14］，滤波器对h次谐波的理论失谐度δ0为

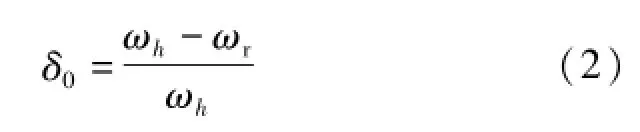
若滤波电抗器与电容器两端的h次谐波电压幅值分别表示为ULh、UCh，则本文所提出的基于ULh、UCh的失谐度测量值δ可表示为

显然，当调谐滤波器完全谐振于h次谐波时，失谐度测量值δ等于零；当调谐滤波器发生失谐时，随着失谐的严重，δ也逐渐趋近于＋1或－1。因此，δ的大小反映了失谐的程度，正负反映了失谐的方向。

假设流过滤波支路的h次谐波电流为Ifh，滤波器中滤波电抗器与电容器的h次谐波阻抗分别表示为XLh、XCh，则由图2可得在忽略滤波电抗器等值电阻时，δ的表达式为

将式（1）、式（2）代入式（4），可得此时失谐度测量值δ与理论失谐度δ0之间的关系为

考虑到在失谐度的通常变化范围内，即－0.2≤δ0≤0.2时，下式成立

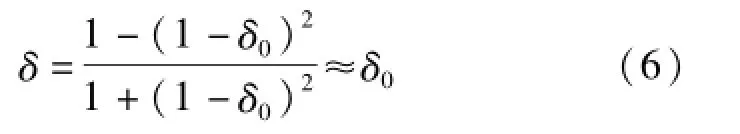
上式表明，通过检测滤波电感和滤波电容两端电压的h次谐波电压幅值，可以间接得到失谐度。

图3给出了理论失谐度δ0在区间［－0.2，0.2］变化时，失谐度测量值δ与理论值δ0的关系曲线。由图可知，失谐度测量值δ与理论值δ0之间是一一对应的线性关系，真实准确地反映了失谐度的性质和大小。

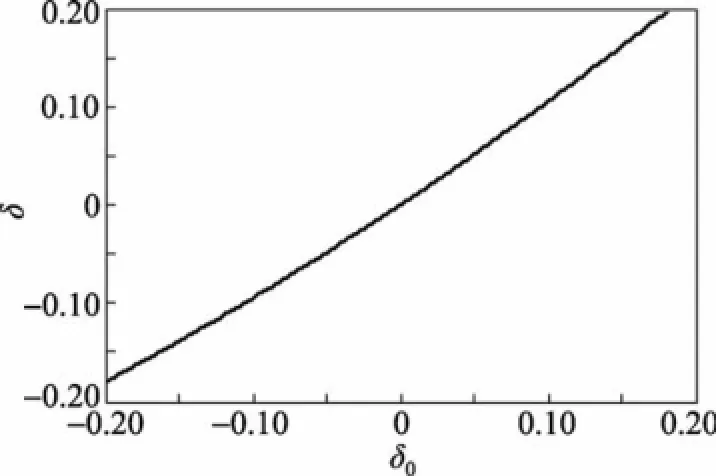
图3 理论失谐度δ0与实测失谐度δ的关系曲线

3 电抗器等值电阻对测量结果的影响

在实际工程应用中，滤波电抗器中通常均含有一定的等值电阻，从滤波电抗器两端测取的谐波电压包含滤波电感电压和等值电阻上的电压，从而可能影响到测量结果的精度。

设电网基波角频率为ω1，根据滤波电抗器品质因数q的定义［15］，滤波电抗器等值电阻R可表示为

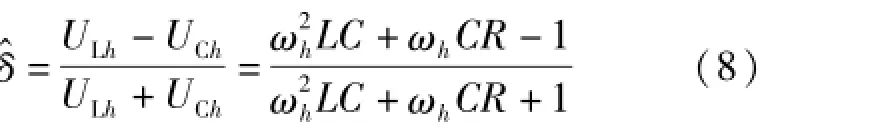
将式（1）、式（2）、式（7）代入式（8），可得此时失谐度测量值与理论失谐度δ0之间的关系

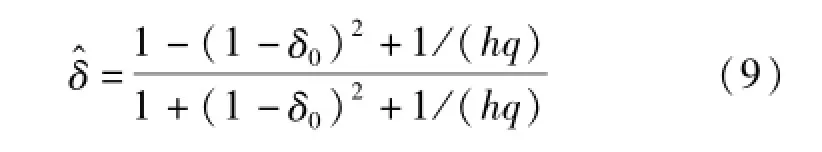
式中，h为谐波次数。考虑到δ0的较小变化范围，上式可简化为

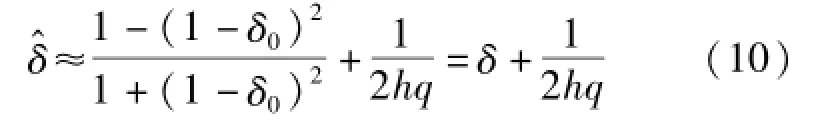
上式表明滤波电感等值电阻对δ＾的影响较小，其对失谐度检测结果的影响可以忽略不计。如h＝5，q＝20，由于忽略电抗器等值电阻而引入的失谐度检测误差绝对值仅为0.005。

图4给出了h＝5，滤波电抗器品质因数q分别为20、60和∞的3种情况下，理论失谐度δ0在区间［－0.2，0.2］变化时，由式（9）计算所得的失谐度测量值δ＾与理论值δ0的关系曲线。由图可见，3条曲线基本重合，即电抗器品质因数对失谐度检测的影响可以忽略不计。

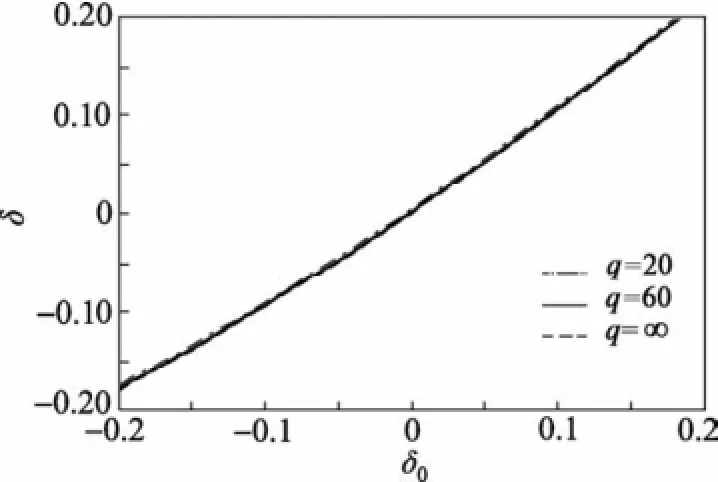
图4 不同q值时δ0与的关系曲线

4 误差分析与修正

4.1 误差分析

失谐度的相对测量误差ε可反映测量值δ偏离理论值δ0的程度，其定义式为

将式（5）代入式（11），可得

在失谐度的通常变化范围内，即－0.2≤δ0≤0.2时，下式成立

4.2 算法修正

由式（13）可得

结合式（3），可得失谐度检测算法的修正式

图5给出了失谐度真值δ0在区间［－0.2，0.2］变化时，由式（3）得到的测量值δ和由校正式（15）得到的测量值δ′相对于δ0的误差百分数。可以看出，式（3）的检测误差ε不超过10%，而修正式（15）的检测误差ε′不超过2%。

图5 理论失谐度δ0与误差ε、ε′的关系曲线

如果考虑到滤波电抗器等值电阻引入的误差，失谐度检测公式可以进一步修正为

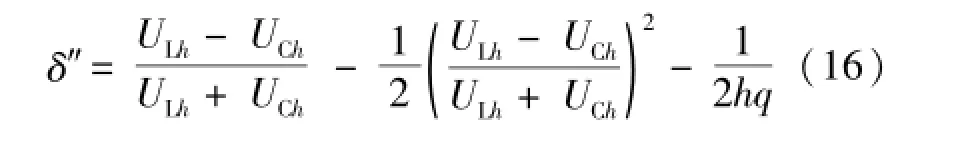
5 两种失谐度检测方法的比较

图6给出了q＝20时，文献［12］所提出的失谐度检测方法中失谐度测量值与谐波相位之间的关系曲线。

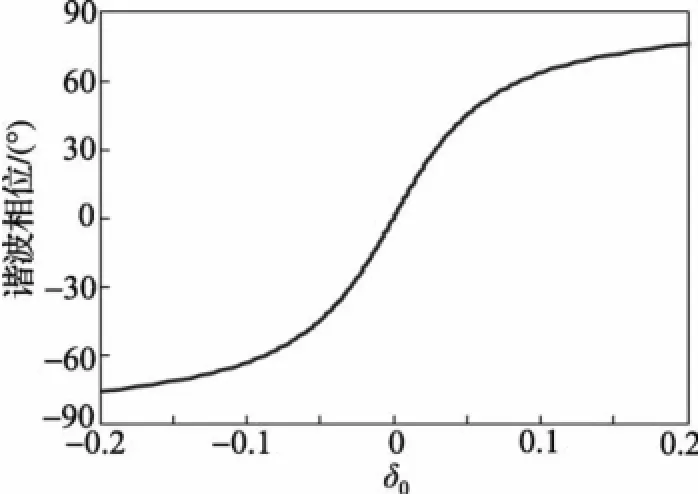
图6 失谐度与谐波相位的关系曲线

对比图3与图6可知，本文提出的失谐度检测新方法在更大的失谐度范围内均具有良好的线性关系。

特别值得指出，随着滤波器对某次谐波的精确调谐控制，滤波器母线电压中的该次谐波分量逐渐趋于零，原有基于谐波相位的失谐度检测方法将存在无法检测的盲区问题。本文提出的失谐度检测方法是通过检测滤波电抗器和滤波电容器上的谐波电压幅值来进行失谐度检测的，在滤波器完全谐振时，虽然滤波器母线电压的h次谐波分量达到最小，但是，滤波器中的h次谐波电流分量却达到最大，即滤波电抗器和滤波电容器上的谐波电压此时最大，因此该方法不存在检测盲区问题。

6 仿真与实验结果

6.1 仿真结果

为了验证上述理论分析的正确性，本文在PSIM和MATLAB联合仿真环境下，搭建了LC无源滤波器的失谐度在线检测仿真系统。其中，系统电源电压为10 kV，频率为50 Hz。LC滤波器中的电容器为75μF，电抗器的品质因数为50，电感值通过开关投切以实现滤波器失谐度的改变。仿真系统中，首先采用离散傅里叶变换分别检测得到滤波电容器和滤波电抗器上的5次谐波电压幅值，然后采用式（15）所示的失谐度检测方法分析计算滤波器的5次谐波失谐度。

表1中谐振频率ωr根据式（1）计算得到，理论失谐度δ0根据式（2）计算得到，实测失谐度δ由仿真系统按式（15）计算得到。

表1 仿真测试结果

表1的测试数据表明，在失谐度为－0.2～0.2的正常变化范围内，基于LC元件谐波电压幅值的失谐度测量结果是准确的。

6.2 实验结果

6.2.1 对比实验

为了验证本文所提出的失谐度检测方法在实际工程应用时的可行性及相对于文献［12］中所提出原有检测谐波相位方法的优越性，本文搭建了滤波器的失谐度在线检测实验系统。为了能够对滤波器的实际失谐度进行实时调节，实验系统采用的是滤波电抗器的电感值可以进行不断连续调节的有源电抗器和一组固定电容器共同构成的滤波器来进行实验。

图7给出了一种基于电感值可连续调节的有源电抗器的滤波器［9］采用本文所提出失谐度检测方法时的实验系统框图。其中，LC构成一组无源调谐滤波器，APF并联于滤波电抗器L两端，且是由4个IGBT器件构成的单相电压源变换器。前期的研究结果已经表明［9］，通过合理调整APF输出的h次谐波补偿电流iCh的大小和方向，可以达到对滤波电抗器L的h次谐波等效电感值进行连续调节，进而可以实现对LC滤波器的h次谐波失谐度进行实时调节的功能。首先，调整APF输出的h次谐波补偿电流iCh达到对滤波电感值的连续调节；其次，采用本文所提出的检测方法和文献［12］中提出的失谐度检测方法，分别由式（15）和原有检测方法所采用的相位差计算得到滤波器的实际失谐度δ和δ′。实验系统中，选择电抗器的初始电感值L为15.4 mH，电容值C取为75μF。以5次谐波为例，两种失谐度检测方法的实验测试结果见表2。

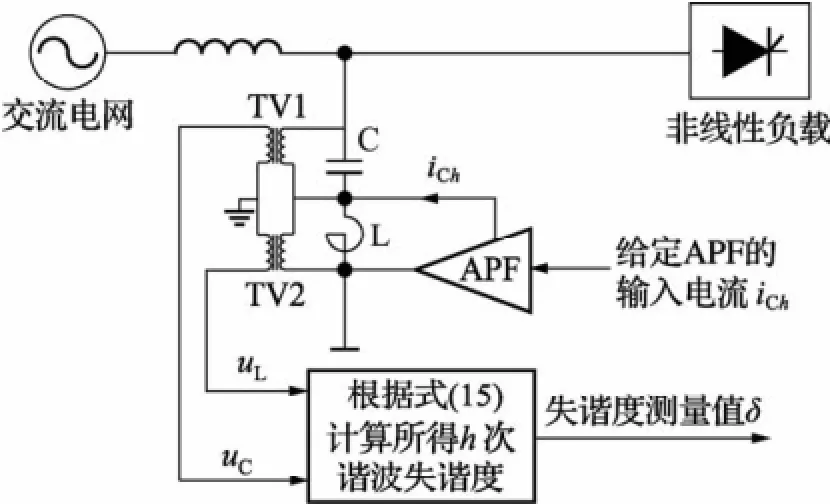
图7 失谐度检测方法的实验系统框图

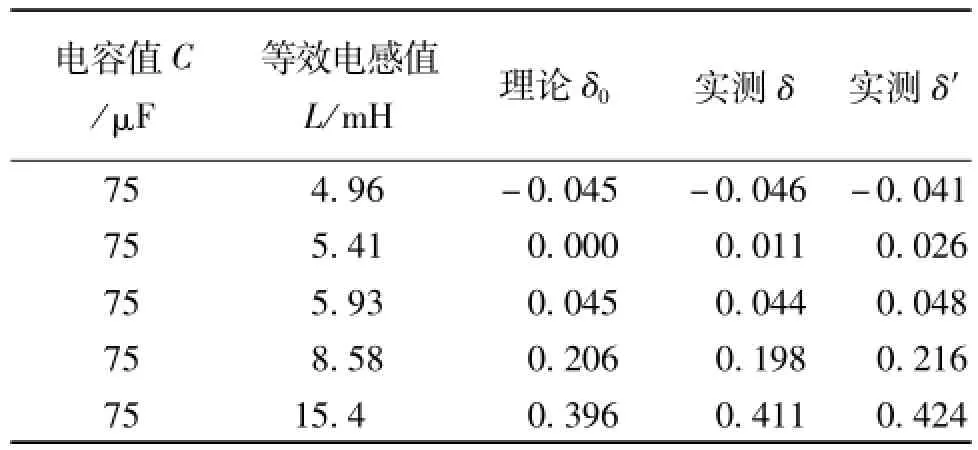
表2 实验测试结果

对比表2中的测试结果可知，在滤波器的失谐度较大时，本文所提出的方法与原有失谐度检测方法均具有较高的检测精度，而在滤波器完全调谐，也即滤波器的失谐度接近于0时，原有方法的检测精度差，而本文所提出失谐度的检测方法仍然具有较高的检测精度，有效避免了文献［12］中失谐度检测方法在完全调谐时所存在的检测盲区问题。

6.2.2 应用实例

图8给出了一种基于本文所提出失谐度检测方法进行谐波抑制时的有源调谐型混合滤波器的系统框图，通过控制APF输出的谐波电流可以实现混合滤波器对多次谐波的连续调谐。首先检测LC两端的谐波电压，由式（15）计算得到滤波器的实际失谐度δ，再通过调谐控制器调整APF输出的h次谐波补偿电流iCh，达到对h次谐波连续调谐的目的。实验系统中，选择L的值为15.4 mH和C为75μF，偏调谐于3次谐波，而APF工作时对5、7次谐波同时进行调谐控制。

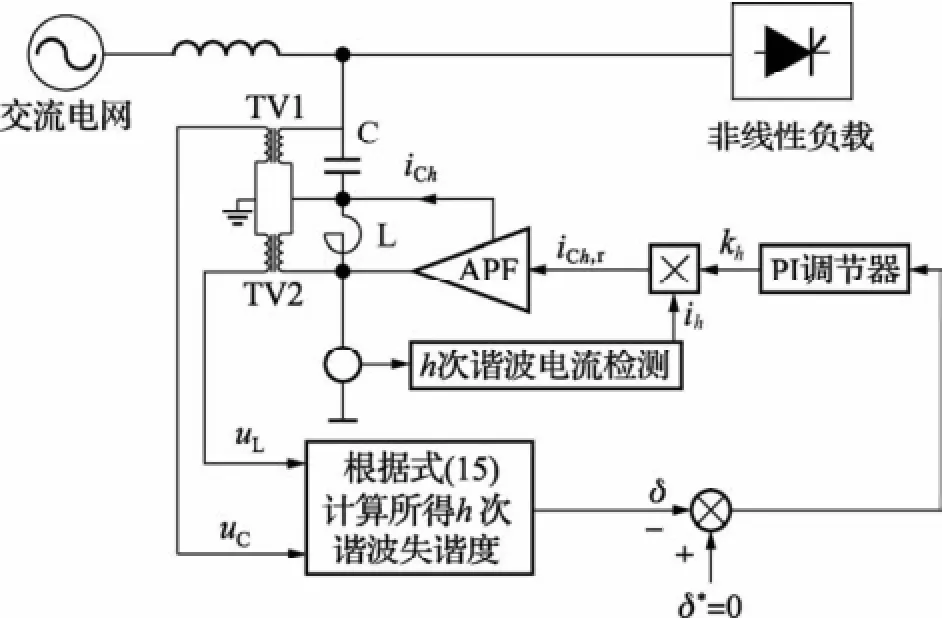
图8 失谐度检测方法的应用实施例

表3列出了LC无源滤波器的理论失谐度和APF工作前后混合滤波器的实测失谐度。当APF不调谐时，混合滤波器等同于无源滤波器；当APF工作后，混合滤波器自动连续地同时调谐于5次和7次谐波，混合滤波器的5次和7次谐波的失谐度显著下降。

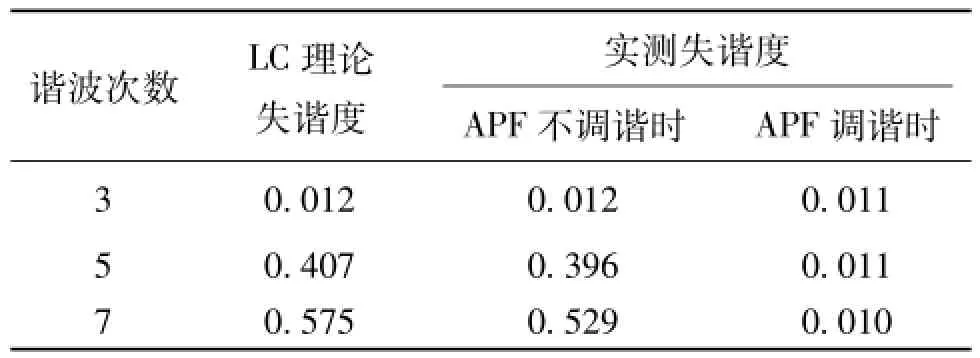
表3 实验测试结果

7 结 论

（1）利用滤波电抗器与电容器两端谐波电压幅值可以有效准确地测量调谐滤波器的失谐度。

（2）滤波电抗器等值电阻对失谐度检测精度的影响较小，可以忽略不计。

（3）在调谐滤波器的正常失谐范围内，本文所提失谐度检测方法的测量误差不超过2%。

［1］ Das JC.Passive filters-potentialities and lim itations［J］.IEEE Transactions on Industry Applications，2004，40（1）：232－241.

［2］ Shuai Z，Luo A，Tu C，et al.New control method of injection-type hybrid active power filter［J］.IET Power Electronics，2011，4（9）：1051－1057.

［3］ Bula D，Pasko M.Hybrid power filter with single tuned passive filter-dynamical properties［C］／／2010 International School on Nonsinusoidal Currents and Compensation，Lagow，Poland，2010.

［4］ Nelson David Epp.A self-tuning filter for them itigation of power system harmonics［D］.Edmonton：University of Alberta，2000.

［5］ Tian J，Chen Q，Xie B.Series hybrid active power filter based on controllable harmonic impedance［J］.IET Power Electronics，2012，5（1）：142－148.

［6］ Corasaniti V F，Barbieri M B，Arnera P L，et al.Hybrid power filter to enhance power quality in amedium-voltage distribution network［J］.IEEE Transactions on Industry Electronics，2009，56（8）：2885－2893.

［7］ Verma V，Singh B.Design and implementation of a currentcontrolled parallel hybrid power filter［J］.IEEE Transactions on Industry Applications，2009，45（5）：1910－1917.

［8］ 康明才，于明涛，陈建业，等.基于裂芯式可控电抗器双调谐滤波器研究［J］.电力系统自动化，2005，29（15）：53－57.

［9］ 同向前，伍文俊，任碧莹.电压源换流器在电力系统中的应用［M］.北京：机械工业出版，2012.

［10］ 武健，何娜，徐殿国.并联混合有源滤波器复合控制策略［J］.电力自动化设备，2009，29（3）：97－100.

［11］ Bradley D A.Tutorial guides in electronics engineerings：Power Electronics［M］.London：Chapman Hall Press，1996.

［12］ 同向前，周世平，薛钧义.交流调谐滤波器失谐度检测方法的研究［J］.仪器仪表学报，2005，26（5）：658－660.

［13］ 张家生，刘扬.相位检测方法研究［J］.仪器仪表学报，2005，26（5）：658－660.

［14］ 程浩忠，艾芊，张志刚，等.电能质量［M］.北京：清华大学出版社，2006.

［15］ 邱关源.电路（第5版）［M］.北京：高等教育出版社，2006.

A No-blind Area Detection Method of Detuning in Continuously Tuned AC Filter

DENG Ya-ping， TONG Xiang-qian， BAO Yang， FENG Ying
（School of Automation and Information Engineering，Xi'an University of Technology，Xi'an，Shannxi710048，China）

The measurement of detuning is a very crucial step in continuously tuned AC filter，and the detection precision can affect the filtering performance and operation stability.To solve the problem of detection dead zone in existing indirectlymeasurement of AC filter detuning，a new detection method based on the harmonic voltage crossed between the filter reactor and capacitor is proposed.The presented method not only overcomes the detection blind area，but also has advantages of simp le implementation.A detuning detection experimental system is developed，and the results show the effectiveness and accuracy of the proposedmethod for filter detuning.

Metrology；Tuned filter；Detuning；Harmonic voltage

TB971

A

1000-1158（2014）04-0368-05

10．3969／j．issn．1000-1158．2014．04．14

2013-10-18；

2014-03-11

陕西省重点学科建设专项资金和高等学校博士学科点专项科研基金（2012611810009）

邓亚平（1984－），女，山西运城人，西安理工大学博士。研究方向为混合电力滤波器的研究与应用。xautdodo＠163.com