基于光束法平差单点三坐标测量的新方法

冉险生， 朱才朝， 林 立

（1.重庆大学机械传动国家重点实验室，重庆 400030； 2.重庆交通大学机电与汽车工程学院，重庆 400074）

基于光束法平差单点三坐标测量的新方法

冉险生1，2， 朱才朝1， 林 立2

（1.重庆大学机械传动国家重点实验室，重庆 400030； 2.重庆交通大学机电与汽车工程学院，重庆 400074）

在研究多组像片内方位元素的修正和全局光束法平差的基础上，提出使用3台像机同时对测棒进行数据采集，通过光束法平差实现单点三坐标测量的新方法，并完成系统硬件的组建。通过实验，将新系统测量的结果与计量型三坐标仪测量值进行比较，得到系统的相对测量精度高于1∶29061，优于单、双像机系统，能够满足工业产品的检测需求。

计量学；光束法平差；单点测量；三像机系统；测棒

1 引 言

传统的单点近景摄影测量系统有单像机和双像机成像。单像机成像是利用单台像机获取单张像片进行空间点三维坐标测量，实质是借助一根空间点已知的测棒，构建辅助测量坐标系（测棒坐标系），实现测棒坐标系、测量坐标系、像坐标系之间的相互转换，利用单像空间后方交会原理解算出像片外方位元素，求得空间点坐标［1］，其精度通常为1∶2 000。虽然单像机系统结构简单、成本较低，但测量质量、精度均不理想，因而实际工作中引入利用空间前方交会的双像机成像系统，成像像机增加为2台。根据交会摄影测量原理，为实现物方点的精确定位，需要已知像机内、外方位元素才能求解。对于内方位元素可以通过像机的标定来得到，而像机的外方位元素往往不易求得。虽然在像机内方位元素已知的条件下，可以仅根据两幅图像之间的对极几何约束来测量目标表面若干特征点的空间三维位置［2］，但这需要一个先决条件是：两像机光心的距离已知。对于像机位置并不固定的近景摄影系统，此方法并不适用。因而实际双像机测量系统仍然是单像后方交会测量系统的推广。首先两台摄像机分别使用单像后方交会原理求解内外方位元素，使之满足线-线交会的基本条件，然后通过线-线交会原理求解空间坐标点。与单像机系统相比，双像机系统的测量稳定性、鲁棒性有了大幅度提高，其相对测量精度可达1∶20 000［3］。相对于测量精度可达1∶500 000的工业近景摄影系统，上述双像机单点三坐标测量（CMM）系统测量精度仍然偏低，限制了设备在高精度产品空间尺寸测量上的应用。

针对以上问题，本文提出一种基于光束法平差原理，使用3台像机完成单点三坐标测量的新方法。其在对获取像片的处理上，引入光束法平差算法来提高测量的精准度。通过3个处于不同位置的数码像机同时对测棒进行交会拍照，，实现未知点空间三维坐标的精确测量。

2 基于光束法平差的多像空间前方交会

以图1中成像光束作为基本约束条件进行平差就是光束法平差。在给定初值的情况下，由于光束法平差对测量系统的所有参数：像点坐标、物方点坐标、像机内外方位参数、畸变参数等等进行整体绑定计算，使物方点重投影结果与实际像点之间的偏差最小，因而能够求得精确解［4］。如图2，以光束法平差整体求解空间物方点的三维坐标Pc（Xc，Yc，Zc），并以此为控制点进行多像空间前方交会。

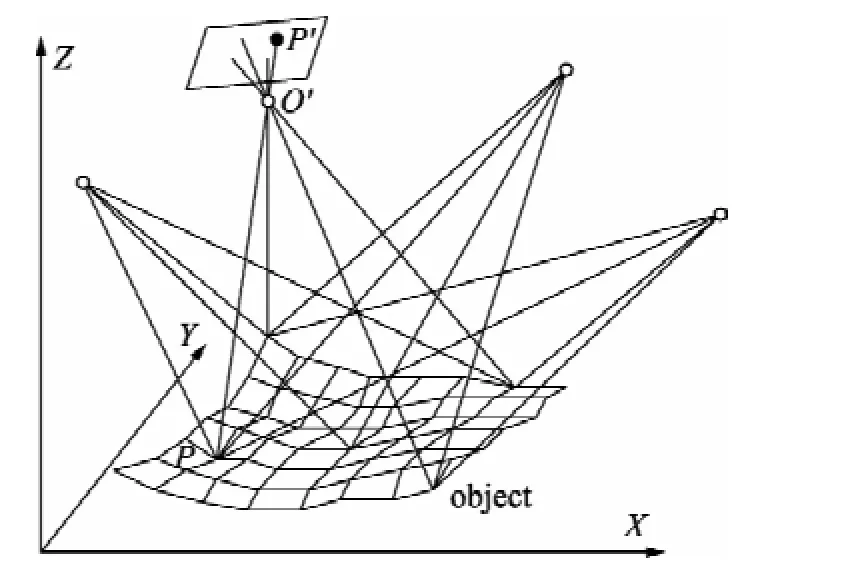
图1 多摄站空间交会

根据像点坐标误差方程式可以方便地求出物方点空间坐标M（X，Y，Z），其误差方程的一般形式为：

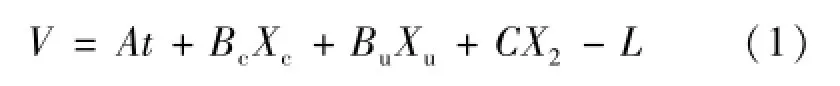
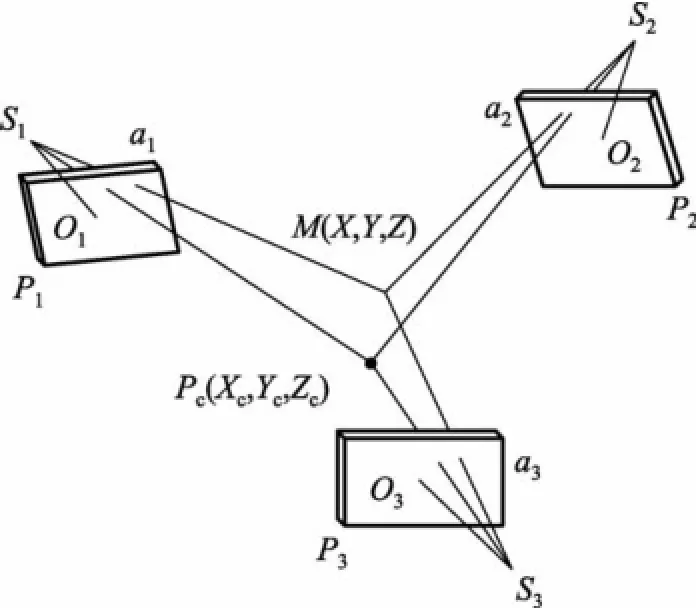
图2 多像空间前方交会示意图

式中：A、Bc、Bu、C为相应各阶偏导数，t为外方位元素的变化量，Xc为物方已知点（控制点）改正值，Xu为物方待定点改正值；X2为内方位元素变化量，L为迭代观察值。如果将控制点（通过近景摄影标准流程求得）视为真值，并且像机在测量开始前均通过自标定确定其内方位元素，其控制点三维坐标已知即t＝0，故X2＝0，控制点坐标视为真值即Xc＝0，这样像点误差方程变为：

式中：vx、vy为像点误差在像坐标系下的分量，a11，…，a23为像点坐标相对于摄影中心的偏导数，ΔX、ΔY、ΔZ为物方点M修正值，（x）、（y）分别为x、y前一次迭代运行的结果。线-线交会过程中，单台像机表示的方程有两个，而未知数X、Y、Z有3个，因而当摄像机≥2时，方程有解。本例摄像机数为3，物方点M分别在3台摄像机上的像点（a1，a2，a3），根据最小二乘原理，使像点坐标观测值的改正数的平方和最小，即：

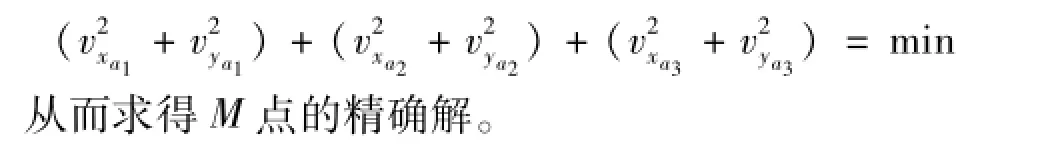
3 不同组像片的内方位元素修正

测量过程涉及多台（3台）像机同时工作。由于镜头的畸变、机身结构的变化等因素的影响，每台像机系统其内方位元素都不一样，即使同一像机不同时刻拍出的像片其内方位元素也是不一样的。文献［5］给出了考虑畸变情况下修正后的线性方程：

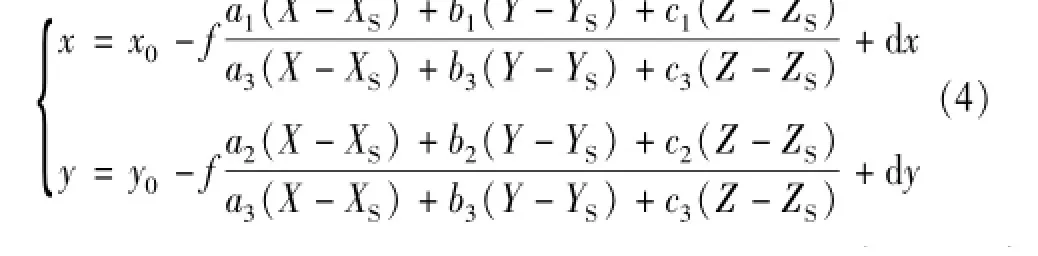
考虑到每组像片所涉及的像机内方位元素的变化，方程（4）又可以改写为：

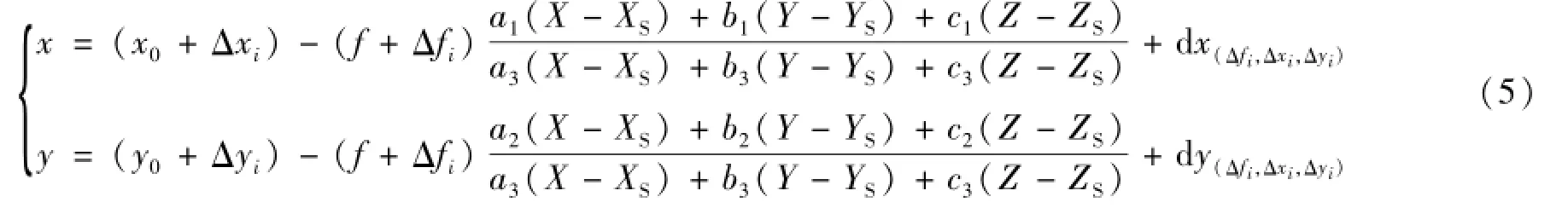
式中：x，y是像点坐标；X，Y，Z是物方点坐标；XS，YS，ZS是摄影中心的坐标；x0、y0为像主点坐标；Δx，Δy像差修正系数；ai，bi，ci（i＝1，2，3）是像空间坐标系相对于物空间坐标系的方向余弦；f为像机主距；Δxi、Δyi、Δfi（i＝1、2、3）为相应参数的微小变化量，其中i为不同像机序列。

对于多目视觉系统的标定，Fraser C S在单像机10参数法（x0，y0，f，K1，K2，K3，P1，P2，b1，b2）的基础上引入系统组合修正参数aij得到11参数法［6，7］，其方法同样适用于不同像机系统（机身、镜头不同）的自标定，从而为不同像机系统进行组网拍摄奠定了理论基础［8］。

4 系统硬件组成及测试过程

系统硬件基本配置包括：测棒、像机、镜头、同步拍摄装置，见图3。

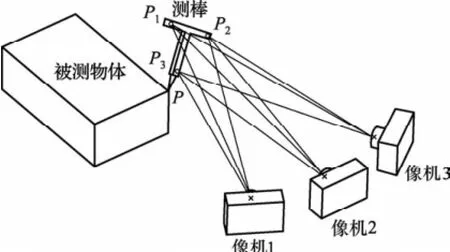
图3 三目近景摄影系统硬件组成

（1）测棒

单、双像机系统中，测棒上特征点需严格制作，除保证尺寸位置外，还必须确保能建立测棒坐标系，以完成坐标转换。新系统中测棒主要作用是单一的坐标传递，即依靠图4中的P1、P2、P3点的三维坐标来计算出P点的三坐标尺寸，不需要建立测棒坐标系来进行坐标变换。为了方便识别，将P1、P2、P3设计为直径为5 mm的白色圆点，见图5。

（2）像机型号为NIKON D300S，数量为3台。

图4 测棒

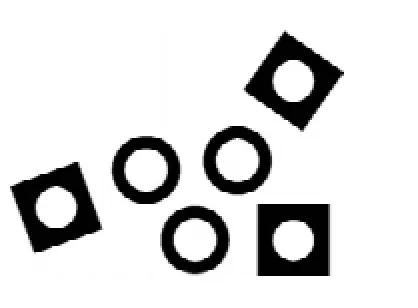
图5 非编码点

（3）镜头：3个24 mm非量测定焦镜头。

（4）同步拍摄设备：3套NIKON电子同步快门。由于测棒为人工手持测量，在拍摄过程中不可能长时间保持静止不动，因而需要3台数码像机同时拍摄测棒上的非编码点，得到同一时刻3个不同方位的像片。

首先在被测物体表面随机布置一定数量的编码点［9，10］，在合适的位置安放经过校验的比例尺（两端点含有绝对长度尺寸）。其次先用像机1以编码点和比例尺为依据进行现场自标定，确定像机1系统的内方位元素，接着对拍摄现场（此时不含测棒）进行不同视角的交向拍摄，完成一个近景摄影测量的标准流程［11］。接着对另外两台像机（像机2、像机3）进行现场自标定，按图3布置，确保3台像机能同时拍摄相同的区域。测棒的尖端P点置于被测点上，将测棒上有非编码点的一侧朝向3台像机，按下电子同步快门遥控器，同时触发3台像机，测棒在每一位置得到3幅照片。将像机1、2、3得到的像片分组输入光束平差软件中，根据不同像机系统的标定结果分别修正不同组像片内方位元素的附加参数，最后整体光束平差、全局优化并输出结果，图6为系统测量流程图。

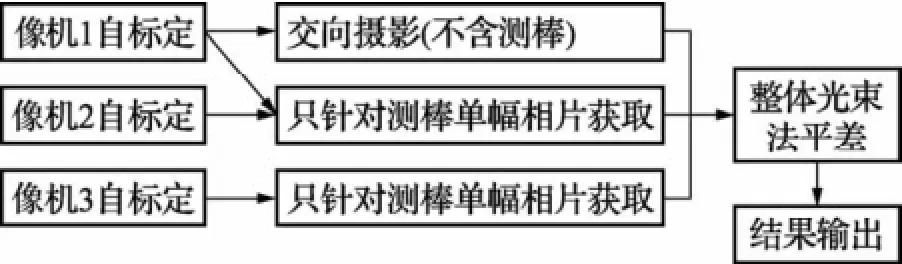
图6 系统测量流程图

5 系统精度测试

对新构建系统的精度测试，可按VDI／VDE 2634 PartI推荐的方法来进行检测［12］。测试系统尺寸自定，测量框架钢球的布置方位参见图7。

同一直线钢球间球心距通过计量型三坐标仪测得，并视为钢球间距离的真值，如表1所示。

图7 钢球布置示意图

表1 钢球距离三坐标测量值mm

对按图7布置的钢球使用测棒进行摄影测量，每采集1点需3像机系统同时拍照，获取3张像片。要得到一个球心的坐标需要在其表面测量3个位置共9幅像片。将像片输入GOM公司TRITOP 6.3.5软件，计算出各像机内方位元素及畸变修正参数，见表2。利用分组求解功能对所有像片进行基于全局优化光束平差算法的坐标解算，得到测棒上标识点P1、P2、P3的三维坐标尺寸，进而求得图4中P点的X，Y，Z。

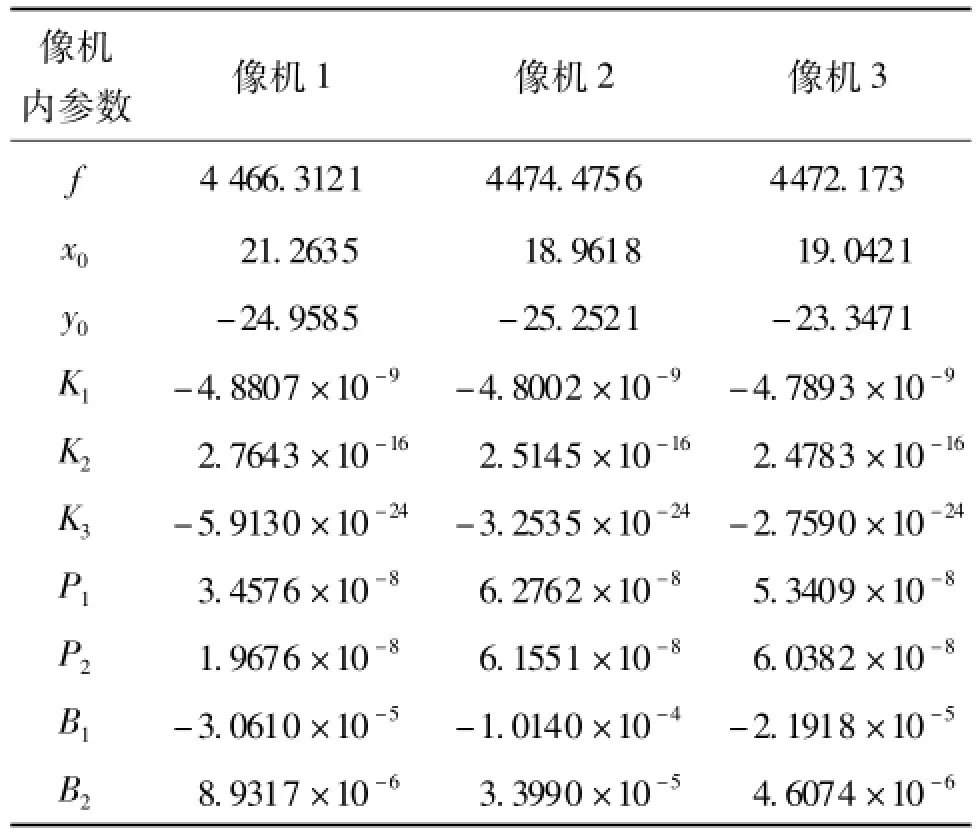
表2 各像机内方位元素及畸变修正参数pixel

表2中f为像机焦距，x0、y0为像主点坐标，K1、 K2、K3为径向畸变修正系数；P1、P2为切向畸变修正系数，B1、B2为仿射映射畸变修正系数。

按此方法分别测量7次，计算其算术平均值、标准差、极差及相对误差［13］，见表3。

由表3可知，3像机近景CMM系统的标准差最大值为0.0143mm，极差最大值为0.037mm，均小于0.05mm，这说明系统鲁棒性较好。相对误差范围为1.50958×10－5到3.44106×10－5，即相对测量精度范围由1∶29061到1∶66244，优于单像系统的1∶2000和双像系统的1∶20000。

将系统测量真值与相对误差进行比较，见图8。可以看出曲线具有下行趋势。随着测量距离的增加，测量的相对误差趋于减小。当测量物尺寸较小时，测量的相对误差较大，和双像机系统相比优势并不明显，随着被测物尺寸的增加，相对误差逐渐减小，测量距离948.351mm时，相对测量精度达1∶66244。随着测量距离的继续增加，相对测量精度有继续提高的趋势。

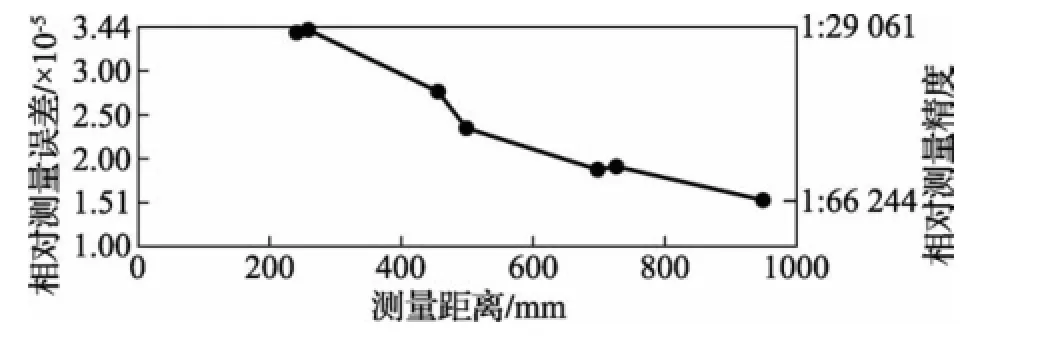
图8 相对误差／精度与测量值趋势图

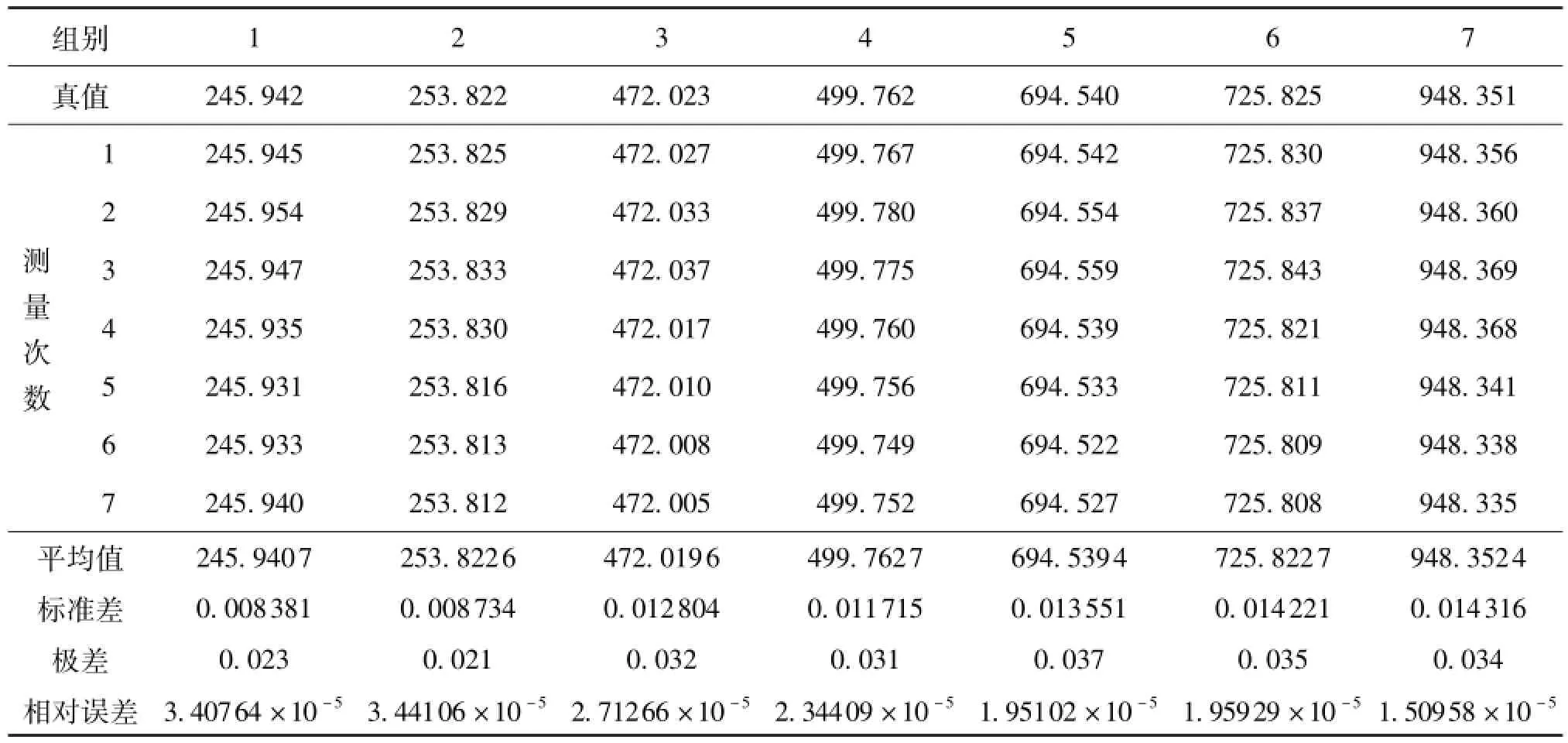
表3 数据对比分析mm

6 结 论

设计了一种新型的3像机单点测棒量测系统，通过3台数码像机系统同时对测棒进行拍照，获取3个方向上的像片，在各像机单独自标定的基础上，通过全局光束平差优化，实现测棒上P点的精确定位。和单、双像机测量系统相比，虽然系统增加了一到两套像机系统，但使用的测棒结构简单、制作成本低，更重要的是三像机测棒系统可以利用平差优化算法，提高了测量精度。实验表明，该系统测量精度优于单、双像机系统，同时随着测量尺寸的增加，系统精度呈上升趋势，说明系统具有良好的测量稳定性，适合中、大型尺寸间单点三坐标检测。

［1］ 黄桂平，叶声华，王保丰.单台相机三坐标测量的一种新方法［J］.仪器仪表学报，2005，26（9）：934－937.

［2］ Harley R，Zisserman A.Multiple view geometry in computer vision［M］.Cambridge：Cambridge University Press，2000.

［3］ Luhmann T.Close range photogrammetry princip les，techniques and applications［M］.London，UK：Whittles Publishing，2011.

［4］ 于起峰，尚洋.摄像测量学原理与应用［M］.北京：科学出版社，2009.

［5］ Tecklenburg W，Luhmann T，Hastedt H.Camera Modelling with Image-Variant Parameters and Finite Elements［C］／／Optical3-D Measurement Techniques V. Vienna，Austria，2001，328－335.

［6］ Fraser C S.Digital camera self-calibration［J］.ISPRS JournalofPhotogrammetryandRemoteSensing，1997，52（4）：149-159.

［7］ Fraser C S，Shortis M R，Ganci G.Multi-sensor system self-calibration［C］／／Photonics East′95.International Society for Optics and Photonics，Philadelphia，USA，1995，2－18.

［8］ Fraser C S，Kenneth L.Design and Implementation of a Computational Processing System for Off-Line Digital Close-Range Photogrammetry［J］.ISPRSJournalof Photogrammetry＆RemoteSensing，2000，55（2）：94－104.

［9］ 张维中，张丽艳，潘振宽.一种基于标记点的近景摄影测量系统［J］.东南大学学报（自然科学版），2006，36（5）：371－375.

［10］ Zheng JD，Zhang L Y.Accurate3D Target Positioning in Close Range Photogrammetry with Implicit Image Correction［J］.ChineseJournalofAeronautics，2009，22：649－657.

［11］ 邾继贵，于之靖.视觉测量原理与方法［M］.北京：机械工业出版社，2012.

［12］ VDI／VDE.VDI／VDE 2634 Part 1.Optical 3D Measuring Systems Imaging Systems with Point-by-point Probing［S］.Beuth Verlag，Berlin，2002.

［13］ 中华人民共和国国家质量监督检验检疫总局，中国国家标准化管理委员会.GB／T 12979—2008近景摄影测量规范［S］.2008.

New Method of Single Point3D Coordinate Measurement w ith Bund le Adjustm ent

RAN Xian-sheng1，2， ZHU Cai-chao1， LIN Li2
（1.The State Key Laboratory of Mechanical Transmission，Chongqing University，Chongqing 400044，China；
2.College of Mechatronics and Automobile Engineering，Chongqing Jiaotong University，Chongqing 400074，China）

Based on the research correction ofmulti-image interior orientation and integrated bundle adjustment，anew method is proposed to perform data collection of hand-held probing device by utilization of three cameras simultaneously and to achieve single point3D coordinationmeasurement by bundle adjustment，resulting in establishment of system hardware. During experiments，the relative accuracy of the new system is higher than 1∶29 061，compared to the measurement accuracy of the counterpartmetrology CMM device.This result is more accurate than that from single camera system or Duo-camera system，and could meet themeasurement requirements of industrial products.

Metrology；Bundle adjustment；Single pointmeasurement；Tri-cameras system；Probing device

TB92

A

1000-1158（2014）05-0409-05

10．3969／j．issn．1000-1158．2014．05．01

2013-09-11；

2014-01-10

国家自然科学基金（51375514）

冉险生（1971－），男，重庆人，博士研究生。主要从事三维数字化测量、工业近景摄影测量方面的研究。cqrxs＠qq.com