平面不规则结构弹塑性扭转振动效应敛散性研究

杨 杰 陆秀丽 虞终军

（同济大学建筑设计院（集团）有限公司，上海200092）

平面不规则结构弹塑性扭转振动效应敛散性研究

杨 杰*陆秀丽 虞终军

（同济大学建筑设计院（集团）有限公司，上海200092）

目前对平面不规则结构扭转振动效应研究集中于弹性阶段，对结构非弹性受力阶段的扭转效应控制缺乏明确的评价方法和指标。提出通过考察θr／u在弹塑性阶段的变化来对结构扭转振动响应进行评价，并以此为基础定义了结构弹塑性扭转振动效应的敛散性。采用PERFORM-3D对三种典型的结构平面布置进行弹塑性扭转振动效应敛散性计算，对计算结果进行对比分析，验证了敛散性分析对结构弹塑性扭转振动效应评价的有效性和必要性，并进一步对结构弹塑性扭转振动效应敛散性的主要影响因素进行简要分析。最后，探讨了敛散性指标作为结构的弹塑性扭转振动效应评价指标的合理性和优越性。

平面不规则结构，弹塑性，扭转振动效应，敛散性

1 引 言

近年来，各种复杂体型和平面不对称、不规则结构的多高层建筑不断涌现，使得地震作用下的扭转振动效应越来越成为不规则建筑结构抗震设计中的焦点问题。然而，对不规则结构的扭转振动效应研究还存在着很多没有被完全解决的关键问题，尤其是对结构弹塑性阶段扭转振动效应的研究和评价还处于较为初级的阶段，随着抗震设计日益向精确化、性能化的方向发展，有必要对结构弹塑性扭转振动效应进行更深入的研究和探讨，从而为不规则结构抗震设计提供更明确和科学的指导。

2 现行结构扭转振动效应评价指标

现有的结构扭转振动效应研究成果主要集中于结构的弹性阶段，取得了丰硕的成果，并以扭转控制指标的形式指导抗震设计［1］。我国规范主要通过结构弹性阶段的位移比和周期比控制结构的扭转振动反应，根据文献［2］，在考虑偶然偏心影响的地震作用下，楼层竖向构件的最大水平位移和层间位移之比，A级高度高层建筑不宜大于该楼层平均值的1.2倍，不应大于该楼层平均值的1.5倍；B级高度高层建筑，混合结构高层建筑及复杂高层建筑不宜大于平均值的1.2倍，不应大于该楼层平均值的1.4倍。同时，对于结构的平扭周期比，规范也有明确的要求。

对于非弹性阶段的扭转效应控制，上述指标难以完全适用。在非弹性阶段，结构的刚度处于动态变化过程中，且侧向刚度和扭转刚度的退化并非线性关系，相应结构位移与位移比的变化并不同步，某一时刻的静态位移比难以反映结构的扭转振动特性，因此弹性阶段位移比的限值未必适用于非弹性阶段；而周期比即使对弹性阶段扭转振动效应的控制也相对间接和不全面，在非弹性阶段，并不适于作为一个主要的扭转控制指标。

近年来，随着计算机硬件和软件的快速发展，对结构进行各种工况下全面弹塑性分析越来越方便。因此，对于结构在非弹性阶段的扭转振动效应，有必要也有可能以一种更直接和全面的指标来评价和控制。

3 弹塑性扭转振动效应的敛散性的定义

根据文献［3］，结构顶部相对扭转振动响应可以用θr／u来表达（θ，r分别为扭转角和结构的回转半径，u为质心平动位移）。这个指标是一个结果型的指标，直接反映了结构的扭转振动响应，在非弹性阶段也应是同样适用的。但长期以来，对于θr／u作为扭转控制指标在弹塑性阶段的限值缺乏研究和共识，因此难以直接采用。鉴于此，本文建议通过考察θr／u在弹塑性阶段的变化来对结构扭转振动响应进行评价，以根据现行规范设计的结构在弹性阶段的θr／u作为起点，研究θr／u在弹塑性阶段的变化规律。

若结构在弹塑性阶段的θr／u总体呈现不断上升的趋势，则将其定义为扭转发散型结构；反之，则为扭转收敛型结构。显然，在抗震设计中，扭转收敛型结构代表了更好的抗震性能，因为θr／u不断下降意味着，结构振动的扭转成分呈下降趋势，结构的扭转效应在塑性阶段将不会是引起结构破坏的主要因素。对于扭转收敛型结构，弹性阶段的抗扭设计对于塑性阶段总体是偏安全的。而扭转发散型结构进入非弹性阶段后，其扭转效应有一个持续发展强化的过程，具有一定不确定性，应尽力避免。对于扭转发散型结构，弹性阶段的抗扭设计很有可能是不够的，如实在无法避免，就应进行深入分析，并进一步加强弹性阶段的抗扭设计，使其也能满足塑性阶段的需求。

平面不规则结构在弹性阶段由于质量中心和刚度中心的不重合导致平扭耦联反应，从而使结构构件的变形需求分布在结构平面内并不一致；而在非弹性阶段，受到结构的材料和几何非线性不断发展的影响，结构刚度不断不均匀退化和重分布，构件变形需求的不一致性往往与弹性阶段有着很大区别。这种区别可以通过θr／u的变化显现出来，从而成为我们抗扭设计考虑的重要因素。

不同类型的不规则结构弹塑性扭转振动响应有着不同的特点和规律，下面对几种典型结构类型的弹塑性扭转振动响应进行一些分析和探讨。

4 几种典型结构形式的弹塑性扭转振动效应敛散性分析

4.1 分析软件介绍

本文采用PERFORM-3D作为主要的弹塑性分析工具，PERFORM-3D主要用于对结构进行抗震分析和性能化评估，其分析结果的得到了国际学术界和工程界的广泛认可，尤其擅长分析错综复杂的剪力墙体系，能够提供较为准确的动力弹塑性分析功能。

采用考虑强度损失的三折线模型（图1）定义混凝土材料的本构关系，采用两折线模型定义钢材的本构关系（图2），通过定义基于应变的耗能指标，来考虑材料在循环加载过程中的刚度退化。

图1 混凝土材料本构关系Fig.1 Concretematerial constitutive relationship

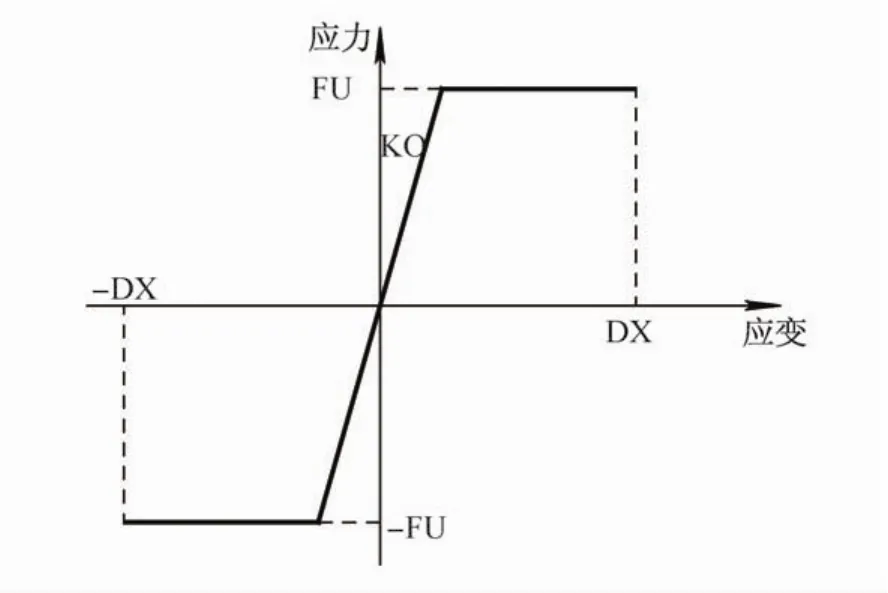
图2 钢筋材料本构关系Fig.2 Steelmaterial constitutive relationship

模型中的框架梁及连梁的弹塑性模型由中间的弹性杆、两端的塑性弯曲铰和剪切强度截面组成（图3）。框架柱的弹塑性模型由中间的弹性杆和两端的纤维截面组成，采用纤维截面模拟剪力墙的弹塑性弯曲破坏，并定义相应的非线性剪切材料来模拟剪力墙的弹塑性剪切破坏特性。框架柱和剪力墙中的纤维截面通过直接读取材料的弹塑性参数来实现对相应构件弹塑性变形的模拟。在剪力墙中设置内嵌梁，以确保连梁与剪力墙单元的弯矩连续传递。输入时间间隔均为0.02 s，持续时间均为20 s。建筑结构的阻尼比为0.05。

4.2 基本对称框筒

常规设计的框架-筒体结构，其核心筒均为居中布置，而框架则沿四周布置，该结构体系平面上对称规则，刚度中心与质量中心基本重合，具有合理的地震作用传递途径，因而在实际工程中被普遍采用。下面对一典型的框架-筒体结构做弹塑性扭转振动效应敛散性分析。某高层办公楼，层高4.8 m，地上18层，总高86.4 m，设防烈度8度，设计基本地震最大加速度值0.2 g，场地类别Ⅱ类。结构的弹性模型采用PKPM-SATWE（2012年版）建模和计算，考虑5%的偶然偏心，标准层平面图见图4，主要计算结果详见表1，均满足现行规范的各项要求，导入PERFORM-3D后结构的前三阶周期为1.88 s、1.87 s、1.51 s，与SATWE计算结果基本保持一致。

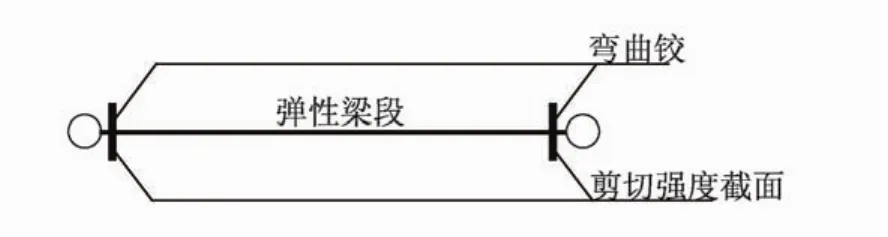
图3 框架梁弹塑性模型Fig.3 Frame beam elasto-plastic model

本文分析基于结构未发生严重剪切破坏的基础上，由于剪切破坏带有脆性特征，发生严重的剪切破坏将使后续分析失去意义。因此，应通过构造措施，使结构主要构件处于剪切弹性状态。

在PERFORM-3D中，采用对主要构件设置剪切强度截面并计算其需求能力比的方法控制其剪切强度满足要求。

计算分析共采用3条地震波，均为二类场地波，分别是El Centro波，唐山波和兰州波；前两条为天然波，后一条为人工波。每条波均考虑双向地震作用，两个方向的最大地震加速度按1∶0.85的比例调整。为便于分析，每条地震波按小震至大震的顺序依次分为五个分析工况，其对应的地震加速度时程最大值分别为70 cm／s2、152.5 cm／s2、235 cm／s2、317.5 cm／s2、400 cm／s2。地震波计算

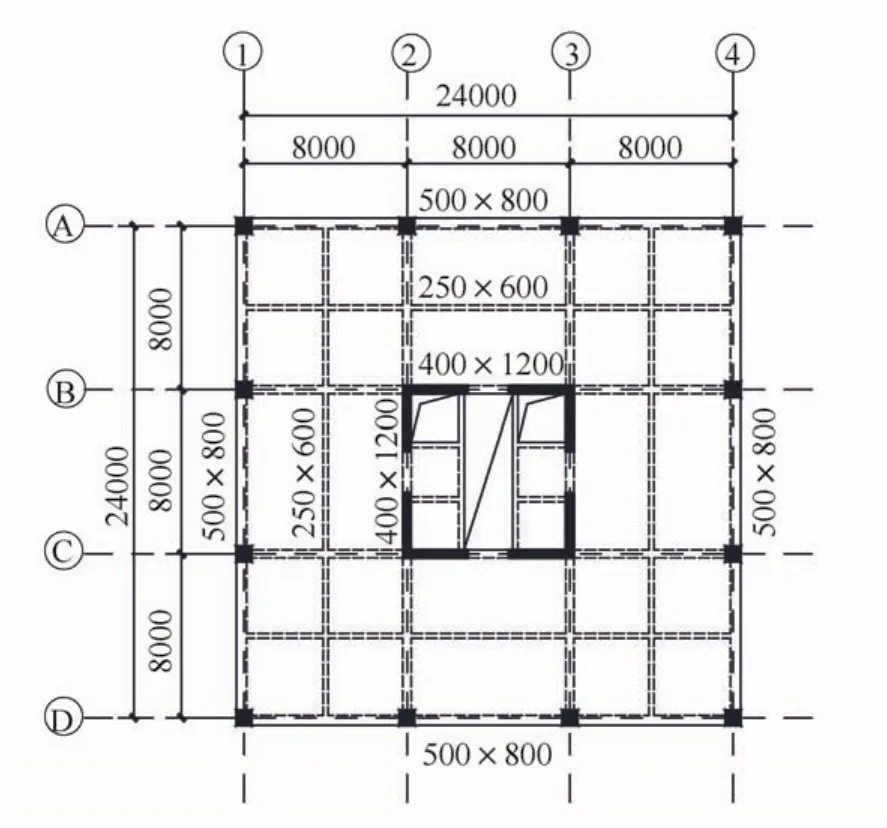
图4 典型楼层平面图（单位：mm）Fig.4 Typical structural plan（Unit：mm）

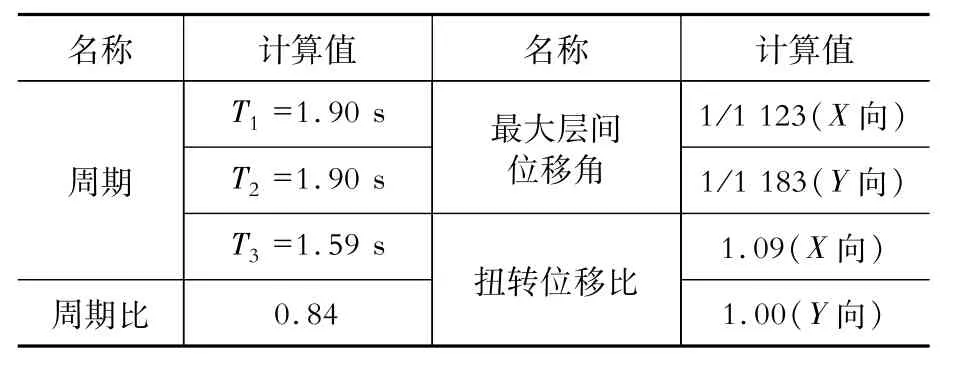
表1 SATWE弹性计算总信息Table 1Prelim inary results of the SATWE analysis

选用前述三条地震波对其进行弹塑性分析，采用自编数据处理程序CTE1.0对其节点质量和位移结果文件进行提取和分析，绘出其多工况θr／u时程曲线（图5—图7）。将每个分析工况的θr／u最大值取绝对值后进行连接，即得到了结构的弹塑性扭转振动效应敛散性曲线（图8）。

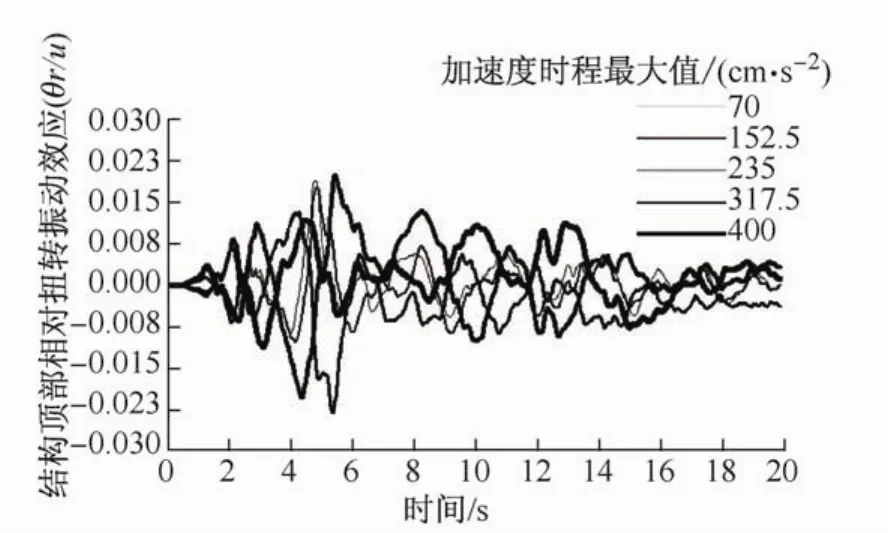
图5 结构顶部相对扭转效应时程曲线（El Centro波）Fig.5 Time histories of the elasto-plastic torsional effect at the building top（El CentroWave）

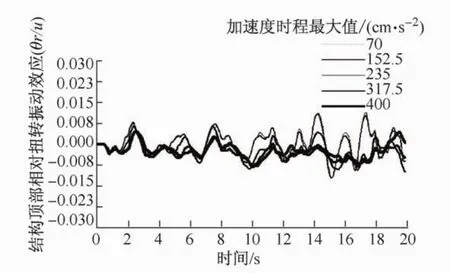
图6 结构顶部相对扭转效应时程曲线（唐山波）Fig.6 Time histories of the elasto-plastic torsional effect at the building top（Tangshan Wave）

图7 结构顶部相对扭转效应时程曲线（兰州波）Fig.7 Time histories of elasto-plastic torsional effect at the building top（Lanzhou Wave）

由图8可知，在5%的偶然偏心条件下，典型框架-筒体结构弹塑性扭转振动效应总体是收敛的，结合图9结构的塑性铰发展历程可知，随着地震作用的加强，结构核心筒连梁首先屈服，连梁协调变形能力下降，联肢墙的受力体系快速退化为独立墙肢受力，核心筒整体抗侧刚度下降较快，而外围框架体系虽然也出现塑性铰，但个别构件的屈服对体系的整体刚度影响并不显著，结构体系外圈刚度相对于内圈刚度有所上升，结构的振动趋向于平动。因此，结构的相对弹塑性扭转振动效应总体呈下降趋势。

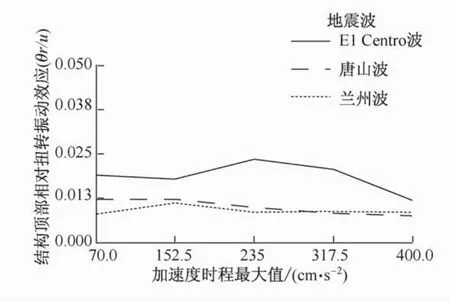
图8 结构的弹塑性扭转振动效应敛散性曲线Fig.8 Convergence curves of elasto-plastic torsional effect

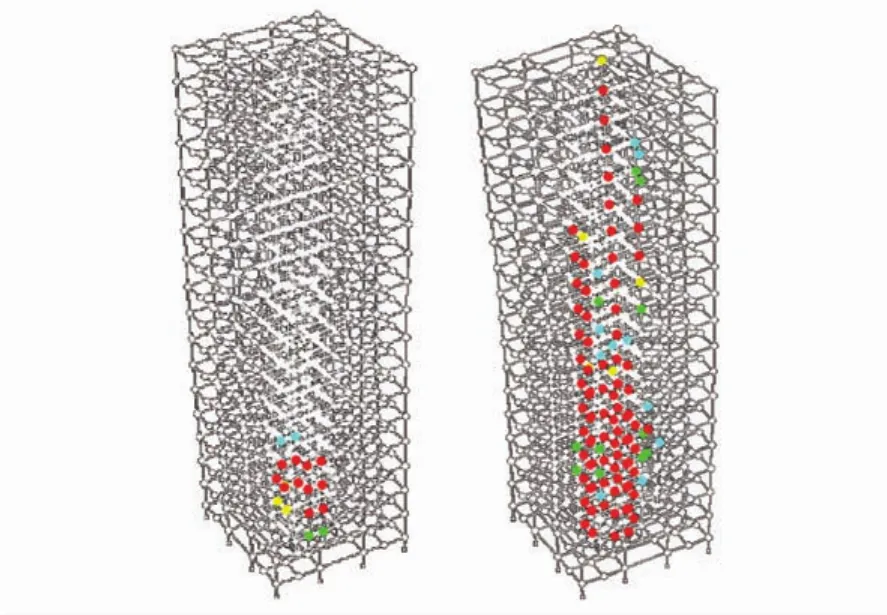
图9 结构典型梁塑性铰发展历程（唐山波）Fig.9 Typical development of the beam plastic hinges（Tangshan Wave）

由上述分析可知，现行规范强调通过连梁的屈服耗能并实现结构的第二道防线，这也导致了按规范设计结构的弹塑性刚度重分布朝着对抗扭有利的方向发展，因此合理设计的框架-筒体结构普遍具有较好的弹塑性抗扭性能。这一点在实际地震中也屡有印证，如1985年的墨西哥地震中，采用外框内筒结构的十八层美洲银行大厦，只受到了轻微破坏，而周围有大量建筑物由于结构扭转发生破坏。此外，适当加强体系外围框架的抗侧刚度对于结构弹性和塑性阶段的抗扭都是很有必要的。

4.3 偏置筒体

偏置筒体在建筑上有其合理的一面，常常能将竖向交通和附属用房部分集中置于朝向较差方位，使办公区获得较好的朝向和景观效果，并容易获得更灵活的房间分割布置。但由于其偏心距较大，结构扭转效应明显，因此有必要对其弹塑性扭转效应作更深入的研究和探讨。

某偏置筒体高层商务楼，标准层高5 m，地上25层，总高125 m，设防烈度8度，设计基本地震最大加速度值0.2 g，场地类别Ⅱ类。标准层平面图见图10，加速度时程沿X向输入，分析方法同上节框筒结构，不再赘述。图11—图13是其顶部相对扭转振动效应时程曲线，图14是该模型的弹塑性扭转振动效应敛散性曲线。

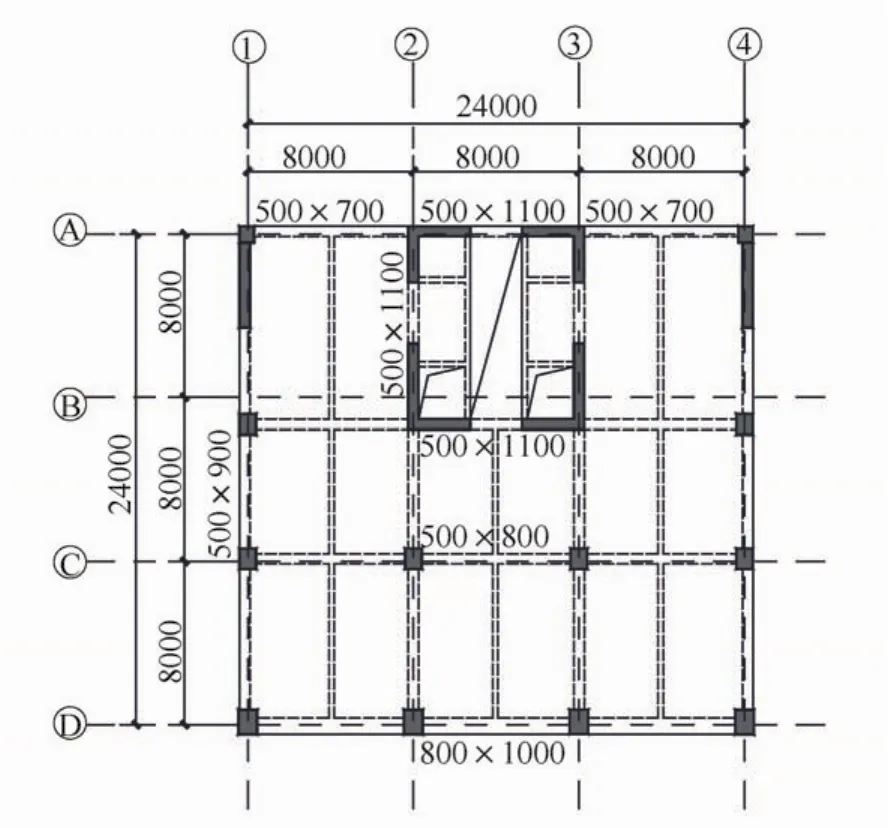
图10 典型楼层平面图Fig.10 Typical structure plan

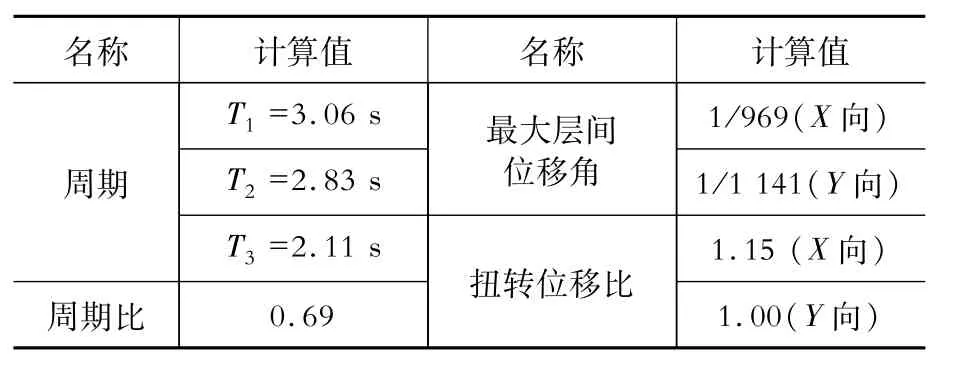
表2 SATWE弹性计算总信息Table 2Prelim inary results of the SATWE analysis

由图14可见，结构在弹塑性发展过程中的扭转效应在小震至大震阶段总体呈发散趋势，结合结构的塑性铰发展历程可知，由于筒体位于结构外侧，因此其抗侧刚度的快速退化直接导致了相对抗扭刚度的下降，结构扭转振动的趋势不断加强，扭转效应呈发散趋势。

由上述分析可知，与对称框筒不同，偏置筒体由于初始偏心距较大，按静力计算结果进行设计时，往往依靠在周边设置强大的抗扭转墙体使其满足位移比和周期比的要求，进入非弹性阶段后，随着外围墙体刚度不断退化，其对扭转振动的限制能力减弱，体系在弹性阶段的静态扭转平衡在进入非弹性阶段后有可能被打破，并在某一阶段持续发展，弹性拟静力分析对偏置筒体的扭转效应往往估计不足，因此对于偏置筒体的抗扭设计，宜进行弹塑性阶段的校核和验算。

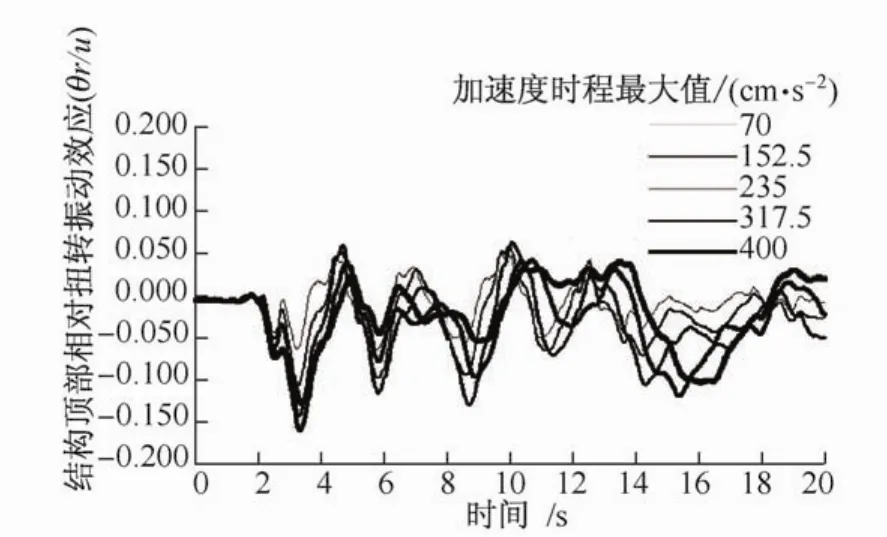
图11 结构顶部相对扭转效应时程曲线（El Centro波）Fig.11 Time histories of the elasto-plastic torsional effect at the building top（El CentroWave）

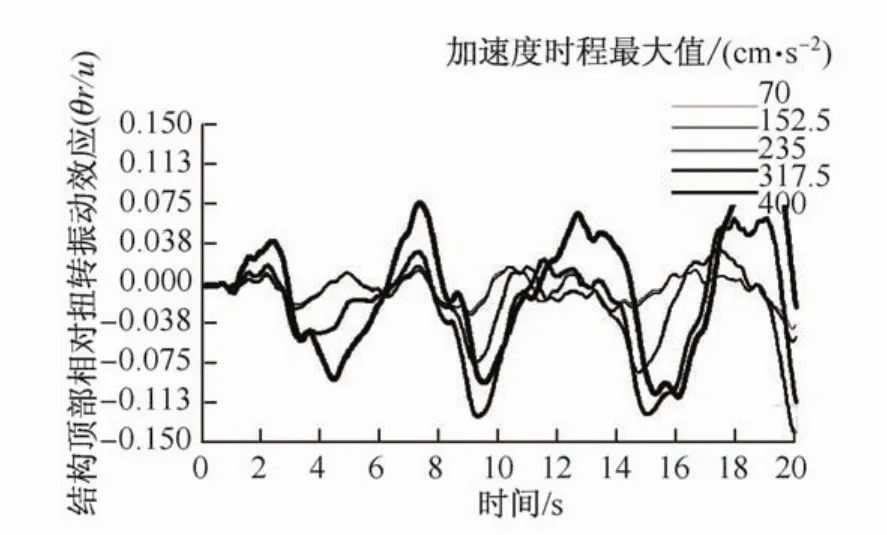
图12 结构顶部相对扭转效应时程曲线（唐山波）Fig.12 Time histories of the elasto-plastic torsional effect at the building top（Tangshan Wave）

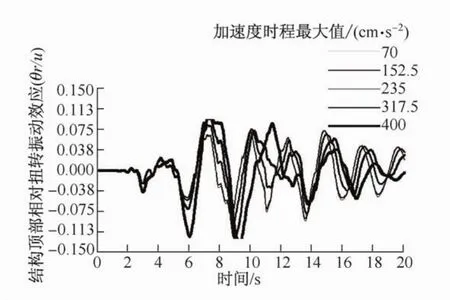
图13 结构顶部相对扭转效应时程曲线（兰州波）Fig.13 Time histories of elasto-plastic torsional effect at the building top（Lanzhou Wave）

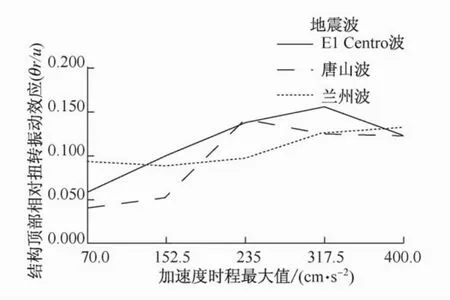
图14 结构的弹塑性扭转振动效应敛散性曲线Fig.14 Convergence curves of elasto-plastic torsional effect

4.4 任意平面不规则结构

对于任意平面不规则结构，均可用前述方法分析其弹塑性扭转的敛散性。以某“L”形高层办公楼为例，标准层高4.5 m，地上22层，总高100 m，场地条件同前。结构沿Y向初始偏心约5%，标准层平面图见图15，导入PERFORM-3D后结构的前三阶周期为2.43 s、2.32 s、1.93 s，与SATWE计算结果基本保持一致。加速度时程沿X向输入，图16是该模型典型顶部相对扭转振动效应时程曲线，图17是该模型的弹塑性扭转振动效应敛散性曲线。

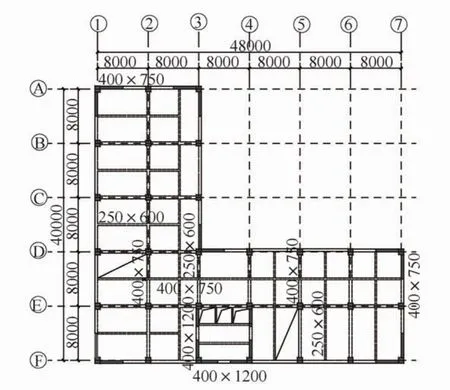
图15 典型楼层平面图Fig.15 Typical structure plan

由图17可见，结构在弹塑性发展过程中的扭转效应总体快速收敛，结合结构的塑性铰发展历程可知，由于结构南侧电梯筒体刚度较大，结构在弹性阶段刚心偏于南侧，进入弹塑性阶段后，南侧

由上述分析可知，设计较合理的小偏心率“L”形平面结构，依然具备较好的弹塑性抗扭转性能。扭转振动效应受到多种因素影响，某些因素进入塑性阶段后才会逐渐显现，因此有必要对于不规则结构扭转振动效应敛散性进行具体分析以确定其在某一阶段扭转振动特性。电梯筒体连梁首先屈服，其抗侧刚度的快速退化直接导致了结构偏心距逐渐减小，结构的振动更趋向平动。

表3 SATWE弹性计算总信息Table 3Prelim inary results of the SATWE analysis

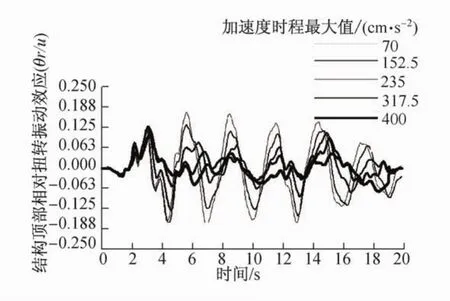
图16 结构顶部相对扭转效应时程曲线（El Centro波）Fig.16 Time histories of the elasto-plastic torsional effect at the building top（El CentroWave）

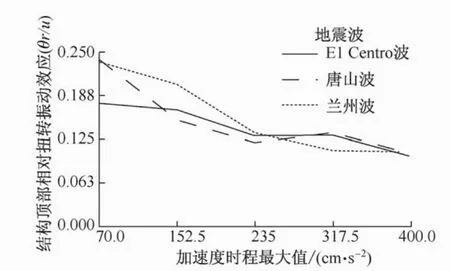
图17 结构的弹塑性扭转振动效应敛散性曲线Fig.17 Convergence curves of elasto-plastic torsional effect

5 结构弹塑性扭转振动效应敛散性的影响因素简析

结构的扭转振动效应是结构刚度特性与质量特性共同作用的结果。进入非弹性阶段以后，结构刚度特性处于持续变化的状态中；其刚度特性的变化主要由结构材料非线性和几何非线性引起；对于混凝土结构，以前者为主。

结构刚度特性的变化主要表现为结构相对和绝对抗扭刚度的变化（4.1、4.2节算例）、结构相对偏心距的变化（4.3节算例）、以及由于结构自振特性变化引起的振型耦联状态的变化，上述几个因素的共同作用构成了结构弹塑性扭转振动效应敛散性的主要影响因素。此外，结构动力荷载形式、加载路径以及结构阻尼的非线性特征也对扭转振动效应敛散性有一定影响。

6 结 论

本文主要对平面不规则结构的弹塑性扭转振动效应的敛散性进行研究和分析，并得出以下体会和探讨：

（1）结构在非弹性阶段的扭转振动效应与弹性阶段既有联系又有所区别，弹性阶段的刚度特性是向非弹性阶段退化的起点，基于结构自身的非线性特性，弹性阶段的扭转平衡或不平衡进入非弹性阶段后都有可能发生变化，这种变化可用弹塑性扭转振动效应敛散性曲线来衡量和判别。

（2）平面不规则结构进入非弹性阶段后，其不规则性引起的扭转效应有可能逐渐被释放，因此，对其进行扭转振动效应敛散性分析是有必要的。

（3）结构的弹塑性扭转振动效应敛散性是结构自身多种非线性特性的综合反映。不同类型的平面不规则结构，在不同的场地、荷载、阻尼工况条件下的表现应具有不同的特点，前述4.1—4.3节算例仅为例证性分析，对不同类型结构扭转振动效应敛散性规律的总结有待于基于更多工程实例的深入研究。

（4）结构的弹塑性扭转振动效应敛散性是结构的固有特性，是结构动力规则性的一种体现。对其进行研究，有助于我们更好地掌握结构的性能，更准确地评估其在地震作用下表现。目前，结构的性能化设计向指标化、精确化的方向发展；相关规范中已对结构构件的性能化指标有所规定，结构的弹塑性扭转振动效应敛散性指标可以作为结构的一个整体扭转性能指标，成为性能化设计的一部分。

（5）采用扭转振动效应敛散性指标对结构的弹塑性扭转振动效应进行评价，有利于实现结构弹性阶段和非弹性阶段设计分析的自然衔接。既是对弹性阶段设计的校核与验证，也是弹性阶段设计的补充与延续。

［1］ 中华人民共和国住房和城乡建设部.GB 50011—2010建筑抗震设计规范［S］.北京：中国建筑工业出版社，2010.Ministry of Construction of the People’s Republic of China.GB 50011—2010 Code for seismic design of buildings［S］.Beijing：China Architecture and Building Press，2010.（in Chinese）

［2］ 中华人民共和国住房和城乡建设部.JGJ 3—2010高层建筑混凝土结构技术规程［S］.北京：中国建筑工业出版社，2010.Ministry of Construction of the People’s Republic of China.JGJ 3—2010 Technical specification for concrete structures of tall buildings［S］.Beijing：China Architecture and Building Press，2010.（in Chinese）

［3］ 徐培福，黄吉峰，韦承基.高层建筑结构在地震作用下的扭转振动效应［J］.建筑科学，2000，16（1）：1-6.Xu Peifu，Huang Jifeng，Wei Chengji.Response of torsional vibration of tall building structures induced by seismic action［J］.Building Science，2000，16（1）：1-6.（in Chinese）

［4］ 王墩，吕西林.平面不规则结构非弹性扭转地震反应研究进展［J］.地震工程与工程振动，2010，（4）：51-58.Wang Dun，Lu Xilin.Progress in study on inelastic torsional seismic response of asymmetric buildings［J］.Journal of Earthquake Engineering and Engineering Vibration，2010，（4）：51-58.（in Chinese）

［5］ 洪婷婷.浅析框架-核心筒结构设计中的几个问题［J］.结构工程师，2010，（8）：15-20.Hong Tingting.Analysis of some issues for design of frame-shearing wall structures［J］.Structural Engineers，2010，（8）：15-20.（in Chinese）

［6］ 孟春光，陆秀丽，耿耀明，等.某超高层抗震性能化设计及弹塑性时程分析［J］.结构工程师，2012，（4）：74-79.Meng Chunguang，Lu Xiuli，Geng Yaoming，et al.Performance based seismic design and dynamic elasto-plastic analysis of a super high-rise building［J］.Structural Engineers，2012，（4）：74-79.（in Chinese）

Convergence Study of the Elasto-plastic Torsional Effect in Asymmetric Buildings

YANG Jie*LU Xiuli YU Zhongjun
（Architectural Design and Research Institute of Tongji University（Group）Co.Ltd.，Shanghai200092，China）

Current studies of the torsional vibration effect in symmetric buildings focus on the elastic stage and there is no clear evaluation methods or index for inelastic torsional effect control.This paper proposed a method to evaluate torsional vibration effect by investigating variation ofθr／u.A convergence index of elastoplastic torsional effect in asymmetric buildingswas also defined.Torsional vibration effect convergence calculation was finished for three typical buildings by using PERFORM-3D.Calculation resultswere analyzed to verify the necessity and effectiveness of convergence index.A brief analysis on main factors of convergence index was carried out.Finally，the rationality and superiority of convergence index as a structural elasto-plastic torsional vibration effect evaluation index were discussed.

asymmetric building，elasto-plastic，torsional vibration effect，convergence

2013－08－20

*联系作者，Email：tjad＿yj＠163.com