斜拉空间桁架结构在静力作用下受力性能研究

王 鑫 汪长林 闫振国

（1.华中科技大学武昌分校，武汉430064；2.湖北华兴建筑有限公司，武汉432200；3.湖北鸿业建筑设计有限公司，武汉430056）

斜拉空间桁架结构在静力作用下受力性能研究

王 鑫1，*汪长林2闫振国3

（1.华中科技大学武昌分校，武汉430064；2.湖北华兴建筑有限公司，武汉432200；3.湖北鸿业建筑设计有限公司，武汉430056）

利用有限元分析软件ANSYS计算了某斜拉空间桁架在静力作用下的内力及自由端位移，归纳了内力系数与节间位置、预应力、斜拉索高度之间的函数关系；详细分析了斜拉索施加的初始预应力和斜拉索高度对该结构内力及自由端位移的影响，提出了斜拉空间桁架的临界预应变概念，回归出了自由端位移与初始预应变以及斜拉索高度的函数关系。本文的研究成果能够为斜拉空间结构的受力性能研究和工程实践提供指导。

斜拉空间桁架结构，静力荷载，有限元分析，临界预应变，内力系数

1 引 言

自20世纪50年代末建筑师们将斜拉桥的结构体系引入到建筑结构中之后，斜拉空间结构这一结构体系得到了空前的发展。当前，斜拉空间结构在我国得到了广泛的应用，机场大厅、体育场馆、展览中心等到处都能见到这一结构形式［1］。本文系统介绍了斜拉空间桁架受力分析理论与方法，详细分析了斜拉空间桁架结构在静力作用下内力及自由端位移分布规律并得出内力系数与节间位置、预应力以及斜拉索高度之间的函数关系，分析了该种结构在静力作用下的受力性能。

2 空间桁架受力分析基本理论

空间桁架与平面桁架同属一类结构，各结点均为理想铰，结构只承受结点力。由于空间桁架结构的每一个结点增加了一个自由度，故每一个结点的力向量和位移向量有三个分量［2］。

2.1 单元刚度矩阵的确定

整体坐标下的单元结点力向量和单元结点位移向量存在如下关系：

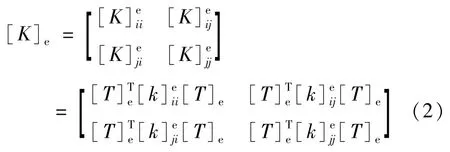
式中，［K］e为整体坐标单元刚度矩阵。采用φ325×12的无缝钢管，腹杆采用φ159×8的无缝钢管，上、下弦杆的弹性模量为E＝2.06×105N／mm2；拉索为高强钢丝录弹性模量E＝1.74×105N／mm2，极限延伸率为3%，截面积A＝1 256 mm2，极限抗拉强度为1 570 MPa，密度为7 850 kg／m3。本文采用ANSYS中的Link8和Link10单元分别模拟空间桁架的杆件和斜拉索［3，4］。

将［T］e及局部坐标各单元刚度子矩阵代入可得到整体刚度矩阵［K］e，各子矩阵为

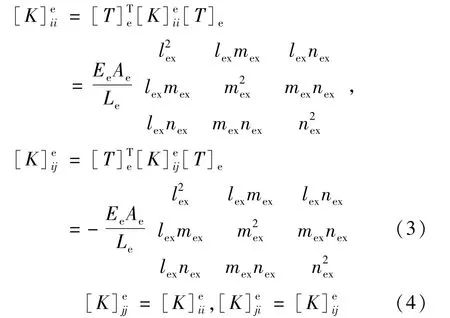
本文主要从两个方面的变化来进行研究：一是对斜拉索施加不同的预应力，本文采用的是初始预应变法（初始预应变为0，0.000 2，0.000 4，…，0.002共11种情况）；二是斜拉索上端高差变化（h＝12m、15m、18m、21m、24m、27m及30m 7种情况）。本文选用经典的双线性随动强化（BKIN）材料模型，它适用于各向同性材料的小应变问题。

1）斜拉索垂度效应

斜拉索垂度效应引起的非线性影响用Ernst公式［5］得出的等效弹性模量考虑，即考虑索力对其弹性模量的影响，等代弹性模量的计算公式如下：

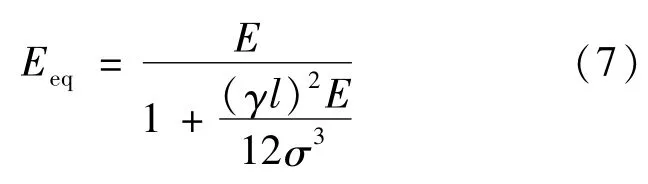
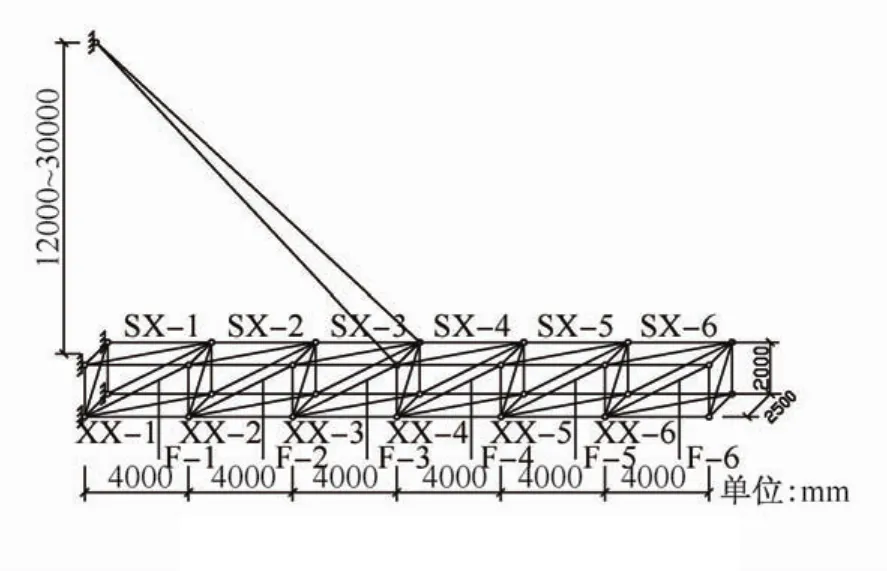
图1 斜拉空间桁架计算模型Fig.1 Cable-stayed spatial truss calculationmodel

其中：

2.2 单元内力的确定

结构整体平衡方程为

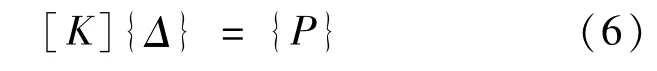
式中，｛P｝和｛Δ｝分别为结构结点荷载向量和结点位移向量，通过引入边界约束条件即可求得各结点位移。

3 斜拉空间桁架的计算模型

3.1 结构模型及参数

本文采用的空间桁架为四边形截面，高2 m，宽2.5 m，长24 m。图1中SX、XX、F分别代表上弦杆、下弦杆和腹杆，两根斜拉索下端分别铰接于桁架中部的两个上弦节点，上端则铰接于立柱。空间桁架一共6个节间，每个节间4 m，上、下弦杆

式中，Eeq为等效弹性模量；E为索的弹性模量；γ为索的比重；σ为索的拉应力；l为索的水平投影长度。

式（7）中的Eeq与l及σ呈非线性关系，因此Eeq的计算过程是一个逐次迭代的过程［6］。

2）斜拉索预应力值

斜拉索预应力值的选取，目前尚无统一规定，主要是参照桥梁方面的取值［7］。式中，［σ］为拉索的容许应力；Rb为拉索抗拉标准强度。

考虑到斜拉索在长期荷载作用下的松弛影响，斜拉索的最终应力不应超过0.45倍抗拉极限应力。本文中的最大预应力小于此值［7］。

3.2 荷载取值及非线性求解技术

静力荷载作用时桁架的每个上弦节点承受55 kN的节点荷载。ANSYS程序通过使用Newton-Raphson平衡迭代及弧长方法，来达到稳定的收敛。

3.3 斜拉空间桁架在静力作用下力学性能研究

3.3.1静力作用下自由端的位移

此空间桁架悬臂时在静力荷载作用下自由端的最大竖向位移为－13.98 cm，垂跨比为1／170。由表1可知：当在此空间桁架的中部加了斜拉索后即使不施加预应力，其自由端的最大竖向位移为－10.1 cm，垂跨比为1／240；当给斜拉索施加0.002的初始预应变时，其自由端的最大竖向位移为－4.64 cm，此时的垂跨比为1／510，远小于悬臂和未施加预应力的情况。为18 m时自由端位移最小，小于18 m时单调递减，大于18 m时单调递增。

（2）当初始预应变0.000 6＜ε≤0.001 2，斜拉索高度为21 m时自由端位移最小，小于21 m时单调递减，大于21 m时单调递增。

（3）当初始预应变ε＞0.001 2，随着斜拉索高度的增加自由端位移单调递减，且随着斜拉索高度的增加这种影响越来越小。就本桁架而言，斜拉索高度为21 m，初始预应变为0.001 2比较理想。

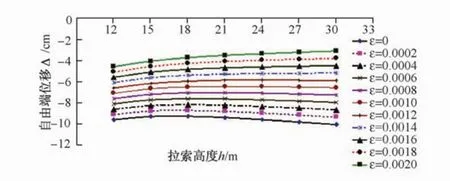
图2 自由端位移Δ-（拉索高度）h-（初始预应变）ε曲线Fig.2 Free end displacementΔ-（cable-stayed height）h-（initial prestrain）εcurve

3.3.2 静力作用下下弦杆内力

表2为斜拉索高度h＝12 m和30 m时对应于不同的预应力桁架下弦杆的内力。

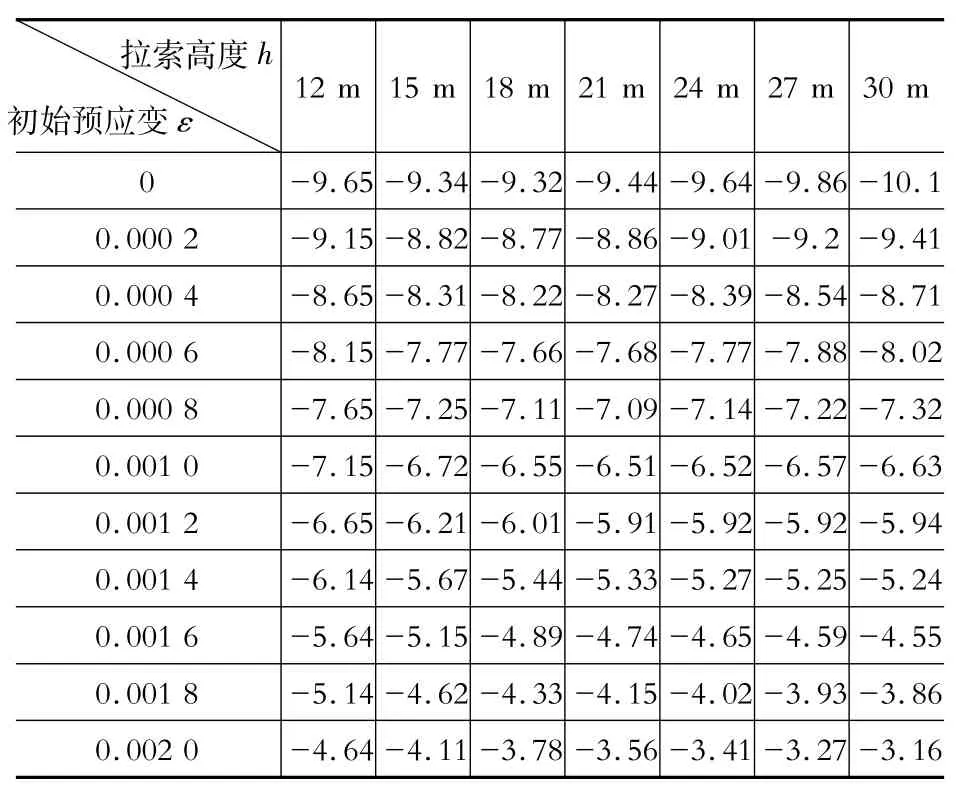
表1 静力作用下自由端位移ΔTable 1 Displacement of the free endΔ under static loadscm

经过分析得到初始预应变ε、斜拉索高度h与自由端位移Δ在静力荷载作用下的近似函数表达式为

Δ＝－（40 h＋2 180）ε＋9.8（9）（1）当初始预应变ε≤0.000 6，斜拉索高度

表2 静力荷载作用下下弦杆杆件内力Table 2 Internal forces in the bottomchord bars under static loads kN

由表2的内力分布规律可得其L-Ss曲线，如图3所示，其中，L为桁架下弦杆各节间中点至支座的距离，Ss为静力作用下下弦杆内力。

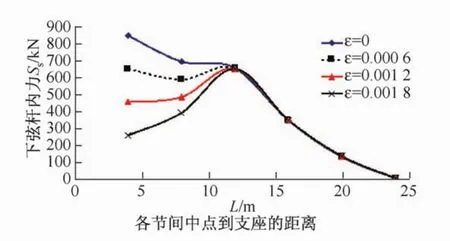
图3 下弦杆内力Ss-L曲线（h＝30 m）Fig.3 Bottom chord bar Ss-L curves（h＝30 m）

分析表2和图3可知：

（1）下弦杆承受压力，考虑稳定分析时要引起重视。

（2）对于一定的斜拉索高度，斜拉索外端的悬臂部分其下弦杆内力不因斜拉索初始预应力的改变而改变，而斜拉索以内的节间其下弦杆内力却随着斜拉索中施加的预应力的不同有着很大的改变（注：图3纵坐标未标出负号，均为压力）。此外，根据预应力施加大小的不同，支座至斜拉索之间的节间其下弦杆内力的变化不如斜拉索以外的节间变化有规律，不同的斜拉索高度有一个“临界预应力值”（此预应力值影响下弦杆的内力：当大于此值时下弦杆内力单调增加；当小于此值时单调减少），如表3所示。

表3 临界预应变值εcrTable 3 Critical prestrain valueεcr

经过分析可知：当斜拉索高度大于21 m时，此临界值几乎保持不变（即初始预应变为0.001）；而当斜拉索高度小于21 m时，此临界值与斜拉索高度有近似抛物线的关系，即：

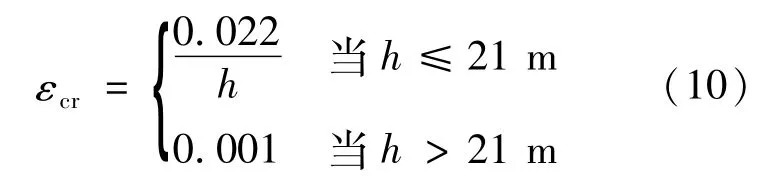
3.3.3 静力作用下斜拉索内力

静力作用斜拉索内力F和斜拉索高度h、初始预应变ε的关系如图4所示。

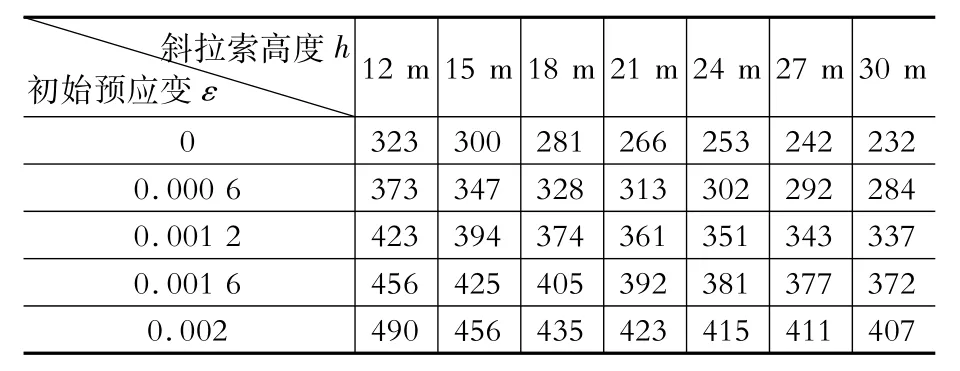
表4 静力荷载作用下斜拉索内力Tab le 4 Cable internal forces under static loads kN

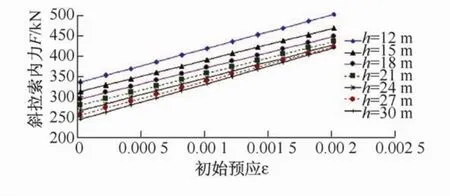
图4 静力作用下斜拉索内力F—初始预应变ε曲线Fig.4 Cable internal force F-initial prestrain εcurves under static loading

由表4、图4分析可知：

（1）对于同一斜拉索高度，斜拉索内力与初始预应变成正比，且不同的斜拉索高度其斜率几乎相同。随着斜拉索高度的增加，其内力逐渐减小，斜拉索内力与初始预应变成正比。

（2）初始预应变越小，斜拉索内力与斜拉索高度的线性关系越强，反之越弱。

4 结 论

本文利用有限元软件ANSYS对斜拉空间桁架结构进行建模，通过对斜拉索施加不同大小的预应力进行对比分析，确定斜拉索高度和初始预应变对该类结构的内力和位移影响，得出内力系数与节间位置、预应力以及斜拉索高度之间的关系曲线。同时，对其在静力作用下的力学性能进行了详细的计算和分析，回归出在静力荷载作用下初始预应变（应力）与自由端位移（或挠度）的函数关系：Δ＝－（40 h＋2 180）ε＋9.8。

本文在以下4个方面还有待于进一步深入研究［8，9］：

（1）斜拉空间结构在风荷载作用下反应（内力及自由端位移与斜拉索施加预应力大小的关系）的研究不应该被忽略。

（2）对于斜拉空间结构，布置多根索（如放射式布索、竖琴式布索、扇形式布索和星式布索等）对于结构静力、动力、风振及稳定的影响程度。

（3）本文未考虑斜拉空间桁架结构出平面稳定，可以进一步研究檩条及水平支撑对于其出平面稳定影响的量化。

（4）本文未考虑立柱变形的影响，全面考虑立柱的变形对本结构内力及位移的影响将具有更加现实的意义。

［1］ 陆赐麟，尹思明，刘锡良.现代预应力钢结构［M］.北京：人民交通出版社，2003.Lu Cilin，Yin Siming，Liu Xiliang.Modern prestressed steel structures［M］.Beijing：China Communications Press，2003.（in Chinese）

［2］ 王新堂.计算结构力学［M］.北京：科学出版社，2001.Wang Xintang.Computational structural mechanics and applications［M］.Beijing：Science Press，2001.（in Chinese）

［3］ 葛家琪，张国军，王树，等.贵阳体育场体外预应力大悬挑钢管桁架结构设计研究［J］.建筑结构学报，2009，28（10）：52-57.Ge Jiaqi，Zhang Guojun，Wangshu，et al.Research and analysis on large span external prestressed cantilever pipe truss of Guiyang sports center［J］.Journal of Building Structures，2009，28（10）：52-57.（in Chinese）

［4］ 孙金国，徐小兵，陈杰，等.大跨度张弦桁架结构静力和自振特性研究［J］.苏州科技学院学报，2012，25（6）：2-5.Sun Jingguo，Xu Xiaobing，Chen Jie，et al.The analysis of static and free vibration characteristic of long-span truss string structure［J］.Journal of Suzhou University of Science and Technology，2012，25（6）：2-5.（in Chinese）

［5］ 石启印，蔡永刚，李爱群，等.大跨度张弦桁架结构自振特性和地震响应分析［J］.四川建筑科学研究，2012，38（3）：154-159.Shi Qiyin，Cai Yonggang，Li Aiqun，et al.Analysis of free vibration characteristics and seismic response of long-span truss string structure［J］.Sichuan Building Science，2012，38（3）：154-159.（in Chinese）

［6］ 爱德华.L.威尔逊.结构静力与动力分析［M］.北京：中国建筑工业出版社，2006.Edward L Wilson.Static and dynamic analysis of structure［M］.Beijing：China Building Industry Press，2006.（in Chinese）

［7］ 刘士林，梁智涛，孟凡超，等.斜拉桥［M］.北京：人民交通出版社，2002.Liu Shilin，Liang Zhitao，Meng Fanchao，et al.Cable stayed bridge［M］.Beijing：China Communications Press，2002.（in Chinese）

［8］ 葛家琪，张国军，王树，等.2008奥运会羽毛球馆弦支穹顶结构整体稳定性能分析研究［J］.建筑结构学报，2007，28（6）：22-30.Ge Jiaqi，Zhang Guojun，Wang Shu，et al.The overall stability analysis of the suspended dome structure system of the badminton gymnasium for 2008 O-lympic Games［J］.Journal of Building Structures，2007，28（6）：22-30.（in Chinese）

［9］ 张国泉，孙东利.矮塔斜拉桥刚度参数的影响行为［J］.结构工程师，2013（1）：27-32.Zhang Guoquan，Sun Dongli.Extra-dosed prestressing concrete bridge influence the behavior of the stiffness parameters［J］.Structural Engineers，2013（1）：27-32.（in Chinese）

Performance Study of a Cable-stayed Spatial Truss under Static Loads

WANG Xin1，*WANG Changlin2YAN Zhenguo
（1.School of Civil Engineering，Huazhong University of Science and Technology Wuchang Branch，Wuhan 430064，China；2.Hubei Huaxing，Architecture Co.Ltd.，Wuhan 4332200，China；3.Hubei Hongye，Architectural Design Co.Ltd.，Wuhan 430056，China）

Internal force and displacement of the free end under the static state of a cable-stayed space truss was calculated by using the finite element analysis software ANSYS.The relations between the internal force coefficient and the inter-node position，height，prestressed cable were summarized.The influence of cable prestress and the cable height on the internal force and displacement at the free end of the structure was analyzed in detail.The concept of critical pre strain in cable-stayed space trusswas raised.The relations between the free end displacement，the initial pre strain，and the cable heightwere derived.

cable-stayed spatial truss，static load，finite elementanalysis，critical prestrain，inner force coefficient

2013－11－09

*联系作者，Email：wxinstar＠163.com