重型车辆与桥梁耦合振动及桥梁冲击系数的数值模拟研究

王 娟 钱 江

（同济大学结构工程与防灾研究所，上海200092）

重型车辆与桥梁耦合振动及桥梁冲击系数的数值模拟研究

王 娟*钱 江

（同济大学结构工程与防灾研究所，上海200092）

为了更合理地评估桥梁在重型车辆作用下的耦合动力响应，在有限元软件LS-DYNA的平台上，根据车桥振动实验数据，建立了具有11个自由度的3轴重型车辆和桥梁上部结构的车桥耦合系统有限元模型。对桥梁模型进行了模态分析，并对车桥耦合振动的三个工况进行了数值模拟，所得结果与实测数据一致，验证了有限元模型的合理性、可靠性。进一步利用该有限元模型进行车桥耦合体系参数分析，选择了车辆运行速度，桥梁桥台搭板的沉降以及桥梁跨度进行桥梁冲击系数的参数敏感性研究。参数分析结果表明：冲击系数整体上随车辆速度的增大而增大，同时有局部极大值的存在；冲击系数随桥台搭板沉降量的增大而增大；冲击系数呈现随桥梁跨度的增大而增大的趋势。

车-桥耦合振动，冲击系数，LS-DYNA，重型车辆

1 引 言

近年来，随着公路货运重型大型车辆的高速发展，车桥耦合振动的相关研究成为研究的热点，尤其交通运输中桥梁损毁事件屡见报端，因而正确评估重型车辆对桥梁的动态性能影响显得尤为重要。桥梁动态响应的确定是根据车辆静力作用乘以冲击系数得出，按照我国《公路桥涵设计通用规范》［1］的规定，冲击系数仅仅考虑了桥梁的自振频率的影响。实际上，桥梁和车辆是相互作用的耦合系统，影响桥梁动态响应的因素基本分为三类：第一类是桥梁的固有特性，比如自振频率、跨长［2］等；第二类为车辆的特性，包括振动频率、阻尼和运行速度等；第三类包括其他影响桥梁响应的因素，比如桥面的不平整度、桥台搭板沉降等。由于桥梁节点处两侧桥面板不均匀沉降或桥台搭板的沉降会造成车辆激励的显著增大，其中针对桥台搭板的沉降对桥梁的影响，美国桥梁规范［3］允许桥梁节点的设计采用0.75作为冲击系数，而我国规范并未做出相应规定。

在理论研究方面，很多学者通过建立简单的车桥模型求解车桥耦合振动方程的解析解或者数值解析解。比如桥梁模拟成简支梁，车辆以单轴质量弹簧系统代表［4，5］。尽管这种简单模型提供了理论参考价值，但由于过于简化无法应用于实际工程。有些学者通过编程解决车桥耦合运动方程，可以解决相对复杂的问题，但由于编程的复杂性使其不易推广。比如侯永姣等［6］采用拟力法处理车辆模型求解车辆耦合振动方程；杨建荣等［7］采用单轴车辆模型研究了车桥耦合系统的迭代解法。随着计算机硬件和软件的快速发展，基于有限元方法的数值模拟软件已被广泛采用。值得一提的是，超强计算机的应用使精细化的车辆和桥梁模型的建立成为可能，提供了精确模拟车桥耦合系统的方法，但同时也增加了计算成本和时间。实验手段因其可靠性并能够验证有限元模型而成为一种重要研究方法，但由于实验代价较高，不可能进行详尽的参数研究。

基于上述原因，本文对车桥耦合振动系统以有限元软件LS-DYNA为平台建立了11个自由度的3轴重型车辆和桥梁上部结构模型。车桥耦合模型规避了模型的复杂性并兼顾了计算的可靠性和计算效率。通过与实验数据对比验证了有限元模型的合理性、可靠性。选择了车辆运行速度，桥台搭板沉降量和桥面不平整度为参数，研究了桥梁冲击系数的敏感性。

2 车桥耦合振动方程

基于有限元方法的车桥耦合振动基本方程可以表示成矩阵形式［8］，桥梁的控制方程为［Mb］｛d··

b｝＋［Cb］｛d·b｝＋［Kb］｛db｝＝｛Fb｝（1）式中，［Mb］，［Cb］，［Kb］分别为桥梁的质量、阻尼和刚度矩阵；｛db｝为桥梁节点位移向量；｛Fb｝为作用在桥梁上的轮胎与桥梁的接触力向量。

车辆的控制方程为

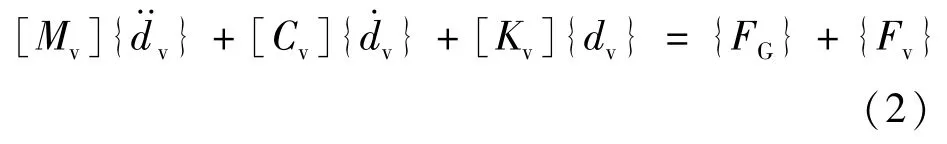
式中，［Mv］，［Cv］，［Kv］分别为车辆的质量、阻尼和刚度矩阵；｛dv｝为车辆节点位移向量；｛FG｝为车辆节点重力向量；｛Fv｝为作用在轮胎上的车辆与桥梁之间的接触力向量。

利用位移连续条件和接触力的关系，方程式（1）、式（2）可以写成：

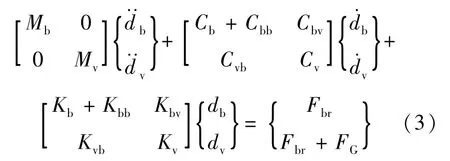
式中，Cbb，Cvb，Cbv，Kbb，Kbv，Kvb，Fbr是由于车桥接触造成的增加项。

方程式（3）中的各项随车辆的运行而变化，因而属于时变系统。

3 车桥耦合系统有限元模型

重型车辆和桥梁模型根据文献［9-11］的实验数据建立。文献中的实验是以重型车辆的运行作为激励测量桥梁动力特性和动态响应的实验。车辆和桥梁的耦合振动通过有限元软件LS-DYNA中的关键字RAIL［12］实现，其中，RAIL＿TRAIN关键字定义了轮胎与轨道接触的部分，接触算法是通过罚函数实现。RAIL＿TRACK定义了车辆运行的轨道，轨道由一系列梁单元组成嵌入桥梁单元，采用空材料（Null Material）以避免增加系统刚度。RAIL关键字同时允许施加路面的不平整度和轮胎的粗糙度。这种算法由英国Arup公司开发，为研究包括行人车辆等移动荷载造成建筑结构动态响应提供了方便。

3.1 车辆模型

场地实验中采用的车辆是可以简化成三轴的五轴重型卡车（图1（a）），总重量为319 kN（32.5 t），其中前轴重量50 kN，中轴重量100 kN，后轴重量169 kN。车辆模型根据美国规范［3］中车辆荷载HS 20-44建立。这种简化车辆模型兼顾了计算效率的同时体现了重型车辆多轴动力特性。如图1（b）所示，车辆由拖车、挂车、悬挂系统和轮胎组成，其中拖车和挂车用球型铰连接，并用刚体材料模拟，轮胎用单点质量单元模拟，悬挂系统和轮胎的刚度用弹簧阻尼系统模拟。考虑到拖车和挂车之间的连接关系并对车辆模型施加约束，使其具有11个自由度，包括6个轮胎竖直方向的位移y11，y21，y31，y12，y22，y32，拖车和挂车竖直方向的位移y1和y2，拖车和挂车的仰俯转角θ1和θ2，车体倾覆转角θ3。车辆的参数如表1所示，悬挂系统和轮胎的刚度满足车辆的三个轴重，几何尺寸及其他参数参考文献［11］并做部分调整。通过模态分析得出车辆模型的整体竖向弹跳模态对应的频率为3.42 Hz。

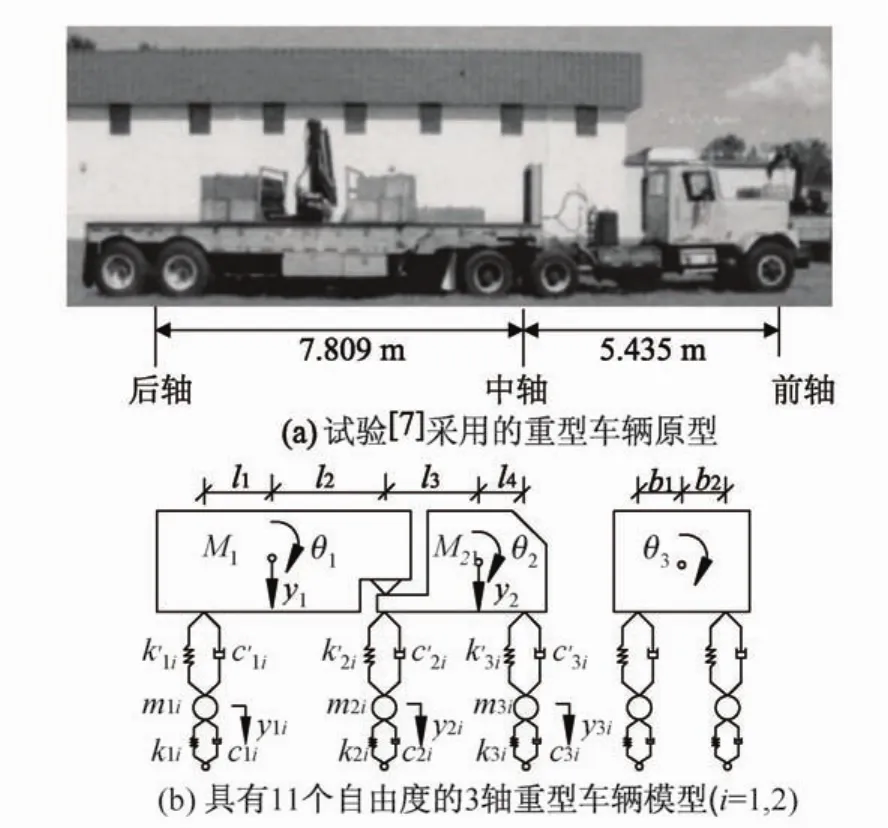
图1 重型车辆模型Fig.1 Analyticalmodel of a heavy truck

表1 卡车模型参数Table 1 Parameters of the truck model

3.2 桥梁模型

实验中的桥梁位于美国佛罗里达州，由护栏、板和大梁构成的混凝土跨线桥［11］。整个桥梁有三跨，每跨长度21.7 m，宽度14.15 m。桥面板厚度0.2 m，由6根间距2.4 m的I字形大梁支撑（图2）。由于桥梁每跨单独制作，并非连续性桥梁，因而只建立与公路相连的第一跨桥梁的上部结构模型。

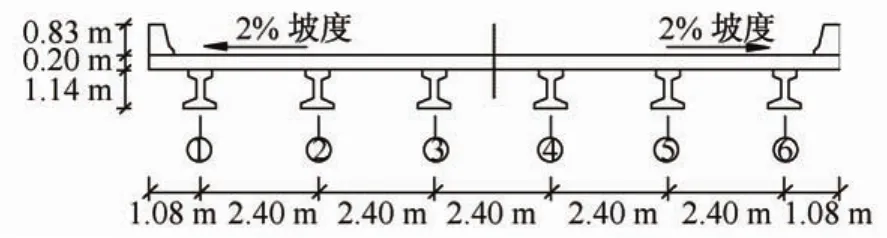
图2 桥梁上部结构横截面Fig.2 Cross section of a bridge

图3 桥梁的有限元计算模型Fig.3 Analytical finite elementmodel of the bridge

为了规避三维实体模型的计算代价，并确保数值模拟的可靠性，桥梁的护栏，板和大梁均采用分层壳单元进行模拟。分层壳单元的截面简化计算方法参考文献［13］，护栏和大梁截面简化过程遵循的原则是面积守恒和惯性矩守恒，并保持截面高度不变。分层壳单元的设置通过LS-DYNA软件中的关键字PART＿COMPOSITE实现，这个关键字允许对壳单元中的每一层分别设置不同材料参数，比如弹性模量和密度等。计算模型如图3所示，沿桥梁横向壳单元采用三种截面类型，分别代表护栏、板和大梁，其中大梁和板的单元类型交替布置。板对应的壳单元分成均匀6层，其中包含两层钢筋层，护栏位置的壳单元分成20层，其中包含位于下部的6层板单元，大梁位置的壳单元分成26层，其中包含位于上部的6层板单元。不同壳单元的每一层按照对应构件（大梁、护栏和板）的不同分别定义材料参数。由于实验观测到的动态变形较小，材料类型采用线弹性材料，材料常数按照混凝土核心试验测得的数据采用［10］。

正确模拟桥梁模型的关键因素是橡胶支座模型的建立。本文采用LS-DYNA软件中的离散梁单元（discrete beam element）模拟支座。这种单元类型可以方便的定义三个坐标轴方向的拉伸刚度和旋转刚度，刚度参数的选择参照文献［14］。桥梁模型的边界约束条件施加在支座上，并且没有考虑支座与大梁和墩台的摩擦和接触。

3.3 有限元模型的验证

桥梁模态分析是模型验证的重要步骤。从模态分析结果中识别出三种模态和频率与实验结果接近，如图4所示。由表2可以看出数值模拟结果与实验结果吻合良好，第一阶频率的误差为2.17%，表明了桥梁模型的可靠性。

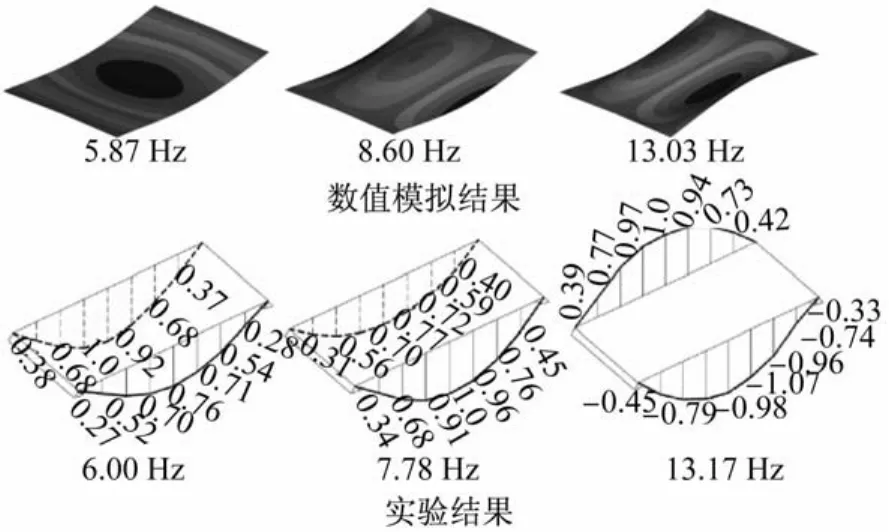
图4 桥梁模态和频率的有限元结果和实验结果［11］的对比Fig.4 Comparison of vibration modes between FE and experimental data

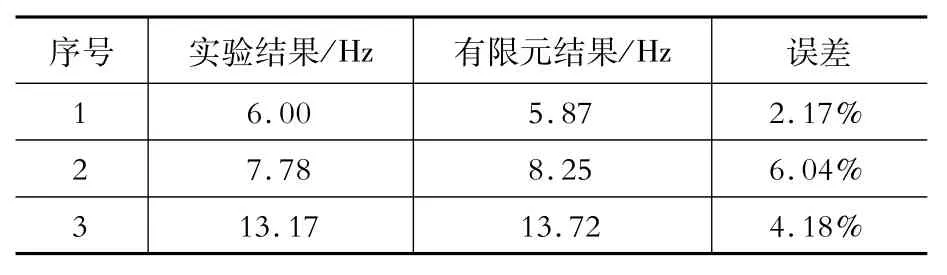
表2 有限元结果和实验结果的频率对比Table 2Comparison of natural frequency between finite element and testing results

与实验动态时程结果的对此可以验证车桥耦合模型的可靠性。本文选取了三个实验工况进行模拟，第一个工况是车辆以48 km／h的速度运行在桥梁横向的中间位置上；第二个工况是车辆以80 km／h的速度运行在桥梁横向的中间位置上，并且在桥梁跨中横向布置了截面为40 mm厚、400 mm宽的木板（木板的设置是为了增加车辆的激励作用并模拟恶劣的路面粗糙度［9］）；第三个工况是车辆以48 km／h的速度运行在桥梁横向的远离测量点的对面车道位置上。位移时程测量点在3号大梁的跨中位置（图2），加速度时程的测量点在跨中护栏内侧的桥面板上。

数值模拟的结果没有进行滤波处理。第一个工况的模拟结果与实验结果的对比如图5和图6所示。从图5可以看出位移时程的曲线趋势与实验结果接近，实验结果的最大位移为2.22 mm，数值模拟结果为2.26 mm，从图6的加速度时程可以看出，尽管两种结果的频率不一致，但曲线的幅值和整体的趋势吻合良好。图7和图8分别为第二个和第三个工况的位移时程结果对比，这两个结果对比均显示了良好的吻合性，从而验证了车桥耦合模型的准确性。

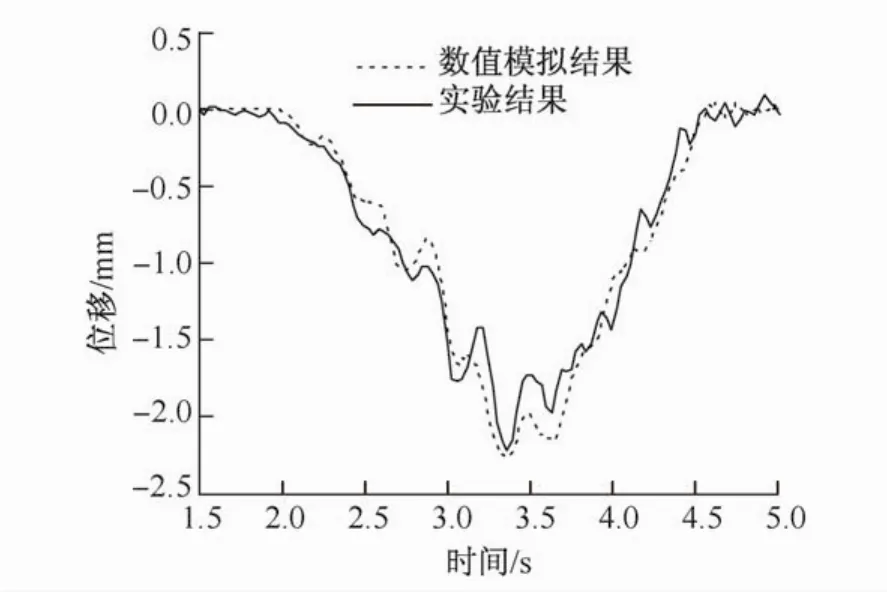
图5 在48 km／h速度下竖向动态位移的有限元结果和实验结果的对比Fig.5 Vertical dynamic displacement comparison between experimental data and FE results at velocity of 48 km／h

图6 在48 km／h速度下加速度的有限元结果和实验结果的对比Fig.6 Acceleration comparison between experimental data and FE results at velocity of48 km／h

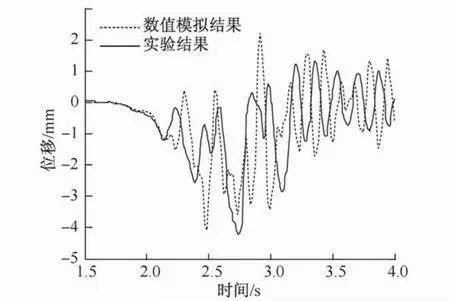
图7 在80 km／h速度下桥梁竖向动态位移的有限元结果和实验结果的对比Fig.7 Vertical dynamic displacement comparison between experimental data and FE results at velocity of80 km／h

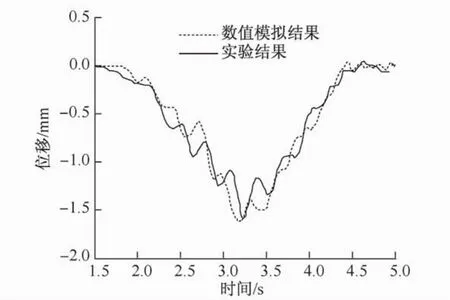
图8 运行在对面车道的车辆在48 km／h速度下桥梁竖向动态位移的有限元结果和实验结果的对比Fig.8 Vertical dynamic displacement comparison between experimental data and FE results at velocity of 48 km／h with truck on the other lane

4 桥梁在车辆作用下的动态响应

冲击系数是评估桥梁承受车辆作用的指标，公式如下：

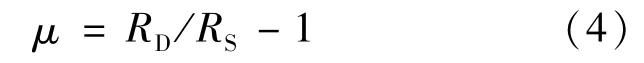
式中，μ为冲击系数；RD为桥梁在车辆作用下的最大动态响应；RS为桥梁在车辆作用下的最大静态响应。

可以选择位移、弯矩和应变作为响应进行计算，本文采用竖向位移响应计算冲击系数。

车辆速度是影响桥梁响应的重要参数，本文按增量5 km／h选取车辆速度从30 km／h到120 km／h计算冲击系数，如图9所示。从图9曲线可以看出冲击系数的整体趋势随速度的增加而增加，同时存在一些局部极值，说明冲击系数不是随速度单调增加。这种由速度引起的局部极值点的现象发生在单质量、单轴及双周车辆模型的车桥耦振动中，已在Fryba［5］的书中有所论述。但对三轴车辆模型引起的局部极值点的现象并未见其他文献报道。

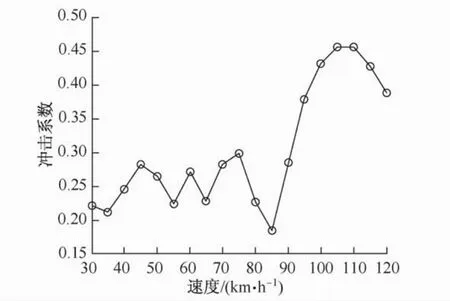
图9 不同速度下的冲击系数Fig.9 Impact factors at various velocities

由于桥梁使用时间的增加会导致桥台搭板的沉降，或者桥梁节点处两边桥面的不均匀沉降造，从而造成成桥面凹陷，导致车辆的激励增大，并增加了桥梁或节点处的动态响应。

参照文献［15］中的桥台搭板沉降计算模型（图10），由于Δ2，Δ3的变化对桥梁的动态响应的影响比Δ1小［15］，本文设定Δ2＝0，Δ3＝0，只考虑Δ1的变化。本文选择了沉降量Δ1＝5mm，10mm，20 mm，30 mm，并在车辆速度为60 km／h的条件下进行计算。如图11所示，不同的沉降量对应的桥梁跨中节点处的位移时程表明：随Δ1的增加，最大位移显著增大。不同沉降量对应的最大位移分别为－2.23 mm，－2.36 mm，－2.72 mm和－2.89 mm，相应的冲击系数分别为0.21，0.28，0.48和0.57。车辆第一个轴的轴力时程如图12所示，表明沉降量的增大导致车辆轴力的增大，从而造成冲击系数的增大。

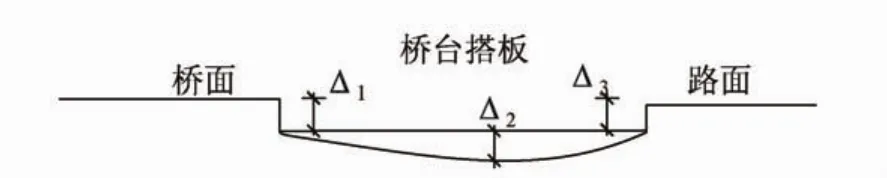
图10 桥台搭板沉降计算模型［15］Fig.10 Model of approach slab deformation［15］

文献［15］表明短跨桥梁对沉降量的变化比较敏感，为了考察沉降量对不同跨度的桥梁影响，通过改变现有桥梁模型的跨度［11，16］和大梁的截面高度［16］，分别建立了跨度为16 m，26 m，30 m和34 m的桥梁模型。包括跨度为21.7 m的实验桥梁模型的5个跨度的桥梁对应的第一个竖向振动模态的频率分别为8.60 Hz，5.87 Hz，4.81 Hz，3.40 Hz，2.88 Hz，车辆的整体竖向振动频率为3.42 Hz，设r为车辆频率和桥梁频率的比，则r＝0.4，0.58，0.71，1.01和1.18。

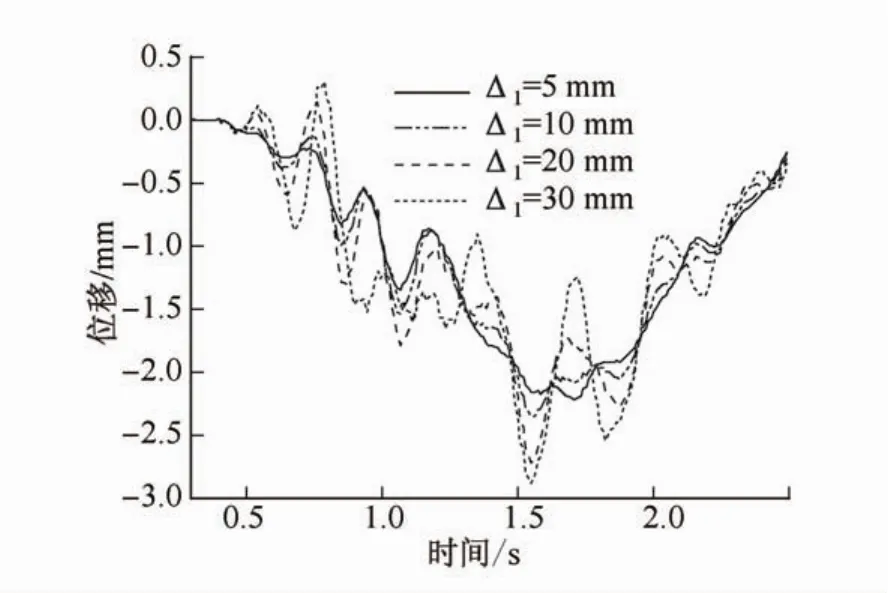
图11 在60 km／h速度下不同桥台搭板沉降量的桥梁跨中竖向动态位移Fig.11 Dynamic vertical displacements atmidpoint of bridge at various approach slab settlements under 60 km／h traveling speed

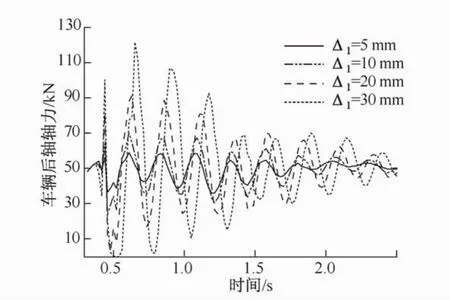
图12 在60 km／h速度下不同桥台搭板沉降量的车辆第一轴的轴力时程Fig.12 Time histories of the first axle forces at various approach slab settlements under 60 km／h traveling speed

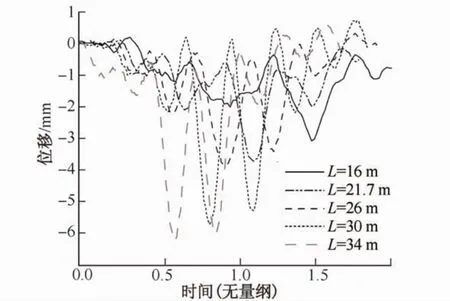
图13 在120 km／h速度下，桥台搭板沉降量为20 mm时不同跨度桥梁的跨中动态位移Fig.13 Dynamic vertical displacements atmidpoint of bridge for various span lengths with 20 mm approach slab settlement under 120 km／h traveling speed

为了便于比较，本文采用了无量纲时间参数，即

式中，τ为无量纲时间参数；t为车辆运行时间；L为桥梁的跨长；v为车辆运行速度。

在车辆运行速度为120 km／h的作用下，不同跨度桥梁在沉降量Δ1＝20 mm的跨中位移时程如图13所示，不同的沉降量对应的冲击系数如表3所示。图13中曲线表明，随着桥梁跨度的增大，即桥梁自振频率的减小，桥梁的动态位移随之增大。从表3可以明显看出，相同的Δ1值对应的冲击系数在r＝1.01时最大，此时桥梁和车辆耦合共振。除去共振的因素，相同的Δ1值对应的冲击系数基本随频率的减小而增大，表明桥梁柔度的增加会导致动态响应的增加。我国桥梁规范［1］中规定跨度5 m≤L＜20 m属于小桥，20 m＜L≤40 m属于中桥，本文的算例中16 m的桥梁对应的冲击系数没有呈现出对沉降量敏感的趋势。

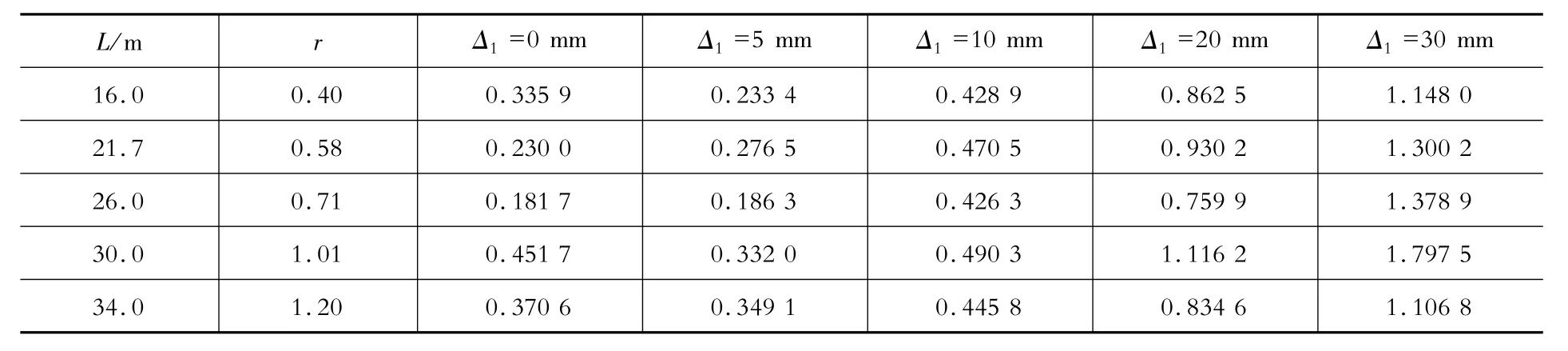
表3 桥台搭板沉降量对不同跨度桥梁的冲击系数的影响Table 3 The effect of settlem ent of app roach slab on im pact factor of bridge of various span length

5 结 语

本文基于车桥耦合振动的场地实验在LSDYNA的平台上建立了车辆和桥梁的有限元模型，通过与实验的模态频率和时程数据的比较，验证了有限元模型的合理性、可靠性，并对车辆运行速度、桥台搭板沉降量和车桥频率比对冲击系数的影响进行了研究。

参数研究结果表明，车辆运行速度的增加整体上会导致桥梁冲击系数的增大，同时在某些速度下冲击系数存在局部极大值，表明桥梁的冲击系数并非随速度单调增加；桥台搭板沉降量对桥梁的冲击系数影响较大，是由于桥台搭板的增加导致车辆轴力的增加造成；相同沉降量的条件下，冲击系数呈现随桥梁跨度增加而增大的趋势，在车桥频率比为1附近的共振点冲击系数显著增加。

［1］ 中华人民共和国交通部.JTG D60—2004公路桥涵设计通用规范［S］.北京：人民交通出版社，2004.Ministry of communications of the people′s Republic of China.JTG D60—2004 General code for design of highway bridges and culverts［S］.Beijing：China Communications Press，2004.（in Chinese）

［2］ 吕佳，吴定俊，李奇.简支梁桥位移与内力动力系数差异研究［J］.结构工程师，2012，28（4）：78-83.Lu Jia，Wu Dingjun，Li Qi.Study on difference between displacement and internal force dynamic impact factor of simply-supported bridges［J］.Structural Engineers，2012，28（4）：78-83.（in Chinese）

［3］ American Association of State Highway and Transportation Officials.LRFD bridge design specification［S］.Washington，D.C.，2004.

［4］ Olsson M.Finite element，modal co-ordinate analysis of structures subjected to moving loads［J］.Journal of Sound and Vibration，1985，99（1）：1-12.

［5］ Fryba L.Vibration of Solids and Structures under Moving Loads［M］.3rd Edition.Thomas Telford，London，1999.

［6］ 侯永姣，吴定奇，李奇.车桥耦合振动分析中基于虚拟力的车辆建模方法［J］.结构工程师，2012，28（3）：55-59.Hou Yongjiao，Wu Dingjun，LiQi.Dynamic analysis method for vehicles based on force analogymethod in coupled vehicle-bridge systems［J］.Structural Engineers，2012，28（3）：55-59.（in Chinese）

［7］ 杨建荣，刘章军.车-桥耦合系统迭代解法研究［J］.结构工程师，2007，23（4）：41-44.Yang Jianrong，Lu Zhangjun.Iterative procedure for dynamic analysis of vehicle-bridge interaction［J］.Structural Engineers，2007，23（4）：41-44.（in Chinese）

［8］ Deng L，Cai C S.Development of dynamic impact factor for performance evaluation of existing multigirder concrete bridges［J］.Engineering Structures，2010，32：21-31.

［9］ Kwasniewski L，Wekezer J，Roufa G，et al.Experimental evaluation of dynamic effects for a selected highway bridge［J］.Journal of Performance of Constructed Facilities，2006，20（3）：253-260.

［10］ Kwasniewski L，Li H，Wekezer J，et al.Finite-element analysis of vehicle-bridge interaction［J］.Finite Elements in Analysis and Design，2006，42（11）：950-959.

［11］ Li H，Wekezer J，Kwasniewski L.Dynamic response of highway bridge subjected tomoving vehicles［J］.Journal of Bridge Engineering，2008，13（5）：439-448.

［12］ Hallquist JO.LS-DYNA Keyword User′s Manual，Livermore software technology corporation，Livermore，California，2013.

［13］ Kwasniewski L.Nonlinear dynamic simulations of progressive collapse for amultistory building［J］.Engineering Structures.2010，32：1223-1235.

［14］ Cook R A，Allen D T，Ansley M H，et al.Stiffness evaluation of neoprene bearing pads under long term loads［R］.University of Florida，2009，55-74.

［15］ Shi X，Cai C S，Chen S，et al.Vehicle induced dynamic behavior of short-span slab bridges considering effect of approach slab condition［J］.Journal of Bridge Engineering，2008，13（1）：83-92.

［16］ Liu C，Huang D，Wang Ton-Lo，et al.Analytical dynamic study based on correlated road roughness［J］.Computers and Structures，2002，80：1639-1650.

Numerical Simulation of Bridge-and-heavy-vehicle Coupling Vibration for the Im pact Factor Study

WANG Juan*QIAN Jiang
（Research Institute of Structural Engineering and Disaster Reduction，Tongji University，Shanghai200092，China）

In order to efficiently evaluate the dynamic response of bridge under passage of vehicles，the superstructure of a bridge coupled with an heavy vehiclemodel of11 degrees of freedom with three axleswas developed by using LS-DYNA software based on available field tests.To validate reliability and efficiency of the finite element（FE）models and the corresponding algorithm，analyseswere carried out and three testing cases were selected for comparison.Good correlation between FE and experimental results confirms that the FEmodel is reliable for parametric studies.Three parameters includingmoving velocity of vehicle，the settlement of approach slab and the span length of the bridge，which has influence on the impact factor，were investigated.Numerical results show that impact factor increaseswith velocity whilemay reach its localmaximum somehow.It goes up with the increase of approach slab settlement.It has a tendency to increase with the increase of bridge span length.

dynamic response，LS-DYNA，finite elementmodel，impact factor，parameter study

2013－08－07

科技部国家重点实验室基金项目（SLDRCE10-B-07）*联系作者，Email：09 jwang＠tongji.edu.cn