全空间瞬变电磁法资料解释方法中的平移算法

杨海燕，邓居智，汤洪志，林 云

东华理工大学放射性地质与勘探技术国防重点学科实验室，南昌 330013

0 引言

在地面瞬变电磁法晚期视电阻率公式研究与应用成熟以后，全区视电阻率计算方法逐渐成为研究热点。在此过程中产生的计算方法主要有连分式定义法、逆样条插值计算法、平移算法及二分搜索算法等［1－9］，它们研究的出发点与研究重点主要为：1）探求早期和晚期视电阻率的精确解法［1－2］；2）避免因感应电位核函数非线性产生的早晚期响应混淆，获取同一感应电位对应的早期响应或晚期响应的唯一解［4，6，9］；3）实现过渡区视电阻率的精确计算［5，8］。

视电阻率的精确计算在地下瞬变电磁法数据处理与解释中仍具有重要意义，其理论研究虽较地面瞬变电磁法落后，但已有发展。现有的研究成果显示，全空间晚期视电阻率为半空间晚期视电阻率的某一特定倍数［10－13］。而地下瞬变电磁法全区视电阻率的研究却颇显滞后，成果也较为少见。地下瞬变电磁法全区视电阻率定义类似于地面瞬变电磁法，且其计算方法已有过讨论［10］，多数半空间全区视电阻率计算方法仍适用于全空间。文献［8］提出的地面瞬变电磁法平移算法速度快、精度高、算法稳定，无需迭代和求解非线性方程，且具有唯一解；同时，全空间瞬变响应曲线也具有平移伸缩特性，因而该方法可适用于地下瞬变电磁法的研究［10］。基于该方法的上述优点和地下瞬变电磁法全区视电阻率的研究现状，探讨其在地下瞬变电磁法应用中的有效性和精确性显得极为必要。

1 理论基础

1.1 视电阻率常规算法

由水平圆形回线源感应电动势定义的视电阻率计算公式［10，14］，晚期视电阻率为

全区视电阻率为

其中，X为下述方程的解：

1.2 视电阻率平移算法

因全空间瞬变响应曲线也具有平移伸缩特性［10］，故可将半空间视电阻率平移算法引入至全空间计算中，定义参数如下［8］。

由理论值计算的平移截距为

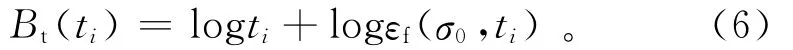
式中，ti为电导率为σ0的均匀全空间介质的理论响应时刻。

由观测值计算的平移截距为

式中，tj为实测电流归一化感应电动势（V/I）j对应的采样延时。

则时间道tj对应的视电阻率计算公式为

2 核函数曲线与截距曲线

为分析平移截距与核函数的对应关系，并研究平移算法的实质，现将式（5）右端项中的时间参数t移至左端后取对数，得

式（10）中的等号左端项正是理论平移截距，而右端

项则为核函数对数的常数倍（装置参数及电流不变），由此可知，全空间理论平移截距曲线与其对应的核函数曲线随时间t具有相似的变化趋势。对半空间理论平移截距与核函数也可得出相同结论。因而平移算法的实质是寻找对应参数下的理论核函数，使其与由观测值计算的核函数达到最佳拟合。这一过程通过平移截距实现，其理论基础与常规的全区视电阻率理论（式（3）－（5））一致。

图1为半空间与全空间核函数和平移截距曲线图，计算中除电导率变化外其余参数均相同。在同一电导率参数下，核函数曲线与平移截距曲线之间对应关系如前分析（无论半空间还是全空间均如此），2支曲线的极大值点对应时刻亦相同。以极值点为界将平移截距曲线分成左右2支，左支曲线对应瞬变早期，右支曲线对应瞬变晚期，极值点附近对应过渡区。当介质电导率变化时，核函数曲线和平移截距曲线均作相同方向的平行移动，表现了该算法的平移伸缩特性。

3 算例与实例

3.1 理论数据计算

图2为电阻率为10Ω·m的均匀半空间和全空间视电阻率曲线，计算中分别采用常规算法和平移算法。常规算法包括视电阻率早期公式和晚期公式，而平移算法则包括早期公式（仅采用左支截距计算）、晚期公式（仅采用右支截距计算）及全区公式，以此来分析平移算法早、晚期及全区公式的精确性。由图2可以看出：由平移算法计算的早、晚期视电阻率曲线与由常规公式计算的曲线具有相似的衰减特征，但在过渡区附近平移算法的精度更高；而平移算法全区视电阻率曲线在整个采样时间段内都能较好地反映出模型电阻率，因而效果更佳。由此验证了平移算法的精确性及其在全空间视电阻率计算中的适用性。

3.2 模拟数据计算

图3为由数值模拟结果计算的视电阻率曲线。选用五层地质结构模型，巷道位于第二层介质内。数值模拟方法为时间域有限差分法，巷道内场量计算采用Laplace方程，截断边界条件为修正的廖氏吸收边界条件［15－17］。从图中可以看出，2种方法计算的视电阻率曲线吻合较好，且反映出了模型各层的电性特征。

3.3 实测数据计算

为深入分析平移算法在全空间资料处理与解释中的应用效果，进而探索更有效的资料解释手段，采用平移算法对某煤矿井下实测资料进行处理与分析。图4为由截距参数绘制的时间剖面图和由视电阻率绘制的视电阻率断面图（深度计算公式采用文献［18］所研究公式）。断面图中显示出在A、B两测点附近各存在一个异常区，其深度范围均在20～80 m内。此外，横坐标为180m处类似于一个弱异常区，深部（大于80m）视电阻率曲线连续性较好。时间剖面图中的A、B位置也分别显示出了异常区的存在，但横坐标为180m处的弱异常区则可以排除。图5为图4中A、B点处的视电阻率曲线，计算中均采用了平移算法（式（9））和晚期视电阻率公式（式（2））。从图5中可以看出，由2种方法计算的视电阻率曲线总体吻合良好。由此可以发现，采用视电阻率断面图和截距时间剖面图进行联合资料解释，更易排除假异常；该算例既给出了全空间视电阻率的又一种计算方法，也探索了另一种联合解释方法。

图1 半空间（a）与全空间（b）核函数曲线和平移截距曲线Fig.1 Kernel function curves and Translation intercept curves for half space（a）and full space（b）

图2 均匀半空间（a）和均匀全空间（b）模型视电阻率计算Fig.2 Apparent resistivity calculation of theoretical value from homogenous half-space（a）and full-space（b）model

图3 五层模型视电阻率计算Fig.3 Apparent resistivity calculation of five-layers model

4 结语

近年来地下瞬变电磁法勘探技术得以不断发展，其资料处理与解释手段也需要进行探索与补充。全空间瞬变电磁响应曲线也具有平移伸缩特性，是半空间平移算法能够应用于全空间的前提条件。全空间平移算法的实质是寻找对应参数下的理论核函数，使其与由观测值计算的核函数达到最佳拟合。其理论基础与常规的全区视电阻率计算一致，但避免了常规解法的多解性问题，因而要优于常规的视电阻率解法。此外，在应用平移算法进行视电阻率计算的基础上，采用截距参数的时间剖面图与视电阻率断面图联合解释产生了较好的应用效果，因而对其进行更深入研究将具有重要意义。

图4 视电阻率断面（a）和截距参数Bo的时间剖面（b）Fig.4 Apparent resistivity section diagram（a）and time cross section of intercept parameter Bo（b）

图5 实测资料视电阻率计算Fig.5 Apparent resistivity calculation of measured data

（

）：

［1］Das U C.Apparent Resistivity Curves in Controlled-Source Electromagnetic Sounding Directly Reflecting True Resistivities in a Layered Earth［J］.Geophysics，1995，60（1）：53-60.

［2］Das U C.Frequency and Time-Domain Electromagnetic Responses of Layered Earth：A Multiseparation， Multisystem Approach ［J］.Geophysics，1995，60（1）：285-290.

［3］朱苏刘，胡文宝.中心回线方式瞬变电磁测深虚拟全区视电阻率和一维反演方法［J］.石油物探，2002，41（2）：216-221.

Zhu Suliu，Hu Wenbao.Pseudo-Full-Region Apparent Resistivity and Its One-Dimensional Inversion for Center-Loop-Line Configuration TEM Data ［J］.Geophsical Prospecting for Petroleum，2002，41（2）：216-221.

［4］翁爱华，陆冬华，刘国兴.利用连分式定义瞬变电磁法全区视电阻率研究［J］.煤田地质与勘探，2003，31（3）：56-59.

Weng Aihua，Lu Donghua，Liu Guoxing.Definition of Whole Zone Apparent Resistivity for Transient Electromagnetic Method of Current Dipole Source［J］.Coal Geology and Exploration，2003，31（3）：56-59.

［5］白登海，Maxwell A Meju，卢健，等.时间域瞬变电磁法中心方式全程视电阻率的数值计算［J］.地球物理学报，2003，46（5）：697-704.

Bai Denghai， Maxwell A Meju，Lu Jian，et al.Numerical Calculation of All-Time Apparent Resistivity for the Central Loop Transient Electromagnetic Method ［J］. Chinese Journal of Geophysics，2003，46（5）：697-704.

［6］熊彬.大回线瞬变电磁法全区视电阻率的逆样条插值计算［J］.吉林大学学报：地球科学版，2005，35（4）：515-519.

Xiong Bin.Inverse Spline Interpolation for the Calculation of All-Time Resistivity for the Large-Loop Transient Electromagnetic Method［J］.Journal of Jilin University：Earth Science Edition，2005，35（4）：515-519.

［7］李建平，李桐林，赵雪峰，等.层状介质任意形状回线源瞬变电磁全区视电阻率的研究［J］.地球物理学进展，2007，22（6）：1777-1780.

Li Jianping，Li Tonglin，Zhao Xuefeng，et al.Study on the TEM All-Time Apparent Resistivity of Arbitrary Shape Loop Source over the Layered Medium［J］.Progress in Geophysics，2007，22（6）：1777-1780.

［8］王华军.时间域瞬变电磁法全区视电阻率的平移算法［J］.地球物理学报，2008，51（6）：1936-1942.

Wang Huajun.Time Domain Transient Electromagnetism All Time Apparent Resistivity Translation Algorithm ［J］. Chinese Journal of Geophysics，2008，51（6）：1936-1942.

［9］陈清礼.瞬变电磁法全区视电阻率的二分搜索算法［J］.石油天然气学报，2009，31（2）：45-49.

Chen Qingli.Searching Algorithm for Full Time Apparent Resistivity from TEM Electromotive Force Data［J］.Journal of Oil and Gas Technology，2009，31（2）：45-49.

［10］杨海燕，邓居智，张华，等.矿井瞬变电磁法全空间视电阻率解释方法研究［J］.地球物理学报，2010，53（3）：651-656.

Yang Haiyan，Deng Juzhi，Zhang Hua，et al.Research on Full-Space Apparent Resistivity Interpretation Technique in Mine Transient Electromagnetic Method［J］.Chinese Journal of Geophysics，2010，53（3）：651-656.

［11］Yu Jingcun，Liu Zhixin，Tang Jinyun.Research on Full Space Transient Electromagnetism Technique for Detecting Aqueous Structures in Coal Mines［J］.Journal of China University of Mining ＆Technology，2007，17（1）：58-62.

［12］杨海燕，岳建华.巷道影响下三维全空间瞬变电磁法响应特征［J］.吉林大学学报：地球科学版，2008，38（1）：129-134.

Yang Haiyan， Yue Jianhua. Response of Characteristics of the 3DWhole-Space TEM Disturbed by Roadway ［J］.Journal of Jilin University：Earth Science Edition，2008，38（1）：129-134.

［13］岳建华，杨海燕，邓居智.层状介质中地下瞬变电磁场全空间效应［J］.地球物理学进展，2012，27（4）：1385-1392.

Yue Jianhua，Yang Haiyan，Deng Juzhi.Whole-Space Effect on Underground Transient Electromagnetic Field in Layered Media［J］.Progress in Geophysics，2012，27（4）：1385-1392.

［14］Kaufman A A，Eaton P A.The Theory of Inductive Prospecting［M］.Amsterdam：Elsevier，2001.

［15］岳建华，杨海燕.矿井瞬变电磁法三维时域有限差分数值模拟［J］.地球物理学进展，2007，22（6）：1904-1909.

Yue Jianhua，Yang Haiyan.3DFinite Difference Time Domain Numerical Simulation for In-Mine TEM［J］.Progress in Geophysics，2007，22（6）：1904-1909.

［16］杨海燕，岳建华.吸收边界条件在全空间瞬变电磁计算中的应用［J］.中国矿业大学学报，2009，38（2）：263-268.

Yang Haiyan， Yue Jianhua. Application of Absorbing Boundary Condition in Whole-Space Computation of Transient Electromagnetic Response［J］.Journal of China University of Mining ＆Technology，2009，38（2）：263-268.

［17］Oristaglio M L.Diffusion of Electromagnetic Fields into the Earth from a Line Source of Current［J］.Geophysics，1982，47（11）：1585-1592.

［18］Yu Jingcun，Wang Yangzhou，Liu Jian，et al.Time-Depth Conversion of Transient Electromagnetic Method Used in Coal Mines［J］.Journal of China University of Mining ＆ Technology，2008，18（4）：546-550.