模式自适应小波时能密度法及其在微差爆破振动信号分析中的应用

张 胜,凌同华,刘浩然,曹 峰

(1．长沙理工大学土木与建筑学院,湖南长沙 410114;2．长沙理工大学桥梁工程安全控制省部共建教育部重点实验室,湖南长沙 410114)

模式自适应小波时能密度法及其在微差爆破振动信号分析中的应用

张 胜1,2,凌同华1,刘浩然1,曹 峰1

(1．长沙理工大学土木与建筑学院,湖南长沙 410114;2．长沙理工大学桥梁工程安全控制省部共建教育部重点实验室,湖南长沙 410114)

如何解决适合爆破振动信号特征的爆破振动信号小波基构造、添加及其实现等问题,始终是困扰广大研究者的难题。为准确确定微差爆破振动信号实际微差延迟时间,在模式自适应小波原理的基础上,构造了从实测微差爆破振动信号中分离出子信号的模式自适应小波基,然后将该模式自适应小波基添加到Matlab小波分析工具箱中,并提出了一种新的基于爆破振动信号分析的模式自适应小波时能密度法。以实验设计的多段微差爆破振动信号进行模式自适应小波时能密度法分析为例,验证了该方法的可行性。该方法亦可用于分析实测微差爆破振动信号在实际微差延迟时间的确定,并与db8小波法和模式自适应小波法进行比较,结果表明模式自适应小波时能密度法具有更好的应用效果,从而为爆破振动信号分析在实际工程中的应用提供了参考。

爆破振动;微差时间;模式自适应小波时能密度法;小波基构造;小波基添加

微差爆破实践中,普通雷管起爆都有延期问题,即便是所谓的高精度雷管,也有±10 ms的误差,由于延期雷管不能准确按设计延期时间起爆,导致微差爆破起爆顺序混乱,影响了实际微差爆破效果与安全[1-2]。因此,研究与确定微差爆破振动信号实际微差延期时间对改进爆破方式、优化爆破参数和控制爆破效果具有重要的指导意义。

从微差爆破振动信号实测资料分析,微差爆破振动信号具有持时短、衰减快以及时频局部化的特点,属于典型的非平稳信号。长期以来限于理论的发展,只好将微差爆破振动信号视为简单的平稳信号,分析和处理平稳信号最常用的方法是Fourier分析。近年来,随着科学技术的发展,小波时频局部化分析已广泛应用于工程技术领域,用小波时频局部化分析和处理非平稳信号已激起人们很高的热忱[3]。小波时频局部化分析方法是一种窗口大小固定但其形状、时频窗都可改变的时频局部化分析方法[4]。小波时频局部化分析技术在微差爆破振动信号特征提取、频谱分析、微差延期时间识别、波形预测和反应谱分析等方面具有良好的应用效果[5]。然而,采用经典小波进行小波时频局部化分析时,往往是根据研究对象的特点从已有的Matlab小波分析工具箱中选择一个比较合适的小波基,虽然可以满足微差爆破振动信号分析处理的一般要求,但由于小波基以及尺度选取的不确定性事实,已严重影响了小波时频局部化分析的实际应用效果[6-8]。因此,如何根据微差爆破振动信号的特征选择或构造与特征信号更好匹配的最优小波基、提高信号处理的效率与质量是小波理论在爆破振动信号分析中亟待解决的问题[9-13]。

本文以此为切入点,在模式自适应小波原理的基础上,运用时频转换技术,将实测微差爆破振动信号分离出子信号并对其进行模式自适应波形匹配,构造出与子信号相似度高的模式自适应爆破振动信号小波基(简称模式自适应小波,下同),然后将该模式自适应小波添加到Matlab小波分析工具箱中,并提出一种新的基于爆破振动信号小波时频局部化分析的模式自适应小波时能密度法,将其用于实验设计信号和实测微差爆破振动信号的微差延期时间识别,取得了满意的结果,从而为爆破振动信号分析在实际工程中的应用提供参考。

1 模式自适应小波时能密度法

1.1 连续小波变换

函数ψ(t)∈L2(R)(L2(R)为平方可积的信号空间)的连续傅里叶变换为ψ^(ω)[14-16]。当ψ^(ω)满足小波允许条件：

时,称ψ(t)为一个小波基。若将该小波基ψ(t)经伸缩和平移后,就得到一个小波基序列。

对于实数a,b且a≠0的情况下,小波基序列为

式中,a为尺度因子;b为平移因子。

对于微差爆破振动信号f(t)∈L2(R)的连续小波变换为

由式(2)可以看出,小波变换的实质是将微差爆破振动信号f(t)与小波基序列ψa,b(t)做卷积,求得微差爆破振动信号f(t)在小波基序列ψa,b(t)上的投影。若要微差爆破振动信号中的特征成分在小波系数时频谱上更好地显示,则需要将微差爆破振动信号f(t)在小波基序列ψa,b(t)上的投影系数尽可能地最大化,也就是说小波基的波形应与微差爆破振动信号特征波形具有较高的相似度。

1.2 模式自适应小波

模式自适应小波是利用最小平方优化方法来构建一个与给定模式近似的小波[17]。具体方法有多项式逼近法(polynomial)和常数正交函数空间投影法(orth．and constants)2种。如果信号特征模式比较简单,则可以选择多项式逼近法;如果信号特征模式比较复杂,则可以选择常数正交函数空间投影法。参数规则度(regularity)定义了模式自适应小波在[0, 1]上的边界约束,可以是“无”或“连续”或“可微”。

基于上述构造模式自适应小波的思想[18-19],提出了以下步骤：

(1)根据给定的检测模式f,产生模式自适应小波ψf(t)。不失一般性,假设supp(f)=[0,1],则有

(2)检测信号上所有的报警,对任意b和a＞0的问题,搜索信号小波能量的局部极大值。

(3)检测和丢弃所有错误的报警,这一规则必须应用于确定每个报警是否错误。

1.3 模式自适应小波时能密度法

若模式自适应小波满足式(1)的容许性条件,则说明模式自适应小波变换是完备的并且保持能量守恒,根据Moyal定理,有下式成立

式(3)表明模式自适应小波变换系数平方的积分同被分析的微差爆破振动信号的能量成正比。因此,可以把看作是模式自适应小波时间-尺度平面上的模式自适应小波能量密度函数,即给出了以尺度因子a和平移因子b为中心的、尺度间隔为Δa、时间间隔为Δb的能量。根据模式自适应小波能量密度的概念,式(3)也可以写成

在模式自适应小波变换中,尺度因子a在某种程度上对应于实际频率f,因此,式(5)给出了微差爆破振动信号所有频带的能量随平移因子b的分布情况,称为模式自适应小波时能密度函数。

2 模式自适应小波时能密度法的构造、添加与实现

2.1 可行性分析

从理论上讲,任何函数f(x)∈L2(R)只要满足小波基允许条件就能作为一个新的小波基进行选用,但选择具有紧支撑性、一定正则性、曲线外形与微差爆破振动信号有较好相似性的函数作为小波基函数,能在时频域上都取得良好的时频局部化分析效果。从某一实测微差爆破振动信号中分离出的子信号速度-时间曲线如图1所示及其相应的功率谱曲线见图2[5]。从图1,2可以看出,爆破振动子信号在时频域上能量都比较集中、且衰减速度较快,也就是说爆破振动子信号在时频域上均具有良好的时频局部化特性。因此,可以根据微差爆破振动信号的特点,由爆破振动子信号来进行模式自适应波形匹配,构造出与爆破振动子信号相似度高的模式自适应小波。

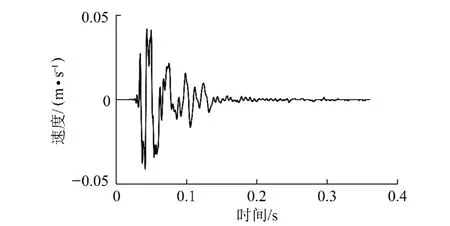
图1 子信号的速度-时间曲线Fig．1 The velocity vs time curve of blast vibration sub-signal

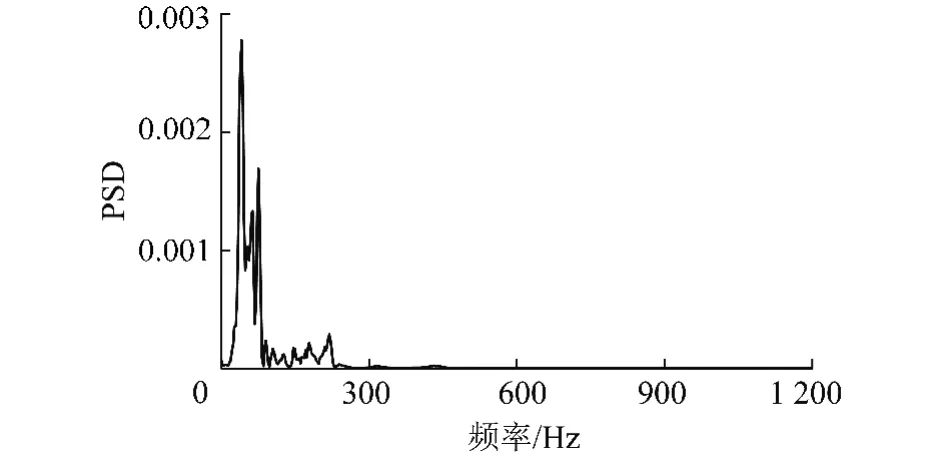
图2 子信号的频谱图Fig．2 Spectrogram of blast vibration sub-signal

2.2 模式自适应小波的构造

在Matlab语言环境下,通过利用Wavelet Toolbox工具箱中的New Wavelet for CWT界面对如图1所示的爆破振动子信号进行模式自适应波形匹配,构造出与爆破振动子信号相似度高的sub_signal．mat函数(其中与原始信号的相关系数高达0．99)。构造好的模式自适应小波如图3所示。

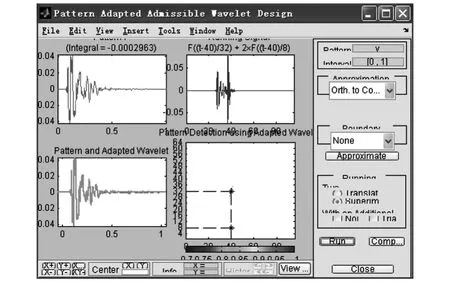
图3 子信号的模式自适应小波设计Fig．3 Pattern adapted admissible wavelet design of blast vibration sub-signal

2.3 模式自适应小波的添加

在Matlab编程语言工作平台上,可以使用wavemngr命令添加该模式自适应小波[20]。添加好的模式自适应小波显示如图4所示。

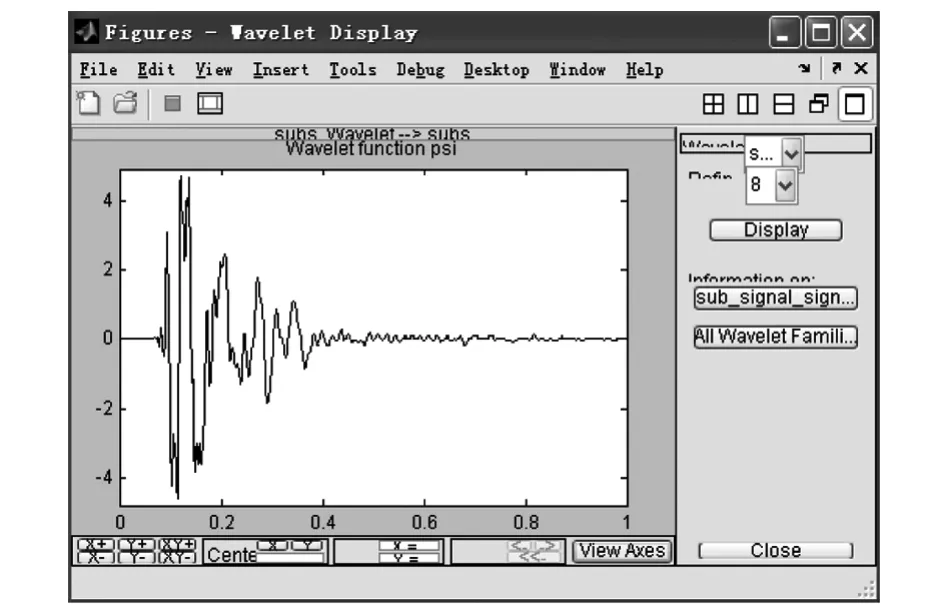
图4 子信号的模式自适应小波显示Fig．4 Pattern adapted admissible wavelet display of blast vibration sub-signal

2.4 模式自适应小波时能密度法的实现

2.4.1 模式自适应小波的实现

爆破振动信号延期时间识别在时间上观察得愈细致,就愈需要压缩观察范围,即用高频小波作细致的观察和提取,故应选用较小的尺度。模式自适应小波基函数支撑区间为[0,1],Matlab中的CWT算法无法实现模式自适应小波基函数尺度小于1的情况,因此,有必要采用数值积分的方法。

将式(2)中的时间t和平移因子b作离散处理,按照数字信号处理的习惯把时间t离散为jTs,把平移因子b离散为iTs,其中Ts是采样时间,则式(2)可变为

其中,dt为采样时间间隔,取dt=Ts,式(6)可变为

其中,f(jdt)为微差爆破振动信号按照采样时间间隔dt连续采集的数据。式(7)小波变换的结果可存放在计算机设定数组中,即实现了模式自适应小波变换。

2.4.2 模式自适应小波时能密度法的实现

采用模式自适应小波作为基函数,选取合适的起始尺度以及尺度间隔,对实验设计信号和实测微差爆破振动信号进行模式自适应小波时能密度法分析,根据模式自适应小波时能密度曲线中出现的奇异点位置即可得到各段雷管的实际起爆时刻,从而可以识别出微差爆破的实际延迟时间。模式自适应小波时能密度法的流程如图5所示。

图5 模式自适应小波时能密度法的流程Fig．5 Flowchart of pattern adapted wavelet time-energy density method

3 实验设计与分析

3.1 实验设计

图6为爆破振动子信号在0～80 ms内每隔20 ms进行一段波形叠加而构成的多段微差爆破振动信号,各分段微差爆破振动信号出现的时刻分别为0,20,40,60,80 ms,若多段微差爆破振动信号的采样频率为5 000 Hz,则多段微差爆破振动信号的采用时间间隔为1/5 000 s=0．2 ms,这样各分段微差爆破振动信号出现的时刻又可以用相应的时间序列位置来表示,也就是说各分段微差爆破振动信号出现的时间序列位置分别为0,100,200,300,400。若将最低段次雷管产生的多段微差爆破振动信号表示为x(n),则其他各分段微差爆破振动信号可以分别表示为x(n-100),x(n-200),x(n-300),x(n-400),叠加后的多段微差爆破振动信号则可以表示为

式中,y(n)为叠加后的多段微差爆破振动信号;x(nnm)为不同微差间隔下的分段微差爆破振动信号;m为爆破振动子信号的条数。

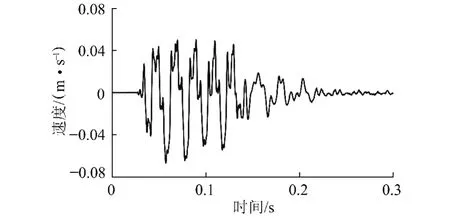
图6 信号y(n)的速度-时间曲线Fig．6 The velocity vs time curve of signal y(n)

3.2 结果分析

由于多段微差爆破振动信号y(n)是在爆破振动子信号x(n)的基础上进行4次信号叠加而成,每次爆破振动子信号的叠加都会引起多段微差爆破振动信号y(n)的局部能量的突变,因此,可采用小波变换模极大值法识别出每次爆破振动子信号叠加的时刻,从而确定多段微差爆破振动信号y(n)中各相邻爆破振动子信号间的实际微差延期时间间隔。目前,在微差爆破振动信号小波变换模极大值法中用得最多的是db8小波,本文也选用db8小波[21]。在Matlab小波分析工具箱中分别选用db8小波、模式自适应小波对多段微差爆破振动信号y(n)进行连续小波变换并取模值,结果见表1和图7(a),(b)。图7(c)为采用模式自适应小波作为基函数,尺度因子下限为0．1、上限为10和间隔为0．1时多段微差爆破振动信号y(n)的模式自适应小波时能密度曲线。

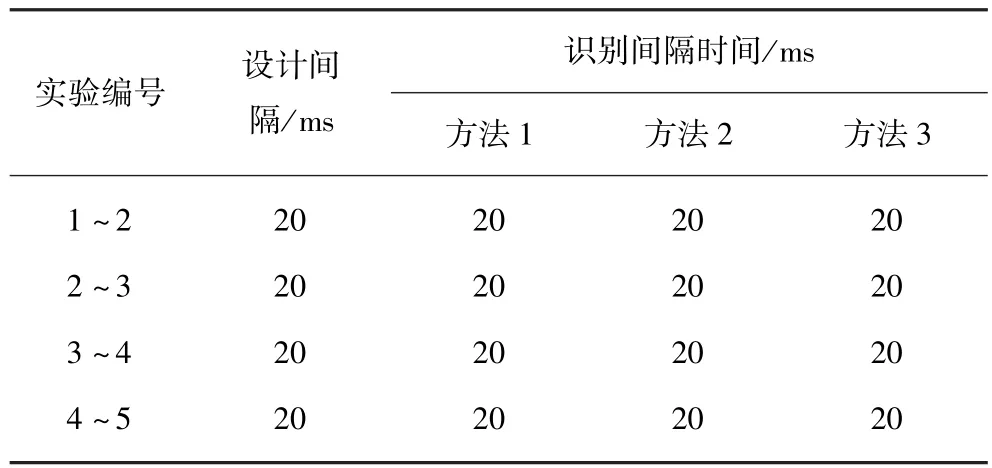
表1 采用3种方法对实验信号的识别效果比较Table 1 Comparison of identification effect for experiment signals by three different methods

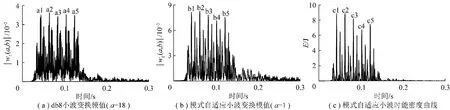
图7 信号y(n)的db8小波、模式自适应小波变换模值以及模式自适应小波时能密度曲线Fig．7 db8 wavelet,pattern adapted wavelet transform modulus and pattern adapted wavelet time-energy density curve of signal y(n)

从表1、图7可以清楚地看出,多段微差爆破振动信号y(n)的db8小波、模式自适应小波变换模极大值以及模式自适应小波时能密度曲线中均出现了5个奇异点,位置分别为0．044 4,0．064 4,0．084 4, 0．104 4,0．124 4和0．042 4,0．062 4,0．082 4, 0．102 4,0．122 4以及0．042 4,0．062 4,0．082 4, 0．102 4,0．122 4 s,表明该多段微差爆破振动信号是由5段爆破振动子信号叠加而成。由于微差爆破延期时间间隔是前后两段雷管起爆时刻间的时间间隔,若将第1个奇异点位置作为最低段次雷管的起爆时刻,则该批次雷管的实际起爆时刻均为0,20,40,60, 80 ms,段间微差延期时间间隔均为20 ms。由此可以表明,db8小波法、模式自适应小波法以及模式自适应小波时能密度法对多段微差爆破振动信号y(n)中各分段爆破振动子信号的延期时间间隔识别效果较理想,可以有效识别多段微差爆破振动信号中的各奇异点位置。同时,方法2和方法3得到的多段微差爆破振动信号奇异点位置是完全相同的,由此表明模式自适应小波时能密度法分析微差爆破振动信号的设计时间间隔是完全可靠的。

4 实例分析

采用爆破振动分析仪和速度传感器对某地下矿进行多次微差爆破振动信号测试,图8为从中抽取的一条爆破振动速度-时间曲线,分别采用db8小波法、模式自适应小波法以及模式自适应小波时能密度法(其中尺度下限为0．1、上限为10和间隔为0．1)对其进行分析处理,结果如图9所示。

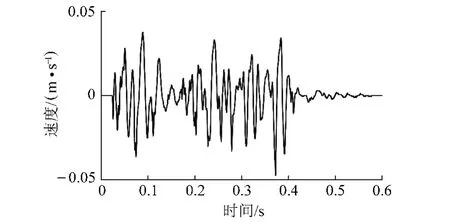
图8 爆破振动信号的速度-时间曲线Fig．8 The velocity vs time curve of blast vibration signal

从图9可以清楚地看出,微差爆破振动信号的db8小波、模式自适应小波变换模值以及模式自适应小波时能密度曲线中均出现了6个奇异点,位置分别为0．044 8,0．082 4,0．208 4,0．245 6,0．306 0,0．344 0和0．042 8,0．082 4,0．198 8,0．248 8,0．296 4,0．346 0以及0．042 8,0．082 4,0．198 4,0．250 0,0．296 0, 0．346 0 s,段间微差延期时间间隔分别为37．6, 126．0,37．2,60．4,38．0和39．6,116．4,50．0,47．6, 49．6以及39．6,116．0,51．6,46．0,50．0 ms。分别将db8小波法、模式自适应小波法以及模式自适应小波时能密度法得到的实际微差延期时间间隔与雷管的设计延期时间间隔进行比较(表2)。

图9 微差爆破振动信号的db8小波、模式自适应小波变换模值以及模式自适应小波时能密度曲线Fig．9 db8 wavelet,pattern adapted wavelet transform modulus and pattern adapted wavelet time-energy density curve of measured millisecond blast vibration signal

表2 采用3种方法对微差爆破振动信号的识别效果比较Table 2 Comparison of identification effect for millisecond blast vibration signals by three different methods

从表2可以看出,采用3种不同小波分析法得到的2～4段次、5～6段次、6～7段次雷管起爆的实际微差延期时间间隔均在设计微差延期时间间隔范围内,属正常起爆;而4～5段次、7～9段次雷管起爆的实际微差延期时间间隔均超出了设计微差延期时间间隔范围,属非正常起爆。由此表明4～5段次、7～9段次雷管进行微差爆破时需谨慎使用。虽然3种不同小波分析法对同一微差爆破振动信号进行微差延期时间间隔的识别,效果均较理想,但通过图9的比较不难看出,模式自适应小波法的分辨率要比db8小波法的高,表明在微差爆破振动信号的奇异性检测方面,基于爆破振动子信号的模式自适应小波法比Matlab工具箱已有小波法的效果好,具有较好的突出微差爆破振动信号奇异点的位置,从而验证了将爆破振动子信号作为爆破振动信号分析中的小波基是可行的,解决了适合爆破振动信号特征的小波基构造、添加及其实现等问题,为分析微差爆破振动信号时选择以及优化小波基提出了一种新的方法。同时,模式自适应小波时能密度法比模式自适应小波法分辨率更高,压制了随机噪声的干扰,突出了爆破振动信号奇异点位置,提高了爆破振动信号处理的效率与质量。

5 结 论

(1)在模式自适应连续小波原理的基础上,构造了从实测微差爆破振动信号中分离出子信号的爆破振动信号小波基,然后将该爆破振动信号小波基添加到Matlab小波分析工具箱中,从而解决了适合爆破振动信号特征的小波基构造与添加及实现等问题,并提出了一种新的基于爆破振动信号小波分析的模式自适应小波时能密度法,并且该方法能够自适应产生“基”,即不需要任何先验基函数。

(2)通过微差延期时间间隔下的多段微差爆破振动信号验证了模式自适应小波时能密度法在微差爆破振动信号分析中的可行性,然后在工程实例中比较了db8小波法、模式自适应小波法以及模式自适应小波时能密度法在微差起爆延时间隔的实际应用效果,结果表明基于爆破振动信号特征的模式自适应小波法、模式自适应小波时能密度法在确定爆破振动信号微差延时方面比db8小波法效果更理想,且模式自适应小波时能密度法比模式自适应小波法分辨率更高,更好的突出了爆破振动信号奇异点位置,提高了爆破振动信号处理的效率与质量,从而为小波理论在爆破工程实际中的应用研究奠定了基础。

[1] 韩 博,马芹永．煤矿岩巷毫秒延期爆破振动测试与控制技术研究[J]．煤炭学报,2013,38(2)：209-214．

Han Bo,Ma Qinyong．Research on testing and controlling techniques of millisecond delay blasting vibration in coal mine roadway[J]．Journal of China Coal Society,2013,38(2)：209-214．

[2] 凌同华,李夕兵．基于小波变换的时-能分布确定微差爆破的实际延迟时间[J]．岩石力学与工程学报,2004,23(13)：2266-2270．

Ling Tonghua,Li Xibing．Time-energy analysis based on wavelet transform for identifying real delay time in millisecond blasting[J]．Chinese Journal of Rock Mechanics and Engineering,2004,23 (13)：2266-2270．

[3] 凌同华,廖艳程,张 胜．冲击荷载下岩石声发射信号能量特征的小波包分析[J]．振动与冲击,2010,29(10)：127-130．

Ling Tonghua,Liao Yancheng,Zhang Sheng．Application of wavelet packet method in frequency band energy distribution of rock acoustic emission signals under impact loading[J]．Journal of Vibration and Shock,2010,29(10)：127-130．

[4] 赵明生,梁开水,余德运,等．段数对爆破振动信号的时频特性影响分析[J]．煤炭学报,2012,37(1)：55-61．

Zhao Mingsheng,Liang Kaishui,Yu Deyun,et al．Effect of segments on time frequency characteristics of blasting vibration signals[J]．Journal of China Coal Society,2012,37(1)：55-61．

[5] 李夕兵,凌同华,张义平．爆破震动信号分析理论与技术[M]．北京：科学出版社,2009：66-81．

[6] 李 臻．自适应提升小波的构造及其在齿轮箱早期故障诊断中的应用[J]．煤炭学报,2010,35(S)：228-231．

Li Zhen．The construction of adaptive lifting wavelet and its application in incipient fault diagnosis of gearbox[J]．Journal of China Coal Society,2010,35(S)：228-231．

[7] 凌同华．爆破震动效应及其灾害的主动控制[D]．长沙：中南大学,2004：34-52．

[8] 刘 高．深部大规模爆破振动信号分析与灾害控制研究[D]．长沙：中南大学,2011：44-57．

[9] 耿艳峰,冯叔初．小波构造综述[J]．石油大学学报(自然科学版),2004,28(1)：127-131．

Geng Yanfeng,Feng Shuchu．Overview of wavelet construction[J]． Journal of the University of Petroleum,China(Edition of Natural Science),2004,28(1)：127-131．

[10] 宋光明．爆破振动小波包分析理论与应用研究[D]．长沙：中南大学,2001：18-30．

[11] 李春庚．自适应小波的构造及其在信号处理中的应用[D]．大连：大连海事大学,2007：1-16．

[12] 陈倩倩．基于岩土工程信号特征的小波基构造及其算法与实现研究[D]．长沙：长沙理工大学,2013：1-9．

[13] 丁爱玲,石光明,张 宁,等．波形匹配小波设计及其在信号数据压缩中的应用[J]．电子与信息学报,2007,29(4)：804-807．

Ding Ailing,Shi Guangming,Zhang Ning,et al．Signal compression and design of wavelet based on waveform matching[J]．Journal of Electronics&Information Technology,2007,29(4)：804-807．

[14] 程正兴,杨守志,冯晓霞．小波分析的理论、算法、进展和应用[M]．北京：国防工业出版社,2007：1-11．

[15] 张锐戈,谭永红．基于最优Morlet小波和隐马尔可夫模型的轴承故障诊断[J]．振动与冲击,2012,31(12)：5-8,27．

Zhang Ruige,Tan Yonghong．Fault diagnosis of rolling element bearings based on optimal morlet wavelet and hidden markov model [J]．Journal of Vibration and Shock,2012,31(12)：5-8,27．

[16] 栗茂林,梁 霖,王孙安,等．基于连续小波系数非线性流形学习的冲击特征提取方法[J]．振动与冲击,2012,31(1)：106-111,126．

Li Maolin,Liang Lin,Wang Sun’an,et al．Mechanical impact feature extraction method based on nonlinear manifold learning of continuous wavelet coefficients[J]．Journal of Vibration and Shock, 2012,31(1)：106-111,126．

[17] 张煜东,朱 庆,陈贤卿,等．基于模式的自制小波在EBPSK信号检测中的应用[J]．东南大学学报(自然科学版),2011, 41(4)：691-694．

Zhang Yudong,Zhu Qing,Chen Xianqing,et al．Pattern-based custom wavelet used for EBPSK signal detection[J]．Journal of Southeast University(Natural Science Edition),2011,41(4)：691-694．

[18] Mesa H．Adapted wavelets for pattern detection[A]．Progress in Pattern Recognition,Image Analysis and Applications[C]．Springer Berlin Heidelberg,2005：933-944．

[19] Chapa J O,Rao R M．Algorithms for designing wavelets to match a specified signal[J]．IEEE Transactions on Signal Processing, 2000,48(12)：3395-3406．

[20] 胡昌华,李国华,周 涛．基于MATLAB 7．x的系统分析与设计—小波分析(第三版)[M]．西安：西安电子科技大学出版社,2008：236-245．

[21] 严 鹏,卢文波,罗 忆,等．基于小波变换时-能密度分析的爆破开挖过程中地应力动态卸载振动到达时刻识别[J]．岩石力学与工程学报,2009,28(S1)：2836-2844．

Yan Peng,Lu Wenbo,Luo Yi,et al．Identification of arriving time of vibration induced by geostress dynamic unloading during blasting-excavation employing method of time-energy analysis based on wavelet transform[J]．Chinese Journal of Rock Mechanics and Engineering,2009,28(S1)：2836-2844．

Pattern adapted wavelet time-energy density method and its application in millisecond blast vibration signal analysis

ZHANG Sheng1,2,LING Tong-hua1,LIU Hao-ran1,CAO Feng1

(1.School of Civil Engineering and Architecture,Changsha University of Science&Technology,Changsha 410114,China;2.Key Laboratory for Safety Control of Bridge Engineering,Ministry of Education and Hunan Province,Changsha University of Science&Technology,Changsha 410114,China)

How to solve wavelet basis construction,addition,realization and other issues that suitable for characterizing blast vibration signal is a challenge for many researchers．To determine real millisecond delay time of millisecond blast vibration signal accurately,a pattern adapted wavelet basis separated from measured millisecond blast vibration signal was constructed based on the principle of pattern adapted wavelet．The pattern adapted wavelet basis was added to Wavelet Toolbox in Matlab,and a new pattern adapted wavelet time-energy density method was proposed based on blast vibration signal analysis．The feasibility of the method was verified with the pattern adapted wavelet time-energy density method of millisecond blast vibration signal for experimental design．The method can also be used to analyze the measured millisecond blast vibration signal to determine real millisecond delay time．Compared with db8 wavelet method and with pattern adapted wavelet method,the results indicate that the pattern adapted wavelet time-energy density method has a better application effect．Thereby,the method provides a reference for blast vibration signal analysisin practical engineering application．

blast vibration;millisecond time;pattern adapted wavelet time-energy density method;wavelet basis construction;wavelet basis addition

TD235

A

0253-9993(2014)10-2007-07

2014-03-14 责任编辑：常 琛

国家自然科学基金资助项目(51278071);湖南省研究生科研创新资助项目(CX2013B368);长沙理工大学桥梁工程安全控制省部共建教育部重点实验室开放基金资助项目(13KB03)

张 胜(1984—),男,湖南益阳人,博士研究生。E-mail：zhangsheng0403311@163．com。通讯作者：凌同华(1968—),男,湖南双峰人,教授,博士生导师,博士。E-mail：lingtonghua@163．com

张 胜,凌同华,刘浩然,等．模式自适应小波时能密度法及其在微差爆破振动信号分析中的应用[J]．煤炭学报,2014,39(10)： 2007-2013．

10．13225/j．cnki．jccs．2014．0325

Zhang Sheng,Ling Tonghua,Liu Haoran,et al．Pattern adapted wavelet time-energy density method and its application in millisecond blast vibration signal analysis[J]．Journal of China Coal Society,2014,39(10)：2007-2013．doi：10．13225/j．cnki．jccs．2014．0325