盐岩蠕变特性及其非线性本构模型

王军保,刘新荣,郭建强,黄 明

(1.西安建筑科技大学土木工程学院,陕西西安 710055;2.重庆大学土木工程学院,重庆 400045;3.福州大学土木工程学院,福建福州350108)

盐岩蠕变特性及其非线性本构模型

王军保1,2,刘新荣1,2,郭建强2,黄 明3

(1.西安建筑科技大学土木工程学院,陕西西安 710055;2.重庆大学土木工程学院,重庆 400045;3.福州大学土木工程学院,福建福州350108)

为了研究盐岩的蠕变特性,利用RLW－2000岩石流变试验机对盐岩试件进行了三轴压缩分级加载蠕变试验。试验结果表明:在围压一定的情况下,随着轴向应力增大,盐岩瞬时应变、蠕变应变以及蠕变速率等均随之增大,同时进入稳态蠕变阶段所需要的时间逐渐延长;等时应力－应变曲线显示,盐岩蠕变具有非线性特征,且其非线性程度与蠕变时间和应力水平有关,蠕变时间越长、应力水平越高,非线性程度越高。基于非线性流变力学理论,提出了一种非线性黏滞体,其黏滞系数是所加应力水平和蠕变时间的函数,将非线性黏滞体替换常规Burgers模型中的线性黏滞体,建立了可描述盐岩非线性蠕变特性的MBurgers模型,并根据盐岩蠕变试验结果,采用曲线拟合法对MBurgers模型的参数进行了反演识别。拟合曲线和试验曲线对比显示,两者吻合良好,误差较小,说明该模型可以描述盐岩的蠕变特性。

盐岩;蠕变特性;非线性模型;参数识别

Key words:salt rock;creep properties;nonlinear model;parameters identification

蠕变特性作为盐岩典型的力学性质之一,是影响盐岩地下储存库长期稳定性、安全性以及可用性的关键因素。由于盐岩在能源地下储存方面的重要地位,近年来国内外学者对盐岩蠕变特性及其本构模型进行了较多研究。Asanov[1]研究了盐岩的剪切蠕变特性。李萍等[2]对不同矿物成分的盐岩进行了蠕变试验,分析了矿物成分和应力水平等对盐岩蠕变性的影响。陈锋等[3]研究了云应盐矿两种盐岩的蠕变特性,并提出了盐岩稳态蠕变本构关系。Chan[4]等提出了盐岩蠕变、损伤断裂多机制藕合本构模型(MDCF模型)。Wang、马林建等[5－6]在Carter蠕变模型基础上建立了盐岩蠕变损伤模型。杜超等[7]指出盐岩的蠕变变形是应变硬化和回复效应等内部变形机制共同作用的结果,并选用内应力作为内变量建立了盐岩蠕变模型。此外,许多学者采用黏弹塑性元件组合模型理论来描述盐岩的蠕变响应。唐明明等[8]用Burgers模型反映盐岩在稳态蠕变阶段的变形特性。郤保平等[9]采用由5元件广义开尔文模型和宾汉姆模型串联组成的黏弹塑性蠕变模型来对盐岩试验结果进行拟合。刘江等[10]依据盐岩蠕变试验结果,提出了由马克斯威尔体和廖国华体串联组成的黏弹塑性本构模型。Zhou等[11]提出了基于分数阶导数的岩盐蠕变本构模型。

从整个岩石力学流变领域来看,元件组合模型由于本构方程形式简单,参数物理意义明确,且能够把岩石复杂的力学性质直观的表现出来,因而近年来得到了广泛应用。但传统的元件组合模型是一种线性模型,无法描述岩石蠕变的非线性特征,而对于大多数岩石来说,其蠕变过程具有非线性特征,这一点已被众多文献所证实。为了改进传统元件组合模型无法反映岩石非线性蠕变特征的不足,一种有效的方法就是采用非线性流变元件代替常规线性流变元件,并据此建立能够反映岩石非线性特征的蠕变模型[12－16]。目前,在这方面关于盐岩的研究成果还不多见。

本文拟在对盐岩蠕变试验结果进行分析的基础上,结合非线性元件组合模型理论建立盐岩非线性蠕变模型,以期为盐岩地下储存库的长期稳定性分析和安全性评价等提供一定的借鉴和参考。

1 盐岩三轴压缩蠕变试验

1.1 试验概况

试验所用盐岩试样取自江苏淮安某盐矿,主要成分为NaCl,质地较纯,呈白色、灰白色,部分略带灰黑色不溶物杂质,天然密度为2.15～2.22 g/cm3。按照岩石力学试验标准的要求,将岩样加工成直径50 mm,高度100 mm的圆柱形标准试件。由于盐岩具有遇水溶解的特点,为了避免试件加工过程中水对盐岩结构的破坏和盐岩溶解,采用手工打磨的方法进行加工。

试验仪器采用长春朝阳仪器厂生产的RLW－2000岩石流变试验机。该设备主要由机架、轴向稳压系统、侧向稳压系统、数字控制系统及微机系统等5部分组成,采用先进的伺服控制、滚珠丝杠和液压等技术组合,达到了良好的稳压效果,可进行单轴压缩试验、三轴压缩试验、蠕变试验、松弛试验、渗流试验以及循环荷载试验等。设备最大轴向荷载2 000 kN,有效测力范围10～2 000 kN,测力分辨率20 N,测力误差≤0.5%;最大围压60 MPa,围压测量误差≤1%,分辨率0.001 MPa。

1.2 试验结果及分析

对2个盐岩试件分别进行了围压10 MPa和围压15 MPa下的分级加载蠕变试验,轴向分级加载应力均为20,25和30 MPa。图1给出了将这两个岩样分级加载蠕变曲线进行处理后得到的分别加载蠕变曲线簇。

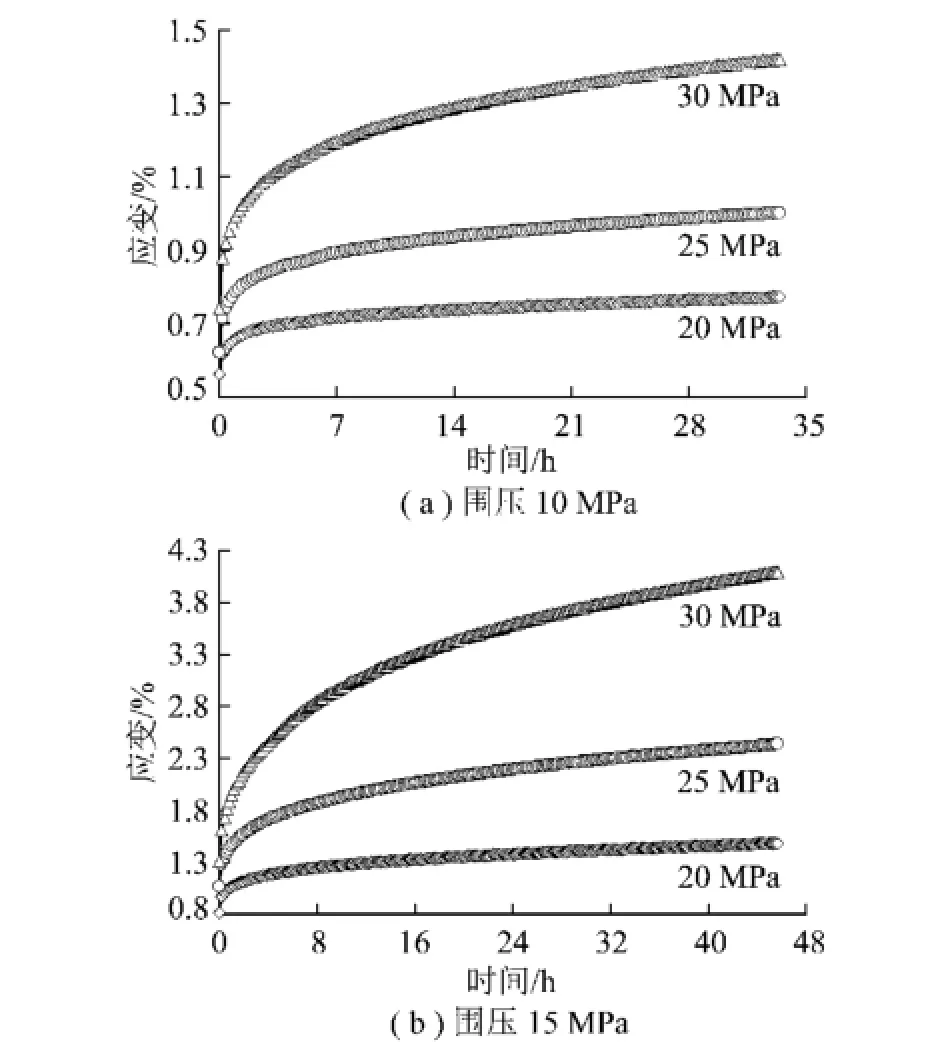
图1 不同围压下盐岩分别加载蠕变曲线簇Fig.1 Creep curves of salt rock under different confining pressure

由图1可以看到:

(1)盐岩在各级荷载作用下的应变均由加载过程产生的瞬时应变、衰减蠕变应变以及蠕变速率较为稳定的稳态蠕变应变3部分组成。由于试验所施加的最高应力未达到使岩样发生加速蠕变的临界应力,且受试验条件限制,加载时间不够长,2个盐岩试件均未出现加速蠕变阶段。

(2)在围压一定的情况下,总体上瞬时应变、蠕变应变以及稳态蠕变率均随轴压增加而增大。以围压15 MPa岩样的试验结果为例,经过约46 h的蠕变后,轴压为20 MPa时,瞬时应变为0.812 3%,蠕变应变为0.674 6%,稳态蠕变率为4.3×10－5h－1;轴压为25 MPa时,瞬时应变增加为1.065 1%,蠕变应变增加为1.367 4%,稳态蠕变率增加为9.6×10－5h－1;而当轴压为30 MPa时,瞬时应变达到1.314 4%,蠕变应变达到2.786 9%,稳态蠕变率则达到2.1× 10－4h－1。当轴压从20 MPa增加到25 MPa和30 MPa时,瞬时应变、蠕变应变以及稳态蠕变率分别增加为原来的1.31,2.03,2.23倍和1.62,4.13,4.88倍。可见,在围压一定的情况下,由于轴压增加,偏应力增大,导致盐岩瞬时应变、蠕变应变和蠕变速率均有不同程度的增大。

(3)在围压一定的情况下,轴压越大,衰减蠕变阶段曲线的曲率半径越大,经历的时间越长,达到稳态蠕变的时间越晚。仍以围压15 MPa岩样的试验结果为例,轴压为20 MPa时,加载约12 h蠕变达到近似稳态蠕变阶段;当轴压为25 MPa时,加载约20 h蠕变达到近似稳态蠕变阶段;而当轴压为30 MPa时,经过约32 h蠕变才达到近似稳态蠕变阶段。

根据岩盐蠕变试验数据可作出其等时应力－应变曲线,图2给出了围压15 MPa岩样的等时应力－应变曲线。

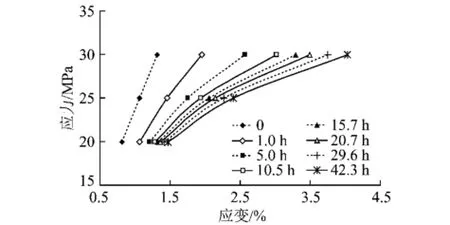
图2 围压15 MPa岩样等时应力－应变曲线Fig.2 Isochronous stress-strain curves of salt rock with confining pressure 15 MPa

由图2可见,不同时刻的等时应力－应变曲线形状不同。当时间为0时,等时应力－应变曲线近似为直线,因此,可认为盐岩瞬时应变以弹性变形为主;当时间不为0时,随着蠕变时间延长,等时应力－应变曲线逐渐偏离直线向应变轴弯曲,且蠕变时间越长等时曲线偏离直线的程度越高,向应变轴弯曲越明显。同时,对于某一时刻来说,等时应力－应变曲线向应变轴弯曲的程度还与应力水平有关,应力水平越高,曲线向应变轴弯曲越明显。由此可以看出,盐岩具有非线性蠕变特征,且其非线性程度与蠕变时间和应力水平有关,蠕变时间越长、应力水平越高,非线性程度越高。

2 盐岩非线性蠕变模型

2.1 非线性黏滞体的引入

在传统的元件组合模型中,通常认为岩石材料的蠕变参数是固定不变的常数,因而无法反映其非线性蠕变特征[13]。根据前面对盐岩蠕变试验结果的分析可知,盐岩具有非线性蠕变特征,且其非线性程度与蠕变时间和应力水平有关。因此,为了更好地描述盐岩的非线性蠕变特征,本文引入了一个非线性黏滞体,其黏滞系数是所加应力水平和蠕变时间的函数。

对于岩石蠕变的前两个阶段,即衰减蠕变和稳态蠕变阶段,研究表明[17]岩石黏滞系数将随时间增加而发生硬化增大。因此,本文假定该非线性黏滞体黏滞系数随时间的变化过程符合下式

由式(1)可知,当t=0时,η(0)=0;当t→∞时, η(t)→η0。这说明当t从0→∞时,η(t)从0单调递增至η0。黏滞系数增大会导致岩石蠕变速率逐渐减小,这与文献[17]等描述的岩石黏滞系数变化规律较为符合。理论上只有当t→∞时,η(t)才会达到η0;而实际上由于参数m为一有限值,当时间增加到一定程度以后,m/(2 t)已经趋近于0,此时η(t)也已接近其最大值η0。另外,当t=0时,η(0)=0,这会导致荷载施加瞬间,岩石蠕变速率为无穷大。实际上,在加载过程中,岩石黏滞系数的硬化增大过程已经发生,因此在实际应用时可将起始蠕变时间取一个接近于0的极小值。

式(1)反映了蠕变时间对非线性黏滞体黏滞系数的影响,在式(1)基础上引入表征应力水平对黏滞系数影响的函数[15]

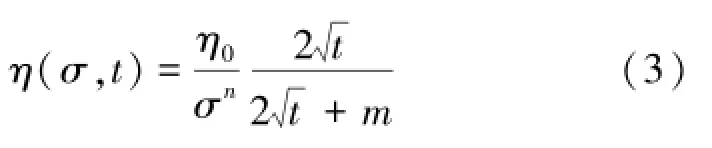
式中,σ为应力;n为材料参数。

由式(3)可知,对于某一不为0的时刻来说,此时时间t为定值,随着应力σ增大,η(σ,t)逐渐减小,从而导致蠕变变形逐渐增大。反映到等时应力－应变曲线上就是,在某一不为0的时刻,应力水平越高,等时曲线的非线性程度越高,向应变轴弯曲越明显,这与实际情况较为符合。

同时由式(3)可以看出,η(σ,t)的变化过程是应力σ和时间t综合作用的结果。将η(σ,t)代替传统黏滞体元件本构方程中的黏滞系数η,可得本文非线性黏滞体的本构方程为

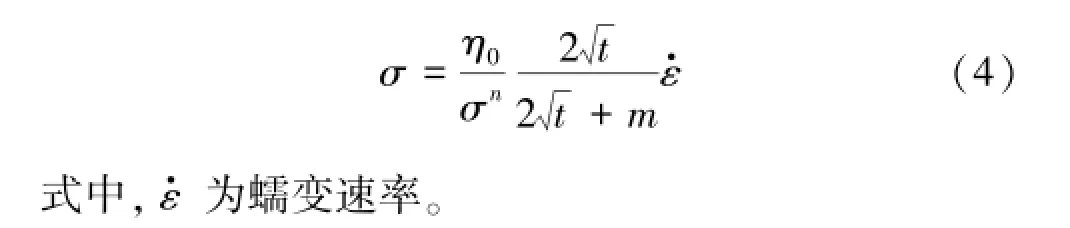
2.2 非线性蠕变模型的建立

由盐岩蠕变试验结果可知,盐岩蠕变曲线与Burgers模型蠕变曲线较为相似,但常规Burgers模型无法反映盐岩蠕变的非线性特征。为了更好地描述盐岩非线性蠕变特征,本文将上面得到的非线性黏滞体代替常规Burgers模型的线性黏滞体,从而构成了改进的非线性Burgers模型,本文将其命名为MBurgers模型,模型如图3所示。

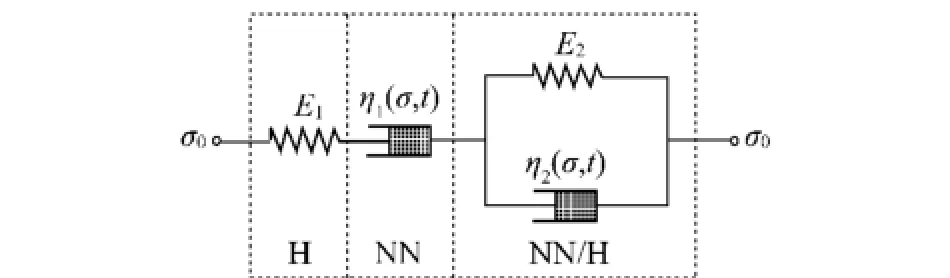
图3 MBurgers模型示意Fig.3 Schematic view of MBurgers model

由图3可见,MBurgers模型由弹性体(H)、非线性黏滞体(NN)和非线性Kelvin体(NN/H)串联组成,分别描述盐岩加载的瞬时变形、黏性变形和黏弹性变形。由于模型中3部分串联,则有

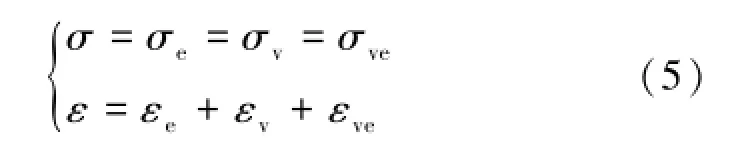
式中,σ和ε分别为模型总应力和总应变;σe,εe,σv, εv,σve,εve分别为H体、NN体和NN/H体对应的应力和应变。

在t=0时刻,对模型施加恒定应力σ0,则有:

(1)对于H体,其本构关系为

式中,E1为H体弹性模量。

(2)对于NN体,结合式(4),可得其本构方程为

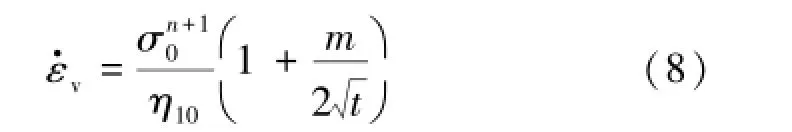
将式(8)对时间积分,并考虑初始条件:t=0,εv= 0,则有

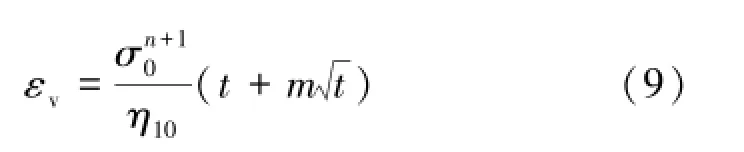
式(7)变形可得

式(9)即为NN体的蠕变方程。

(3)对于NN/H体,结合常规Kelvin体本构方程和式(3),可得其本构方程为

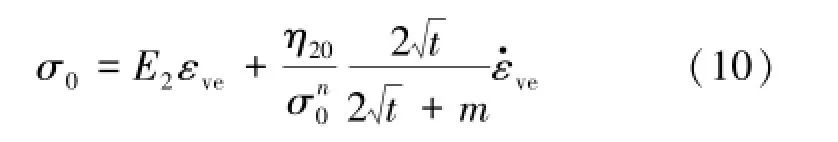
式中,E2为NN/H体黏弹性模量。

将式(10)变形可得

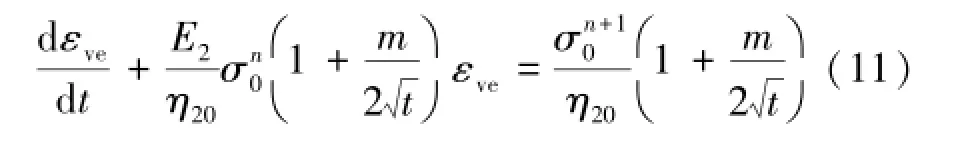
对式(11)解微分方程,并考虑初始条件:t=0, εve=0,可得NN/H体的蠕变方程为

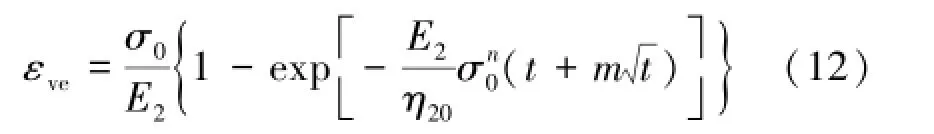
根据式(5),(6),(9),(12)可得MBurgers模型在一维应力状态下的蠕变方程为

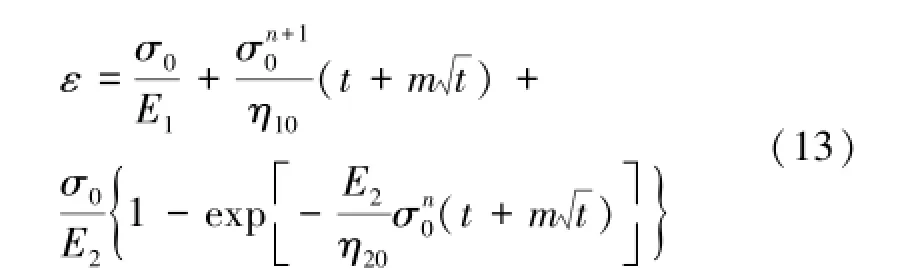
三维应力状态下,盐岩内部应力张量σij可分解为球应力张量σm和偏应力张量Sij,应变张量εij可分解为球应变张量εm和偏应变张量eij,并且在弹性状态下满足

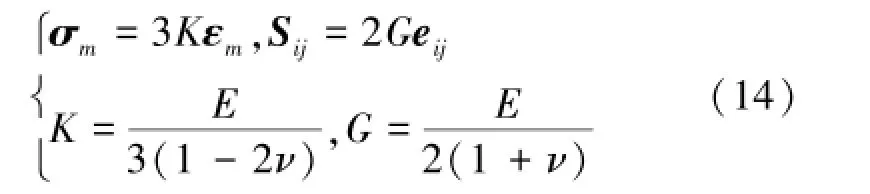
式中,K为体积模量;G为剪切模量;E为弹性模量;ν为泊松比。

为了得到三维形式的蠕变方程,假设[15]:①盐岩蠕变变形仅由应力偏量引起;②盐岩材料各向同性,且其在拉压应力状态下的变形曲线与蠕变曲线相似;③蠕变过程中,盐岩泊松比保持不变。

根据以上假设,三维应力状态下,考虑σ2= σ3,MBurgers模型轴向蠕变方程可表示为

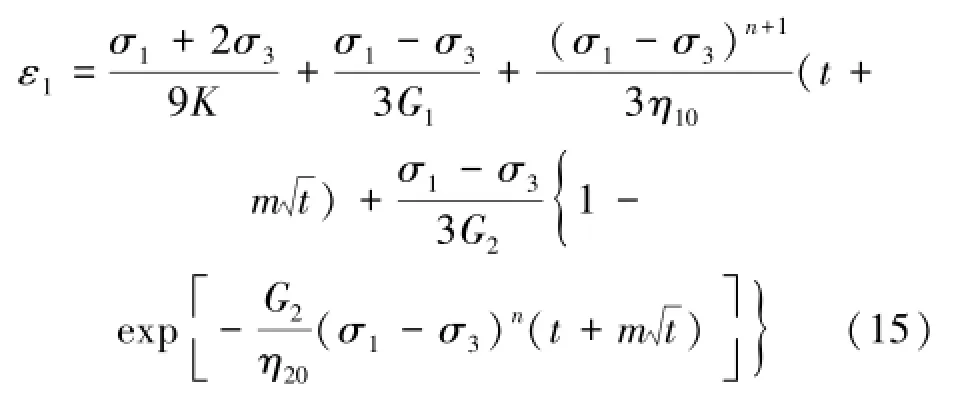
由式(13)和式(15)可以看到,当m=n=0时,MBurgers模型退化为常规Burgers模型;当m=0, n≠0时,MBurgers模型可反映应力水平对盐岩非线性蠕变特性的影响;当m≠0,n=0时,MBurgers模型可反映蠕变时间对盐岩非线性蠕变特性的影响;当m≠0,n≠0时,模型可综合反映应力水平和蠕变时间的影响。

2.3 非线性模型参数敏感性分析

(1)参数m,n的影响。

图4(a)为应力和其余参数均相同,参数m取不同值时,利用式(13)计算得到的MBurgers模型蠕变曲线;图4(b)为应力和其余参数均相同,参数n取不同值时的蠕变曲线。

由图4可以看到:①m越大,相同时刻蠕变变形量和蠕变速率越大,同时,衰减蠕变阶段蠕变曲线曲率半径越大,持续时间越长,进入稳态蠕变越晚,且相同时刻的蠕变变形量随m增大而近似呈线性规律增大;②随着n增大,相同时刻蠕变变形量、蠕变速率及衰减蠕变阶段蠕变曲线曲率半径等也逐渐增大,且蠕变变形量和蠕变速率随n值增大而呈非线性加速增大,这说明MBurgers模型对参数n的敏感性要远高于m。

(2)应力水平的影响。

图5为其余模型参数均相同时,不同应力水平下MBurgers模型的蠕变曲线。其中图5(a)为不考虑应力水平对黏滞系数的影响即n=0时的蠕变曲线,图5(b)为考虑应力水平对黏滞系数的影响即n＞0时的蠕变曲线。

由图5可以看出,当n=0时,虽然蠕变变形量和蠕变速率等均随应力水平提高而逐渐增大,但基本呈线性规律增大;而当n＞0时,蠕变量和蠕变速率随应力水平提高而呈非线性加速增大,这与图1中试验曲线情况较为符合,这也说明了本文考虑应力水平对黏滞系数影响的必要性和合理性。

3 盐岩非线性蠕变模型参数识别

曲线拟合法是确定岩石流变模型参数应用较为

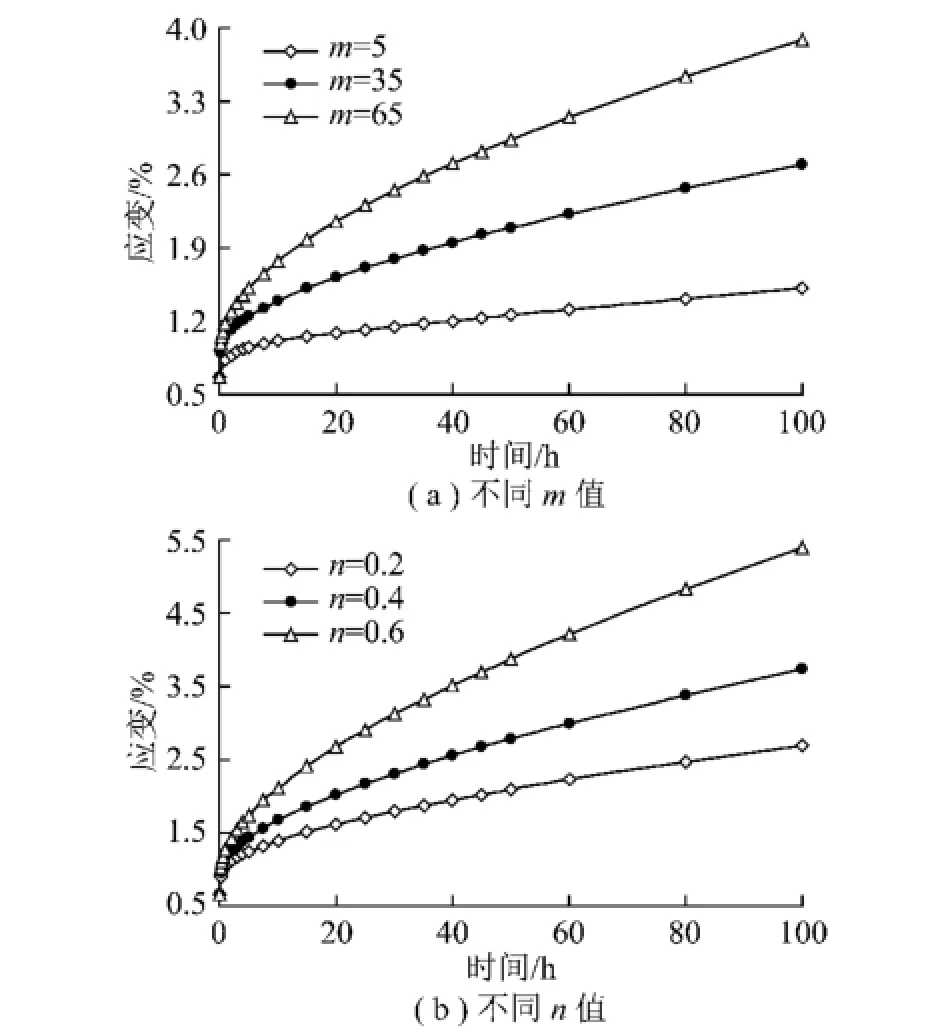
图4 不同参数取值下MBurgers模型蠕变曲线Fig.4 Creep curves of MBurgers model with different parameter values

广泛的一种方法[13]。本文根据盐岩三轴压缩蠕变试验结果,基于最小二乘法基本原理,利用1stOpt优化软件,采用曲线拟合法对MBurgers模型参数进行反演识别。参数反演结果见表1,拟合曲线和试验曲线对比情况如图6所示。

由表1可见,尽管这两个盐岩试件具有一定的离散性,导致拟合得到的参数如黏滞系数、黏弹性模量等具有一定的差别,但表征非线性影响的参数m和n的差别并不大。同时,由图6可以看出,MBurgers模型拟合曲线和试验曲线吻合良好,误差较小,说明该模型可以很好地描述盐岩的黏弹性蠕变特性,具有一定的适用性。

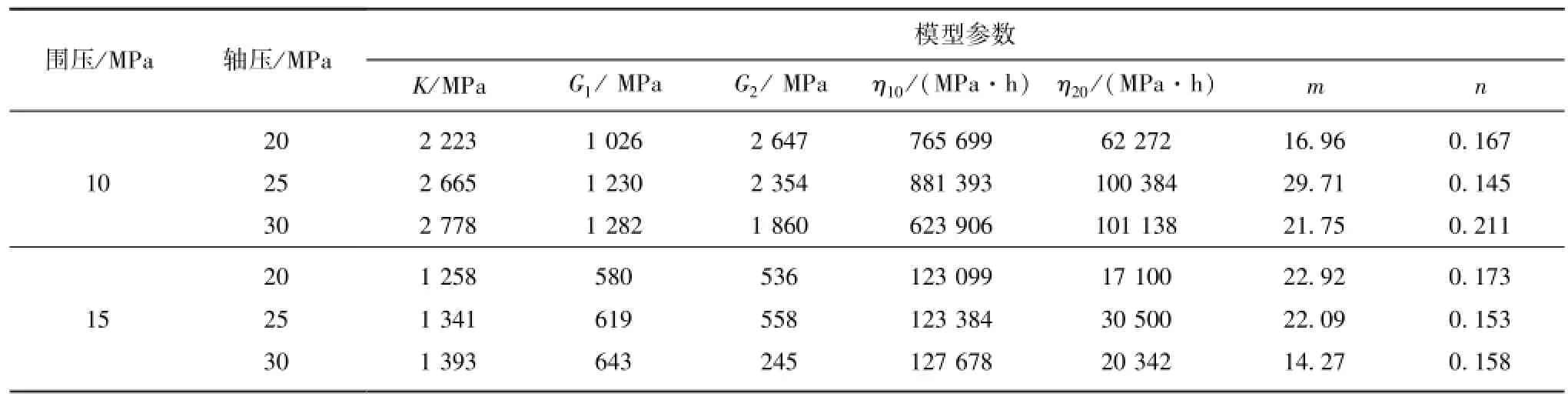
表1 MBurgers模型参数反演结果Table 1 Inversion results of MBurgers model

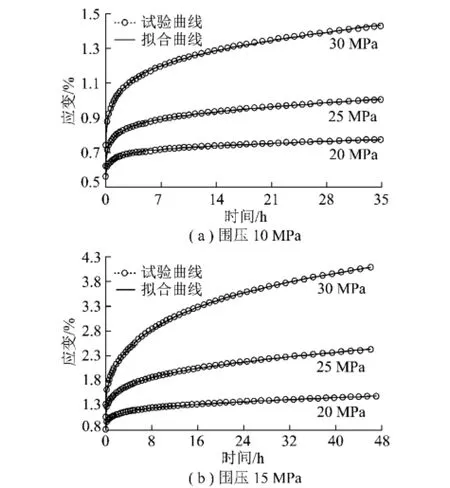
图6 拟合曲线和试验曲线对比Fig.6 Comparison between fitting curves and test curves

4 结 论

(1)盐岩蠕变试验表明,在围压一定的情况下,随着轴向应力增大,盐岩瞬时应变、蠕变应变以及蠕变速率等均随之增大,进入稳态蠕变阶段所需要的时间逐渐延长。

(2)等时应力－应变曲线表明,盐岩蠕变具有非线性特征,且其非线性程度与蠕变时间和应力水平有关,蠕变时间越长、应力水平越高,非线性程度越高。

(3)提出了一种非线性黏滞体,其黏滞系数是所加应力水平和蠕变时间的函数,将非线性黏滞体替换常规Burgers模型中的线性黏滞体,建立了可描述盐岩非线性蠕变特性的MBurgers模型。

(4)根据盐岩蠕变试验结果,采用曲线拟合法对MBurgers模型的参数进行了反演识别。拟合曲线和试验曲线对比显示,两者吻合良好,误差较小,说明该模型可以很好的描述盐岩的蠕变特性。

[1] Asanov V A.Deformation of salt rock joints in time[J].Journal of Mining Science,2004,40:154－169.

[2] 李 萍,邓金根,孙 焱,等.川东气田盐岩、膏盐岩蠕变特性试验研究[J].岩土力学,2012,33(2):444－448.

Li Ping,Deng Jingen,Sun Yan,et al.Experimental study of creep characteristics of rock gypsum-salt and rock salt in Chuandong gas field[J].Rock and Soil Mechanics,2012,33(2):444－448.

[3] 陈 锋,李银平,杨春和,等.云应盐矿盐岩蠕变特性试验研究[J].岩石力学与工程学报,2006,25(S1):3022－3027.

Chen Feng,Li Yinping,Yang Chunhe,et al.experimental study on creep behaviors of rock salt in Yunying salt mine[J].Chinese Journal of Rock Mechanics and Engineering,2006,25(S1):3022－3027.

[4] Chan K S,Brodsky N S,Fossum A F,et al.Damage-induced non-associated inelastic flow in rock salt[J].International Journal of Plasticity,1994,10(6):623－642.

[5] Wang G J.A new constitutive creep-damage model for salt rock and its characteristics[J].International Journal of Rock Mechanic and Mining Science,2004,41(S1):61－67.

[6] 马林建,刘新宇,方 秦,等.联合广义Hoek－Brown屈服准则的盐岩黏弹塑性损伤模型及其工程应用[J].煤炭学报,2012, 37(8):1299－1303.

Ma Linjian,Liu Xinyu,Fang Qin,et al.An elasto-viscoplastic damage model combined with generalized Hoek-Brown failure criterion for rock salt and its engineering application[J].Journal of China Coal Society,2012,37(8):1299－1303.

[7] 杜 超,杨春和,马洪岭,等.深部盐岩蠕变特性研究[J].岩土力学,2012,33(8):2451－2456.

Du Chao,Yang Chunhe,Ma Hongling,et al.Study of creep charac-teristics of deep rock salt[J].Rock and Soil Mechanics,2012, 33(8):2451－2456.

[8] 唐明明,王芝银,丁国生,等.含夹层盐岩蠕变特性试验及其本构关系[J].煤炭学报,2010,35(1):42－45.

Tang Mingming,Wang Zhiyin,Ding Guosheng,et al.Creep property experiment and constitutive relation of salt-mudstone interlayer[J].Journal of China Coal Society,2010,35(1):42－45.

[9] 郤保平,赵阳升,赵延林,等.含高盐份泥岩夹层的盐岩蠕变特性研究[J].地下空间与工程学报,2007,3(1):23－26.

Xi Baoping,Zhao Yangsheng,Zhao Yanlin,et al.Study on creep property of rock salt with mudstone interlayer[J].Chinese Journal of Underground Space and Engineering,2007,3(1):23－26.

[10] 刘 江,杨春和,吴 文,等.盐岩蠕变特性和本构关系研究[J].岩土力学,2006,27(8):1267－1271.

Liu Jiang,Yang Chunhe,Wu Wen,et al.Study on creep characteristics and constitutive relation of rock salt[J].Rock and Soil Mechanics,2006,27(8):1267－1271.

[11] Zhou H W,Wang C P,Han B B,et al.A creep constitutive model for salt rock based on fractional derivatives[J].International Journal of Rock Mechanics and Mining Sciences,2011,48(1):116－121.

[12] 薛凯喜,赵宝云,刘东燕,等.岩石非线性拉、压蠕变模型及其参数识别[J].煤炭学报,2011,36(9):1440－1445.

Xue Kaixi,Zhao Baoyun,Liu Dongyan,et al.Nonlinear creep model of rock in tensile or compressive stress and its parameter identification[J].Journal of China Coal Society,2011,36(9):1440－1445.

[13] 蒋昱州,张明鸣,李良权.岩石非线性黏弹塑性蠕变模型研究及其参数识别[J].岩石力学与工程学报,2008,27(4):832－839.

Jiang Yuzhou,Zhang Mingming,Li Liangquan.Study on nonlinear viscoelasto-plastic creep model of rock and its parameter identification[J].Chinese Journal of Rock Mechanics and Engineering, 2008,27(4):832－839.

[14] 高赛红,曹 平,汪胜莲,等.改进的岩石非线性黏弹塑性蠕变模型及其硬化黏滞系数修正[J].煤炭学报,2012,37(6):936－943.

Gao Saihong,Cao Ping,Wang Shenglian,et al.Improved nonlinear viscoelasto-plastic rheological model of rock and its correction of hardening coefficient of viscosity[J].Journal of China Coal Society,2012,37(6):936－943.

[15] 赵延林,曹 平,文有道,等.岩石弹黏塑性流变试验和非线性流变模型研究[J].岩石力学与工程学报,2008,27(3):477－486.

Zhao Yanlin,Cao Ping,Wen Youdao,et al.Elastovisco-plastic rheological experiment and nonlinear rheological model of rocks [J].Chinese Journal of Rock Mechanics and Engineering,2008, 27(3):477－486.

[16] 周长冰,万志军,张 源,等.高温三轴应力下气煤蠕变特征及本构模型[J].煤炭学报,2012,37(12):2020－2025.

Zhou Changbing,Wan Zhijun,Zhang Yuan,et al.Creep characteristics and constitutive model of gas coal mass under high temperature and triaxial stress[J].Journal of China Coal Society,2012, 37(12):2020－2025.

[17] 陈文玲,赵法锁,弓虎军.三轴蠕变试验中云母石英片岩蠕变参数的研究[J].岩石力学与工程学报,2011,30(S1):2810－2816.

Chen Wenling,Zhao Fasuo,Gong Hujun.study of creep parameters of mica-quartzoseschist during triaxial creep test[J].Chinese Journal of Rock Mechanics and Engineering,2011,30(S1):2810－2816.

Creep properties of salt rock and its nonlinear constitutive model

WANG Jun-bao1,2,LIU Xin-rong1,2,GUO Jian-qiang2,HUANG Ming3

(1.College of Civil Engineering,Xi’an University of Architecture and Technology,Xi’an 710055,China;2.College of Civil Engineering,Chongqing University,Chongqing 400045,China;3.College of Civil Engineering,Fuzhou University,Fuzhou 350108,China)

In order to study the creep property of salt rock,triaxial compression creep tests with step loading axial stress to salt rock specimens were carried out on the RLW－2000 rock rheology testing machine.The test results show that the instantaneous strain,creep strain and creep velocity of salt rock increase gradually with the increasing of axial stress,meanwhile,the duration of the primary creep stage gradually extend.And isochronous stress-strain curves of salt rock indicate that the creep process of salt rock has nonlinear characteristic,and the nonlinear degree is related to creep time and stress level.Based on nonlinear rheological theory,a new nonlinear viscosity component with a variable viscosity coefficient was proposed,and the viscosity coefficient of which was time and stress-dependent.Then,by using this proposed nonlinear component to replace the conventional viscous components in Burgers model,a nonlinear viscoelasticity creep model,which was named MBurgers model and can describe the nonlinear creep property of salt rock was established.According to triaxial compression creep test results of salt rock,the parameters of MBurgers model were inversed by using curve fitting method.And the theoretical curves accord well with the test curves,which indicates that the MBurgers model can describe the creep property of salt rock.

TD313;TU45

A

0253－9993(2014)03－0445－07

王军保,刘新荣,郭建强,等.盐岩蠕变特性及其非线性本构模型[J].煤炭学报,2014,39(3):445－451.

10.13225/j.cnki.jccs.2013.0383

Wang Junbao,Liu Xinrong,Guo Jianqiang,et al.Creep properties of salt rock and its nonlinear constitutive model[J].Journal of China Coal Society,2014,39(3):445－451.doi:10.13225/j.cnki.jccs.2013.0383

2013－03－27 责任编辑:许书阁

国家重点基础研究发展计划(973)资助项目(2009CB724606);国家自然科学基金资助项目(41202195)

王军保(1982—),男,河北石家庄人,讲师,博士。Tel:029－65653814,E－mail:xajdwangjunbao@163.com