空间的再生核及不等式
2014-06-05倪金霞
倪金霞
(南京交通职业技术学院基础教学部,江苏 南京 211188)
倪金霞
(南京交通职业技术学院基础教学部,江苏 南京 211188)
利用再生核空间和傅立叶变换的性质,构造了W12(R)空间的再生核,讨论了该再生核与微分方程的关系,并给出了W12(R)空间的几个不等式。
再生核;傅立叶变换;不等式
再生核空间是一类基于Hilbert空间框架下的函数空间,再生核空间的核函数具有再生性质。再生核理论已广泛应用于数值分析、微分方程求解、数据统计分析以及模式识别等领域。文献[1]将再生核用于数值分析,给出了插值问题的最佳数值原函数。文献[2-3]基于再生核空间,研究了微分算子插值样条及最佳插值逼近算子,给出了微分算子样条插值函数,文献[4]利用再生核证得了高阶微分算子插值样条及空间中最佳插值逼近算子的一致性。文献[5]基于再生核空间并利用再生核技巧,用于求解一类变系数的偏微分方程。文献[6]在再生核空间中,利用升元的方法将一类非线性常微分方程转化为二维线性算子方程,然后通过构造零空间的一组标准正交基,以获得线性算子方程的所有解的表达形式。文献[7]则讨论了波动方程的解与再生核空间的关系,进而得到了波动方程的解的反演公式及等距恒等式。文献[8]利用再生核理论对数据进行统计分析。文献[9]则将再生核理论应用到模式识别领域,发展了著名的核主成分分析方法,文献[10]则利用再生核方法将经典的线性鉴别分析方法发展为核线性鉴别分析方法,用于图像特征提取。如今,基于再生核空间的模式识别特征提取方法已在人脸识别、虹膜识别、指纹识别等实际应用领域取得了成功。再生核理论的这些应用,彰显了其作为数学基础理论的重要性以及应用范围的广泛性。
1 再生核希尔伯特空间及其性质
定义1[14]设H是Hilbert函数空间,其元素是某个抽象集合E上的实值或复值函数,若对任何y∈E,E×E上的二元函数K(x,y)满足:
1)K(x,y)作为x的函数是H中的元素;
2)对任何u∈H有u(y)=<u(x),K(x,y)>
则称K(x,y)是Hilbert函数空间H的再生核,并称H是再生核空间。
性质1 如果Hilbert函数空间H存在再生核K(x,y),则该再生核是唯一的。
性质2 假设K(x,y)是Hilbert函数空间H的再生核,则K(x,y)=K(y,x)。
性质3 Hilbert函数空间H存在再生核K(x,y)的充分必要条件是:对于任一y∈E,u(y)都是H上的连续线性泛函,即存在常数C≥0,使得


引理1[15]对于任意都有
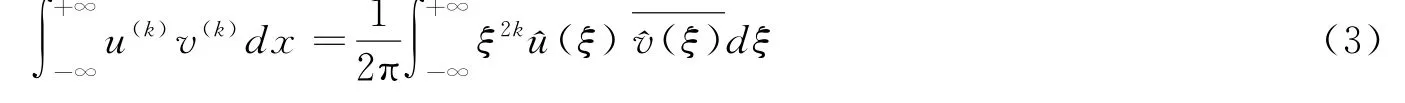
其中,k=0或1。
引理2[15]如果u,^u∈L1(R),则
下面证明定理1。
证明:
令


下面计算p(x)。对于方程z2+1=0取其位于上半平面的根z1=i,以复平面上半圆的边界{|z|≤R,Im(z)≥0}作为积分路径CR进行积分,当x>0时,令R→∞,有

根据留数定理,可以得到

当x<0时,由p(x)=p(-x),有

综合(7)、(8)两式,可以将p(x)进一步表示为

进一步地,令
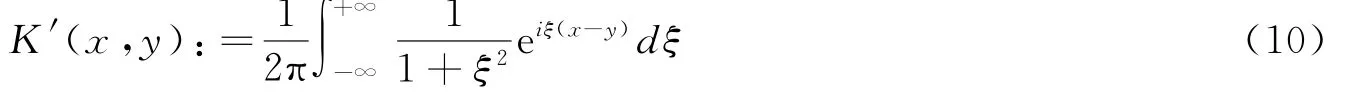
根据式(5),可以得

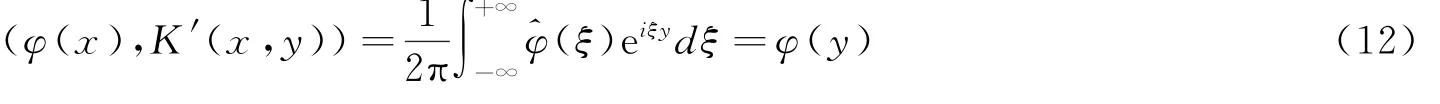
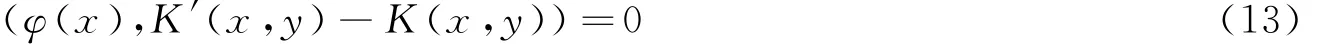


易得
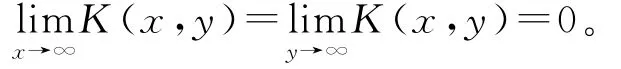
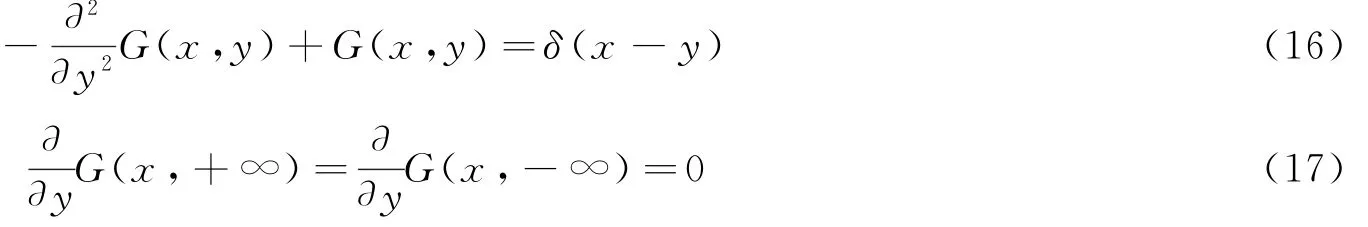
对任意指定的x∈R,当x≠y时,(16)的特征方程为λ2-1=0,其特征根λ1=1,λ2=-1。所以G (x,y)有表示式
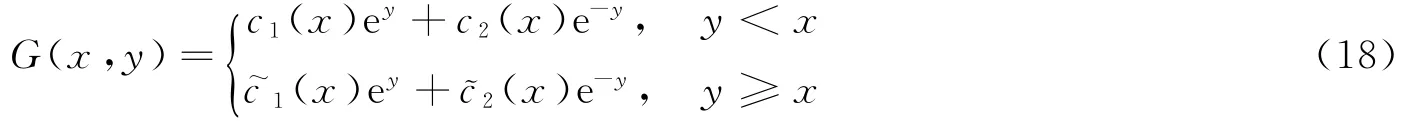
(16)式表明,G(x,y)在x点连续,所以:
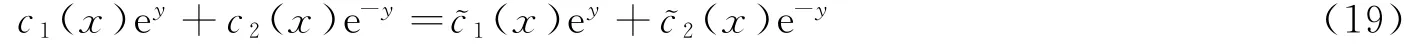
又由(16)式,∀ε>0,有
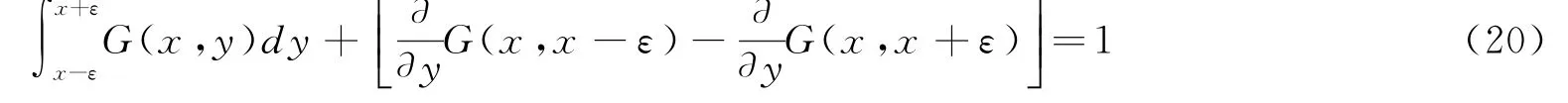
因G(x,y)在x点连续,所以在(20)式中令ε→0,则有
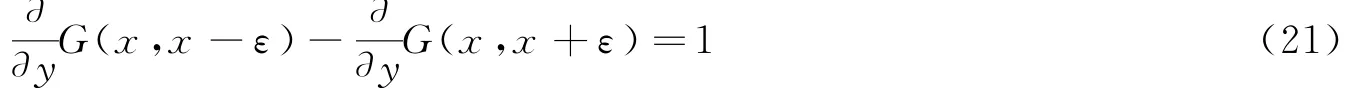
所以由(18)式得
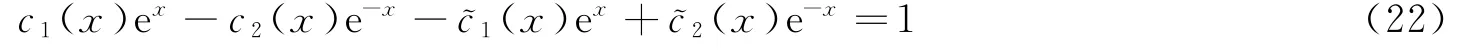
所以

事实上,由
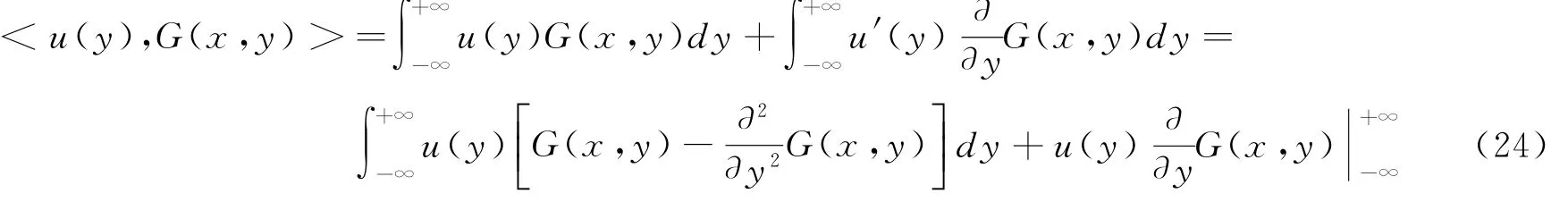
以及(16)、(17)式,可得
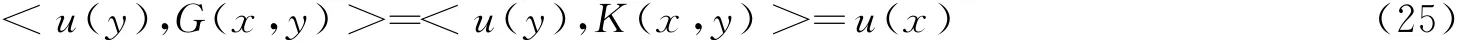
4 再生核空间的若干不等式
4.1 Sobolev不等式
Sobolev不等式又称Sobolev嵌入不等式,在偏微分方程的研究中具有基础性的作用。本文考虑如下形式的Sobolev嵌入不等式


其中最佳常数c1为

且当u具有C·u(x)的形式时,(27)式中的等号成立,其中:

其中y是R中的一任意点。
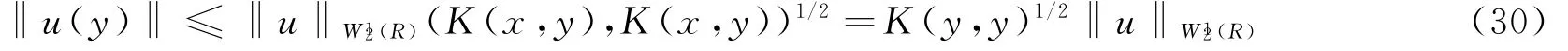
因此,有
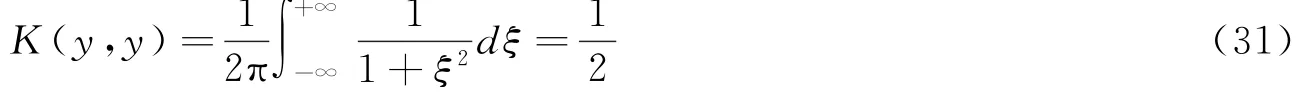
4.2 赋范及卷积不等式
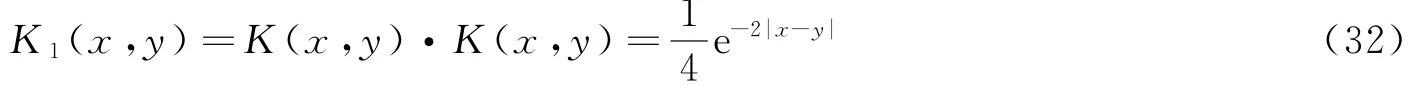
则有
显然,K1(x,y)在R上是正定的,因此,存在一个希尔伯特空间W1(R),其再生核为K1(x,y),类似于空间,再生核希尔伯特空间W1(R)上的范数为
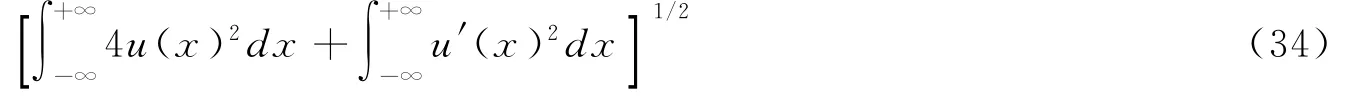
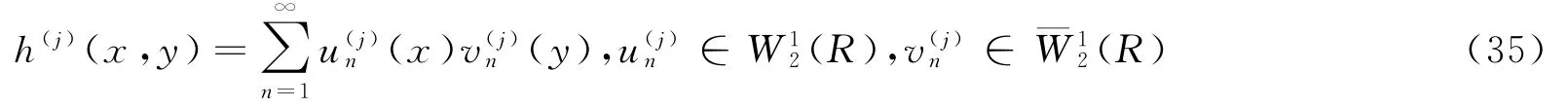
并具有范数
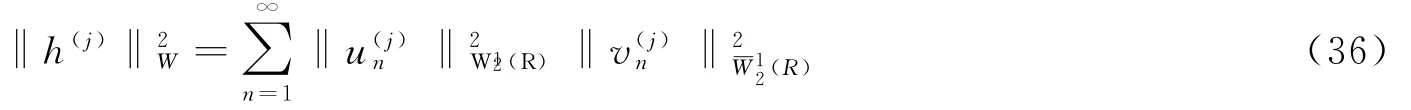
内积
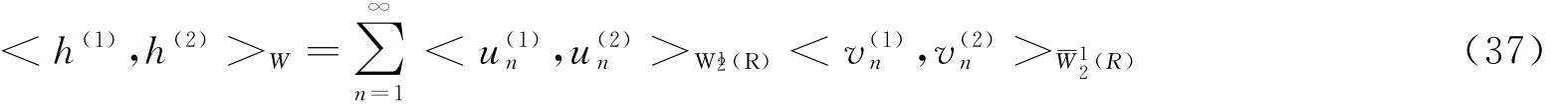
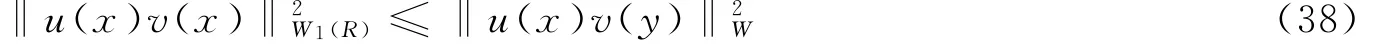
根据公式(38),可以得到下面的定理。
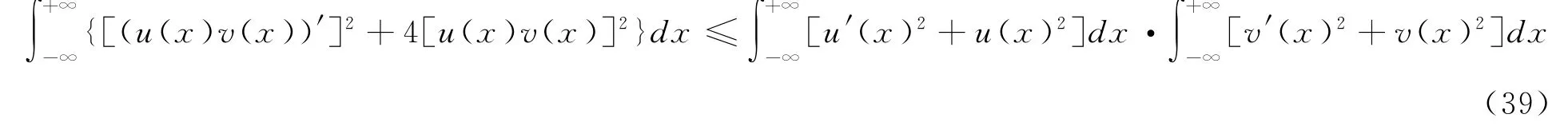

及其等距恒等式
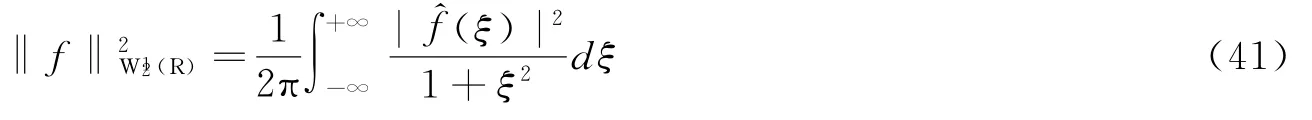

及其等距恒等式
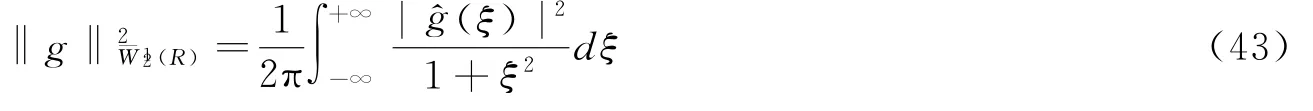
由(40)、(42)式,可得
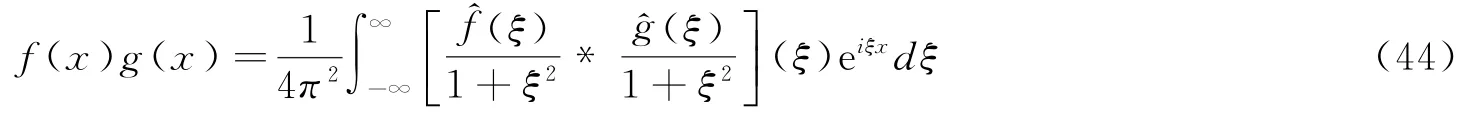
对于公式(33),可以得到类似的等距恒等式
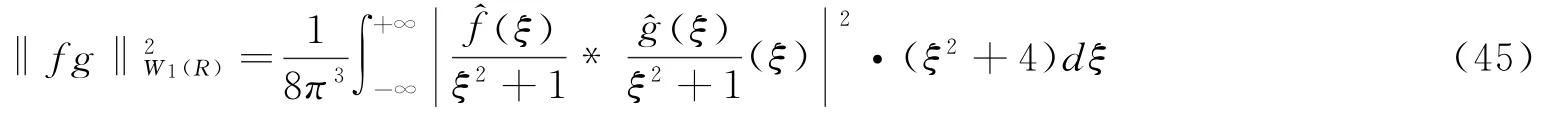
根据定理3,由公式(38)、(41)、(43)及(45),可以得到基于频域卷积形式的不等式。

5 结 论
本文利用再生核理论和傅立叶分析理论的基本性质及定理,从新的角度讨论了W12(R)空间中的再生核的构造,建立了再生核与微分方程的联系,给出了基于该空间的几个不等式,进一步丰富了再生核的生成方式,拓宽了再生核理论的应用范围。
[2]邓彩霞,邓中兴.再生核空间中样条插值算子与最佳插值逼近算子的一致性[J].高等学校计算数学学报,1995,17(2): 119-128
[5]王玉兰,朝鲁.利用再生核解一类变系数偏微分方程[J].应用数学和力学,2008,29(1):118-126
[6]杜红.求解一类非线性常微分方程的方法[J].淮北煤炭师范学院学报:自然科学版,2007,28(2):16-19
[7]邢佳,邓彩霞,倪金霞.波动方程的解与再生核空间的关系[J].数学的实践与认识,2008,38(6):203-206
[8]Alain Berlinet,Christine Thomas-Agnan.Reproducing Kernel Hilbert Spaces in Probability and Statistics[M].[S.l.]: Kluwer Academic,2004
[9]B.Schölkopf,A.Smola,and K.R.Müller.Nonlinear Component Analysis as a Kernel Eigenvalue Problem[J].Neural Computation,1998,10(5):1299-1319
[10]Belhumeur V,Hespanha J,Kriegman D.Eigenfaces vs Fisherfaces:Recognition Using Class Specific Linear Projection [J].IEEE Trans on Pattern Analysis and Machine Intelligence,1997,19(7):711-720
[11]李云晖,崔明根.再生核空间中的一个数值泛函极值问题[J].黑龙江大学自然科学学报,2002,19(1):18-20
[14]Aronszajn N.Theory of reproducing Kernels[J].Transactions of the American Mathematical Society,1950,68(3): 337-404
[15]潘文杰.傅立叶分析及其应用[M].北京:北京大学出版社,2000
(责任编辑:马金玉)
Reproducing Kernel and Inequalities in(R)Space
NI Jin-xia
(Nanjing Communications Institute of Technology,Nanjing 211188,China)
The reproducing kernel in the W12(R)space is constructed by virtue of the properties of reproducing space and Fourier transform,and the relation between this function and differential equation is discussed.Several inequalities in W12(R)space are given.
reproducing kernel;Fourier transform;inequality
O178
A
1672-755X(2014)03-0005-06
2014-07-02
2014年度南京交通职业技术学院青年科研基金重点项目
倪金霞(1979-),女,甘肃定西人,讲师,硕士,主要从事再生核、小波分析及其应用研究。
