高阶欧拉多项式与交错等幂和多项式的对称等式

伍 鸣

(金陵科技学院公共基础课部,江苏 南京 211169)

高阶欧拉多项式与交错等幂和多项式的对称等式

伍 鸣

(金陵科技学院公共基础课部,江苏 南京 211169)

推广了一个关于欧拉数与交错等幂和多项式的对称关系式,获得了包含多个高阶欧拉多项式和交错等幂和多项式的对称等式。

欧拉数;欧拉多项式;高阶欧拉多项式;交错等幂和多项式

欧拉数En是组合数学中一类非常重要的数列,在正割secx和双曲正割sechx的泰勒级数中出现。它由指数生成函数

所定义,奇数项的欧拉数皆为0,偶数项的欧拉数正负相间,分别为:

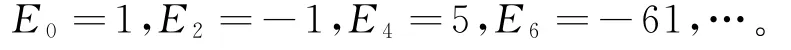
与此同时,欧拉多项式En(x)也类似地由指数生成函数

1 欧拉数的基本对称等式

Tuenter[4]曾发现一个关于伯努利数与等幂和多项式的对称关系式。Liu和Wang[5]在此研究成果上证明了一个关于欧拉数与交错等幂和多项式的对称关系式,如下:

引理1 对任意正整数a,b,m以及n≥0,如果a与b具有相同奇偶性,那么有

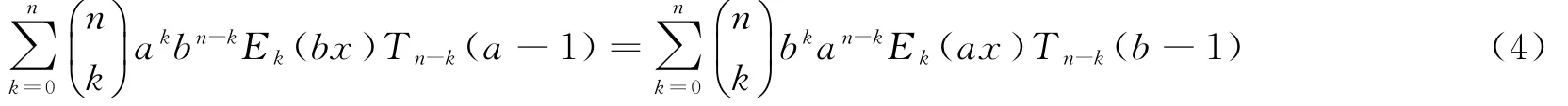
Yang[6]证明了一个高阶伯努利多项式与等幂和多项式的对称关系式,Liu和Wang[5]类似地证明了高阶欧拉多项式与交错等幂和多项式的对称关系,如下:

在数学课堂上进行对学生自主学习能力的培养，需要积极进行对课堂情境的创设，结合学生的学习兴趣和爱好，进行对各种数学知识的有效教学，激发学生的学习热情，引导学生进行自主学习，提高教学的效率。在教学中教师需要根据教材内容的需要进行对课堂的创设，结合学生日常生活中的各种事物或常识，进行对学生的教学引导，推动与鼓励学生进行各种自主探究活动，激发学生的学习兴趣，提高数学课堂的教学质量，实现对学生自主学习能力的培养。

引理2 对任意正整数a,b,m以及n≥0,如果a与b具有相同奇偶性,那么有

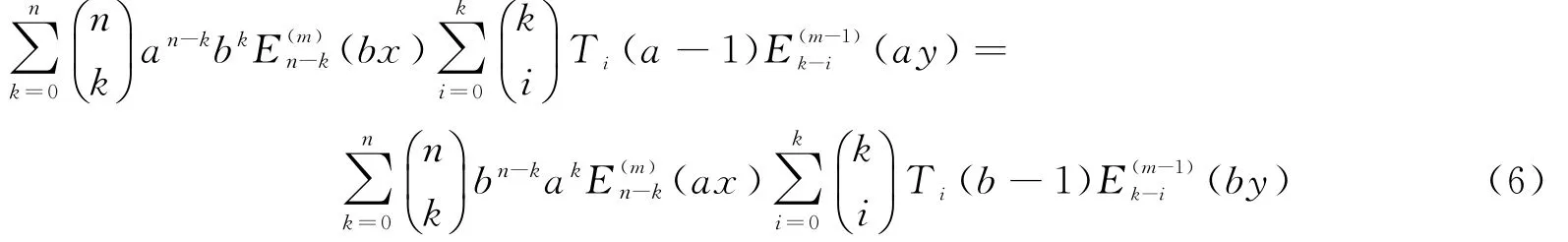
2 含交错幂和多项式的欧拉多项式对称式

定理1 对任意正整数m,ai(i=1,2,…,k)以及n≥0,当1≤p＜q≤k时,如果ap与aq具有相同奇偶性,那么有

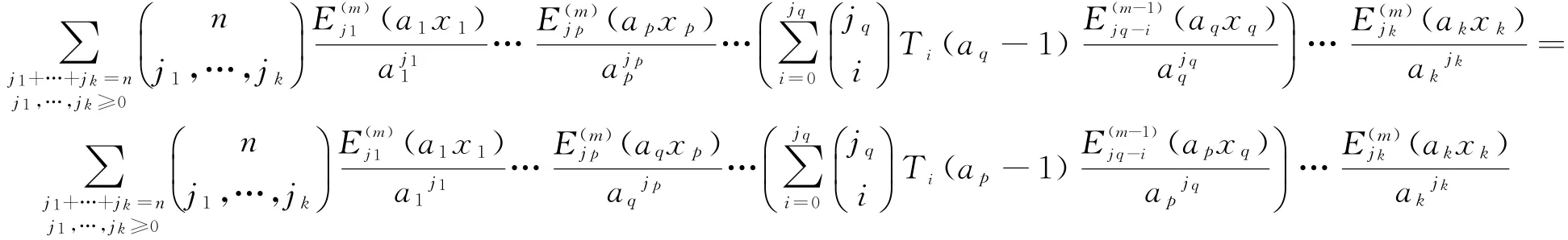
证明 假设ap与aq都是偶数,可设函数

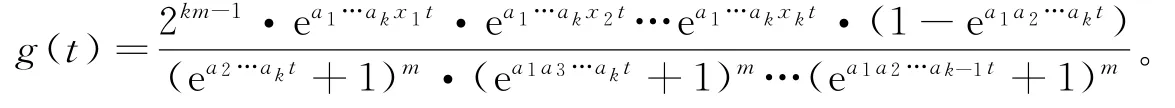
观察到这个函数的表达式是关于ai(i=1,2,…,k)完全对称的,接下来用不同方式将g(t)展开成无穷级数:

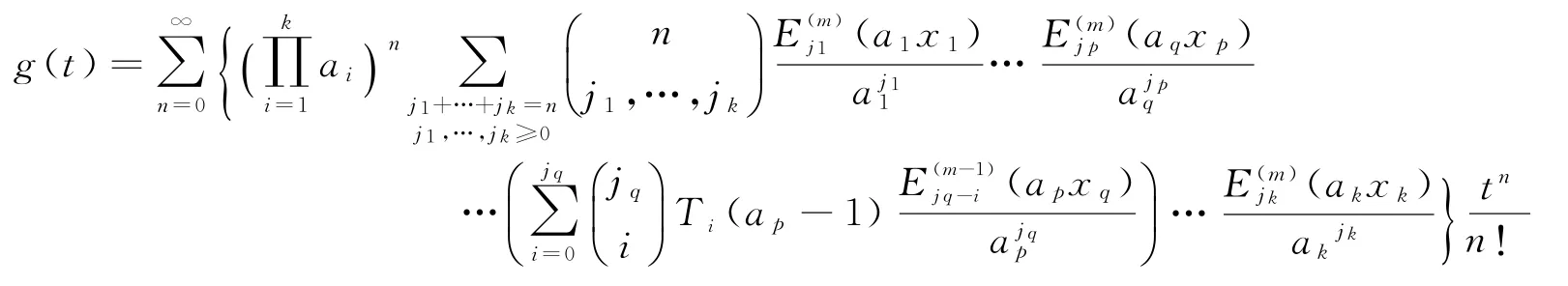
通过对比这两个展开式中的系数,容易得出结果。

假设ap与aq都是奇数,可设函数

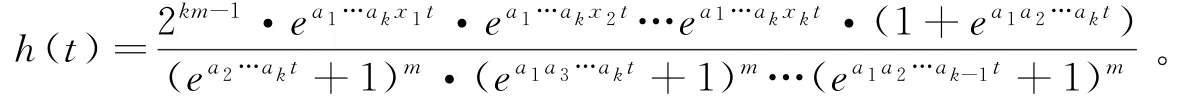
运用同样的方法,可以得出结果。证毕。

在定理1中,如果让k=2,就可以得到引理2中的等式(6)。

推论1 对任意正整数ai(i=1,2,…,k),以及n≥0,当1≤p＜q≤k时,如果ap与aq具有相同奇偶性,那么有

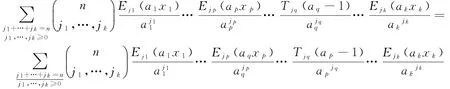
证明 在定理1中,让m=1,xq=0,即得。证毕。

特别地,在推论1中,如果让k=2,就可以得到引理1中的等式(4)。

定理2 对任意正整数m,ai(i=1,2,…,k),n≥0,当1≤p＜q≤k时,如果ap与aq具有相同奇偶性,那么有

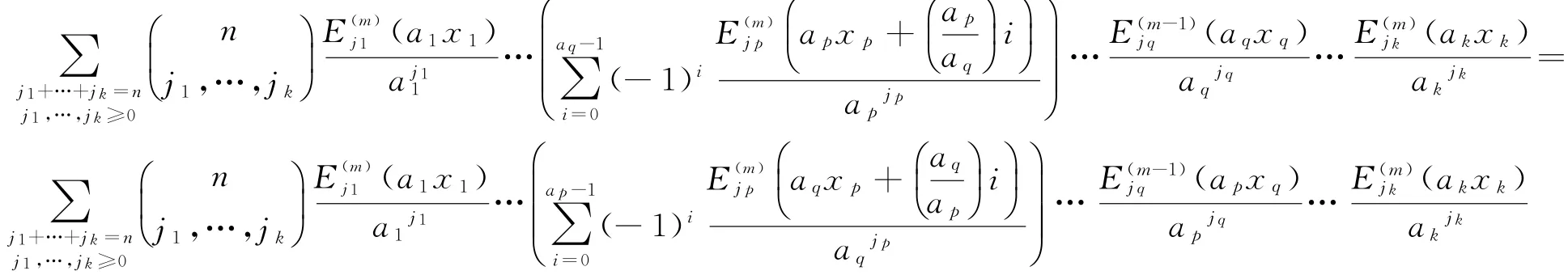
证明 假设ap与aq都是偶数,可设函数一方面,

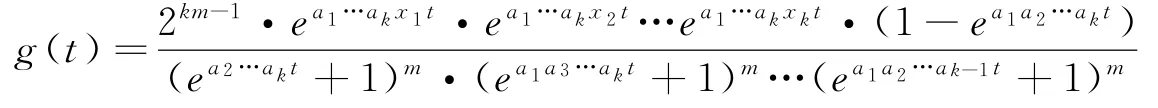
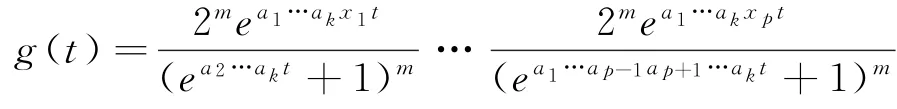
另一方面,同样可得

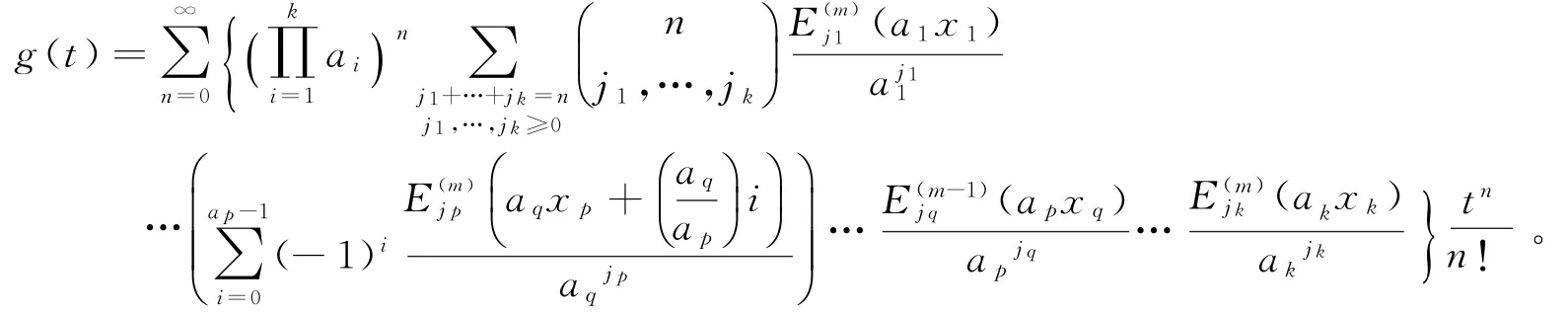
假设ap与aq都是奇数,可设函数

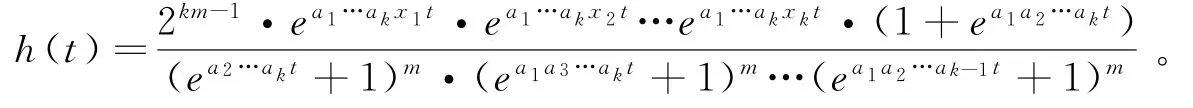
运用同样的方法,可以得出结果。证毕。

3 结 语

本文在Liu和Wang工作的基础上,推广了一个关于欧拉数与交错等幂和多项式的对称关系式,获得了关于多个高阶欧拉多项式与交错等幂和多项式的对称等式,它将已有的研究结果都包含在这一等式中,并且得到了欧拉多项式乘法定理的推广形式。

[1]Dilcher K.Sums of Products of Bernoulli numbers[J].Journal of Number Theory,1996,60:23-41

[2]Satoh J.Sums of Products of Two q-Bernoulli Numbers[J].Journal of Number Theory,1999,74:173-180

[3]Wu M,Pan H.Sums of Products of Bernoulli Numbers of the Second Kind[J].The Fibonacci Quarterly,2007,45:146 -150

[4]Tuenter H J H.A Symmetry of Power Sum Polynomials and Bernoulli Numbers[J].The American Mathematical Monthly,2001,108:258-261

[5]Liu H,Wang W.Some Identities on the Bernoulli,Euler and Genocchi Polynomials via Power Sums and Alternate Power Sums[J].Discrete Mathematics,2009,309(10):3346-3363

[6]Yang S L.An Identity of Symmetry for the Bernoulli polynomials[J].Discrete Mathematics,2008,308:550-554

(责任编辑:马金玉)

An Identity of Symmetry for Higher Order Euler Polynomials and Alternate Power Sum Polynomials

WU Ming
(Jingling Institute of Technology,Nanjing 211169,China)

A relation of symmetry between Euler polynomials and alternate power sum polynomials is generalized.An identity of symmetry for several higher order Euler polynomials and alternate power sum polynomials is obtained.

Euler number;Euler polynomial;higher order Euler polynomials;alternate power sum polynomials

O157.1

A

1672-755X(2014)03-0001-04

2014-08-28

伍鸣(1978-),女,江苏南京人,讲师,硕士,主要从事组合、数论等方面的研究。