三点弯曲式钻杆矫直力学模型建立与分析

高 凯

（中石化胜利石油工程有限公司钻井工艺研究院，山东东营257017）①

三点弯曲式钻杆矫直力学模型建立与分析

高 凯

（中石化胜利石油工程有限公司钻井工艺研究院，山东东营257017）①

为了分析钻杆在三点弯曲矫直过程的受力及变形，基于金属弹塑性变形理论，研究钻杆在弯曲过程中的弯矩、曲率以及挠度之间的关系，建立钻杆压力矫直力学模型，并采用A N S Y S软件进行应力、应变、挠度分析。研究表明，该力学模型可定量分析钻杆在矫直过程中的压力、几何尺寸变化关系，提高矫直精度，并对进一步设计自动化钻杆矫直机提供理论指导。

钻杆；矫直；力学模型；弹塑性变形

目前，石油行业中所使用的钻杆经常会发生各种形式的弯曲。在运输、装卸过程中，钻杆弯曲、受扭的现象更是经常发生。如果对弯曲变形的钻杆不及时进行修复，则很难在下一次钻井过程中得到质量优良的井身，并且钻井效率也会大幅降低［1］。油田现场存有大量待修复的钻杆，目前采用三点弯曲矫直机，主要依靠操作人员的经验来控制压块的下压力、行程，实现钻杆矫直。这种工艺使得钻杆矫直精度低，质量波动较大，大量钻杆浪费，钻井成本提高［2-5］。为解决这一问题，本文通过分析钻杆矫直的工艺工程，明确受力状况，并基于金属的弹塑性变形理论建立了钻杆矫直力学模型。由于钻杆初始变形量的不同，下压力及下压行程也不同。随着矫直压力的不断增加，钻杆的变形呈现非线性变化趋势，并且矫直压力随着支点距离的增大而减小，随着压头的下压量、钻杆的截面尺寸以及钻杆材料的屈服极限的增加而增加。该力学模型定量地阐述了钻杆矫直过程各参数之间的关系，对实际工作过程具有一定的理论指导意义。

1 钻杆的三点弯曲矫直原理

在钻杆的矫直过程中，钻杆的弯曲既有弹性弯曲又有部分塑性弯曲。当外界载荷不超过弹性极限时，卸除载荷后，变形可以自行消失；当载荷超过弹性极限并发生塑性变形时，卸除载荷后变形无法消失从而残留下来。

1.1 基本假设

金属材料的弯曲变形在没有到达屈服极限时，纵向纤维的变形遵守虎克定律，应变和应力遵循线性关系：σ＝Eε，（式中：E为弹性摸量，σ为应力，ε为应变）。当材料继续发生弯曲变形，并且达到屈服极限后，材料的弹性性质则有显著的减弱的趋势，应变与应力的关系表现为遵循特定的曲线，在卸载之后应力应变的关系遵循增量虎克定律，即Δσ＝E Δε的增量线性关系，（式中：Δσ为应力增量，Δε为应变增量），而且有一部分变形成为永久变形［6］。金属进入塑性变形阶段后，应力应变关系不再是常数关系，为了分析和计算上的方便，将无屈服平台和小屈服平台的金属归纳为线性强化材料，在一般的压力矫直状态下，其变形量很难超过平台区，作为理想弹塑性材料来处理。

钻杆在矫直压力的作用下虽然存在较为复杂的变化过程，但是在力学模型的推导过程中为了便于理论分析，对钻杆的变形过程做4个假设［7］：

1） 中性轴 忽略弯曲变形引起的中性轴的偏移，即整个矫直过程中性轴保持不变。

2） 管材连续性 管材内部均由连续介质组成，整个钻杆材料内不存在任何空隙，保证钻杆各个参数量均为连续变化的。

3） 管材均匀性 钻杆各处材料性质、组织成分都相同，保证整根钻杆的物理性能一致。

4） 钻杆变形过程 在加压矫直的过程中，钻杆首先开始的是弹性变形，此过程遵循胡克定律，然后部分材料开始发生弹塑性变形。随着压力的持续，钻杆进入弹塑性变形的区域越来越大，如果在某一时刻进行卸载，杆体将会发生部分的弹性回弹，此过程同样遵循胡克定律。

1.2 受力分析

钻杆矫直工作原理如图1所示。

工作时压头对准钻杆弯曲的高峰点，然后开始下压，随着压力的增大，高峰点被压下并产生反向变形，反向变形量的大小以及所需施加的矫直压力的大小均由钻杆的初始弯曲量决定。加压过程中，钻杆受到工作主缸活塞杆压头的压力作用，杆身受到两端支座的支撑作用，并且支座上会有相应的夹紧装置夹住钻杆杆身，以防止其发生转动，从而保证加压矫直时钻杆的稳定性。设作用在钻杆上的总压力为F，两支点对钻杆的支撑力分别为F1和F2，支座与钻杆间摩擦力产生的摩擦阻力矩为M，钻杆受力简图如图2所示。

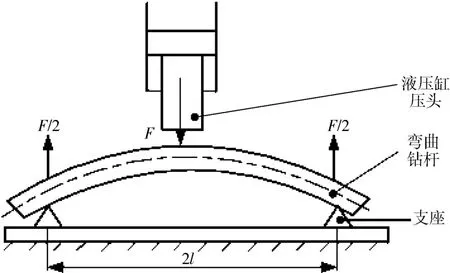
图1 三点弯曲式压力矫直机的工作原理

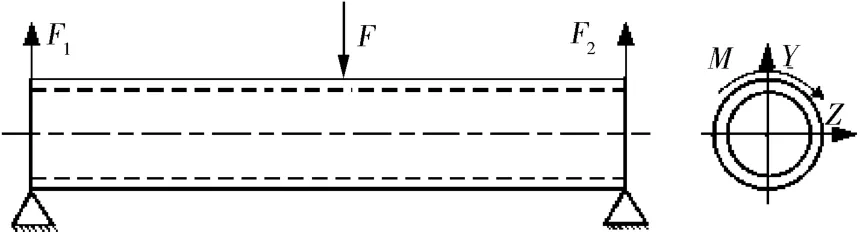
图2 钻杆受力示意

根据空间一般力系的平衡条件，列y方向的力平衡方程：

式中：F为总压力；F1、F2为支点的支反力。

由于两支点在压点两端对称分布，所以F1＝F2。

根据空间一般力系的平衡条件列力矩的平衡方程：

式中：Ff1和Ff2为钻杆与支座间的摩擦力，N；d为钻杆的外径，m；△δ为钻杆弯曲最高点实测位置与理想位置偏移量。

由F1＝F2可以得到：

式中：μ为钻杆与支座间的摩擦因数。

实际工作中△δ值非常小，所以在计算时可以忽略摩擦力产生的影响，即钻杆在矫直过程中只受到中间压力与两支座支撑力的作用。

2 钻杆矫直力学模型建立

钻杆在外力作用下弯曲时，弯曲变形区的外侧材料受到切向拉伸而伸长，内侧材料受到切向压缩而缩短，整个过程是一个复杂的变形过程［8］。分析钻杆整个变形过程时建立相应力学模型，对于分析钻杆矫直变形规律有十分重要的意义。

2.1 压力与变形的关系

压力矫直变形F-δ曲线可用来反映整个压弯修复过程中矫直压力F与矫直挠度δ之间的关系，如图3所示，其变形过程可以分为3段：弹性弯曲O A段、弹塑性弯曲A C段以及卸载后的弹性回弹C D段。

加载后O A段为完全弹性变形阶段，满足线性变化规律；继续施压到C点后停止，A C段为是弹塑性变形阶段，钻杆的变形规律是非线性的；C D段为停止加压后的弹性回弹阶段，回弹部分的变形可以看作是纯弹性变形过程，线性变化规律与O A段相同。钻杆在加压矫直的过程中必须产生过弯现象，产生不可恢复的永久性变形，即残余挠度，导致钻杆的回弹曲线最终只能恢复到D点，O D段所对应的δ0值就是单次矫直过程中产生的残余挠度值。

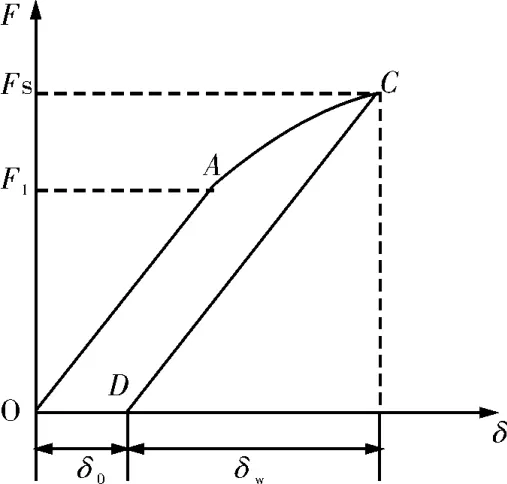
图3 压力矫直过程变形曲线

设由C点到D点产生的弹性回弹量定义为δW，根据F-δ曲线可以推出：对于初始变形量为δ0的钻杆，当下压量为δ∑＝δ0＋δW时，钻杆所对应的矫直过弯量也是δW，即回弹量等于过弯量，如果在此时撤去矫直压力，则钻杆在理论上可以恰好被矫直［9］。因此，如果能够推导出O A段、A C段和C D段的F-δ关系式，就可以根据钻杆的初始弯曲量δ0来计算相应的矫直行程δ∑以及相应的矫直压力F，从而建立整个矫直过程的力学模型。

基于钻杆矫直原理，O A段为钻杆的弹性变形过程，其关系曲线满足胡克定律的线性变化关系：

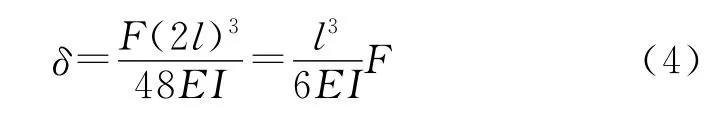
式中：E为钻杆弹性模量，Pa；I为钻杆惯性矩，m4；l为工作过程中支点到压点的距离，m。

钻杆停止加压后的回弹阶段也遵循胡克定律［10］，并且C D段与O A段的斜率是一样的。在A C段过程中由于变形关系较为复杂，所以先为其曲线关系构造某一函数表达式，定义为：

式中：δ为钻杆的挠度。

根据钻杆的初始变形量δ0，可以推导出卸载后C D段所对应的函数关系式为：

式中：k为图3中C D段斜率。

联立式（5）及式（6）可以得出C处的挠度关系式：

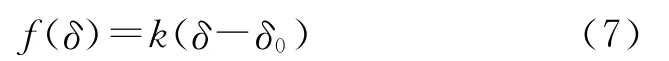
所以整个矫直过程中3个阶段的力学模型（F -δ关系）可以用如下关系式表示：

根据图3，若已知钻杆的初始变形量δ0，就能够以此确定D点的位置，然后通过D点做出弹性回弹线，回弹线将与A C段曲线相交于C点，由此又可以确定C点的位置，进而得出相应的弹性回弹量δW。此时C处所对应的压力就是本次矫直过程中所应提供的最大矫直压力，对应的变形量δ0＋δW就是矫直过程所要提供的最大下压量。

2.2 力学模型

利用式（8）进行矫直计算的关键是建立A C段变形过程中载荷F与挠度δ之间的关系，即求得F＝f（δ）的具体函数表达式。所以矫直过程力学模型的建立问题也就相应转换为了建立弹塑性变形阶段力学模型的问题。以下给出了弹塑性变形过程中力学模型的建立方法，图4为钻杆弹塑性变形阶段相应的变形关系。

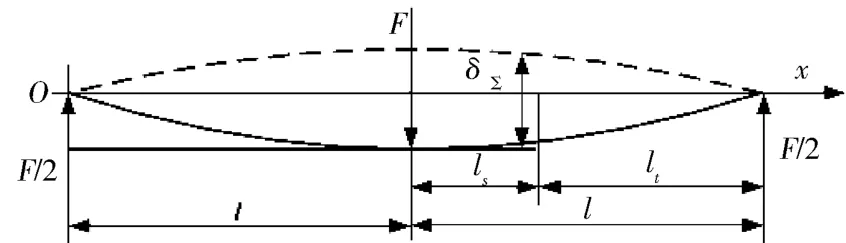
图4 钻杆弹塑性变形阶段关系

1） 弯矩的计算

由图4，钻杆在x轴方向上的弯矩大小可以表示为M＝F x／2，在钻杆弹塑性变形过程中，管段所受弯矩的大小与管材弹区比之间存在着密切的关系，所以钻杆所受弯矩的大小与弹区比之间可表示为M＝f（ζ），当弹区比ξ＝1时，可得到横截面上的极限弹性弯矩：

2） 弹塑性变形阶段矫直压力范围的确定

由M＝F x／2可以确定钻杆施加压力处产生相应弹塑性变形的弯矩范围。在图4所示中点x＝l处，当ξ＝1时，可以得到最小弯矩Mmin，并且由式（9）可知Mmin＝Mt，根据钻杆的材料特性可知，当ξ达到相应允许的最小值时，可以得到最大弯矩Mmax，经计算可以得到相应的压力范围，其函数关系式如下所示［11］：

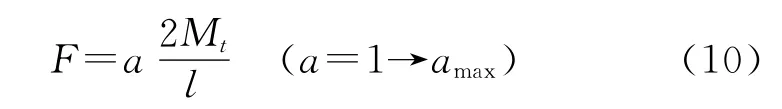
式中：a为压力系数，与工件属性相关，不同工件的a值也不相同。

由式（10）可以得到一个关于a的方程式，其中压力载荷大小的计算与a的取值有关。令a在区间［1，amax］每间隔△a取一值，最后将这些数据综合起来，就可以得到多组工作载荷与矫直挠度的数据，将这些数据在坐标图上按顺序依次连接起来，便可以得到钻杆矫直过程中弹塑性弯曲变形阶段的载荷-挠度曲线图，并且△a取值越小得到的相应曲线就越精确［12］。得出的曲线可由计算机计算得到钻杆矫直过程中所需的各项参数。式（10）除了可以确定矫直载荷以外，因为在弹性变形区与弹塑性变形区的交界处（x＝lt）ξ＝1，所以钻杆变形过程中弹性区的长度为：

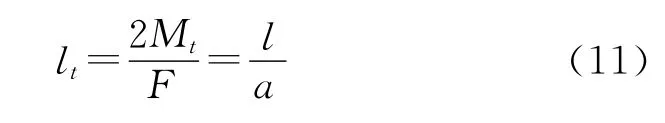
式中：lt为钻杆沿轴线方向弹性变形长度，m。

3） ξ与x关系的确定

由式M＝F x／2和式M＝f（ζ）得到ξ与x之间的关系式：

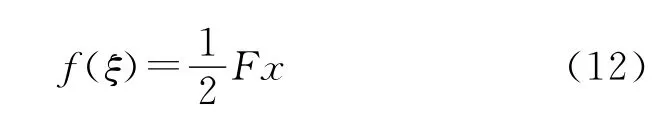
式中：ξ为管材弹区比；x为距支点O的距离。

湖父镇地理位置优越，地处我国苏浙皖三省交界处，交通极为方便。周边有南京、常州、无锡三个机场。宁杭高速、宁杭高铁四通八达。优越的交通条件大大速断了人们自驾游的出行时间。其中上海自驾所需约2小时，杭州约1个半小时，无锡约40分钟。

4） C∑与ξ关系的确定

矫直过程中工件的总曲率与弹区比ξ之间的函数关系式如下：

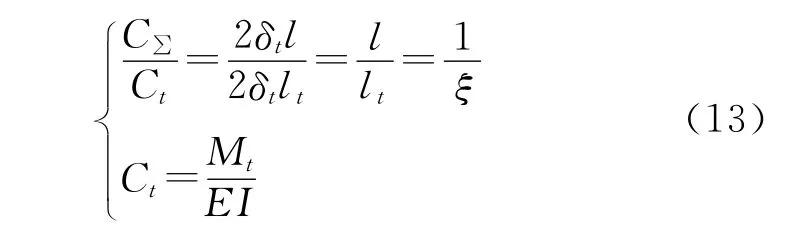
式中：C∑为钻杆由初始弯曲至反弯状态发生的总曲率变化；Ct为钻杆的弹性极限曲率；δt为钻杆达到弹性极限时所对应的应变。

5） 压块的行程（下压量）的确定

联立式（3）和式（4）可以获得C∑与x的关系，可以推导出A C段曲线的函数关系式，也就是相应的弹塑性变形过程中δ的计算公式，函数关系式如下：

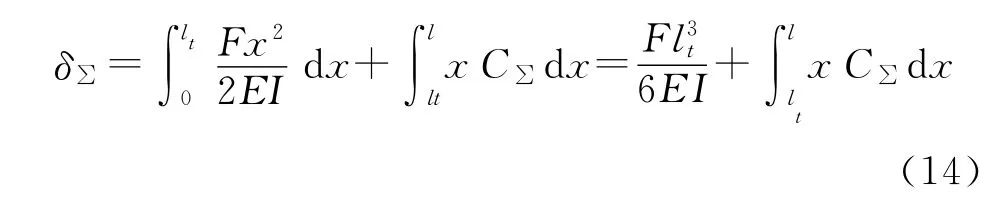
基于前述钻杆矫直假设，其相应的钻杆塑性区及弯矩分布如图5。

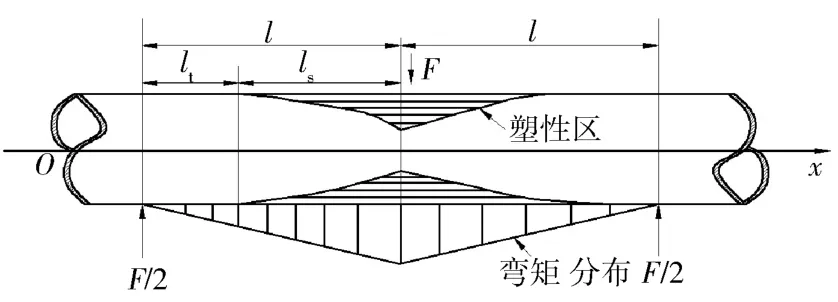
图5 钻杆塑性区及弯矩分布

根据弹塑性变形理论，在弹塑性变形区域内弯矩又可由截面纵向内应力分布积分得到：

外载荷产生的弯矩与内应力产生的弯矩两者应该相平衡，所以联立式（10）和（15）可得：

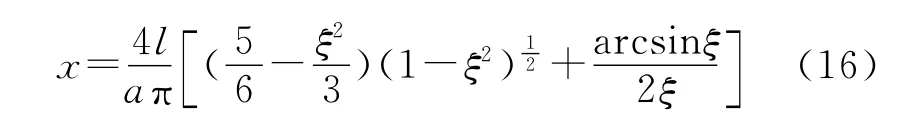
综上，联立各式可以得出整个弹塑性变形阶段力学模型的函数关系式为：

式中：ξ为钻杆弹区比；ls为钻杆沿轴线方向塑形变形长度，m；F为钻杆矫直过程中压力载荷，N；Mt为最大弹性弯矩，N·m；δ∑为钻杆总变形量，m；x为钻杆轴线上任意点位置坐标，m；C∑为钻杆整个弯曲过程的变形曲率。

式（17）反映了整个压力矫直过程中弹塑性变形阶段的函数关系。所以整个矫直过程中的力学模型就可以由式（8）和式（17）予以表示。

2.3 挠度计算

由图3可推导出各参数之间存在如下关系式：

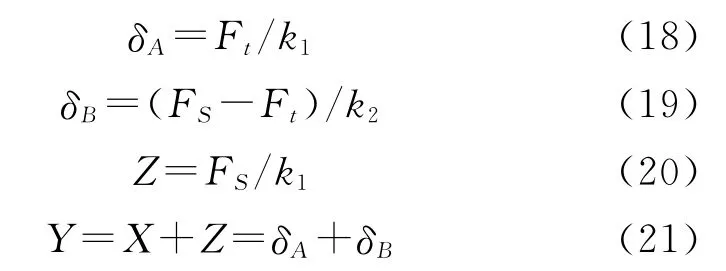
式中：k1表示O A、C D段的斜率；k2表示连接A、C两点的直线段斜率，直线段A C近似代替曲线段A C；Ft为钻杆发生最大弹性变形时所对应的载荷；Fs为塑形变形极限载荷，也是单次矫直过程中所允许施加的最大压力载荷；δA是钻杆在弹性变形阶段产生的最大变形量；δB是钻杆进入弹塑性变形阶段产生的相应的变形量；X为钻杆的初始变形量；Z为钻杆卸载后的弹性回弹量；Y为钻杆矫直过程中总的下压量。

联立上述方程可推导得到如下公式：

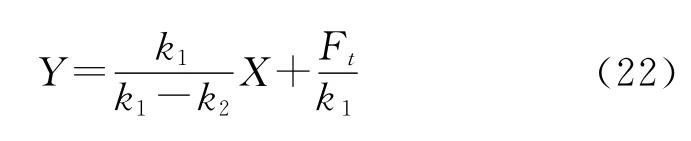
由于O A段为纯弹性变形过程，遵循胡克定律的变形关系，根据简支梁挠度的计算方法可以计算出O A段任意矫直压力F与弹性变形量δt之间的关系为：

式中：δt为钻杆在弹性变形阶段的变形量，m；F为钻杆压下过程中所受的压力，N；I为钻杆截面对中性轴的惯性矩，m4；E为钻杆的弹性模量，Pa。

当两支点的距离确定后，可以得出斜率k1的计算公式为：

由于在弹性变形阶段a＝1，所以由式（17）可以求得弹性变形阶段最大的矫直压力Ft为：

将式（24）和（25）代入式（22）中，可以求出下压量与钻杆初始弯曲量之间的函数关系式为：

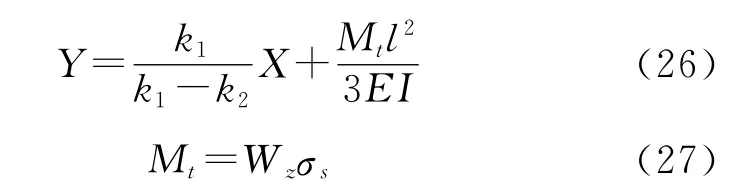
式中：Mt为截面所受最大弹性弯矩，N·m；WZ为钻杆抗弯截面模量，m3；σs为钻杆的屈服强度，Pa。

对于钻杆截面：

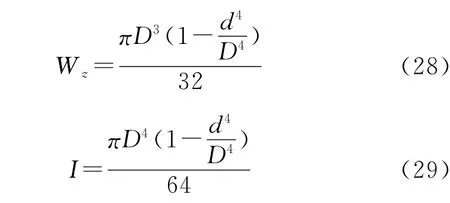
式中：D为钻杆外径，m；d为钻杆内径，m。

将式（27）、（28）代入式（26）中可得：

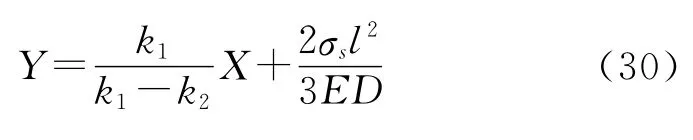
式中：X即为矫直力学模型建立过程中的钻杆初始弯曲量δ0。

故式（31）还可写为：

a0值可以通过计算机对多组实测数据进行线性拟合后予以确定，由此便可以根据钻杆的初始弯曲量δ0依据上述公式来进行矫直过程中下压量的计算。

3 钻杆矫直应力应变分析

利用有限元分析技术可以对钻杆的压力矫直过程进行很好的数值模拟，进而可以对钻杆矫直过程中挠度的变化关系进行有效的分析。

3.1 建立有限元模型

矫直时，钻杆两端由支座支撑，中间部位由压头下压，整个矫直过程可以看作是一个简支梁模型。以内加厚对焊钻杆为例，钻杆公称直径d＝127 m m，内径d1＝109 m m，壁厚h＝9 m m，两支座间距L＝1 000 m m，模型如图6所示。

图6 钻杆压力矫直过程实体模型

钻杆材料特性如表1所示。

表1 钻杆材料参数

采用A N S Y S软件对钻杆矫直进行仿真模拟，以8节点的六面体单元Solid45作为有限元分析的单元类型，对钻杆模型进行网格划分，如图7所示。

图7 钻杆网格划分效果

在进行有限元分析时，钻杆矫直模型实际为一三点反弯力学模型［13］，钻杆两端由支点支撑，中间位置由压头压下。将两支点与中间压头视为刚体，两支点定义为全约束，压点只允许在y方向上移动，随载荷的施加，压头与钻杆表面接触的地方被压扁，从而形成1个接触区域，所以定义施加1个面力。钻杆的弯曲变形相对于支座之间的距离十分微小，分析时忽略钻杆几何形状改变对其材料各项参数的影响。钻杆模型在分析过程中采用的是面与面接触，定义变形体钻杆为接触表面，定义压头和支座的接触面为目标表面，如图8所示。

图8 钻杆接触定义

分别定义加载和卸载2个载荷步，并对每个载荷步划分相应子步，对加载载荷步进行加载并写入载荷步文件，记录加载时的弯曲变形量；再次在原加载处将工作载荷设置为0，相当于卸载并写入载荷步文件，记录卸载后参与变形量。

3.2 仿真结果分析

对钻杆矫直模型施加1组不同的压力载荷F，获得1组相应钻杆弯曲变形量δ，若矫直压力使钻杆发生了弹塑性变形还可以得到钻杆卸载后的残余变形量。将多组这样的数据集合起来，就能够得到相应的压力载荷F与弯曲变形δ之间的关系曲线。

根据A N S Y S软件分析，由于在建立钻杆矫直力学模型时采用了一定的理论假设，为减小由此带来的误差，在式中添加相应的修正系数b0，进而可得到以下公式：

式中：b0为修正系数。（其他在前文中已经提到过）

该模型模拟了钻杆由直管进行压弯后回弹的过程，与实际工作中钻杆由弯曲状态进行加压反弯的过程其基本原理是一致的。通过分析矫直模拟过程中钻杆初始弯曲量与矫直挠度的数据结果，以及对数据结果进行线性拟合可以得到如图9所示的关系曲线。

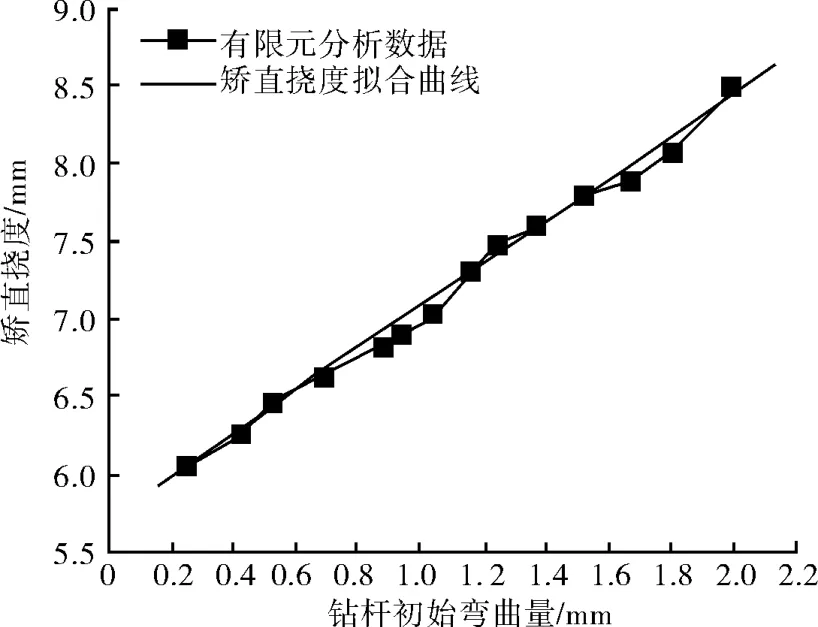
图9 矫直挠度曲线拟合

通过曲线拟合可以得到公式中a0取值一般为1.2～1.4 m m，b0取值一般为0.3～0.6 m m。由此便可以根据钻杆的初始弯曲量δ0，依据上述公式进行矫直过程中矫直挠度的计算。

4 结论

1） 以弹塑性变形理论为基础，结合金属材料弹塑性变形的几何与力学特性建立了钻杆矫直过程中的力学模型，由其可知，下压量与两支座之间的距离、钻杆的屈服强度正相关，与钻杆的外径、钻杆材料的弹性模量负相关。

2） 用A N S Y S软件对钻杆矫直模型进行了应力、应变分析，当工作压力不断增加并且增大到可以使钻杆发生弹塑性弯曲变形时，钻杆矫直过程所对应的挠度值是先呈线形关系变化，进入塑性变形区后挠度值按一定的曲线关系变化，并且卸载后会有残余挠度产生。当钻杆反弯到一定程度后，如果此时矫直压力继续增大，钻杆将发生破坏而无法发生回弹，最终导致钻杆因压弯过量而无法使用。

［1］ 崔甫.矫直原理与矫直机械［M］.北京：冶金工业出版社，2002.

［2］ 袁鹏斌.钻杆弯曲原因分析［J］.技术交流，2010（6）：54-56.

［3］ 崔甫.矫直理论与参数计算［M］.北京：机械工业出版社，1994.

［4］ 张培安，刘邦义，王玉奎，等.钻铤套管和钻杆压力矫直机的设计［J］.石油矿场机械，2005（1）：54-56.

［5］ 曹爱文，熊国良.压力校直技术的发展［J］.锻压装备与制造技术，2007，6（1）：46-55.

［6］ 崔甫.关于弹塑性弯曲的极值问题［J］.重型机械，1991（6）：15-17.

［7］ 崔甫，施东成.矫直机压弯量计算法的探讨［J］.冶金设备，1999，113（1）：1-6.

［8］ 陈慧敏，赖明道.简析圆形断面材料在矫直过程中的弹塑性弯曲变形［J］.焊管，2000，23（3）：66-77.

［9］ 张立玲.管材塑性弯曲回弹量计算［J］.锻压技术，2002，4（3）：37-39.

［10］ 盛艳明.钢轨端部弯曲的压力矫直计算研究［D］.南昌：华东交通大学，2008.

［11］ 李俊，熊国良，皱慧君.轴类零件压力矫直过程的数学模型与行程计算［J］.重型机械，2004（6）：41-44.

［12］ 盛艳明.钢轨端部弯曲的压力矫直计算研究［D］.南昌：华东交通大学，2008.

［13］ 于凤琴.圆钢压力矫直的有限元研究［J］.重型机械，2007（4）：21-22.

M echanical M odel Establish ment and Analysis of Three-point Bending Oil Drill Pipe

G A O Kai
（Drilling Technology Research Institute，Sinopec Shengli Petroleu m Engineering Com pany，Dongying257017，China）

For analyzing the force and deformation of three-point bending oil drill pipes’straightening process，the relationship of bending m o ment，curvature and deflection are explored based on metal elastic-plastic deformation theory，and the mechanical m odel is established to analyze its stress，strain and deflection by using A N S Y S structural analysis software.T he research result indicates that the mechanical m odel can help in quantitative analysis of relationship between stressand physical dimension during the straightening process，im prove the straightening precision and provide theoretical guidance for further designing auto mation oil drill pipe straightening machine.

drill pipe；straightening；mechanical m odel；elastic-plastic deformation

T E921.201

A

10.3969／j.issn.1001-3482.2014.08.007

1001-3482（2014）08-0030-07

2014-03-15

中石化科技项目“动力与信息传输钻杆工程样机研制”（JP13049）

高 凯（1982-），男，山东东营人，工程师，硕士，2012年毕业于中国石油大学（华东）油气井工程专业，现主要从事石油钻采工艺装备研究及科研管理工作，E-mail：gaokai＠sinopec.co m。