激光跟踪系统“鸟巢”坐标的球面标定法

张亚娟，裘祖荣，李杏华，杨 婷

激光跟踪系统“鸟巢”坐标的球面标定法

张亚娟，裘祖荣，李杏华，杨 婷

(天津大学精密测试技术及仪器国家重点实验室，天津 300072)

深入分析了激光跟踪测量系统坐标系的特点，建立了采用高精度约束球面标定激光跟踪测量系统(LTS)的初始状态参量和结构误差参量的方法．通过数学仿真搜索出采用约束球面进行系统标定时的最佳约束球半径、最佳采样点个数等，并采用仿真方法评估系统噪声对标定结果的影响．使用三坐标测量机和QC20-W高精度伸缩球杆仪建立了球面约束标定的实验装置，对激光跟踪系统执行了球面约束标定实验．实验结果表明，采用高精度约束球面作为约束条件可以提高系统的未知参数标定精度和测量精度．

激光跟踪系统；标定；数学模型；约束球面；坐标测量

激光跟踪系统(laser tracking system，LTS)是在机器人计量学领域发展出的三坐标测量设备[1-2].“鸟巢”是激光跟踪系统上的一个固定点，测量前需要标定出“鸟巢”到坐标原点的距离Lr．Lr称作“鸟巢”的坐标，其标定精度直接影响系统的测量精度．同时，影响跟踪系统测量精度的重要因素还有机械结构误差中的两回转轴线的位置误差、跟踪转镜的安装误差和入射光束的对准误差[3-4]．美国佛罗里达大学的Shui Hu Motaghedi曾为跟踪系统建立了包含“鸟巢”坐标和上述误差源在内的动态数学模型，并设计了约束平面法来求解“鸟巢”坐标和各误差参数的值．实验证明，该动态模型可以在一定程度上消除系统结构误差影响，提高测量精度．但是，由于高精度的约束平面难以获得，且以平面为约束条件的约束方程的误差传递系数大，因此标定方案实施难度大，标定精度难以得到保证[5-7]．

笔者以Shui Hu Motaghedi建立的跟踪系统动态模型为基础，研究以高精度球面约束取代平面约束对“鸟巢”坐标和结构误差等进行标定的理论和实验方法．用约束球面取代约束平面是因为目前的标准球精度很高，球度误差往往控制在几十纳米．利用球轴承的高精度伸缩靶模拟运行球面的球面度也能够控制在两三个微米内．高精度的约束球面比高精度的约束平面易于加工和获得，因此，采用球面约束有望提高标定精度．

1 激光跟踪系统的动态数学模型

图1为初始状态下激光跟踪系统的示意，主要由跟踪头和目标靶镜组成．其中，跟踪头的主要结构是轴线(R1和R2)垂直相交的两回转轴．在回转轴线的交点处安装一平面反射镜，称为跟踪转镜．在两回转轴带动下，跟踪转镜可将入射在其上的激光束始终反射到目标靶镜处．目标靶镜接收激光束并将其反射回去，与系统中的参考光束相干涉．当目标靶镜位置发生变化时，通过干涉信息便可得到目标靶镜当前位置与上一位置相对于坐标系原点O的距离的变化量，记作lm．同时，与回转轴同轴安装的测角装置可以测量出目标靶镜的当前点相对于上一点的偏摆角和俯仰角的角度变化量，分别记作θ1和θ2．系统中有一个固定点，称作“鸟巢”，它是目标靶镜的初始位置，图1中目标靶镜恰好处于“鸟巢”中．“鸟巢”与系统坐标系原点O的距离记为Lr．

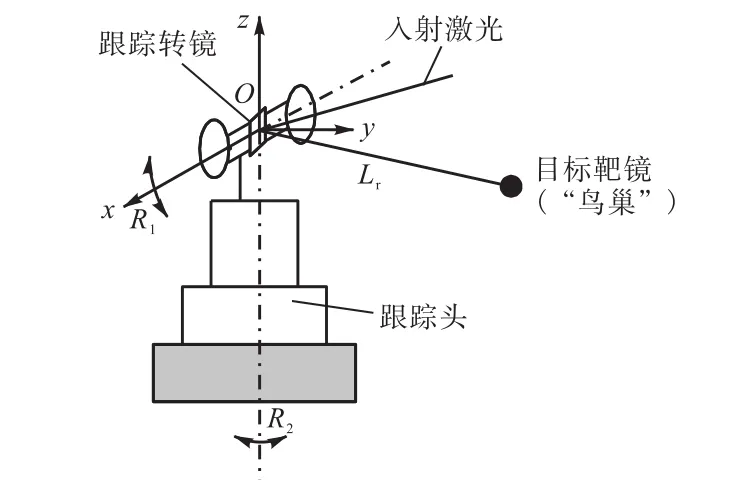
图1 激光跟踪系统示意Fig.1 Schematic of LTS

Lr是需要标定求解的一个系统未知参数，其标定精度直接影响着系统的测量精度．同时，影响系统测量精度的重要因素还包括机械结构误差中的两回转轴线的位置误差、跟踪转镜的安装误差和入射光束的对准误差．当不考虑这些误差时，系统的理想光路如图2所示．其中{xb，yb，zb}、{x1，y1，z1}和{xm，ym，zm}分别是为了分析方便而建立的系统的测量坐标系、辅助坐标系和镜面坐标系．bI、bc、bo分别是入射激光束、镜面法线向量和出射激光束．此时，空间任一点P在系统坐标系中坐标的向量表示为

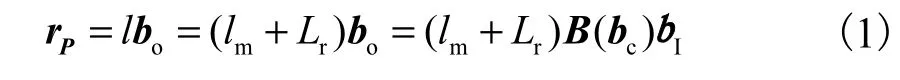
其中

bI可由入射光束在系统坐标系中的两个方位角αI和βI的三角函数向量来表示．

图2 激光跟踪系统理想光路示意Fig.2 Schematic of ideal light path of LTS

当考虑两回转轴线的位置误差、跟踪转镜的安装误差和入射光束的对准误差时，系统的光路如图3所示．

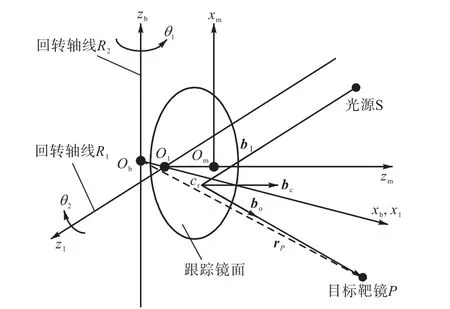
图3 跟踪系统光路示意Fig.3 Schematic light path of LTS

此时，空间任一点P在系统坐标系中坐标的向量表示为

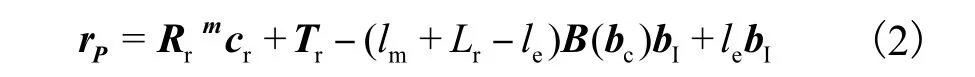
其中

式中：Rr和Tr分别为θ1=θ2=0时坐标系{xb，yb，zb}和{xm，ym，zm}之间的旋转矩阵和平移矩阵，它们的表达式中包含了代表两回转轴线位置误差和跟踪转镜安装误差的5个误差参数α1、e1、α2、β2和e2，其中α1为两回转轴线的真实夹角，e1为两回转轴线的距离，α2为跟踪转镜安装角度误差1，β2为跟踪转镜安装角度误差2，e2为跟踪转镜与回转轴线R1的不重合度；cx，cy为θ1=θ2=0时光线对准偏差的两个参数，cx为激光入射点在转镜坐标系下的x坐标，cy为激光入射点在转镜坐标系下的y坐标．

式(2)是激光跟踪测量系统的动态数学模型．式(1)和式(2)的详细推导过程参见文献[5]．

用V表示由数学模型(2)中未知参数组成的向量，即V=[αI，βI，Lr，cx，cy，α1，e1，α2，β2，e2]T．

由于V中的各参数值均是目标靶镜处于“鸟巢”时的系统状态参量，因此，将向量V形象地称为跟踪系统的“鸟巢”坐标．对V的求解，称为对“鸟巢”坐标的标定．

当跟踪仪的机械结构为理想情况时，“鸟巢”坐标V中的各元素值分别为cx=0，cy=0，α1=90°，α2=90°，β2=90°，e1=0，e2=0．

2 球面约束标定原理

如图4所示，将一个标准球放在跟踪系统测量空间的任意位置，设球心C在跟踪仪测量坐标系中的坐标为[Ls，αs，βs]T，球面半径为R．

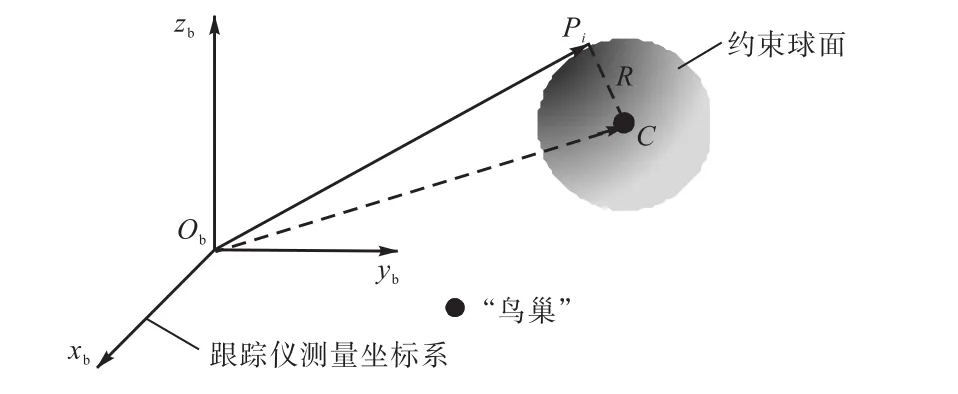
图4 球面约束标定法示意Fig.4 Spherical constraint calibration method

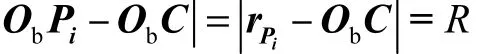
对球面上每一个点Pi均有

对于球面上n个测量点可建立n个上述方程，由这n个方程可建立如下目标函数：

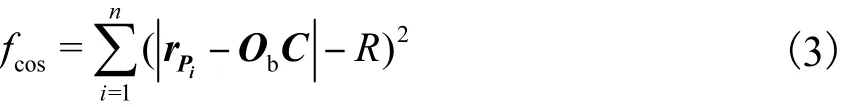
当测量点数n大于式(3)中未知数个数时，用最小二乘法即可求得所有未知数的值，从而实现对跟踪系统动态数学模型中“鸟巢”坐标V的标定．

在采用球面作为约束进行标定时，约束球面的半径R有两种处理方法：一是将其作为已知参数，此时未知参数向量变为[V，Ls，αs，βs]T；二是将其作为未知参数，这样则无需事先测量标准球的半径，标准球的半径通过标定获得，此时未知参数向量为[V，Ls，αs，βs，R]T．在后面的仿真和实验中，将半径R作为未知量处理．

3 标定法仿真

在设计球面约束标定法的实验装置和进行标定实验之前，首先对该方法的可行性进行理论分析，分析主要包括4个方面．

(1) 最小二乘法求解过程的收敛性．若最小二乘法求解未知数的迭代算法无法收敛，则该方法不可行．

(3) 标定时的最佳采样点数分析．确定标定的最佳采样点数既可以保证顺利求得各未知参数，又可以避免由于采样点过多而增加标定工作的强度．

(4) 约束球面半径取值对标定精度影响分析．约束球面半径取值对于球面约束方法的可行性具有重要意义．如果为了达到所需的标定结果而需要约束球具有很大的半径以至于无法创建真实的实验环境，则球面约束法虽理论上可行，但仍不能实现真正的标定．只有当约束球面的半径取值在一个合理的范围内时，该方法才具有实际的应用价值．

理论分析采用Matlab仿真方法模拟标定过程，并分析以上各因素对标定结果的影响．

仿真时，设各未知参量的真实值如表1所示．

表1 仿真参数的真实值Tab.1 Real values of the parameters

跟踪仪系统中“鸟巢”距坐标原点的距离Lr一般为0.20～0.35,m，因此仿真中取Lr=0.35,m．当采用精密工具对入射光进行调整时，其入射精度能够高达0.1,mm．通过加工过程中控制两回转轴线的相互位置偏差，可使α1和e1分别控制在90.01°和0.01,mm．由于镜面安装精度比两回转轴线的形位精度难以控制，因此其安装误差分别设为90.02°和0.02,mm．

假设跟踪系统可以测到约束球面上的任意一点．在仿真时，首先用Matlab在球面上取足够数量的采样点，分别计算各采样点的“测量值”lm、θ1和θ2，然后建立式(2)所示的约束方程，采用Lervenberg-Marquadt方法求解最小二乘问题，可得到未知向量[V，Ls，αs，βs，R]T的解．

在实际系统中，噪声会影响标定精度．为使仿真更接近实际情况，分别给仿真数据添加表2所示的噪声值，其中U代表均匀分布的噪声．

未来海域常规油气产量浅水保持稳定，深水和超深水逐渐发力。中东、亚太及非洲地区产量增长较明显，欧洲地区在高峰产量后递减明显。

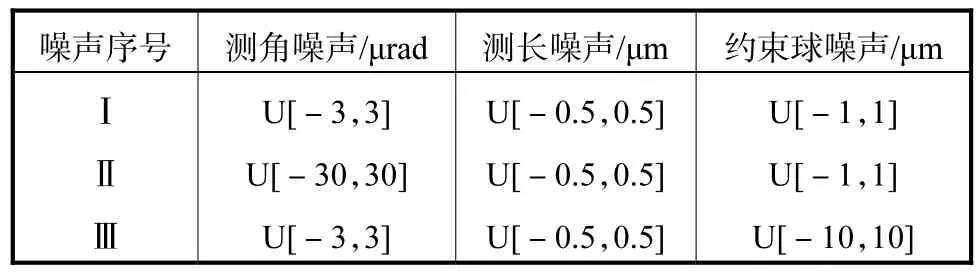
表2 加在仿真测量值上的平均分布的误差Tab.2 Measurement noises added to simulation data

系统中使用的测角圆光栅，其角度测量不确定度的范围大约为0.7″～6.3″，相应的弧度值约为3～30,μrad．双频激光干涉仪的测长不确定度一般在几十纳米，由于温度、湿度等环境因素的影响，其测量精度有可能下降，在稳定的实验室条件下，影响双频激光干涉仪测量精度的气象因素较小，因此双频激光干涉测距系统的测量不确定度取为±0.5,μm是合理的．高精度标准球的球度误差一般在几十纳米，用磁性球靶模拟出的球面的球度误差大约在两三个微米．因此，为了进行对比，分别给出1,μm和10,μm两个不同级别的球度误差．球度和球面粗糙度误差被加在采样点的坐标中．这些误差包含了其他非几何因素的误差，如由温度和湿度引起的测量误差等．

为了表示在不同情况下标定结果的优劣，在每次采点时，另外采10个点作为检测点．系统参数标定结束后，用系统的动态测量模型去“测量”10个采样点的坐标，并与其真实坐标进行对比．将理想点与测量点之间的距离作为衡量标定结果优劣的标准，记为E[8-9]．

仿真结果表明，球面约束标定算法具有很好的收敛性，能够精确地求出系统各未知参数的值．

图5所示为仿真时测点数目、约束球半径、系统噪声等与E的关系．

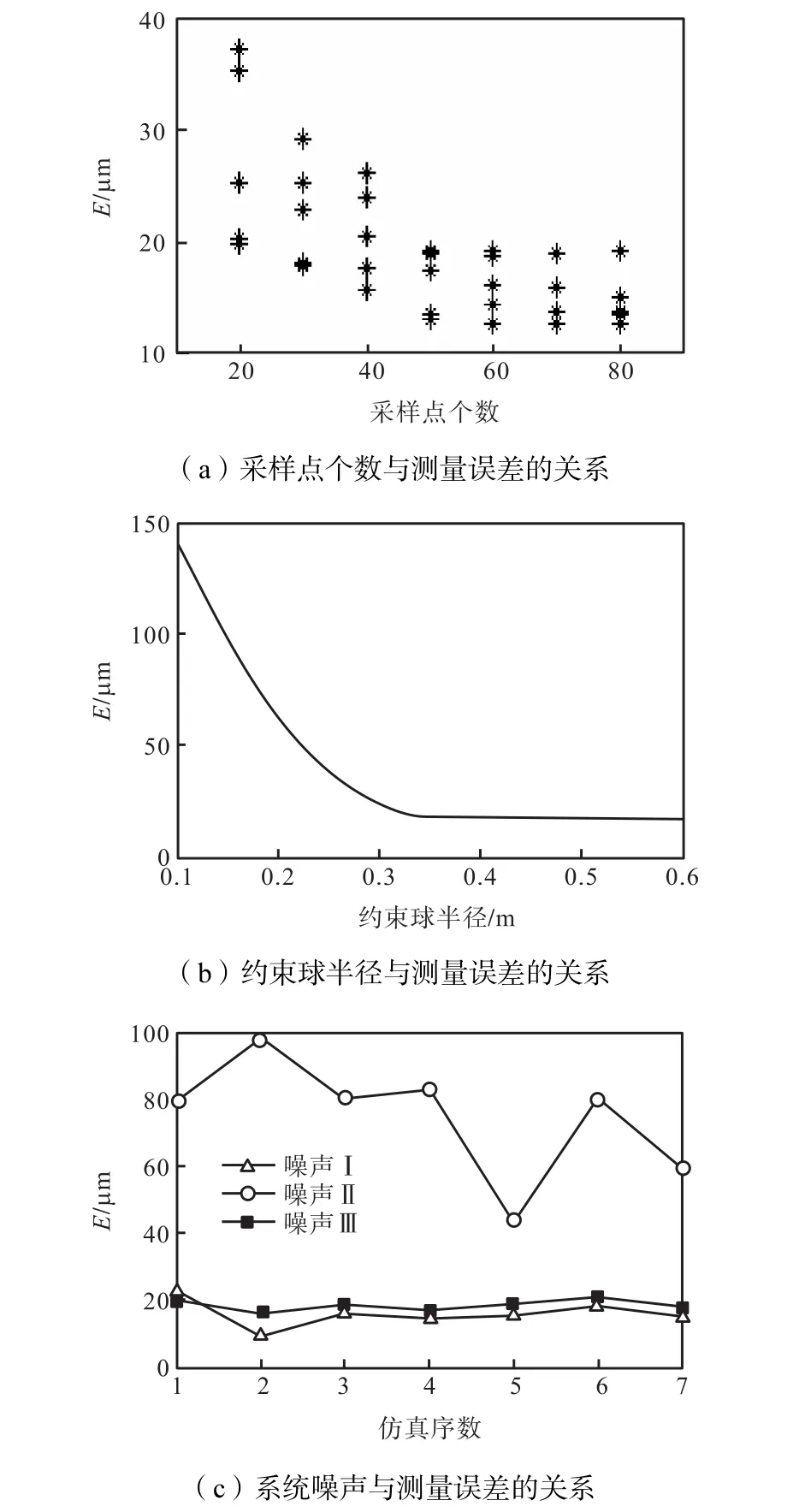
图5 仿真的测量误差Fig.5 Measurement error of simulation

仿真时分别采取不同的采样点数，各进行5次仿真．由图5(a)可见，当采样点数大于或等于50个时，测量误差趋于稳定．因此，采用球面约束进行标定时，采样点数不能少于50个．用各种半径的约束球各进行5次仿真并将5次仿真结果取平均值．由图5(b)可见，当约束球半径大于等于0.35,m时，测量误差趋于稳定．因此，采用球面约束时约束球的半径应大于或等于0.35,m．图5(c)中显示的是添加不同噪声时的测量误差．噪声Ⅱ误差明显大于噪声Ⅰ，说明当存在较大的角度测量误差时，标定后系统的测量误差也较大．该仿真结果从一个侧面印证了单站式激光跟踪坐标测量系统的测角误差为其测量误差的一个主要来源[7]．噪声Ⅰ、噪声Ⅲ两组数据比较，当球度误差增大时，标定后的测量误差也相应地有所增大，但是其增加幅度并不十分明显，说明球面约束标定激光跟踪系统时球面的球度噪声对标定精度影响较小．

以上仿真结果证明，采用球面约束法标定激光跟踪系统“鸟巢”坐标的方法是可行的．标定时最佳采样点数为50，约束球半径不得小于0.35,m．

4 实 验

为了验证球面约束法标定激光跟踪系统的实际效果，需要为标定方法设计可行的实验装置．而设计实验装置的关键点就是建立半径大于等于0.35,m的高精度约束球面，并使跟踪仪的目标靶镜能够在约束球面上采点．经过研究，本文将三坐标测量机和Renishaw的QC20-W球杆仪组合使用完成了实验平台的设计．整体标定实验装置如图6所示．

将球杆仪的基座固定在三坐标测量机的实验平台上，球杆仪的一端吸附在支座的带磁性的支撑座上，另一端吸附在安装于三坐标测量机上的磁性支座上[10]．同时将激光跟踪系统的目标靶镜牢固地安装在三坐标测量机上．编写三坐标测量机控制程序，使三坐标测量机带动球杆仪的一端以另一端的支撑中心为球心在球面上连续运动．这样，当球杆仪的一端沿着球面运动时，跟踪系统的目标靶镜也沿着一个同样半径的球面运动，只是这两个球的球心位置不同．由于三坐标测量机的运动误差较大，球杆仪运动端所形成的球面“粗糙度”很大．但是球杆仪内部的高精度位移传感器能够感知每一个测量点与初始点相比的半径变化量．设初始位置时球杆的长度为Lg，那么其他各测量点处的半径为

式中：li为每个采样点的球面半径；Si为球杆仪位移传感器的读数．对每个采样点均有=Lg+Si．

最小二乘算法求解时的约束方程相应地调整为

式(4)即为采用球面约束法进行激光跟踪系统标定实验时所采用的约束方程．

系统中所用球杆仪的位移传感器分辨力为0.1,μm，传感器的测量精度为±0.5,μm，球杆仪系统的测量精度为1.25,μm，测量范围为1,mm．球杆采用加长杆，将长度加长为0.35,m．

在该系统中对本实验室研制的单站式激光跟踪系统(见图7)进行了球面约束标定，标定结果收敛．

图7 激光跟踪系统Fig.7 Laser tracking system

为了检验球面约束标定法的实验效果，同时对系统进行了平面约束标定．平面约束标定的具体原理和方法参见文献[5]．

然后用两种标定方法标定出的系统分别测量空间中位于同一条直线上的多条线段长度，同时用HP5519双频激光干涉仪也测量这些线段的长度(见图8)．以双频激光干涉仪的测量结果作为标准，将跟踪仪的测量结果与干涉仪的测量结果进行比较，误差越小说明测量结果越精确，标定效果越好，反之说明标定效果越差[8]．两种标定方法对跟踪仪未知参数的标定结果见表3．线段长度测量结果见表4．

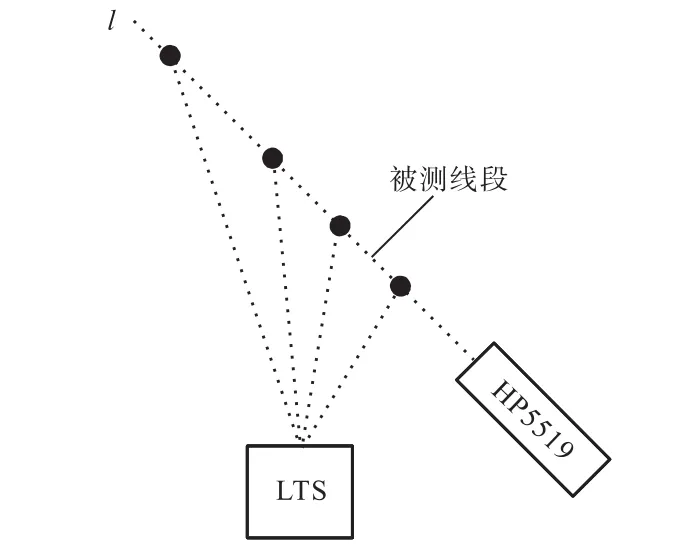
图8 对比实验装置示意Fig.8 Contrast experiment setup

表3 标定结果Tab.3 Calibration results

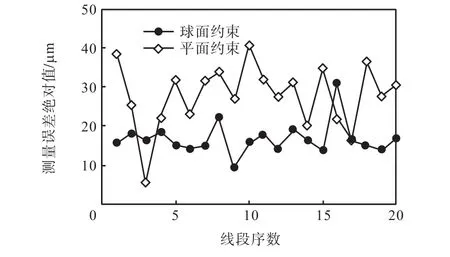
图9 系统测量误差示意Fig.9 System measurement error

表4 对比实验结果Tab.4 Comparison of experimental results

图9所示为两种方法标定后的系统对直线上线段的测量值与双频激光干涉仪测量值差的绝对值.横坐标代表所测线段的序数，纵坐标代表测量误差绝对值．由图9可见，采用球面标定后的系统的测量误差比采用平面约束标定的系统的测量误差显著降低．经计算，采用球面约束标定后对20条线段测量误差的均值为16.7,μm，而采用平面约束的测量误差的均值为27.9,μm．误差均值减小了40.1%．

5 结 语

本文提出了采用高精度球面作为约束条件标定激光跟踪系统动态模型中“鸟巢”坐标的原理．验证了该原理的可行性并设计了由三坐标测量机和Renishaw的QC20-W球杆组成的标定实验系统．实现了对激光跟踪系统“鸟巢”坐标的标定，提高了系统的标定精度和测量精度．

为了进一步提高标定精度，可以分别从提高约束元素本身的精度和降低算法的误差传递系数上考虑．由双频激光干涉仪提供的约束直线具有很高的几何精度．但是研究中发现，采用直线约束的数学算法的误差传递系数较平面约束和球面约束要大很多，很可能导致求解失败．因此若要取得好的标定效果，需要对直线标定法研究更好的求解非线性方程组的数学算法．

［1］ 陈晓荣，陈淑芬. 球坐标法激光跟踪测量系统自校正方法研究[J]. 中国机械工程，2006，17(增)：133-134，139.

Chen Xiaorong，Chen Shufen. Research on selfcalibration of laser tracking measurement system [J]. China Mechanical Engineering，2006，17(Suppl)：133-134，139(in Chinese).

［2］ Carl-Thomas Schneider. Laser tracer—A new type of self tracking laser interferometer[C]//Proc IWAA2004. Geneva，Switzerland：CERN，2004：1-6.

［3］ Jiang Hong，Osawa Sonko，Takatsuji Toshiyuki，et al. High-performance laser tracker using an articulating mirror for the calibration of coordinate measuring machine[J]. Optical Engineering，2002，41(3)：632-637.

［4］ Takatsuji Toshiyuki，Koseki Yoshihiko，Goto Mitsuo，et al. Laser-tracking interferometer system based on trilateration and a restriction on the position of its laser trackers[C]// Proc SPIE，Laser Interferometry IX：Applications. San Diego，CA，1998，3479：319-326.

［5］ Shui Hu Motaghedi. Self Calibration of Laser Tracking Measurement System with Planer Constraint[D]. Florida：College of Engineering，Florida Atlantic University，1999.

［6］ Zhuang Hanqi，Motaghedi S H，Roth Z S，et al. Calibration of multi-beam laser tracking systems[J]. Robotics and Computer-Integrated Manufacturing，2003，19(4)：301-314.

［7］ Umetsu Kenta，Furutnani1 Ryosyu，Osawa Sonko，et al. Geometric calibration of a coordinate measuring ma chine using a laser tracking system[J]. Meas Sci Technol，2005，16(12)：2466-2472.

［8］ 林永兵，张国雄，李 真，等. 四路激光跟踪干涉三维坐标测量系统自标定与仿真[J]. 仪器仪表学报，2003，24(2)：205-210.

Lin Yongbing，Zhang Guoxiong，Li Zhen，et al. Selfcalibration and simulation of the four-beam laser tracking interferometer system for 3D coordinate measurement[J]. Chinese Journal of Scientific Instrument，2003，24(2)：205-210(in Chinese).

［9］ 刘万里，王占奎，曲兴华，等. 激光跟踪测量系统跟踪转镜的误差分析[J]. 光学 精密工程，2008，16(4)：585-589.

Liu Wanli，Wang Zhankui，Qu Xinghua，et al. Error analysis of tracking mirror for laser tracker system[J]. Optics and Precision Engineering，2008，16(4)：585-589(in Chinese).

［10］ 王东升，李书和，张国雄. 用Renishaw检查规进行三坐标测量机几何误差检测的研究[J]. 仪器仪表学报，1999，20(4)：389-391.

Wang Dongsheng，Li Shuhe，Zhang Guoxiong. Measurement of geometric errors of CMM with Renishaw checking gauge[J]. Chinese Journal of Scientific Instrument，1999，20(4)：389-391(in Chinese).

(责任编辑：赵艳静)

Calibration of Laser Tracking System with Spherical Constraint

Zhang Yajuan，Qiu Zurong，Li Xinghua，Yang Ting
(State Key Laboratory of Precision Measuring Technology and Instruments，Tianjin University，Tianjin 300072，China)

Coordinate system characteristics of the laser tracking system(LTS)are analysed，and a method using sphere as constraint to calibrate the initial state parameters and structure error parameters of LTS is provided. Through Matlab simulation，the optimal number of sample points，optimal radius of sphere for system calibration are obtained，out and the impact of system noises on the calibration results is assessed. An experimental apparatus for spherical calibration is established by using CMM and QC20-W ball bar，and experiments are carried out on this system. The results show that this method can improve the accuracy of unknown parameters and the measurement accuracy of the system.

laser tracking system；calibration；mathematical model；spherical constraint；coordinates measurement

TH741

A

0493-2137(2014)03-0255-07

10.11784/tdxbz201204049

2012-04-30；

2012-09-30.

张亚娟（1984— ），女，博士研究生，yajuanzhang216@163.com.

裘祖荣，qzr@tju.edu.cn.